матан. заочники матем 1 семестр по вариантам. Программа, методические указания и контрольные задания 1 семестра для студентов заочной формы обучения всех специальностей
 Скачать 374.69 Kb. Скачать 374.69 Kb.
|
Задание 3.4.Провести полное исследование функции с помощью производных первого и второго порядков. По результатам исследования построить графики функций. а) y x3  x2 4 ; x2 4 ;б) y ln x.  Решение. Решение.а) Исследуем первую функцию. Область определения функции дроби не может быть равен нулю. D(x) Проверяем четность (нечетность функции): (x)3 x3 y(x) (x)2 4 x2 4 y(x). Следовательно, функция является нечетной (ее график симметричен относительно начала координат). Функция не является периодической, т.к. является отношением двух элементарных не периодических функций. Находим асимптоты. Из области определения имеем точку разрыва x3 x 2, причем  lim limx2 x2 4 , следовательно, x 2 является вертикальной асимптотой графика функции. В силу нечетности функции вертикальной асимптотой. Ищем наклонную асимптоту y kx b : x 2 так же является y x3 x2 : x2 1 k lim x x lim x x(x2 4) lim x (x 2 4) : x2 lim  x 1 4 x 1 4 1; x2 x3 x3 x(x2 4) 4x : x2 b lim y kx lim 2 4 x  lim x2 4 lim   x2 4 : x2 x2 4 : x2x  lim 4 x lim 4 xx x 0. x x x 1 4 x2 Уравнение наклонной асимптоты: y x . Находим экстремумы функции и интервалы возрастания и убывания: 3 y x 3x2 x2 4 x3 2x  2 2  x4 12x2  2 2x2 x2 12 2 ;  x 4 x2 4 x2 4 x2 4 y 0 при x 0, x 2 3; при x 2 y не существует.  Найденные точки разбивают область определения функции на промежутки монотонности. Определим знак производной и в зависимости от него возрастание или убывание функции. Результаты исследования представим в виде таблицы (в силу нечетности функции достаточно рассмотреть только область при х 0 ). Найденные точки разбивают область определения функции на промежутки монотонности. Определим знак производной и в зависимости от него возрастание или убывание функции. Результаты исследования представим в виде таблицы (в силу нечетности функции достаточно рассмотреть только область при х 0 ).
x 0 не является экстремумом, т.к. при переходе через нее производная не меняет знак. Находим интервалы выпуклости и вогнутости графика функции и точки перегиба: 3 2 2 4 2 2 x4 12x2 4x 24xx 4 x 12x 2x 4 2x y   x2 42 x2 44 4x3 24xx2 4 x4 12x2 4x  x2 43 4x x2 6x2 4 x4 12x2  ; x2 43 4x x4 4x2 6x2 24 x4 12x2  x2 43 4x 2x2 24  x2 43 8x x2 12  x2 43 y 0 при x 0; при x 2 y не существует. Найденные точки разбивают область определения функции на интервалы выпуклости и вогнутости. Определим знак второй производной и в зависимости от него поведение функции. Результаты исследования представим в виде таблицы (в силу нечетности функции достаточно рассмотреть только область при х 0 ).
Точка x 0 является точкой перегиба, т.к. при переходе через нее вторая производная меняет знак, точка x 2 не является точкой перегиба, т.к. она не входит в область определения функции. Находим точки пересечения графика с осями координат. Точка пересечения графика с осью Оу была найдена при исследовании функции на экстремум. Для определения точек пересечения с осью Ох решаем уравнение: у 0,  x3 x3т. е. x2 4 0 . Единственное решение уравнения: x 0 . Значит, график пересекает оси координат только в начальной точке (0, 0). Используя полученные данные, строим график функции при отражаем его симметрично относительно начала координат (рис. 5). х 0 , затем  x3 Рисунок 5. График функции y x2 4 б) Исследуем вторую функцию. 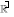 Область определения функции D(x) или Область определения функции D(x) илиD(x) (0; ), т. к. логарифм и подкоренное выражение, стоящее в знаменателе, существуют только при положительных значениях аргумента. Функция не является четной или нечетной (следует из области определения), т. е. имеем функцию общего вида. Функция не является периодической, т. к. является отношением двух элементарных не периодических функций. Находим асимптоты. Из области определения имеем точку разрыва x 0 , причем lim lnx , следовательно, x 0 является вертикальной 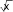 x0 x0 0 асимптотой графика функции. Ищем невертикальную (правостороннюю) асимптоту только при х : k lim y lim  ln x lim ln x /используемправило Лопиталя/  x x  1 1x x lim   х х lim 2 0;  x 3 х1 2 x 3 х1 2 2 x 3х3 2 b lim x y kx 1 lim x ln x /используемправило Лопиталя/ 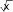 lim x 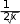 х х lim x x lim 2 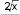 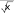 x x 0; Получаем уравнение правосторонней горизонтальной асимптоты (т. к. угловой коэффициент k 0 при х ): y 0 . Находим экстремумы функции и интервалы возрастания и убывания: 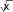 1 ln x 1 1 ln x 1 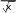  y ln x x y ln x x 2 x 2 ln x 2 ln x; 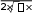  x xy 0 при x e2, y существует только при x 0 . Определим интервалы монотонности и экстремум функции с помощью таблицы:
 Находим интервалы выпуклости и вогнутости графика функции и точки перегиба: Находим интервалы выпуклости и вогнутости графика функции и точки перегиба:  1 x3 2 2 ln x 3 x1 2 1 x3 2 2 ln x 3 x1 2y 2 ln x 1 2 ln x  1 x 2    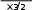 2 2 x3 2 2 x3 1 2    3 1 2   x1 2 1 x 2 ln x x  2 2 1 2 2 2 ln x 3 263lnx 3lnx8  2 x3 2 x3 4x5 2 4x5 2 ; y 0 при x e8 3; y существует только при x 0 .     Определим интервалы выпуклости и вогнутости графика функции, а также точку перегиба с помощью таблицы: Определим интервалы выпуклости и вогнутости графика функции, а также точку перегиба с помощью таблицы:
  Находим точки пересечения графика с осями координат: Находим точки пересечения графика с осями координат:График не пересекает ось Оу, т.к. точка x 0 не принадлежит области определения функции (ось Оу является вертикальной асимптотой). Находим пересечение с осью Ох: у 0, т.е. ln x 0 . Единственное  решение уравнения: решение уравнения:x 1. Получаем точку пересечения (1;0).  По результатам исследования строим график функции (рис. 6). По результатам исследования строим график функции (рис. 6).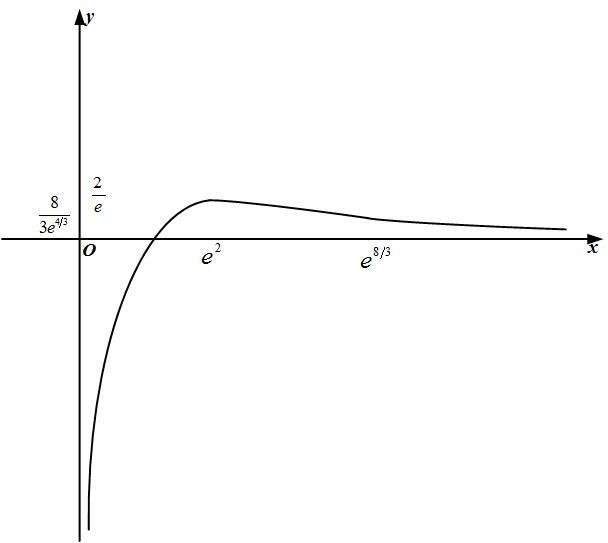 Рисунок 6 График функции y ln x |
