Математика. Математика - примерная рабочая программа (технологический профил. Рабочая программа общеобразовательной учебной дисциплины Математика (углубленный уровень)

• Название: Рабочая программа общеобразовательной учебной дисциплины Математика (углубленный уровень)
• Анкор: Математика
• Дата: 10.01.2023
• Размер: 1.2 Mb.
• Имя файла: Математика - примерная рабочая программа (технологический профил.docx
• Тип: Примерная рабочая программа; #879149
• страница: 7 из 10

Фонды оценочных средств по специальности 11.02.16 Монтаж, техническое обслуживание и ремонт электронных приборов и устройств.

Фонды оценочных средств (далее – ФОС) представлены в виде междисциплинарных заданий, направленные на контроль качества и управление процессами достижения ЛР, МР и ПР, а также создание условий для формирования ОК и (или) ПК у обучающихся посредством промежуточной аттестации. ФОС разрабатываются с опорой на синхронизированные образовательные результаты, с учетом профиля обучения, уровня освоения общеобразовательной дисциплины «Математика» и профессиональной направленности образовательной программы по специальности 11.02.16 Монтаж, техническое обслуживание и ремонт электронных приборов и устройств.

Таблица 6

№ раздела, темы	Коды образовательных результатов (ЛР, МТР, ПР, ОК, ПК)	Варианты междисциплинарных заданий
Раздел № 1 Повторение курса математики основной школы Тема Решение систем уравнений методом Гаусса	ПРу 2 ЛР 13 МР 9 ОК 01 ОК 02 ОК 03 ОК 04 ПК 1.1.	Задание 1. При расчете сложной цепи постоянного тока получилась следующая система уравнений: 7,5 I1 +2 I2 + 5 I3 = 100 2 I1 +12.5 I3 -10 I3 = 120 5 I1 – 10 I2 +25 I3 =0 Решите данную систему методом Гаусса.
Тема Комплексные числа	ПРу 2 ЛР 13 МР 9 ОК 01 ОК 02 ОК 03 ОК 04 ПК 1.1.	Задание 1. По закону Ома вычислите комплексный ток в цепи:
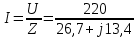
Раздел № 3 Показательная функция Тема Показательные уравнения	ПРб 4 ПРб 8 ПРу 2 ЛР 13 МР 5 МР 9 ОК 01 ОК 02, ОК 03 ОК 04 ОК 09 ПК 1.1.	Задание 1. Найти наибольший положительный корень уравнения ex - 10 x = 0 с точностью 10-4, используя метод итераций. Корни отделить графически. Рассмотреть простейшее решение в системе MathCad.
Раздел № 4 Логарифмы Тема Логарифмические уравнения	ПРб 8 ПРу 2 ЛР 13 МР 5 МР 9 ОК 01 ОК 02, ОК 03 ОК 04 ОК 09 ПК 1.1.	Задание 1. Найти наибольший положительный корень уравнения 4 x - 5 ln x = 5 с точностью 10-4, используя метод итераций. Корни отделить графически. Рассмотреть простейшее решение в системе MathCad.
Раздел 8. Начала математического анализа. Тема Физический смыл производной	ПРу 4 ЛР 13 МР 3 МР 9 ОК 01 ОК 02 ОК 03 ОК 04 ОК 09 ПК 1.1.	Задание 1. Количество электричества, протекающее через проводник, начиная с момента времени t = 0, задается формулой Q = 3t2 – 3t + 4. Определить силу тока в конце 6-й секунды.
Тема Определённый интеграл. Задачи практического содержания	ПРу 4 ЛР 13, МР 3 МР 9 ОК 01 ОК 02 ОК 03 ОК 04 ОК 09 ПК 1.1.	Задание 1. Сила тока в проводнике меняется со временем по закону I=2+3t2. Определить, какое количество электричества проходит через поперечное сечение проводника за время от 2 до 5 секунд.
Раздел 9. Комбинаторика, статистика и теория вероятностей Тема Математическая статистика	ПРу 5 ЛР 13 МР 3 МР 9 ОК 01 ОК 02 ОК 03 ОК 04 ОК 09 ПК 3.3.	Задание 1. При индивидуальном анкетном опросе группа из пяти экспертов в результате генерации подала 26 предложений, относящихся к объекту экспертизы, некоторые из которых по содержанию совпадают друг с другом. При этом n5(5)=10 предложений выдвинуты всеми экспертами (очевидные); n5(4)+n5(3)=4+3=7 предложений выдвинуты большинством экспертов, но не всеми, в данном случае тремя и четырьмя (известные); n5(2)=6 предложений выдвинуты меньшинством, в данном случае, двумя экспертами (неочевидные) и n5(1)=3 предложения выдвинуты (каждое) лишь одним экспертом (особые). Спрашивается, сколько ещё экспертов k следует опросить, чтобы вероятность Рm + k появления содержательно нового предложения стала меньше α= 0,05?