Реферат.Высшая математика.К.А.. Реферат Высшая математика Нахождение производных функций одной переменной, заданных параметрически

• Название: Реферат Высшая математика Нахождение производных функций одной переменной, заданных параметрически
• Дата: 30.04.2023
• Размер: 177.16 Kb.
• Имя файла: Реферат.Высшая математика.К.А..docx
• Тип: Реферат; #1098858
• страница: 5 из 9

ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ, ФУНКЦИИ, ЗАДАННОЙ НЕЯВНО И ПАРАМЕТРИЧЕСКИ

1. 
   Производная сложной функции.
   
2. 
   Производная неявной функции.
   
3. 
   Логарифмическая производная.
   
4. 
   Производная функции, заданной параметрически.
   

Если

1. Производная сложной функции

Теорема

1. 
   y
   

ft

• 
  ^{сложная функция (} t ^{– независимая переменная,  –}
  

промежуточный аргумент);

²⁾ f^x₀  ^и

то

^t₀ ^{, где}

x₀  t₀ ^,

Доказательство

ft^

tt₀

^{ fx}₀ ^{ t}₀ ^.

^{Рассмотрим} t₀  t

 x t₀  t t₀ ^.

^x

y

fx₀  x fx₀ ^.

Рассмотрим

y_ y_ x_.

Пусть

t

t 0 .

x t

Но, так как  lim

x _


x 0 .

t0 _t

При этом
 lim

y _

x0 _x

 lim

y_


lim

^y lim

x_

f^x

 ^t

  ft

^ ,

t0 _t

x0 <sub>x

t0 t</sub> 0 0 0

что и требовалось доказать.

Замечание

В приведенном доказательстве независимая переменная обозначалась ^{символом} t^{, промежуточная переменная – символом} x^{. Чаще встречается}

y fu^{, u x. Тогда}


y^  fx^  f^u u'x.



Пример

y e^{arctg x}, ^y' – ?

Решение

y  e^u, ^{u arctg x}.

y^  e^u u'  e^{arctg x1} .

1  x²

Дифференциалсложнойфункции

y fx^{, u x,}

y^_x

f_u^  u^_x^.

dy

f_u^  u^_xdx

f_u^du^.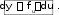

Сравним с формулой
Вывод

dy

f'xdx^.

Дифференциал функции равен произведению производной функции на дифференциал аргумента, при этом не важно, является этот аргумент промежуточным или независимой переменной – инвариантностьформы первого дифференциала.