Реферат.Высшая математика.К.А.. Реферат Высшая математика Нахождение производных функций одной переменной, заданных параметрически
 Скачать 177.16 Kb. Скачать 177.16 Kb.
|
Производные гиперболических функций ex e x sh x , 2 ch x ex e x , 2 th x ex e x ex e x , cth x ex e x ex e x. 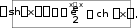 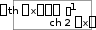 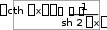 ( x 0 ). ( x 0 ).Пример y sh35x cos2 x. 2 y 3sh 2 5x ch5x 5 cos2 x sh35x 2 cos x sin x 1 2 sh 2 5x cos x15ch 5x cos x sin 2 2 2 x sh 5x . 2 2 2 Производная функции, заданной параметрическиРассмотрим функцию, заданную параметрическим способом x xt , y yt. В этом случае связь аргумента x со значением функции y осуществляется через параметр t. Как вычислить Теорема yx?  Если Если1) xt, yt дифференцируемы ( xt, yt) на интервале ,, и xt строго монотонна на ,; 2) xt 0 то t,, 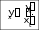 Доказательство Рассмотрим систему равенств y yt, t tx, где t– промежуточный аргумент, y– сложная функция аргумента x. По теореме о производной сложной функции производной обратной функции yx yt tx. По теореме о t t 1 . Таким образом, x x y yt , что и требовалось доказать. t x x Пример x t2 , 3 y t , t ,0. yx– ? Решениеxt 2t , yt 3t2 , y 3 t. x 2 ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВПроизводные высших порядков. Дифференциалы высших порядков. Производные высших порядковОпределение  f x fx f x fxвтораяпроизводная– первая производная от производной первого порядка; fnx fn1x производная n-гопорядка– первая производная от производной n 1-го порядка. Примеры y sin x. y cos x , y sin x , y cos x. y xn. y n xn1 , y nn1xn2 , … yk nn1...n k1xnk ( k n). y ex. yn ex. Вторая производная от неявной функцииПусть неявная функция yаргумента xзадается равенством Fx, y 0. Правило  Для отыскания высшей производной от yпо x , нужно соответствующее число раз дифференцировать заданное равенство, помня, что yи все ее производные являются функциями независимой переменной x. Для отыскания высшей производной от yпо x , нужно соответствующее число раз дифференцировать заданное равенство, помня, что yи все ее производные являются функциями независимой переменной x.Пример y2 x2 1. y – ? 2y y 2x 0 y x, y 2y 2 2y y 2 0 y 1 y2 y x2 y2 . y3 Вторая производная функции, заданной параметрическиРассмотрим функцию y, заданную параметрическим способом x xt , y yt. Выше была получена формула для первой производной этой функции yx yt. xt Новая задача – вычисление второй производной yxx– ? yt y x y x 1 y x y x yxx yx'x t tx t t t t t 2 t t t . 3 xt xt xt xt  Пример x at sin t, y a1 cost, t . yx– ? yxx– ? yx a sin ta1 cost , t ctg 2 xx a1 cos t y . Дифференциалы высших порядковДифференциал независимой переменной, как было показано выше, равен ее приращению dx x, которое независитотx! Дифференциал функции dy fxdx при фиксированном dx– зависит от аргумента x , то есть является функцией. Поэтому можно поставить вопрос о дифференциале этой функции или дифференциале дифференциала. Дифференциал дифференциала функции – второй дифференциал функции или дифференциал второго порядка. Определения и обозначения d2 fx ddfx – дифференциал второго порядка; d2 fx ddfx – дифференциал второго порядка;d3 fx dd2 fx – дифференциал третьего порядка; … dnfx ddn1 fx – дифференциал n-го порядка. Формула для вычисления второго дифференциалаfx ddfx d fxdx dx- константа выносится за d dx dfx dxfxdx f xdx2 f xdx2 *. Здесь x– независимая переменная. Замечание  Форма второго дифференциала не инвариантна. Форма второго дифференциала не инвариантна.Аналогично d3 fx fxdx3. Пусть fx x, тогда fx 0 d2x 0 . fx 0 d3x 0 и так далее. Вывод  Дифференциалы высших порядков от независимой переменной равны нулю. Дифференциалы высших порядков от независимой переменной равны нулю.ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯТеорема Ролля. Теорема Лагранжа. Теорема Коши.  Если ЕслиТеорема РолляТеоремаРолля(онулепроизводной) fx – непрерывна на a,b; 2) fx на a,b; 3) fa fb,  то a,b:  * Подчеркнем, что dx2 dx2 . Доказательство Так как fx непрерывна на a,b, она достигает на a,b наибольшего Mи наименьшего mзначений. Возможны два случая. M m. Тогда fx M m f x – const. fx 0 . M m. Тогда хотя бы одно из этих значений достигается внутри a,b, то есть в точке Пусть a,b,так как f M, где fa fb. a, b. Так как – внутренняя точка, то f. Докажем, что f 0. f lim x0 fxf. x f f x x. lim x00 fxf x fправ 0 , (*) lim x00 fxf x fлев 0. (**) Но из существования f следует, что f fправ fлев f 0 с учетом (*) и (**), что и требовалось доказать. Аналогично выполняется доказательство для f m. Теорема доказана. Геометрическая интерпретацияЕсли функция удовлетворяет условиям теоремы Ролля на отрезке a, b, то в некоторой точке отрезка ее касательная параллельна оси OX. 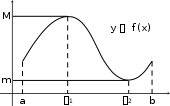 Теорема Ролля позволяет узнать об обращении производной в нуль без ее вычисления. Пример fx xx1x 2x 3. Доказать, что все корни уравнения 3,0. Доказательство f x 0 принадлежат интервалу f0 f1 f 2 f 3 0 . Для каждого из отрезков 3,2, 2,1, 1,0 выполняются условия теоремы Ролля, следовательно, есть три точки, по одной на каждом из соответствующих интервалов, в которых производная обращается в нуль. Замечание  Все условия теоремы Ролля необходимы для справедливости ее утверждения. Все условия теоремы Ролля необходимы для справедливости ее утверждения.Непрерывностьна a,b. 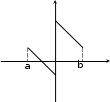 Дифференцируемостьна a, b. 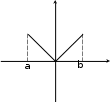 Равенствоfa fb. 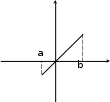  Если ЕслиТеорема ЛагранжаТеоремаЛагранжа fx – непрерывна на a,b; 2) fx – на a,b, то 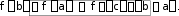 ca,b: Доказательство Введем обозначение fbfa Q. b a Рассмотрим вспомогательную функцию Fx fx fa Qx a. Функция 1) 2) 3) Fx удовлетворяет всем условиям теоремы Ролля: Fx непрерывна на a, b; Fx на a, b; Fa Fb 0 . Следовательно, c: ca,b, Fc 0 . Далее Fx fx Q, Fc fc Q 0, fc Q, fbfa b a fc, что и требовалось доказать. Геометрический смысл теоремы Лагранжа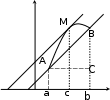 CBfbfa угловой коэффициент секущей AB. x c. AC fc b a угловой коэффициент касательной к кривой y fx в точке На дуге ABнайдется, по крайней мере, одна точка M , в которой касательная параллельна хорде AB теорема Ролля является частным случаем теоремы Лагранжа.  Доказанная формула называется формулой Лагранжа или формулой конечныхприращений. Доказанная формула называется формулой Лагранжа или формулой конечныхприращений.Так как a c b, то c a b a. c a b a, где 0 1 c a b a. 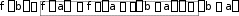 – другая редакция формулы Лагранжа. – другая редакция формулы Лагранжа.Замечание3  Точек cможет быть несколько. Точек cможет быть несколько.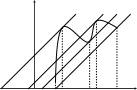 ac1 c2 c3 b Замечание4  Если Еслиfa fb, то fc 0 – утверждение теоремы Ролля. Замечание5  Теорему Лагранжа можно использовать для приближенных вычислений. Теорему Лагранжа можно использовать для приближенных вычислений.fb fa fa b ab a, 0 1. Положим 1 , тогда 2 fb fa f abb a. 2 Погрешность тем меньше, чем ближе bк a. Пример b 1,1, a 1,0 , arctg1,1 – ? |
