Теория экономического анализа. Руководство по изучению дисциплины цели и задачи дисциплины
 Скачать 1.86 Mb. Скачать 1.86 Mb.
|
Пример 2:Составить кратную модель и определить степень влияния каждого фактора на величину результативного показателя одним из возможных приемов детерминированного факторного анализа для данного типа факторной модели. На основании расчетов сделать соответствующие выводы.Исходные данные для факторного анализа безубыточного объема выпуска и продажи продукции
Х – безубыточный объем продажи продукции С – условно-постоянные издержки МД – маржинальный доход с единицы продукции Факторная модель: Применение способа цепной подстановки: 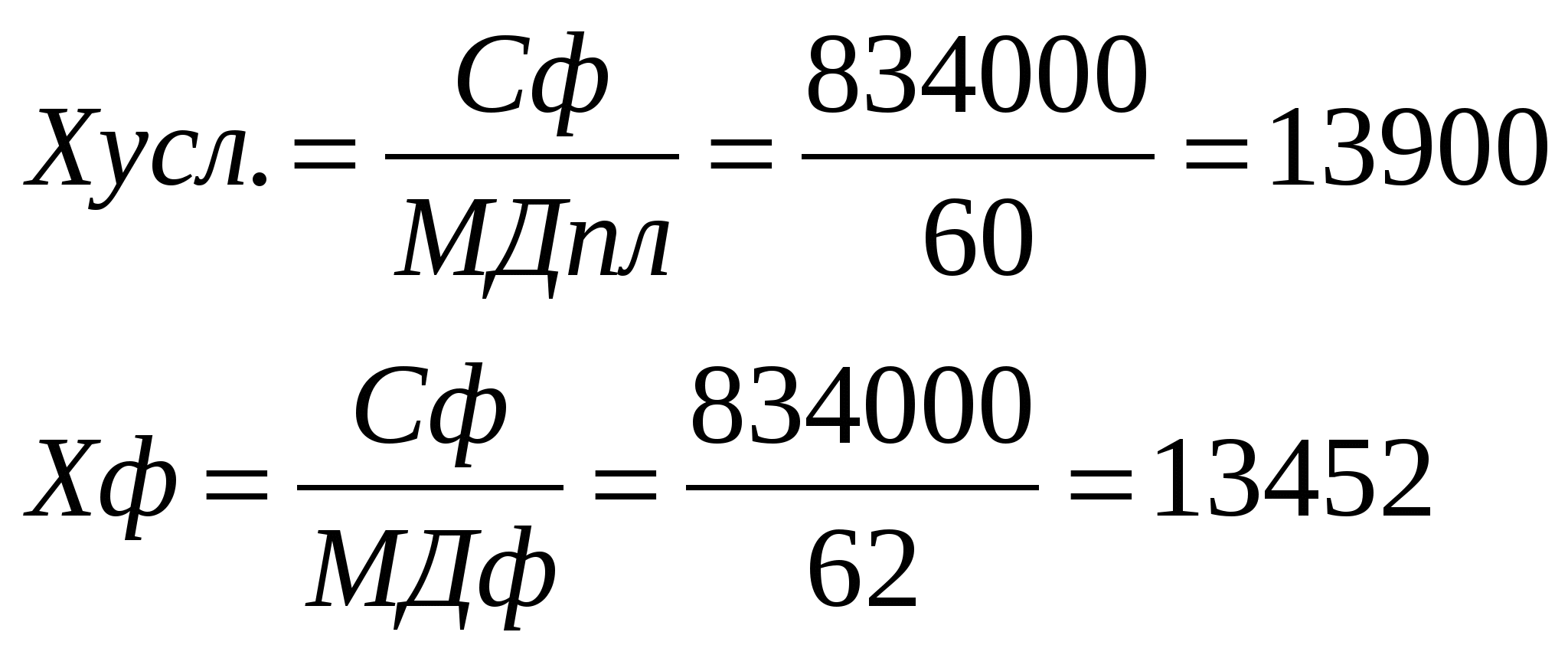 Применение интегрального способа: Вывод: Безубыточный объем продаж – это количество единиц продукции, которую необходимо продать, чтобы покрыть затраты, после чего каждая дополнительная единица проданной продукции будет приносить предприятию прибыль. На анализируемом предприятии безубыточный объем продаж удалось снизить по сравнению с планом на 965 единиц. За счет сокращения суммы условно-постоянных издержек на 31 тыс. руб. безубыточный объем продаж уменьшился на 517 ед. За счет увеличения маржинального дохода с единицы продукции на 2 руб. безубыточный объем продаж уменьшился на 448 ед. Сокращение безубыточного объема продажи продукции позволит укрепить финансовое состояние предприятия. Пример 3:Составить смешанную модель и определить степень влияния каждого фактора на величину результативного показателя методом цепных подстановок Исходные данные для факторного анализа безубыточного объема продажи продукции
Х – безубыточный объем продажи продукции С – условно-постоянные издержки Ц – цена единицы продукции П – переменные издержки на единицу продукции Факторная модель: Применение способа цепной подстановки: Вывод: Общее сокращение безубыточного объема продаж на анализируемом предприятии составило 69 единиц продукции. Увеличение цены реализации с 76 руб. до 78 руб. позволило снизить безубыточный объем продаж на 477 единиц. Рост постоянных издержек на 6 тыс. руб. увеличил безубыточный объем продаж на 176 единиц продукции, а рост переменных издержек на единицу продукции на 1 руб. увеличил безубыточный объем продаж на 232 единицы продукции. Таким образом, резервом сокращения безубыточного объема продаж и увеличения суммы прибыли на анализируемом предприятии является снижение уровня постоянных и переменных издержек ТЕМА 7. СПОСОБЫ СТОХАСТИЧЕСКОГО ФАКТОРНОГО АНАЛИЗА 7.1. Сущность и этапы стохастического анализа Статистические методы изучения связей, называемые иначе стохастическим моделированием, используются в анализе хозяйственной деятельности, когда необходимо: -оценить влияние факторов, по которым нельзя построить жестко детерминированную модель; -изучить и сравнить влияние факторов, которые невозможно включить в одну и туже детерминированную модель; -выделить и оценить влияние сложных факторов, которые не могут быть выражены одним определенным количественным показателем. При построении стохастической модели должны выполняться некоторые условия: -если жестко детерминированную модель можно анализировать и строить по одному объекту, то для стохастической модели необходима совокупность; -необходим достаточный объем наблюдений, в теории статистики считается, что количество наблюдений должно в 6-8 раз превышать количество факторов; -случайность наблюдений; -наличие однородности совокупности (показателем количественной однородности совокупности данных является показатель вариации); -наличие специального математического аппарата (например, инструменты анализа автокорреляций для анализа рядов динамики). Стохастическое моделирование предназначено для решения трех основных задач: -установление самого факта наличия (или отсутствия) статистически значимой связи между изучаемыми признаками; -прогнозирование неизвестных значений результативных показателей по заданным значениям факторных признаков (задачи экстраполяции и интерполяции); -выявление причинных связей между изучаемыми показателями, измерение их тесноты и сравнительный анализ степени влияния. Проведение стохастического моделирования включает в себя следующие этапы: Этап 1. – качественный анализ, в него входят: -постановка цели анализа; -определение совокупности включаемых в анализ данных; -определение результативных признаков; -определение факторных признаков; -выбор периода анализа; -выбор метода анализа. Этап 2. – предварительный анализ моделируемой совокупности, что подразумевает: -проверку однородности совокупности; -исключение аномальных наблюдений; -уточнение необходимого объема выборки; -установление законов распределения изучаемых переменных. Этап 3. – построение регрессионной модели экономического объекта, который включает: -перебор конкурирующих вариантов моделей; -уточнение перечня факторов, включаемых в модель; -расчет оценок параметров уравнений регрессии. Этап 4. – оценка адекватности модели, которая заключается в следующем: -проверка статистической значимости уравнения в целом и его отдельных параметров; -проверка соответствия формальных свойств полученных оценок задачам исследования. Этап 5. – экономическая интерпретация и практическое использование модели. Под этим понимается: -определение пространственно-временной устойчивости зависимостей; -оценка прогностических свойств моделей. Рассмотрим некоторые аспекты осуществления процедур стохастического анализа. Во-первых, для анализа следует брать всю имеющуюся совокупность данных. Если она слишком велика, следует внимательно отнестись к составлению выборки из этой совокупности. Выборка должна быть типичной для данного круга явлений. В противном случае анализ не будет иметь смысла, поскольку его результаты не позволят делать значимые выводы для всей совокупности. Во-вторых, в качестве результативных признаков берут либо показатели эффекта (выручка, товарооборот, объем реализации), либо показатели эффективности (рентабельность, оборачиваемость и т.п.). Следует отметить, что в анализе более предпочтительным является использование относительных показателей. В-третьих, в качестве факторных признаков следует брать показатели, комплексно характеризующие изучаемое явление. При этом также лучше ориентироваться на относительные показатели. В-четвертых, существует два подхода к анализу явлений: статический и динамический. Статический подход встречается чаще, потому что проведение его проще и не требует использования сложных математических методик. Динамический анализ (анализ рядов данных во времени) нередко предполагает рассмотрение автокорреляционных зависимостей, что требует от аналитика владения сложным эконометрическим инструментарием. В-пятых, предварительная обработка рядов данных начинается с установления законов распределения: распределение данных должно быть близко к нормальному. В-шестых, если совокупность неоднородна, следует исключить из нее самые «аномальные» наблюдения, поскольку они, скорее всего, нетипичны для данного исследования. В-седьмых, уточнение перечня факторов может осуществляться, например, путем расчета матрицы парных коэффициентов корреляции. Перебор конкурирующих вариантов моделей, как правило, осуществляется с использованием компьютера. В-восьмых, проверка устойчивости модели осуществляется расчетом ее параметров на усеченной или расширенной совокупности, а также по той же совокупности, но в другом временном интервале. 7.2. Корреляционный анализ Корреляционный анализ – это метод установления связи и измерения ее тесноты между наблюдениями, которые можно считать случайными и выбранными из совокупности, распределенной по многомерному нормальному закону. Корреляционной связью называется такая статистическая связь, при которой различным значениям одной переменной соответствуют разные средние значения другой. Основной особенностью корреляционного анализа является то, что он устанавливает лишь факт наличия связи и степень ее тесноты, не вскрывая ее причин. Степень тесноты связи оценивают коэффициентами, изменяющимися в пределах от -1 до +1. Малое значение коэффициента свидетельствует о слабой связи. Значение, по величине близкое к единице (1,0) характеризует очень сильную связь и часто позволяет предположить наличие функциональной причинно-следственной связи. Значение коэффициента близкое к минус единице (-1) свидетельствует о наличии жестко детерминированной обратно пропорциональной связи между факторами. Если линейной связи между факторами не наблюдается, то значение коэффициента равно нулю (0). Другие значения коэффициента корреляции свидетельствуют о наличии стохастической связи, причем чем ближе его значение по модулю к единице, тем связь теснее. Параметрический корреляционный анализ наиболее распространенный и наиболее точный вид анализа, для которого разработано всестороннее вероятностное обоснование. Условием обоснованного применения параметрических методов анализа, как правило, является нормальный закон распределения данных, используемых для обработки. Оценку наличия линейной связи между переменными проводят с помощью коэффициента корреляции Пирсона. Непараметрические методы статистики, в отличие от параметрических, не базируются на каких-либо предположениях о законах распределения данных. В качестве непараметрических критериев связи переменных часто используют коэффициент ранговой корреляции Спирмена и коэффициент ранговой корреляции Кендалла. 7.3. Регрессионный анализ Регрессионный анализ - это метод установления аналитического выражения стохастической зависимости между исследуемыми признаками. Уравнение регрессии показывает, как в среднем изменяется «у» при изменении любого из хi, и имеет вид: у=f(х1, х2, …хn), где «у» – независимая переменная (она всегда одна); хi – независимые переменные (факторы), их может быть несколько. Если независимая переменная одна – это простой регрессионный анализ, если же их несколько, то такой анализ называется многофакторным. Регрессионный анализ позволяет производить расчет регрессионных моделей путем определения значений параметров – постоянных коэффициентов при независимых переменных (факторах); проверять гипотезу об адекватности модели имеющимся наблюдениям; использовать модель для определения значений зависимой переменной при новых или ненаблюдаемых значениях независимых переменных. Построение уравнения регрессии осуществляется методом наименьших квадратов, суть которого состоит в минимизации суммы квадратов отклонений фактических значений результативного признака от его расчетных значений. Необходимо отметить, что в экономических исследованиях корреляционный и регрессионный анализы нередко объединяются в один – корреляционно-регрессионный анализ. Подразумевается, что в результате такого анализа будет построена регрессионная зависимость (т.е. проведен регрессионный анализ) и рассчитаны коэффициенты ее тесноты и значимости (т.е. проведен корреляционный анализ). 7.4. Кластерный анализ Кластерный анализ – один из методов многомерного анализа, предназначенный для группировки (кластеризации) совокупности, элементы которой характеризуются многими признаками. Значения каждого из признаков служат координатами каждой единицы изучаемой совокупности в многомерном пространстве признаков. Каждое наблюдение, характеризующееся значениями нескольких показателей, можно представить как точку в пространстве этих показателей, значения которых рассматриваются как координаты в многомерном пространстве. Расстояние между точками p и q с kкоординатами определяется как: Основным критерием кластеризации является то, что различия между кластерами должны быть более существенны, чем между наблюдениями, отнесенными к одному кластеру, т.е. в многомерном пространстве должно соблюдаться неравенство: rp.q где r1.2 – расстояние между кластерами 1 и 2. Процедура класстеризации достаточно трудоемка, ее целесообразно выполнять на компьютере. 7.5. Дисперсионный анализ Дисперсионный анализ – это статистический метод, позволяющий подтвердить или опровергнуть гипотезу о том, что две выборки данных относятся к одной генеральной совокупности. Применительно к анализу деятельности предприятия можно сказать, что дисперсионный анализ позволяет определить, к одной и той же совокупности данных или нет относятся группы разных наблюдений. Дисперсионный анализ часто используется совместно с методами группировки. Задача его проведения в этих случаях состоит в оценке существенности различий между группами. Для этого определяют групповые дисперсии ТЕМА 8 ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ АНАЛИЗА ХОЗЯЙСТВЕННОЙ ДЕЯТЕЛЬНОСТИ И ИХ ПРИМЕНЕНИЕ В РЕШЕНИИ ТИПОВЫХ АНАЛИТИЧЕСКИХ ЗАДАЧ 8.1. Экономико-математическое моделирование как способ изучения и анализа экономических процессов Математическое моделирование экономических явлений и процессов является важным инструментом экономического анализа. Оно дает возможность получить четкое представление об исследуемом объекте, охарактеризовать и количественно описать его внутреннюю структуру, внешние и внутренние связи. Цель данного исследования – количественное обоснование принимаемых решений. При решении конкретной задачи управления применение экономико-математических методов предполагает: -построение экономических и математических моделей для задач принятия решения в сложных ситуациях или в условиях неопределенности; -изучение взаимосвязей, определяющих впоследствии принятие решений, и установление критериев эффективности, позволяющих оценивать преимущество того или иного варианта действия. Под экономико-математической моделью в экономической науке понимается аналог, макет какого-либо экономического процесса или явления. В экономической науке используются главным образом математические модели, описывающие изучаемые явления с помощью математических выражений: неравенств, различных производственных функций, дифференциальных и интегральных уравнений и других математических средств. Составление модели требует понимания сущности описываемого явления и знания математического аппарата. Различают: -математические модели с количественными характеристиками, записанными в виде формул; -числовые модели с конкретными числовыми характеристиками; -логические модели, записанные с помощью логических выражений; -графические модели, выраженные в графических образах. Экономико-математическая модель должна отражать существенные стороны и связи изучаемого объекта, т.е. должна быть адекватна действительности. Процесс моделирования можно условно разделить на три этапа: 1-й этап. Построение модели (лучшей моделью является не самая сложная, а та, которая позволяет получить самое рациональное решение и наиболее точные экономические оценки). При экономико-математическом моделировании часто возникает ситуация, когда изучаемая экономическая система имеет слишком сложную структуру. Такой экономической системой, например, является экономика предприятия в целом, в ее динамике, развитии. Возникает необходимость упрощения изучаемого объекта, исключения и анализа его второстепенных особенностей с тем, чтобы подвести эту упрощенную систему под класс уже известных структур, поддающихся математическому описанию и анализу. При этом степень упрощения должна быть такой, чтобы все существенные для данного экономического объекта черты в соответствии с целью исследования были включены в модель. На первом этапе моделирования осуществляется формулировка конечной цели построения модели, а также определение критерия, по которому будут сравниваться различные варианты решения. В экономическом анализе такими критериями могут выступать: максимум прибыли, минимум издержек производства, максимальная загрузка оборудования, максимальная производительность труда и т.д. Например, в задаче об использовании ресурсов критерий эффективности – прибыль от реализации произведенной продукции, которую нужно максимизировать, в транспортной задаче – суммарные затраты на перевозку грузов от поставщиков к потребителям, которые нужно минимизировать. Выбор критерия эффективности определяет практическую ценность исследования; 2-й этап. Определение и разработка методов, с помощью которых можно решить смоделированную задачу; 3-й этап. Анализ полученных результатов, т.е. экономическая интерпретация решения, полученного при изучении экономического явления или процесса. Окончательным критерием достоверности и качества модели являются: практика, соответствие полученных результатов и выводов реальным условиям производства, экономическая содержательность полученных оценок. Если полученные результаты не соответствуют реальным производственным условиям, то необходим экономический анализ причин несоответствия. Такими причинами могут быть недостаточная достоверность информации, а также несоответствие используемых математических средств и схем особенностям и сущности изучаемого экономического объекта. После того как причина определена, в модель должны быть внесены соответствующие коррективы, и решение задачи осуществляется заново. 8.2. Классы задач экономических исследований По своей содержательной постановке множество задач исследования может быть разбито на ряд классов: -задачи сетевого планирования и управления рассматривают соотношения между сроками окончания крупного комплекса операций или работ и моментами начала всех операций комплекса. Эти задачи состоят в нахождении минимальных продолжительностей комплекса операций, оптимального соотношения величин стоимости и сроков их выполнения; -задачи массового обслуживания посвящены изучению и анализу систем обслуживания с очередями заявок или требований и состоят в определении показателей эффективности работы систем, их оптимальных характеристик, например, в определении числа каналов обслуживания, времени обслуживания и т.д.; -задачи управления запасами состоят в отыскании оптимальных значений уровня запасов и размера заказа. Особенность таких задач заключается в том, что с увеличением уровня запасов, с одной стороны, увеличиваются затраты на их хранение, но с другой стороны, уменьшаются потери вследствие возможного дефицита запасаемого продукта; -задачи распределения ресурсов возникают при определенном наборе операций или работ, которые необходимо выполнять при ограниченных наличных ресурсах, и требуется найти оптимальные распределения ресурсов между операциями или состав операций; -задачи ремонта и замены оборудования актуальны в связи с износом и старением оборудования и необходимостью его замены с течением времени. Задачи сводятся к определению оптимальных сроков, числа профилактических ремонтов и проверок, а также моментов замены оборудования модернизированным; -задачи составления расписания (календарного планирования) состоят в определении оптимальной очередности выполнения операций на различных видах оборудования; -задачи планировки и размещения состоят в определении оптимального числа и места размещения новых объектов с учетом их взаимодействия с существующими объектами и между собой; -задачи выбора маршрута или сетевые задачи, чаще всего встречаются при исследовании разнообразных задач на транспорте и в системе связи и состоят в определении наиболее экономичных маршрутов; -задачи принятия оптимальных решений в конфликтных ситуациях, изучаемые теорией игр. 8.3. Линейное программирование Линейное программирование относится к методам оптимизации. Оптимизация – это процесс выбора наилучшего плана из множества решений по выбранному критерию оптимальности. Оптимальный план – это решение, полученное в результате процесса оптимизации. Оптимальный план при статической информации не всегда бывает долговечен в связи с постоянно меняющейся информацией, которая используется при решении задачи. Очень часто оптимальные планы становятся рациональными, т.е. близкими к оптимальному плану. Использование математических методов в анализе и в планировании деятельности экономической системы позволяет автоматизировать процесс поиска рациональных решений, сократить время вычислительной работы для поиска решения и найти наилучший вариант. Наиболее простым из универсальных методов линейного программирования, широко применяемым на практике в анализе и планировании деятельности любой экономической системы, является симплексный метод и его модификация. Применение симплекс-метода осуществляется в два этапа: -нахождение исходного допустимого базового решения; -последовательное улучшение полученного на первом этапе решения до достижения оптимального решения. Метод линейного программирования наиболее распространенный в прикладных экономических исследованиях. Суть метода линейного программирования заключается в поиске максимума или минимума выбранной в соответствии с интересами аналитика целевой функции при имеющихся ограничениях. Пример: Фабрика по производству чая выпускает две марки этого продукта (А и В). Отпускная цена чая марки «А» – 60 руб. за килограмм, марки «В» – 50 руб. за килограмм. Каковы должны быть оптимальные годовые объемы производства чая обеих марок, чтобы выручка фабрики от их реализации была максимальной. Пусть оптимальный объем производства чая марки «А» составит х тонн в год, а марки «В» – у тонн в год. Суммарная выручка от их реализации составит (60х+50у) тыс. руб. Решение задачи подразумевает поиск такой комбинации (х, у), которая позволила бы обеспечить максимум этой функции, т.е. поиск 60х+50у Понятно, что чем больше будет выпуск и той, и другой марки, тем больше будет выручка, однако ресурсы фабрики не безграничны. Для изготовления обоих сортов чая используется одно и то же оборудование, общая производительность которого составляет 300 тонн продукции в год. Таким образом, ограничение по мощности оборудования выглядит следующим образом: х + у При изготовлении чайных смесей разных марок используют чайный лист двух сортов: в состав чая марки «А» входит 70% 1-го сорта и 30% 2-го сорта, а в состав марки «В» – 20% 1-го сорта и 80% 2-го сорта. Стоимость сырья 1-го сорта составляет 38 руб. за килограмм, 2-го сорта – 24 руб. за килограмм. Таким образом, себестоимость чайного листа, необходимого для производства одного килограмма чая марки «А», составляет 33,8 руб. (0,7 Фабрика может тратить на закупку сырья не более 9000 тыс. руб. в год. Следовательно, на объем выпуска накладывается еще одно ограничение финансового порядка: 33,8х + 26,8у Понятно, что искомые величины объемов производства разных сортов чая (х и у) должны быть положительны. Таким образом, полная формулировка задачи линейного программирования в данном случае будет следующей: 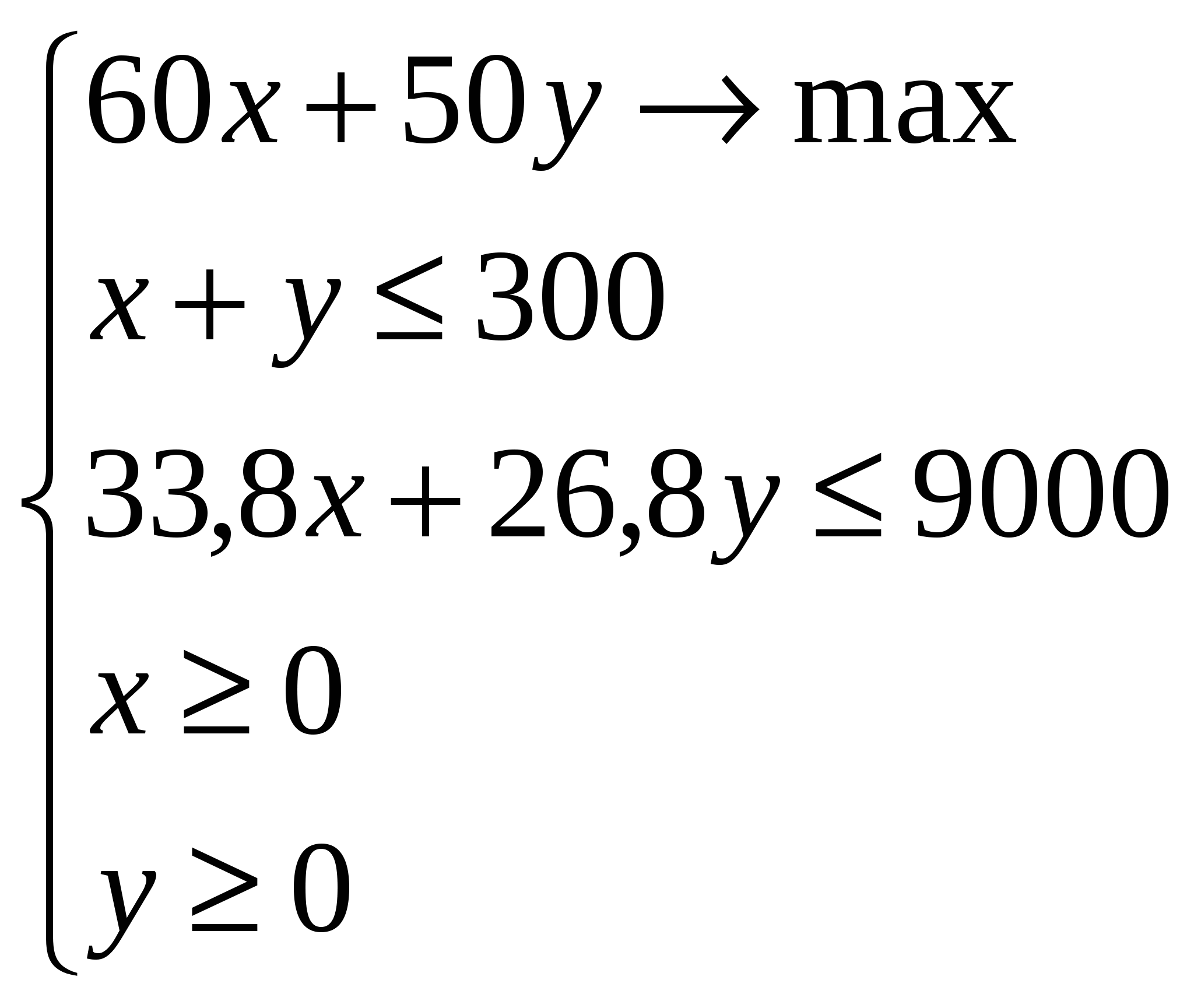 Найденное алгебраическим методом решение этой системы уравнений будет таким: 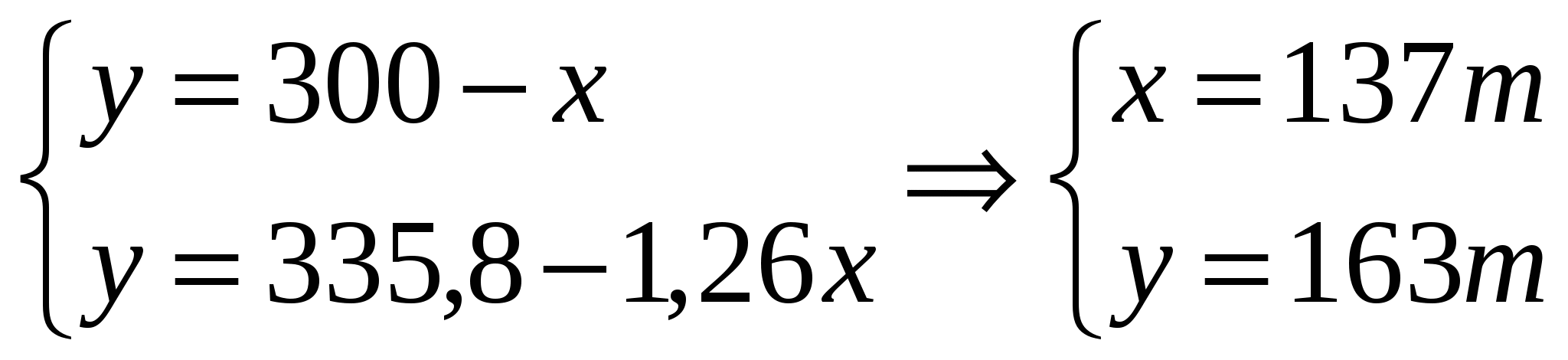 Именно такое соотношение объемов выпуска чая сортов «А» и «В» позволит фабрике при соответствующих технологических и финансовых ограничениях получить максимальный объем выручки. Кроме задач оптимизации выпуска с помощью метода линейного программирования решаются так называемые транспортные задачи и задачи составления расписания 8.4. Динамическое программирование Динамическое программирование относится к вычислительному методу, использующему аппарат рекуррентных соотношений, разработанный американским ученым Р. Беллманом. Термин «динамическое программирование» возник в результате изучения задач математического программирования, в которых ряд условий изменялся во времени. Однако этот метод можно использовать в задачах, где время вообще отсутствует. Динамическое программирование – это метод оптимизации решений, специально приспособленный к так называемым многошаговым или многоэтапным операциям. Любую многошаговую задачу можно решать по разному: либо искать сразу все элементы решения на всех шагах, либо же строить оптимальное управление шаг за шагом, на каждом этапе расчета оптимизируя только один шаг. Оптимизация одного шага, как правило, проще оптимизации всего процесса: лучше много раз решить сравнительно простую задачу, чем один раз сложную. Но управление на отдельном шаге выбирается не так, чтобы выигрыш именно на данном шаге был максимальным, а так, чтобы сумма выигрышей была максимальной на всех оставшихся до конца шагах плюс данный. Если модели линейного программирования можно использовать в экономике для принятия крупномасштабных плановых решений в сложных ситуациях, то модели динамического программирования применяются при решении задач значительно меньшего масштаба, например, при разработке правил управления запасами, устанавливающими момент пополнения запасов и размер пополняющего заказа; при разработке принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию; при распределении дефицитных капитальных вложений между возможными новыми направлениями их использования; при составлении календарных планов текущего и капитального ремонта сложного оборудования и его замены; при разработке долгосрочных правил замены выбывающих из эксплуатации основных фондов и т.п. 8.5. Теория массового обслуживания При исследовании экономических явлений часто приходится сталкиваться с системами, предназначенными для многоразового использования при решении однотипных задач. Возникающие при этом процессы получили название процессов обслуживания, а системы – систем массового обслуживания. Теория массового обслуживания – новое научное направление, возникновение которого было вызвано потребностью практики в анализе процессов и систем, приводящих к очередям в обслуживании. Очереди возникают в различных сферах человеческой деятельности: в промышленном производстве, в торговле, в сфере услуг, в бытовом, медицинском или ином обслуживании. В более широком смысле очереди формируются и в ходе различных процессов, там, где возможно скопление деталей изделий, полуфабрикатов, прежде чем они пройдут через соответствующую производственную операцию. В большинстве случаев очередь принимает вид некоторой последовательности этих проектов, т.е. определенной организации их скопления. Примерами систем массового обслуживания являются телефонные системы, ремонтные мастерские, билетные кассы, магазины, работа экспедиции на предприятиях пищевой, мясной и молочной промышленности и т.д. Системы массового обслуживания характеризуются тремя основными факторами: -входящим потоком требований; -механизмом обслуживания; -дисциплиной обслуживания. Под требованием на обслуживание понимается потребность в обслуживании, исходящая от какого-либо объекта (например, в работе автосервиса под требованием выступает автомашина, ожидающая ремонта или технического обслуживания; в работе экспедиции колбасного завода под требованием выступает автомашина, прибывшая за получением колбасных изделий и других мясопродуктов). Технические средства и производственный персонал, выполняющие функции обслуживания, называются каналами обслуживания. (Например в работе автосервиса каналом обслуживания выступает слесарь, производящий ремонт автомобиля; в работе экспедиции предприятия каналом обслуживания является кладовщик, отпускающий продукцию.). Совокупность, в которой последовательно связаны между собой поток требований на обслуживание, очередь и каналы обслуживания, представляет собой систему массового обслуживания. Очередь образуется в следующих случаях: -пропускная способность канала обслуживания явно не соответствует числу поступающих требований; -требования поступают нерегулярно и носят случайный характер; -время обслуживания носит случайный характер: одно требование занимает больше времени, другое – меньше; -входящий поток требований и время обслуживания носят случайный характер. Цель теории массового обслуживания состоит в анализе процесса образования очередей, в определении взаимосвязей между их основными характеристиками и в конечном счете в нахождении оптимальных путей управления этими процессами. 8.6. Теория игр и область ее применения На практике часто приходится сталкиваться с задачами, в которых необходимо принимать решения в условиях неопределенности, т.е. возникают ситуации, в которых две или более стороны преследуют различные цели, а результаты любого действия каждой из сторон зависят от мероприятий партнера. В экономике конфликтная ситуация порождается различием интересов партнеров и стремлением каждого из них принимать оптимальные решения, которые реализуют поставленные цели в наибольшей степени. При этом каждому приходится считаться не только со своими целями, но и с целями партнера и учитывать неизвестные заранее решения, которые эти партнеры будут принимать. Для грамотного решения задач с конфликтными ситуациями необходимы научно обоснованные методы. Такие методы разработаны математической теорией конфликтных ситуаций, которая называется теорией игр. Предметом теории игр выступают такие ситуации, в которых протекают конфликты и совместные действия игроков. Математическая модель конфликтной ситуации называется игрой, стороны, участвующие в конфликте – игроками, а исход конфликта - выигрышем. В зависимости от числа игроков, участвующих в конфликтном процессе, различают игры с двумя, тремя, и более участниками. По количеству стратегий различают конечные и бесконечные игры. По свойствам функций выигрыша игры классифицируются на две группы: -игры с нулевой суммой или антагонистические, когда выигрыш одного из игроков равен проигрышу другого; -игры с постоянной разностью, в которых игроки и выигрывают и проигрывают одновременно. Для того чтобы найти решение игры, следует для каждого игрока выбрать стратегию, которая удовлетворяет условию оптимальности, т.е. один из игроков должен получать максимальный выигрыш, когда второй придерживается своей стратегии. В тоже время второй игрок должен иметь минимальный проигрыш, если первый придерживается своей стратегии. Оптимальные стратегии должны также удовлетворять условию устойчивости, т.е. любому из игроков должно быть невыгодно отказаться от своей стратегии в этой игре. Деловые игры представляют собой имитацию каких либо экономических процессов с участием игроков, имеющих расписанные для них роли. Конструктивными элементами любой игровой модели являются: -участники игры; -правила игры; -информационный массив, отражающий состояние и движение ресурсов моделируемой хозяйственной системы. Основными направлениями использования деловых игр являются: -обучение персонала; -аттестация кадров и проверка их компетентности; -исследовательские цели, анализ вариантов различных проектов и альтернатив; -принятие решений, касающихся разработки плана. Моделирование деятельности экономических систем заключается в построении имитационной модели. Имитационная модель является математическим обеспечением игры и позволяет повысить оперативность анализа деятельности экономической системы, дает возможность проводить эксперимент с системой, способствует определению оптимального поведения данной системы в заданном интервале времени. С помощью деловой игры возможен всесторонний анализ применения коммерческих принципов на уровне отрасли, объединения, предприятия, проверка самостоятельности и пригодности выдвинутых экономических концепций. Основой математического обеспечения деловой игры является система экономико-математических моделей, описывающая использование финансовых, трудовых, материальных ресурсов и производственных мощностей. 8.7. Имитационное моделирование Одним из путей совершенствования деятельности экономических систем является использование экономико-математического моделирования и современной вычислительной техники. Имитацией принято называть численный метод проведения экспериментов с математическими и логическими моделями, описывающими поведение сложных систем в течение, как определенного момента времени, так и продолжительных периодов времени. При этом базой проведения такого рода экспериментов является использование ЭВМ и современной компьютерной техники. Использование имитационного моделирования в экономических исследованиях дает ряд преимуществ исследователю: -базируясь на использовании современной вычислительной техники, имитация ускоряет процесс проведения эксперимента, облегчая вычисления, и уменьшает вероятность совершения ошибки; -имитация дает возможность проведения косвенных экспериментов, повторных расчетов без реальных экономических последствий; -имитация позволяет анализировать деятельность системы, как в течение определенного момента времени, так и на длительных отрезках времени; -машинная имитация позволяет оперировать моделями, в большей степени адекватными реальной экономической системе; -пользуясь методом имитации, исследователь получает возможность изменить последовательность свершения различных событий; -вводя в компьютерные программы случайные или псевдослучайные переменные, исследователь получает возможность изучать случайные или стохастические процессы; -использование машинной имитации дает возможность проведения эксперимента с моделью реальной экономической системы, а не с самой системой. Это дает существенный экономический выигрыш и позволяет избежать отрицательных последствий в случае проведения эксперимента с реальной экономической системой. Процесс построения имитационной модели состоит из четырех этапов: 1. Изучение системы. Исследователь собирает достоверную информацию о ее деятельности. На данном этапе выявляются количественные и качественные связи и взаимоотношения элементов системы. Кроме того, прежде чем начать сбор информации, исследователь обязан четко сформулировать цель исследования, которая выступает общим критерием оптимальности имитационной модели. 2. Формулирование и построение комплекса экономико-математических моделей, являющегося основой построения имитационной модели. Совокупность построенных экономико-математических моделей должна быть адекватна реальным процессам, имеющим место в действительности. Иначе полученный результат будет в значительной степени заведомо искажен. Имитационные модели лучше строить в блочной структуре, показывая взаимосвязи отдельных задач. В каждом блоке обязательно должен быть хотя бы один вход и выход. В отдельный блок допускается несколько входов и выходов. При построении блочной структуры имитационной модели не должно быть замкнутых контуров. 3. Проведение расчетов по моделям с помощью компьютера. Этот этап охватывает общую методологию статистического эксперимента на вычислительной машине. 4. Осуществление экономической интерпретации полученного решения. |
