Проектирование и расчет металлических конструкций I. МК Сатылганов Аслан. Сатылганов Аслан рпзс 196
 Скачать 4.52 Mb. Скачать 4.52 Mb.
|
Эпюра моментов (М1Δ+ МР) от ветровой нагрузки:на левой стойке на правой стойке 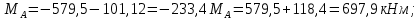 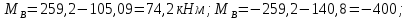 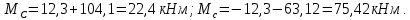 Эпюра Q на левой стойке: 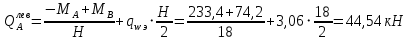 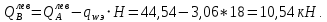 Эпюра Q на правой стойке: 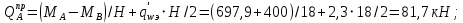 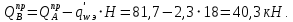 При правильном решение сумма поперечных внизу должна быть равна сумме всех горизонтальных нагрузок. 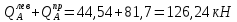 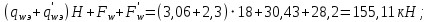 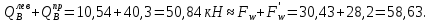  Рисунок 9. Эпюры усилий от ветровой нагрузки а – грузовая эпюра; б – эпюры моментов; в – эпюры поперечных сил. Определение расчетных усилий в сечениях рамыНа основании расчета рамы на отдельные нагрузки необходимо установить неблагоприятные комбинации внутренних усилий в сечениях рамы от совместного действия нагрузок. Для этого составляются возможные комбинации следующих типов: ±Мmax; Nсоот. ±Nmax; Mсоот. ±Nmin; Mсоот. В комбинациях усилий набор нагрузок производится по следующим правилам: постоянная нагрузка учитывается обязательно; горизонтальные крановые усилия могут учитываться только совместно с вертикальными усилиями от кранов (в табл. 2.3 нагрузка 4 с нагрузкой 3 или 4* с 3*). нагрузки 3,4,5 и соответствующие им обратно симметричные 3*,4*,5* являются несовместимыми. Значения усилий в комбинациях устанавливаются с учетом двух видов основных сочетаний нагрузок: постоянная и одна временная нагрузки, здесь коэффициент сочетания ψ=1; постоянная и не менее двух временных нагрузок, где длительная нагрузка умножается на коэффициент сочетания ψ1=0,95, а кратковременная на ψ2=0,9. За одну кратковременную нагрузку принимается: снеговая нагрузка; крановая нагрузка (вертикальная вместе с горизонтальной); ветровая нагрузка. По результатам расчета составлена табл. 2.3 для четырех основных сечений левой колонны рамы. Из возможных комбинаций выбраны (подчеркнутые в таблице 2.3) наиболее неблагоприятные для определения усилий в стержнях стропильной фермы, подбора и проверки сечений колонн, расчета узлов рамы и анкерных болтов. Номера нагрузок для различных комбинаций и сечений отвечают конкретным условиям примера, для других примеров они могут быть иными. Если в комбинации Nmin; Mсоот, при расчете на растяжение анкерных болтов с внутренней стороны колонны, постоянная нагрузка разгружает болты (е=M/N<ρ≈h/2), то усилия от постоянной нагрузки принимаются с коэффициентом по нагрузке γfg=0,9. Ранее принят γfg=1,05, то есть необходимо умножить усилия на поправочный коэффициент 0,9/1,05. При е>ρ такой пересчет не требуется. Поперечная сила Qmax необходима для расчета элементов решетки сквозных колонн, а Qсоот для проверки местной устойчивости стенки сплошных колонн и других расчетов. 3. Расчёт подкрановой балки Расчетные усилия (максимальные изгибающие моменты и поперечные силы) в подкрановых балках находят от двух сближенных кранов наибольшей грузоподъёмности. Предельно допустимый прогиб подкрановых балок: 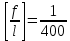 - для кранов групп режимов работы 1К-6К. - для кранов групп режимов работы 1К-6К.Исходные данные. Требуется рассчитать подкрановую балку пролётом 6 м под два крана грузоподъёмностью Qкр= 80/20 т однопролётного производственного здания. Материал балки – сталь С275; Ry =270 МПа (при t ≤ 20 мм); Rs= 0,58⋅ 270 = 157 МПа. Нагрузки на подкрановую балку. По приложению 1 для крана Qкр= 80/20 т режима работы 6К наибольшее вертикальное усилие на колесе 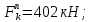 вес тележки Gт= 323 кН. вес тележки Gт= 323 кН.Для кранов режима работы 6К с гибким подвесом груза нормативное вертикальное усилие на колесе 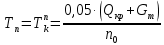 = = 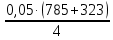 =6.8 кН, =6.8 кН,где Qкр - номинальная грузоподъёмность крана; Gт – масса тележки, n0- число колёс с одной стороны крана. Определение расчётных усилий. Определение расчётного изгибающего момента 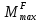 от воздействия вертикальной крановой нагрузки. Допуская, что сечение с максимальным изгибающим моментом расположено в середине пролёта балки и, пользуясь линией влияния момента в этом сечении, устанавливаем краны не выгоднейшим образом от воздействия вертикальной крановой нагрузки. Допуская, что сечение с максимальным изгибающим моментом расположено в середине пролёта балки и, пользуясь линией влияния момента в этом сечении, устанавливаем краны не выгоднейшим образом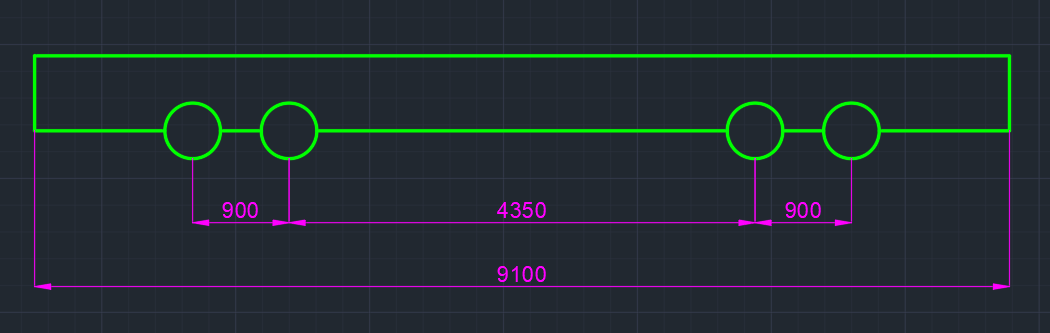 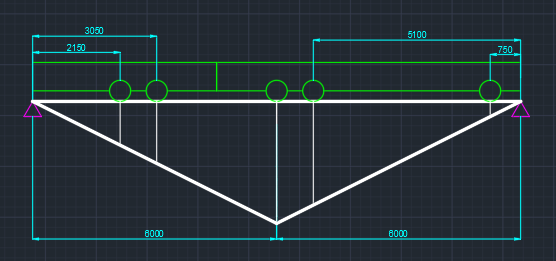 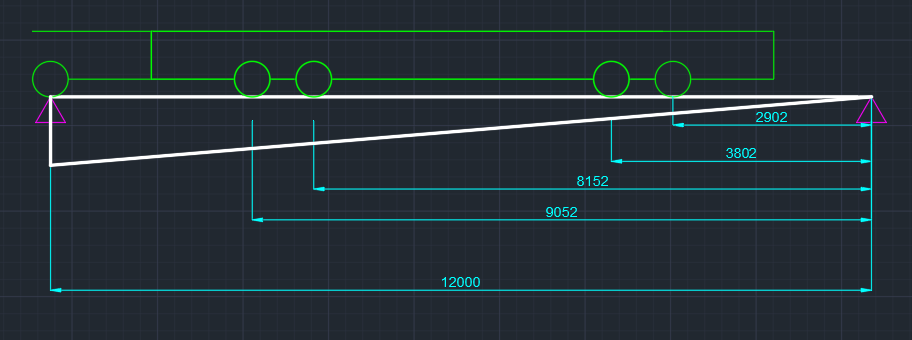 y1 = 12/4=3 y2=0.54 y3=0.76 y4=0.18 y5=1.3 y1 = 1 y2=0.75 y3=0.68 y4=0,32 y5=0,24 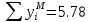 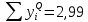 Рисунок 10. Расчётные схемы подкрановой балки а – схема крановой нагрузки; б – к определению Mmax; в – к определению Qmax Расчетный момент от вертикальной нагрузки: 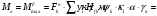 =402*5,78*1,1*0,85*1,1*1,03*0,95=2 338,4 где уi – ординаты линий влияния; γfk= 1,1 – коэффициент надёжности по крановой нагрузке; к =0,85 – коэффициент сочетания крановых нагрузок; к1=1,1 – коэффициент динамичности к вертикальным нагрузкам для подкрановых балок (по таблице 5); α= 1,03 – учитывает влияние собственного веса подкрановых конструкций и временной нагрузки на тормозной площадке (для балок пролётом 12 м α= 1,05 и для полёта 6 м α= 1,03); γn=0,95 – коэффициент надёжности по ответственности. Расчётный момент от горизонтальной крановой нагрузки: 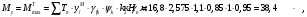 =6,8*5,78*1,1*0,85*1*0,95=34,9 динамичности к горизонтальным нагрузкам (по таблице 5) Для определения максимальной поперечной силы загружаем линию влияния поперечной силы на опоре (рисунок 10,в). Расчётные значения поперечных сил на опоре балки от вертикальной и горизонтальной нагрузок: 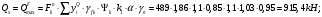 =402*2,99*1,1*0,85*1,1*1,03*0,95=1 209,6 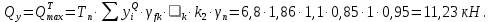 Таблица 5. Значения коэффициентов динамичностей 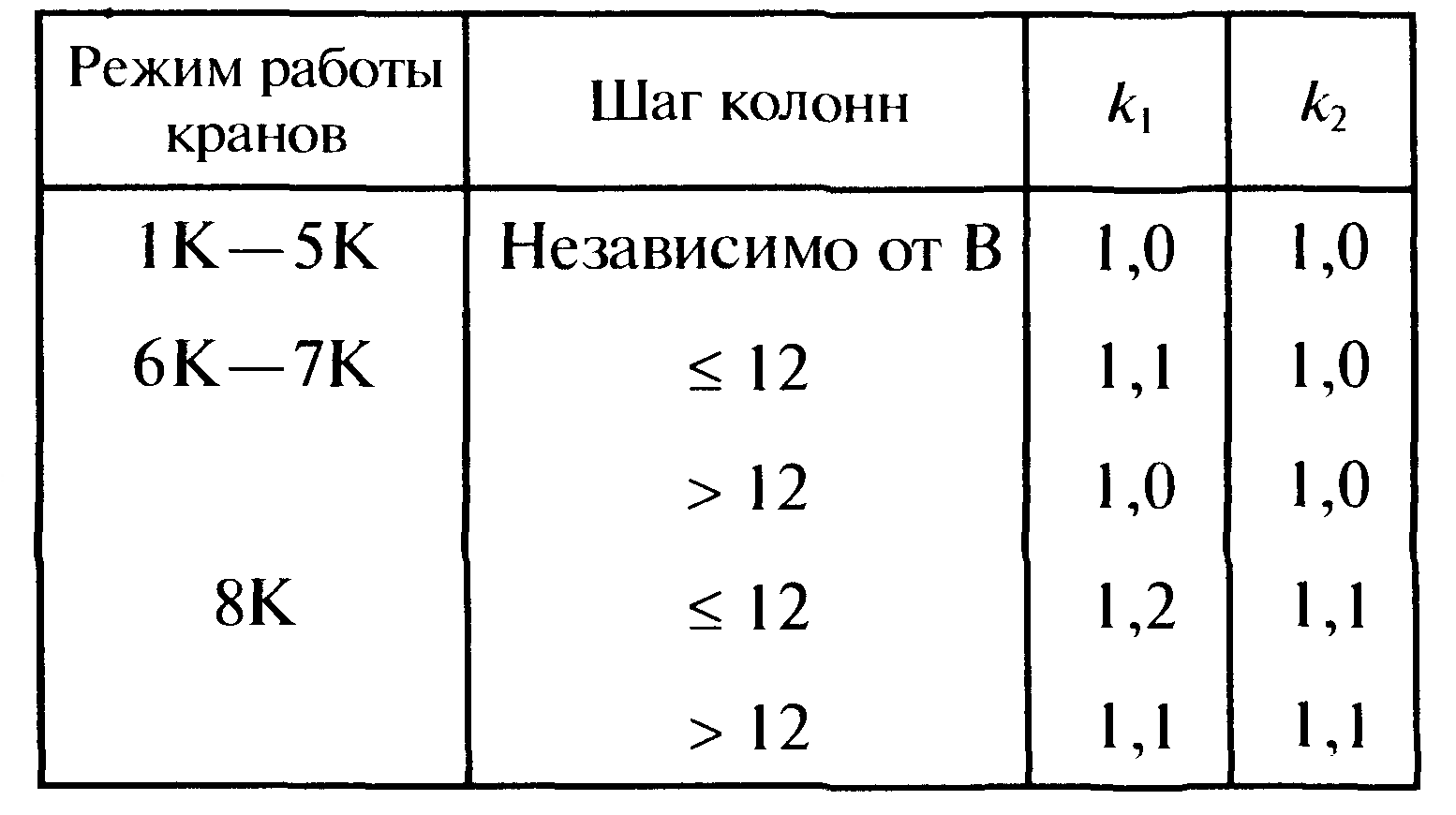 Подбор сечения подкрановой балки Подкрановую балку принимаем симметричного сечения с тормозной конструкцией из рифленой стали толщиной t=6 мм и швеллера №16( при наличие промежуточной стойки фахверка, а также при шаге рам 6 м можно принимать швеллер №16 – 18, а при шаге 12 м – швеллер № 36). Условие прочности в наиболее напряжённой точке «А» сечения 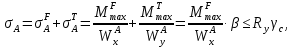 где - коэффициент, учитывающий влияние горизонтальных поперечных нагрузок на напряжение в верхнем поясе подкрановой балки 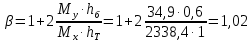 где 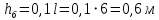 - высота балки, её можно принимать в пределах (1/6…1/10)ℓб; hт= hн=1,0 м - ширина сечения тормозной конструкции. - высота балки, её можно принимать в пределах (1/6…1/10)ℓб; hт= hн=1,0 м - ширина сечения тормозной конструкции.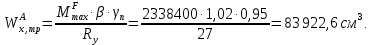 Минимальная высота балки: 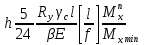 где 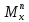 - момент от загружения балки одним краном при - момент от загружения балки одним краном при 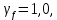 определяемый по линии влияния (рисунок 10,б). определяемый по линии влияния (рисунок 10,б).Сумма ординат линии влияния при нагрузке от одного крана 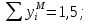 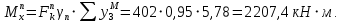 Для кранов группы режима работы 6К 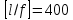 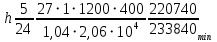 =118,96 =118,96По таблице 6 задаемся гибкостью стенки балки 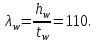 Оптимальная высота по расходу стали : 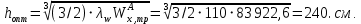 Принимаем hб=240 см (кратной 10 см). Таблица 6 Рекомендуемые соотношения высоты балки и толщины стенки  Задаемся толщиной полок балки tf =2 см, тогда 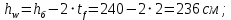 h0 = hб – tf = 240 – 2 = 238 см.  Толщина стенки из условия сопротивления срезу силой Толщина стенки из условия сопротивления срезу силой 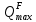 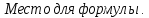 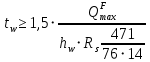 =1,5*1 209,6/236*15,7=0,49 =1,5*1 209,6/236*15,7=0,49Принимаем tст=14 мм, при этом 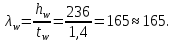 Размеры поясных листов: 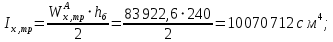 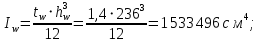 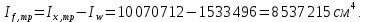 Требуемая площадь поясов: 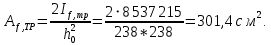 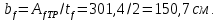 По конструктивным требованиям bf min = 180 мм, поэтому принимаем пояс из стального листа сечением tf x bf = 20 x 180 мм; Af = 36 см2 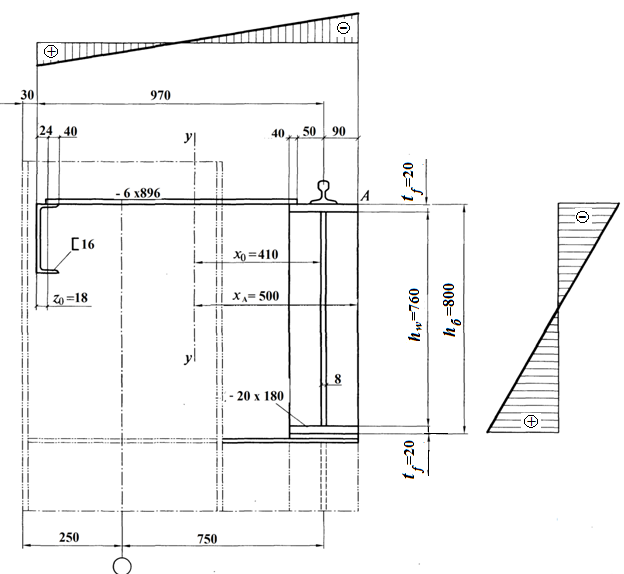      Рисунок 11. Сечение балки Устойчивость сжатого пояса обеспечена так как 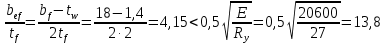 Отношение 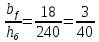 находится в рекомендуемых пределах находится в рекомендуемых пределах 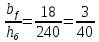 По полученным данным компонуем сечение балки (рисунок 11). Проверка прочности сечения Геометрические характеристики сечения подкрановой балки относительно оси x-x: 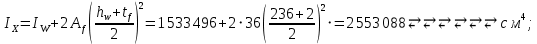 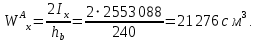 Геометрические характеристики подкрановой балки относительно оси у – у (в состав тормозной балки входят верхний пояс подкрановой балки, тормозной лист и швеллер; площадь поперечного сечения швеллера № 36 А=53,4 см2; ширина тормозного листа 870-70-50=750 мм).(110-40=70) Расстояние от оси подкрановой балки до центра тяжести сечения: 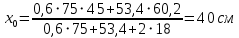 ; ;Расстояние от центра тяжести сечения до наиболее напряженной точки “A” верхнего пояса подкрановой балки: 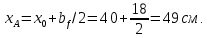 . .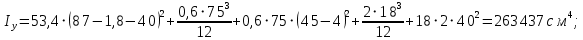 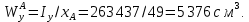 Проверка нормальных напряжений в верхнем поясе (в точке А) подкрановой балки: 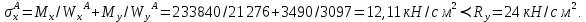 Большой запас прочности получен в связи с увеличением сечения по конструктивным требованиям по сравнению с расчётным. Проверка прогиба подкрановой балки и прочности стенки на действие касательных напряжений на опоре не нужны, так как высота балки hб больше минимального значения hmin , а принятая толщина стенки больше толщины определённой из условия среза. Расчет и конструирование колонны Верхняя часть ступенчатой колонны обычно проектируется сплошной, двутаврового сечения, нижняя часть принимается сплошной при ширине до 1 м, а при большей ширине ее экономичнее делать сквозного сечения. В раме ригель имеет жесткое крепление, поэтому для подбора симметричного сечения верхней части колонны расчетная комбинация усилий М, N устанавливается по сечению 1-1. Для подбора несимметричного сечения сплошной или сквозной нижней части следует рассмотреть несколько возможных комбинаций усилий: расчетные комбинации с + М в нижнем сечении колонны, при котором изгибающий момент догружает наружную ветвь и с -М в сечении под уступом, здесь изгибающий момент догружает подкрановую ветвь. Расчетные усилия указаны в таблице 4. Для верхней части колонны в сечении 1 – 1 М = 517 кН⋅м; N = 394 кН; Q = -320,16 кН; в сечении 2 – 2 при том же сочетании нагрузок (1, 2, 3* 4, 5*) M = 981 кН⋅м. Для нижней части колонны в сечениях 3 – 3 и 4 – 4 М1 = 2697 кН⋅м; N1 = 4154 кН; М2 = 904 кН⋅м; N2 = 1247 кН; Qmax= 1272 кН. Материал колонны – сталь С275, при толщине листового проката t20 мм, Rу=230МПа. В однопролетной раме с жестким сопряжением ригеля с колонной верхний конец колонны закреплен только от поворота. Так как Нв/Нн = 6000/12000 = 0,5 0,6 и Nн/Nв= 4154/394=10,5> 3; и Iв/Iн=0,2 принимаем в = 3, н = 2. Из таблицы 4 в сечениях 1 – 1 и 4 -4 Nв =612 кН, Nн = 672,28кН) Расчетные длины для нижней и верхней частей колонны в плоскости рамы 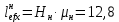 ⋅2=25,6 м; ⋅2=25,6 м; 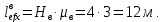 Расчетные длины колонны из плоскости рамы 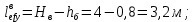 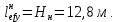 Таблица 7.  |
