Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів
 Скачать 2.54 Mb.
|
7.3 Доповняльний код числаДоповняльний код числа N=0,a1a2..an таке машинне уявлення, в якому число  записується оберненим кодом  із збільшенням в молодшому розряді на +1.Правило перекладу з прямого коду в додатній код наступне: - якщо в знаковому розряді знаходиться (q1) тобто число негативне, то всі цифри числа, окрім розрядів знаків, замінюються вирахуваннями з (q1) значення розряду, а потім до цифри останнього молодшого розряду додається одиниця; - якщо в знаковому розряді знаходиться 0 (або 00) тобто число позитивне, то перетворення цифр не відбувається. Приклади: а) -243476(10); 9\243476(10)пр = 9\756523об + 0000001 = 9\756524(10)доп б) -0111000111(2); 1\0111000111(2)пр.; 1\1000111000(2)об + 0\0000000001(2)= 1\1000111001(2)доп Перевірка: 1\1000111001доп +1\0111000111пр 10.0000000000 (2(10)) в) –0,101110 ; 1\101110пр ; 1\010001об + 0\000001 = 1\010010доп. г) +425736(10); 0\425736(10)пр = 0\425736(10)доп= 0\425736(10)об Таким чином, для позитивних чисел прямий, оберненій і доповняльний коди співпадають, для негативного числа вони різні. Для позитивного числа в розряді знаку завжди встановлюють 0 або 00, а для негативного 1 або 11 (для довільної основи q знак «-»має код (q 1)). Узагальнемо і отримуємо вираз перекладу чисел у доповняльний код: 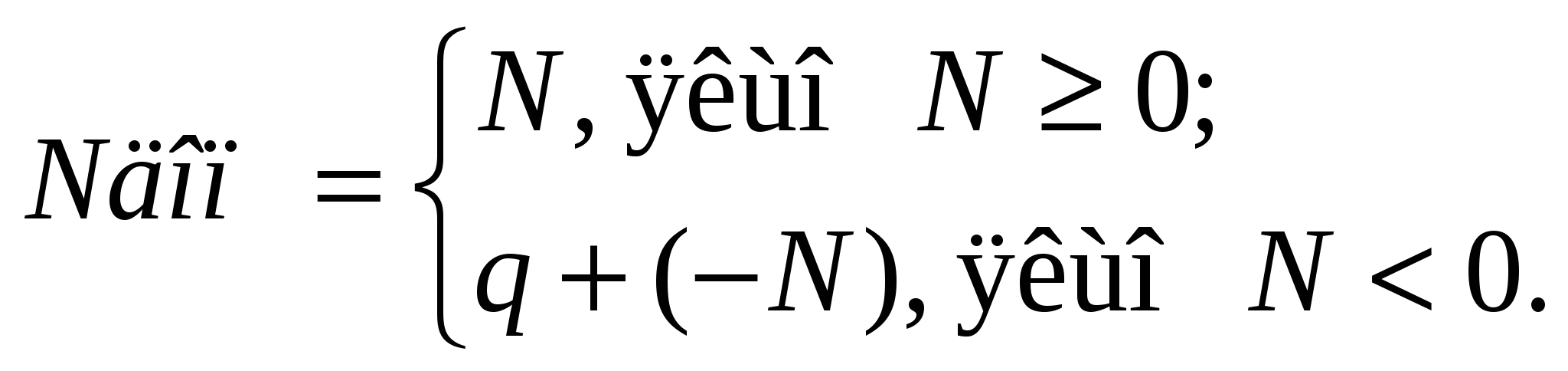 Приклади: а) +0,275936(10); 0\,275936(10) пр= 0\,275936(10)доп (бо позитивне). б) 0,275936(10); 10,000000(10)+(–0,275936(10)) = 9\,724064доп Звідси Nдоп=q+(N), тобто додатній код є математичним доповненням числа до основи системи числення. Покажемо, що доповняльний код – це доповнення до q, тобто:  . Звідси,  враховуючи це, будемо віднімати.Приклад: A = –0,1011; тоді Aдоп = _ 10,0000 0,1011 1\,0101 Отримано доповняльний код. Покажемо, що обернений код – це доповнення до q–q- n, тобто:  , якщо A негативне, то Aоб=q–q-n-|A|. Звідси, треба віднімати з q негативне число і молодшу 1 (тобто q-n).Для довільної основи q це означає, що обернений код числа Аоб порозрядно формується від`ємом значення Апр в і-му розряді від (q-1). Максимальне додатне число, що представляється при цьому дорівнює (1–2-n), або Nmax = 0,111...11 тоді додатній код буде Nдод =1\00... 01. Якщо в наймолодший розряд числа Nmax додати 1 то отримаємо: 1,000...00. Перетворивши це число в додатній код, отримаємо,  тобто: –1 Nдод (1-2-n).7.4 Складання чисел, представлених у формі з фіксованою комою, на двійковому суматорі прямого кодуДвійковим суматором прямого коду (ДСПК) є суматор, в якому відсутній ланцюг порозрядного перенесення між старшим цифровим і знаковим розрядами (рис. 7.3).  Рисунок 7.3 Двійковий суматор прямого коду (ДСПК) На ДСПК можна складати тільки числа, що мають однакові знаки, а результат складання < 1 (для правильних дробів) або менше виразу 2n1 (для цілого числа). Аналіз показує, що такий суматор виконує не всі операції складання, а лише дві з чотирьох: А+В і (А+В). Сигнал пере-повнення Пnстаршого n-розряду служить лише для індикації факту, що воно було, покладаючи подальші турботи на користувача або ЦА, а знак суми C визначається за знаком будь-якого операнда, наприклад SgA (SgB). Нехай задані операнди: 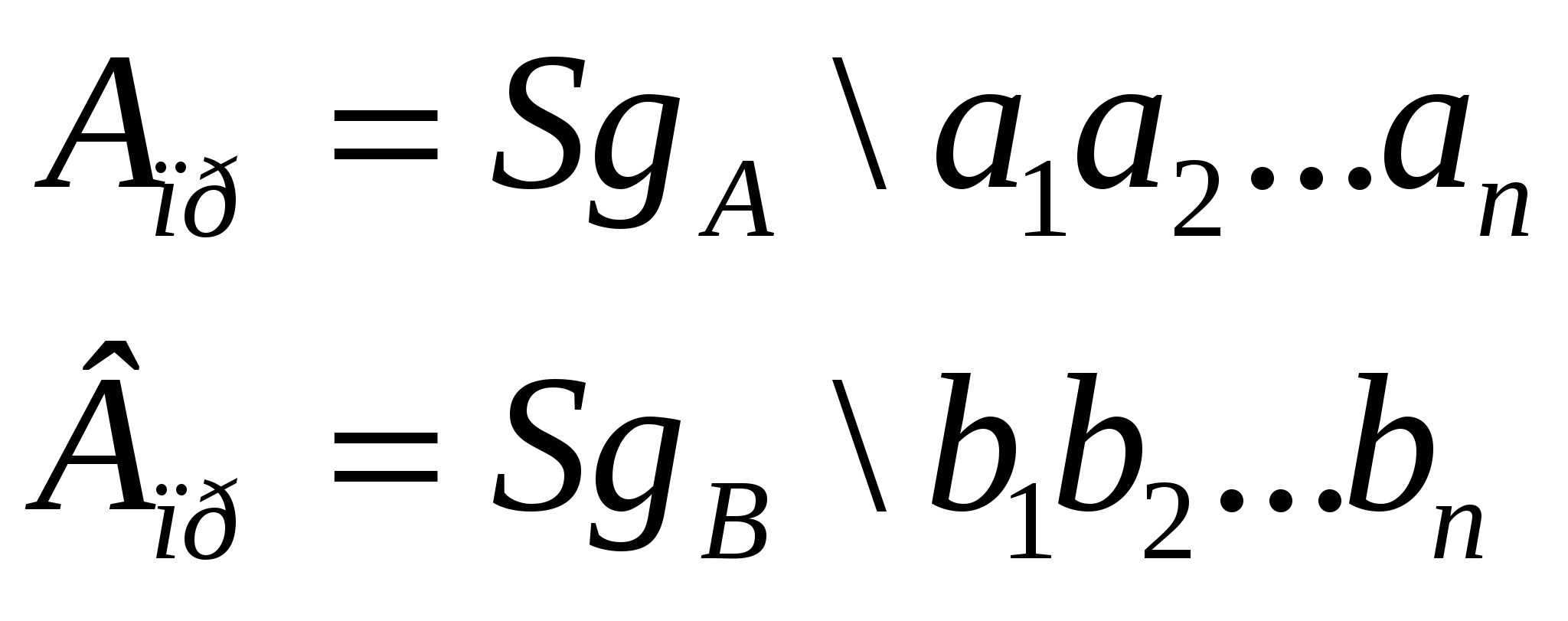 де SgA і SgB – вміст знакових розрядів. Якщо SgA=SgB , то сума чисел матиме знак будь-якого з доданків, а цифрова її частина вийде порозрядним складанням операндів. Приклади. а) Скласти А = 0\1011 (+11); В = 0,0100 (+4). Тут SgA=0; SgB=0 +1011 (+11) 0100 (+4) С = 0\1111 0\1111 (+15) б) Скласти A =0\0101 (-5); B =0\1001 (-9). Тут SgA=1; SgB=1 +0101 (5) 1001 (9) C = 1\1110 1\1110 (14) При складанні чисел на ДСПК можливі випадки, коли абсолютне значення суми операндів перевищує одиницю, тобто має місце переповнення розрядної сітки ЦА. Ознакою переповнення (=1) буде наявність одиниці перенесення Пn із старшого розряду цифрової частини суматора. За цим сигналом повинні відбуватися автоматичний «останов» процесу рахування і коректування масштабних коефіцієнтів операндів А і В з розрахунком, щоб уникнути переповнення (наприклад зміна Кф). |