Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів

• Название: Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів
• Анкор: Ukr1_PTTsA_kl_ch1_10-02-2010.doc
• Дата: 13.02.2018
• Размер: 2.54 Mb.
• Имя файла: Ukr1_PTTsA_kl_ch1_10-02-2010.doc
• Тип: Протокол; #15521
• страница: 10 из 26

7 КОДИ БІНАРНИХ ЧИСЕЛ

7.1 Прямий код числа

Один метод вже розглянуто. Він використовує прямий код числа, 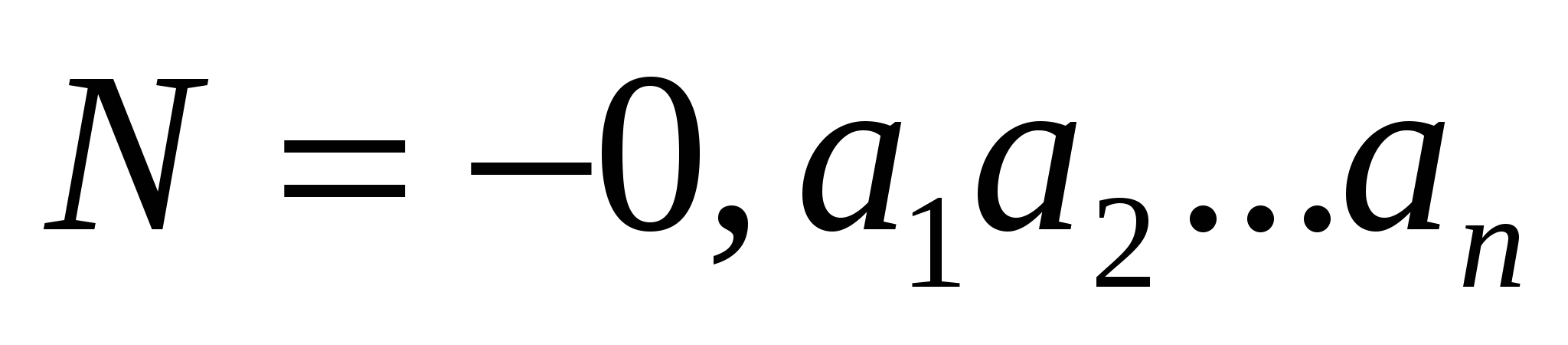(природний запис числа у вигляді правильного дробу), де для машинного його зображення 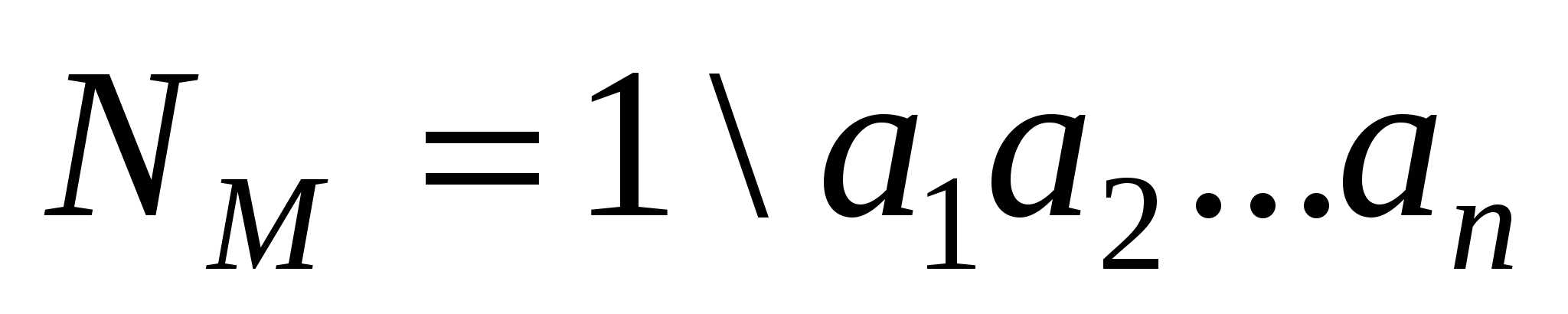використовують 1 (або 11) для позначення знаку «» негативного числа.

Для систем числення з іншою основою q знак «» (мінус) машинного зображення числа кодується старшим зображенням (вісьмирічна 7, шістнадцятирічна F, т.д.).

Прямий код негативного числа є код, всі цифрові розряди якого залишаються незмінними, записаними в нормалізованій формі, а в знаковій частині числа записується "1"(або 11 для модифікованого коду). Наприклад: N =  0,101110 то N_M = 1\101110.

Позитивне число в прямому коді не міняє свого зображення.

Прямий код позитивного числа є код, всі цифрові розряди якого залишаються незмінними (наприклад, записаними в нормалізованій формі), а в знаковій частині числа записується 0 (або 00 для модифікованного коду).

Приклад: N= +0,110101, то N_{M пр}= 0\,110101.

У прямому коді в числову сітку автомата можна записати

,

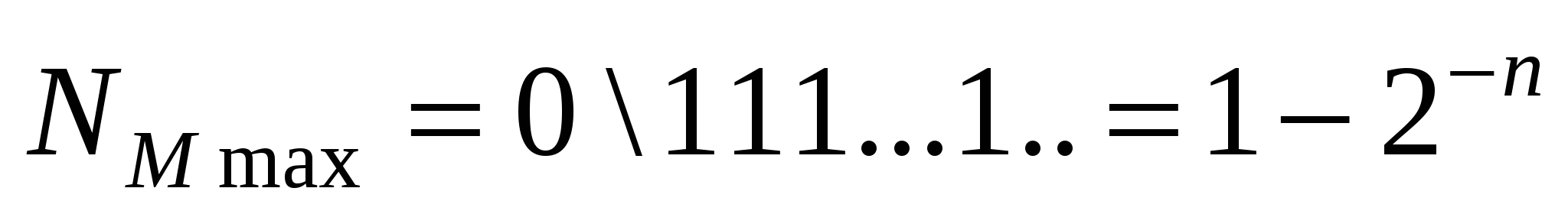де n  кількість розрядів. Діапазон чисел прямого коду (для правильного дробу), лежить в межах, визначених виразом:

_{– (1 – 2-n)  NM  (1 – 2-n), (7.1)}

Але в для операндів А і В в прямому коді виконуються тільки два випадки арифметичні операцій (з чотирьох наявних), тобто:

С_пр= +А_пр+В_пр та С_пр= -А_пр-В_пр = - (А_пр+В_пр).

Іншим методом представлення негативних чисел є уявлення їх в оберненому або доповняльному коді.

7.2 Обернений код числа

Оберненим кодом числа N_M=1\a₁a₂…a_n називається таке машинне зображення числа для якого a_i=0 якщо воно дорівнювало "1" і навпаки, а_i=1, якщо воно дорівнювало "0".

Інакше, оберненим кодом двійкового числа є інверсне зображення цього числа, тобто всі розряди початкового бінарного числа, приймають обернене значення.

Інверсія, інвертування  процедура переходу до протилежного значення розрядів числа в двійковій системі: інверсія «0» дає «1»; інверсія «1» дає «0». Позначається знаком риски ^–(або хвил і, ін.) над числом, його розрядами.

Приклад:N=101110 (природний запис), то N^м_об=1\010001 (машинний запис в оберненому звичайному коді).

Узагальнюючи правила утворення оберненого коду на всі основи систем числення можна вважати, що обернений код негативного числа виходить при відніманні з (q1) цифр по кожному розряду числа за винятком знакових розрядів, які замінюються значенням (q1) тобто:



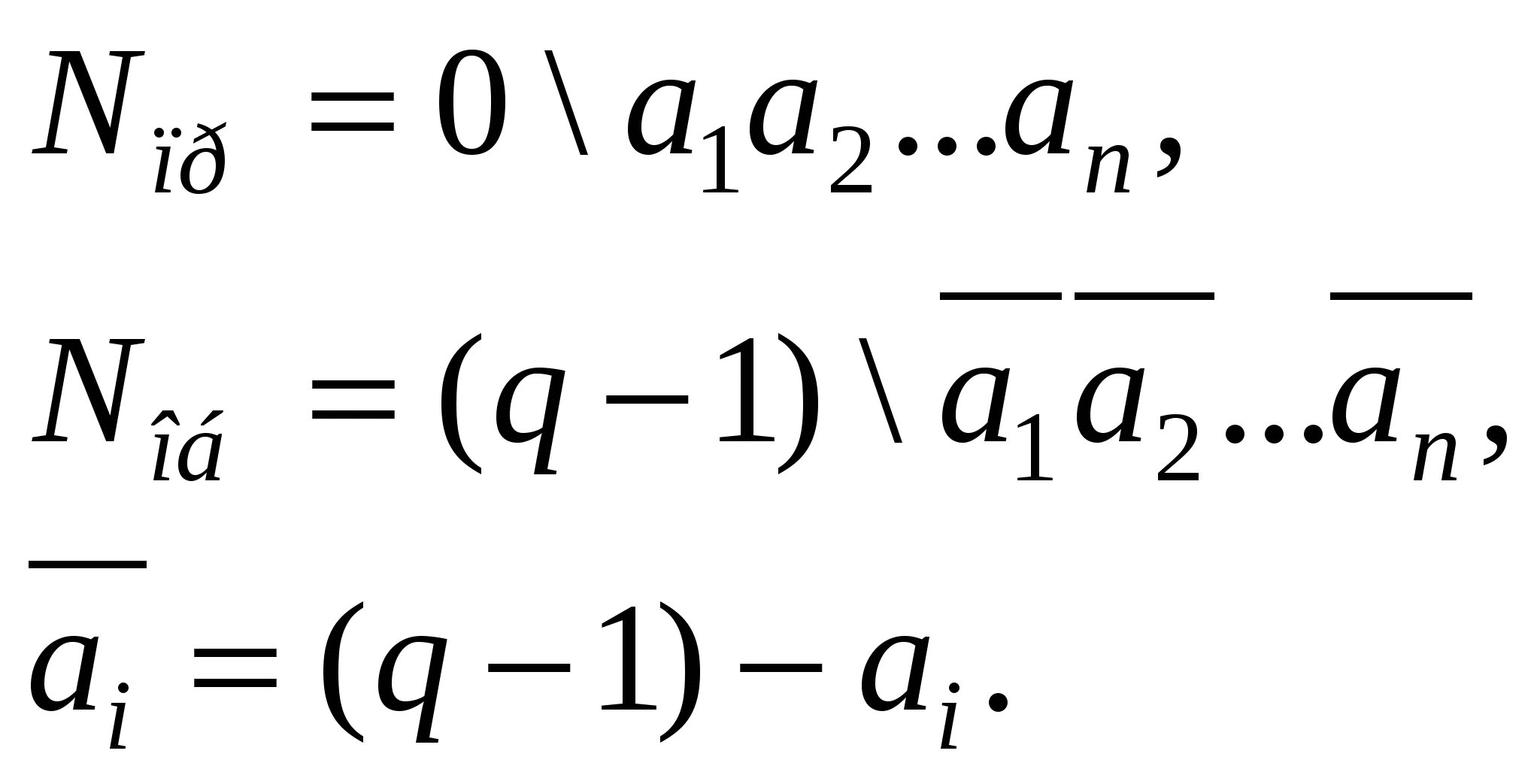
Приклад:  а) 0,286357₍₁₀₎(природний) ↔ 1\,286357_(10)пр (машинний прямий) ↔ 9\,713642_(10)об(машинний обернений).

б) 0,1010111101_(2)пр↔ 1\,0101000010_(2)об

Особливо звернути увагу: якщо в знаковому розряді машинного запису знаходиться (q1)  тобто число негативне, то всі цифри числа, виключаючи знаковий, замінюються вирахуванням з (q1) значення розряду;

якщо в знаковому розряді знаходиться нуль  тобто число позитивне, то перетворення не проводяться.

Приклади: (записи наведено без слеша «\», іноді його може заміняти крапка, кома або інший знак):


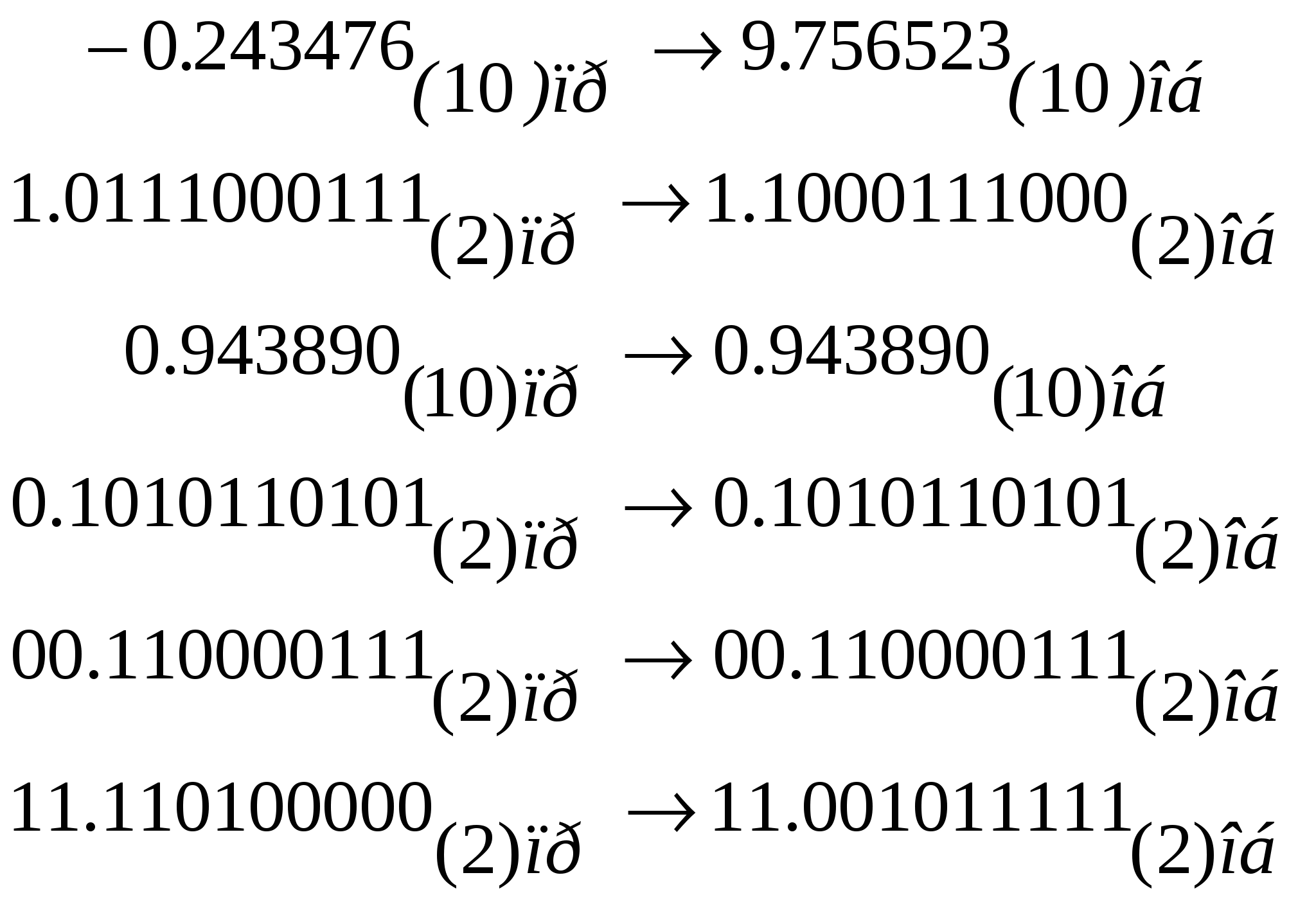
Перехід від оберненого коду до прямого проводиться за аналогічним правилом: із значення (q1) віднімається значення по кожному розряду, окрім знакових (що остаються незмінними).

Для бінарної системи числення (просто щасливий випадок), можна перейти до прямого коду простим інвертуванням розрядів оберненого коду, окрім розрядів знаків.


Приклад:А_об= 11.1100110

А_пр= 11.0011001