Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів
 Скачать 2.54 Mb. Скачать 2.54 Mb.
|
8 АЛГЕБРАЇЧНЕ СКЛАДАННЯ БІНАРНИХ ЧИСЕЛ8.1 Складання чисел на двійковому суматорі доповняльного кодуДвійковим суматором доповняльного коду (ДСДК) називається суматор, що оперує числами, що представлені в доповняльному коді. Основною особливістю ДСДК є наявність ланцюга перенесення одиниці переповнення Пn зі старшого розряду цифрової частини в знаковий розряд (рис. 8.1) і відсутність зворотнього зв’язку перенесення одиниці переповнення ПSg із знакового розряду в наймолодший розряд числа.  Рисунок 8.1 Двійковий суматор доповняльного коду (ДСДК) Для визначення правил складання чисел в ДСДК розглянемо наступну теорему: якщо результат суми доповняльних кодів чисел негативний, то він представлений у доповняльному коді. При доведенні теореми, припускаємо, що числа представлені у формі з фіксованою комою, що стоїть перед старшим розрядом. Розглянемо наступні випадки (всі числа є цілими): Випадок 1. A>0, B>0, а A+B<1 числа позитивні і немає переповнення. Для цього випадку Aдоп =А, Вдоп=В, то Адоп+Вдоп=А+В=[A+B]доп результат позитивний. Покажемо це на прикладі: А = +0,1010; В = +0,0100. 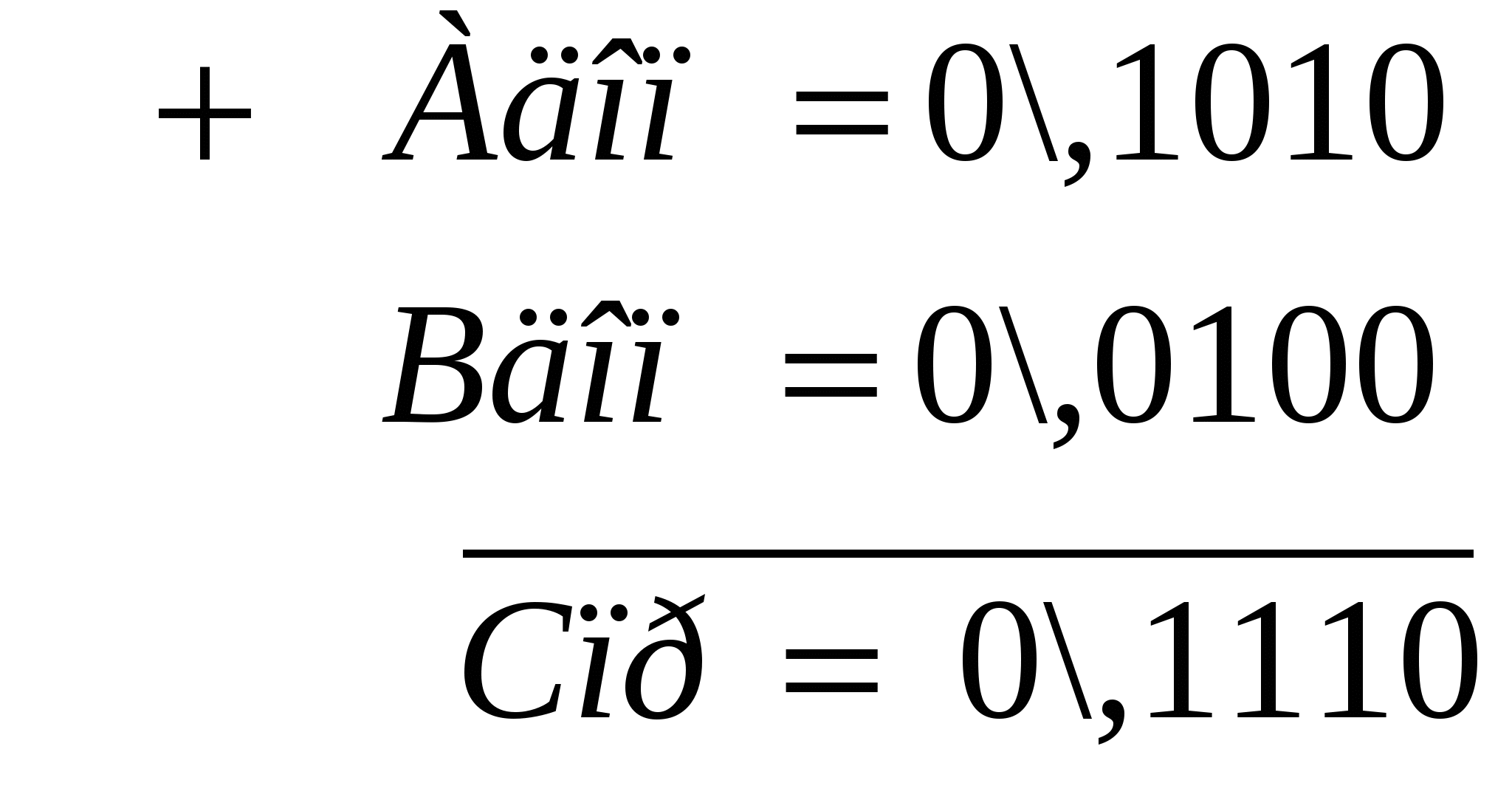 С=+0,1110. С=+0,1110.Випадок 2. A<0, B>0, а |A|B. Для цього випадку Адоп=q+|A |, Вдоп=В; тоді Адоп+Вдоп=q+|A|+B=[A+B]доп – результат негативний. А=0,1011; В=+0,0100 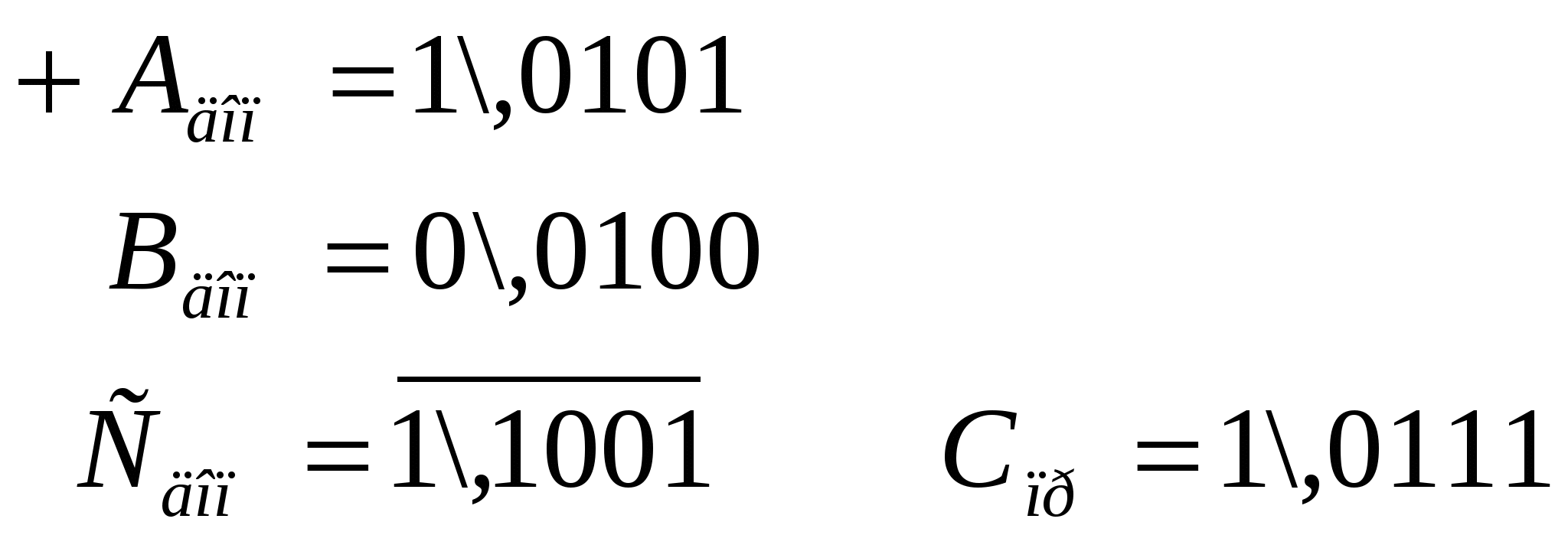 С= - 0,0111. С= - 0,0111.Отриманий результат негативний, це означає, що він представлений у доповняльному коді, і його необхідно перевести в прямий, щоб отримати дійсний результат. Переклад числа з доповняльного коду в прямий здійснюємо за наступним алгоритмом: усі розряди числа (окрім знакових) інвертуються (тобто береться обернений код результату) і в молодший розряд додається 1. Знак суми С зберігається. Випадок 3. A<0, B>0, а |A|<B. для цього випадку Адоп=q+|A|, Вдоп=В; тоді Адоп+Вдоп=q+|A|+B. Оскільки значення цієї суми більше q, то з’являється одиниця перенесення в знаковий розряд, що дорівнює вилученню з суми q одиниці, тобто результат: Адоп+Вдоп=А+В=Спр. Приклад. А =0,0100; В =+0,1011. 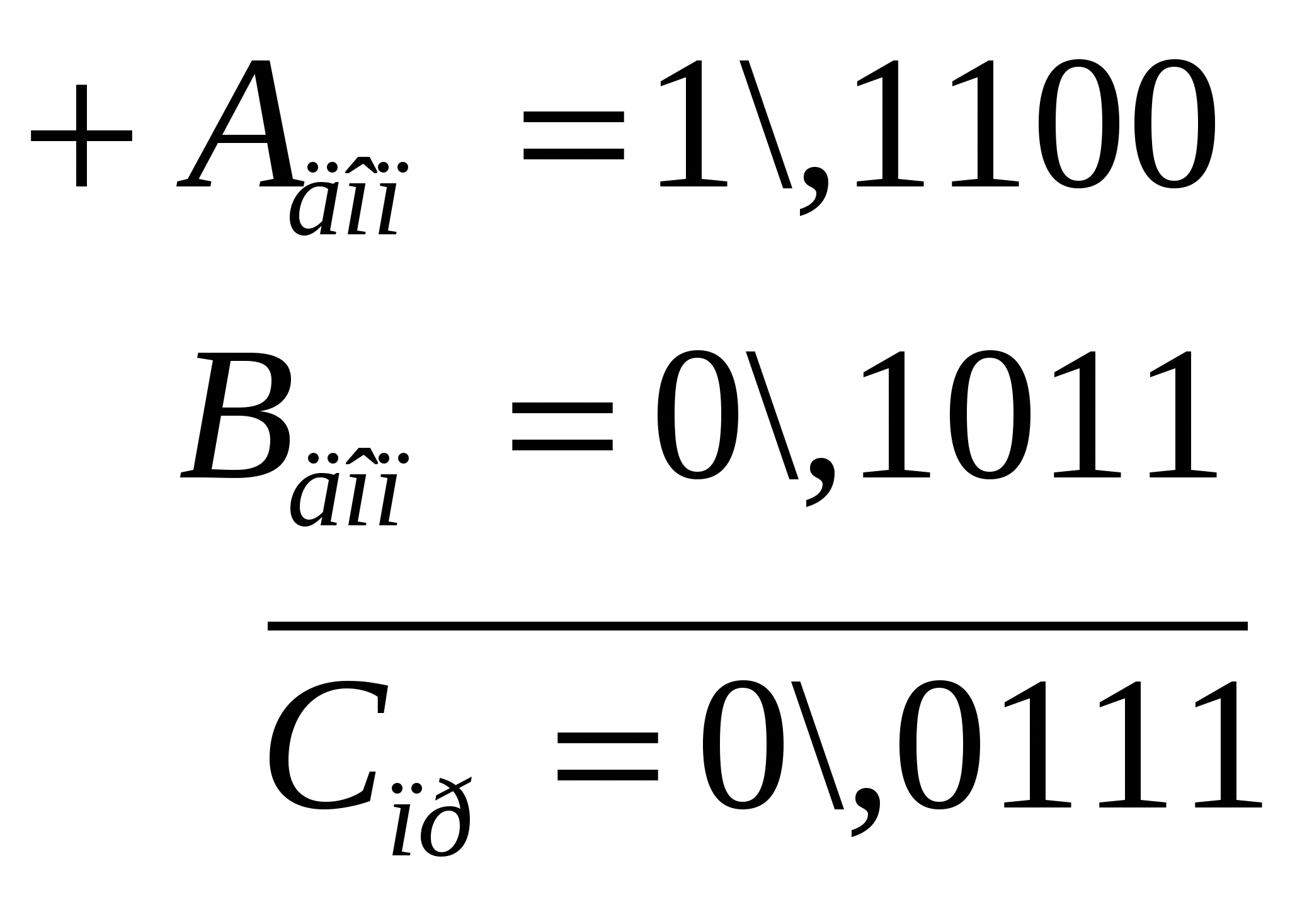 С= + 0,0111. С= + 0,0111.Випадок 4. A<0, B<0, а |A+B|<1. Для цього випадку Адоп=q+(А); Вдоп= q+(В), тоді Адоп+Вдоп=q+(A)+q+(B)=[A+B]доп результат негативний і з’явиться одиниця перенесення із знакового розряду. Приклад. А = 0,0100; В = 0,1011. 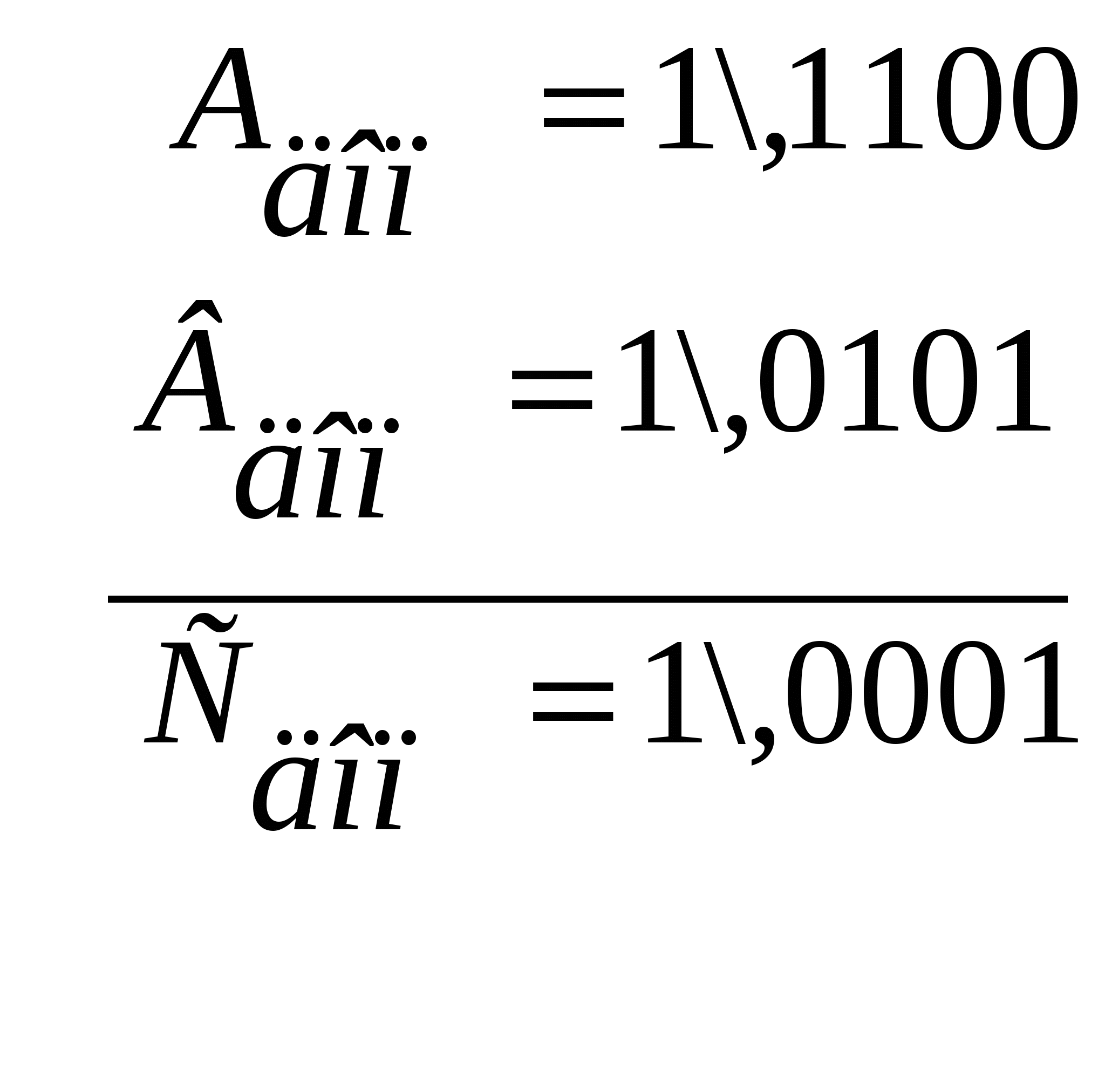 Спр=1\,1111. С= -0,1111 Спр=1\,1111. С= -0,1111Висновок. Теорема справедлива для всіх випадків, в яких не виникає переповнення розрядної сітки, що дозволяє складати в ДСДК машинні зображення чисел за правилами двійкової арифметики. Приклади: Випадок 1. A>0, B>0, C<1. а) A(10) = +0,372914(10)пр; В(10) = +0,564019пр Адоп = 0\,372914 +Вдоп = 0\,564019 Сдоп = 0\,936933 = Спр б) Для цілих чисел: Апр= 0\1001110101 (+629) Впр=0\0101110011(+371) Адоп= 0\1001110101 + Вдоп= 0\0101110011 Сдоп = 0\1111101000 =Спр 1000(10) Перевірка: 629+371=1000 Випадок 2. A>0, B>0, C1 (переповнення розрядової сітки): П Апр=0\672914(10), Впр=0\564019(10). Адоп = 0\672914 +Вдоп= 0\564019 Сдоп=1\236933→0\1236933 (проведено зсув вправо мантиси на один розряд та відновлено знак суми) оПоява в знаковому розряді одиниці позитивного переповнення говорить про переривання роботи для зміни KФ або зсув мантиси вправо на один розряд, а до порядку результату додається одиниця (тобто проводиться нормалізація результату). Апр = 0\1101110101 Впр = 0\0101110011 Адоп = 0\1101110101 + Вдоп = 0\0101110011 Сдоп = 1\0011101000 (далі зсув вправо на один розряд) Спр= 0\10011101000. Перевірка: +885 + 371 =1256 Відбулося переповнення (=1), тобто в знаковому розряді SgС0 з’явилася ознака (1). Що це? ЦА не може розібрати ситуацію, це знак «мінус» суми С або ознака переповнення. Для вирішення цього треба в поле знаків додати ще один розряд (використовується модифікований доповняльний код, див. гл. 9). Зсув вправо (вліво) числа зменшує (збільшує) його на порядок: тобто змінеться Кф (для ФФК) або порядок Р (для ФРК) і цю зміну треба відкорегувати, щоб значення числа не змінилось. Випадок 3. A>0, B<0, |A|>|B|: тобто C =A+q+B оскільки C>q, то qповинне бути відібране, що робиться шляхом відкидання сигналу перенесення, що виникає в знаковому розряді. A(10)пр=+0.732904; В(10)пр= -0.042703(зрівняно кількість розрядів А і В), В(10)доп=9\,957297 [А]доп= 0\,732904 + [В]доп= 9\,957297 [С]доп=10\,690201; Спр= +0,690201. При цьому в ДСДК переповнення 1 розряду SgC не використовується (відкидається). При визначенні доповняльного коду В(10)доп, спочатку провели вирівнювання розрядності чисел, додавши 0 в старший розряд числа Впр, а потім віднімали з (q1)=9 значення по кожному розряду і отримали обернений код, потім до його молодшого розряду додали 1. Розглянемо ще приклад: А(2)пр=0\1101110101 (+885); В(2)пр =1\0110110101 (437). + Адоп= 0\1101110101 Вдоп = 1\1001001011 Сдоп=10\0111000000 Спр = 0\0111000000 (+448) Одиниця переповнення 1 відкидається (бо ДСДК), знак результату С позитивний і означає прямий код. В а) A(10)пр = +0,324761 В(10)пр = -0,560129 + Адоп = 0\,324761 Вдоп= 9\,439871 Сдоп = 9\,764632 ; Спр = 9\,235368 б) А(2)пр = 0\0110011001 (+409); В(2)пр = 1\1010011101 (669). + Адоп= 0\0110011001 Вдоп = 1\0101100011 Сдоп = 1\1011111100 Необхідно перетворення в прямий код, тому що результат суми від’ємний. Соб =1\0100000011 Інверсний (обернений) код результату. Далі в молодший розряд додаємо 1, тобто +0\0000000001. Тоді Спр=1\0100000100 = 260(10); (Формат числа надан в ФФЗ. При представленні його в ФРК необхідна буде нормалізація Спр: представлення мантиси у вигляді правильного дробу з зсувом вліво на 10розрядів і відповідним корегуванням значення порядку Р на +10, а потім зсув вліво на 1 розряд, бо маємо 0 після коми, а далі корекція порядку на -1). Спр = 1\100000100. Перевірка: 669+409 =260 ипадок 4. A>0, B<0, |A|<|B|, C =A+q+B, оскільки C<0, то C=q+(A+B). Випадок 5. A<0, B<0, |A|+|B|<1, C=q+A+q+B<0. При цьому, одна основа повинна бути відкинута за рахунок втрати сигналу перенесення в знаковому розряді. Тоді C=q+(A+B). В A(10)пр = -0,432096 В(10)пр = -0,392671 + Адоп = 9\,567904 Вдоп = 9\,607329 Сдоп =19\,175233 Спр= 9\,824767 Переповнення1в знаковому розряді пропадає, оскільки використовується ДСДК. ипадок 6. A<0, B<0, але |A|+|B|>0. Це також випадок переповнення розрядної сітки, але на відміну від випадку 2 переповнення тут негативне. A(10)пр = -0,610892(10); В(10)пр = -0,843507(10) Адоп = 9\,389108 + Вдоп = 9\,156493 Сдоп =18\,545601 Поява цифри 8 в знаковому розряді говорить про те, що відбулося переповнення SgС0, необхідний зсув вправо з відновленням знаку і перетворення результату в прямий код. Сдоп=18\,545601; після зсуву Сдоп=9\,8545601 (проведено зсув на 1 розряд вправо і відновлення знаку), Спр=9\,1454399. Розглянемо приклад в двійковій системі числення. Апр = -1101110100; Впр = -1110111010 Адоп = 1\0010001100 + Вдоп = 1\0001000110 Сдоп =10\0011010010 Було переповнення. Необхідний зсув вправо, для відновлення знаку з подальшим перетворенням результату в прямий код. Сдоп =10\0011010010=1\00011010010; Спр=1\11100101110. Перевірка: 884954= 1838. У звичайному доповняльному коді є проблема із зображенням числа «1». Тут розглядають два варіанти: 1. Виробляти сигнал переповнення, якщо в знаковому розряді (q1), а в цифрових розрядах є нулі тобто Адоп= 1.0000…0. 2. Вважати 1 допустимим значенням, але при цьому її зображення в прямому коді співпадатиме із зображенням у доповняльному коді. 1(10)доп = 9.00000…0 = 9.99999…9 + 0.0000…01 = 9.00000…0 = 1(10)пр 1(2)доп = 1.00000…0 = 1.11111…1 + 0.0000…01 = 1(2)пр Щоб відрізняти 1 від +1, використовують модифікований доповняльний код (див. розділ 9). |
