Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів

• Название: Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів
• Анкор: Ukr1_PTTsA_kl_ch1_10-02-2010.doc
• Дата: 13.02.2018
• Размер: 2.54 Mb.
• Имя файла: Ukr1_PTTsA_kl_ch1_10-02-2010.doc
• Тип: Протокол; #15521
• страница: 9 из 26

5.3 Погрішності представлення чисел

Представлення чисел в ЦА, як ми бачимо, завжди спричиняє за собою появу погрішностей в розрахунках, величина яких залежить від обмежень, що накладаються на автомат по розрядній сітці та формі представлення чисел.

5.3.1 Абсолютна похибка представлення чисел N

Абсолютна похибка представлення чисел Nназивається різниця між дійсним значенням числа N_і та його значенням N_m, отриманим після машинного відображення, операцій АЛП.

Приклад: двійкове число +11,00111000111 при n=15 і K_Ф=2^k, k=6, тоді N_m = 0\000011,001110001 [останні два розряди 11  втрачені]. Перевівши в десяткові числа, отримаємо:

N =11,00111000111 (+3,2221678);

N_m =0\000011,001110001 (+3,2207031);

N =N–N_m = +3,2221678– (+3,2207031)= +0,0014647.

Правило. Максимальна похибка N для чисел формату з фіксованою комою не перевищує одиниці молодшого розряду сітки:

_,

де n  розрядність автомата;

k  степінь масштабного коефіцієнта К_Ф;

N_m  значення машинного числа в двійковій системі після його переводу (тобто з N в N_m).

5.3.2 Відносна похибка представлення числа N

Відносна похибка представлення числа N. Це відношення абсолютної погрішності N до числа N в процентному відношенні, тобто: .

Зазвичай N визначається математично після виконання арифметичних операцій в десятковій системі.

Після визначення абсолютної погрішності визначаємо відносну похибку в %. Приклад: з попереднього рішення N=0,0014647, тоді

6 БІНАРНА (ДВІЙКОВА) АРИФМЕТИКА

У арифметиці будь-якого типу беруть участь завжди два або більше чисел. Як результат виконання арифметичних операцій з’являється нове число. Формально це можна представити у вигляді:

_{, (6.1)}

де  знак будь-якої арифметичної дії з чотирьох: складання, віднімання, множення, ділення.

Будь-яке з чисел А, B₀, B₁, B_n є операндами, тобто числами, що беруть участь в арифметичних операціях, які виконуються ЦА.

Необхідно звернути увагу на те, що у виразі 6.1 опущено індекс m  машинне число. Але всі операнди і результат С є машинними числами. Правила виконання арифметичних операцій на рівні розрядів операндів:

,

,

,

де n  розрядна сітка автомата.

Алгоритми виконання арифметичних операцій в системі числення з основою q аналогічні алгоритмам в десятковій системі числення.

Результат виконання операції  цифр а_i та b_i в i-м розряді представляється двома цифрами: цифрою C_i  результатом відповідної операції в даному розряді та цифрою П_i  перенесенням в старший розряд або позики зі старшого розряду (при відніманні).

Результат C_i і перенесення П_iформуються за наступними правилами:

Додавання: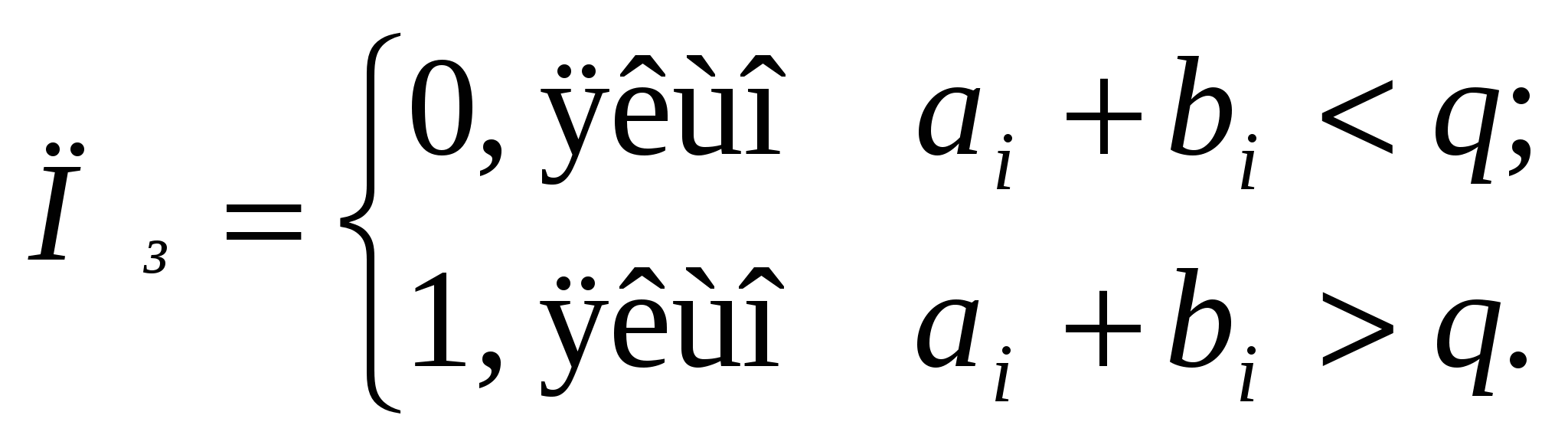





Віднімання: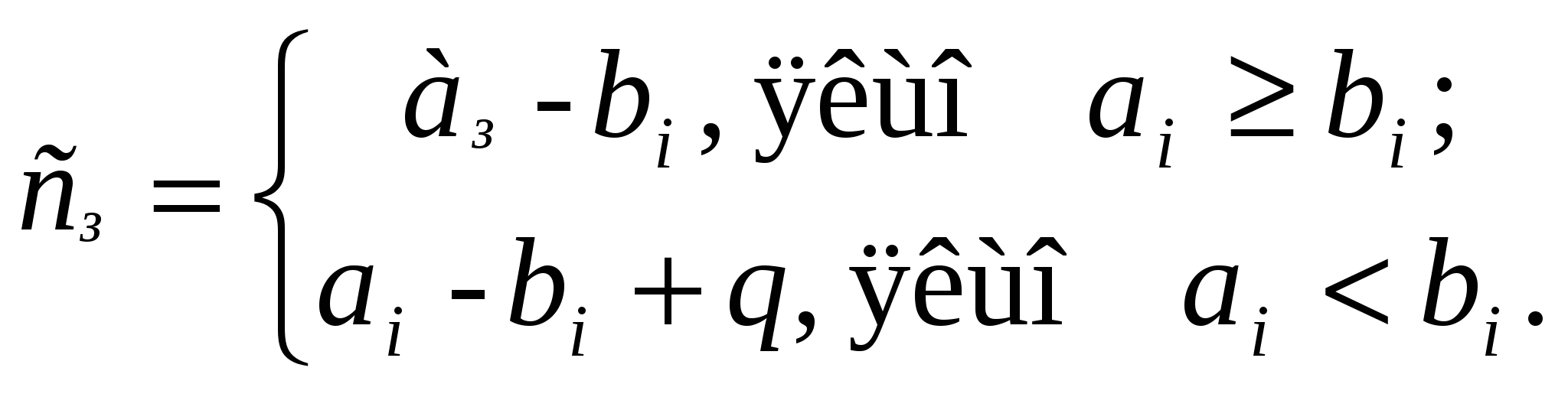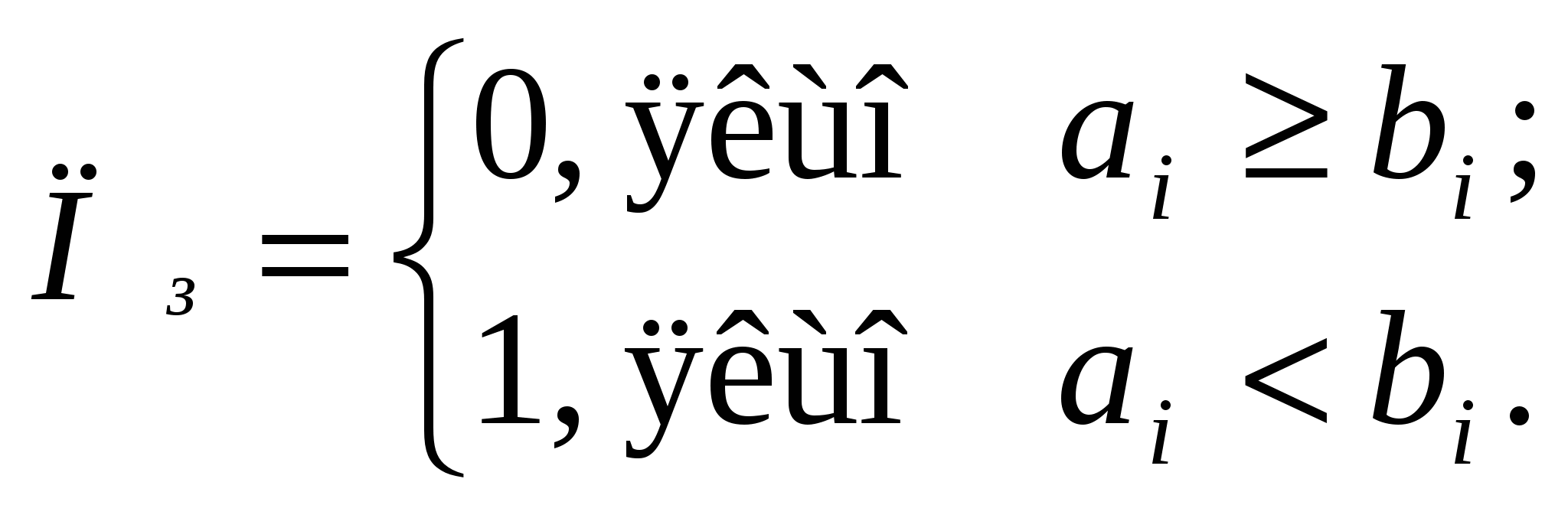





Множення: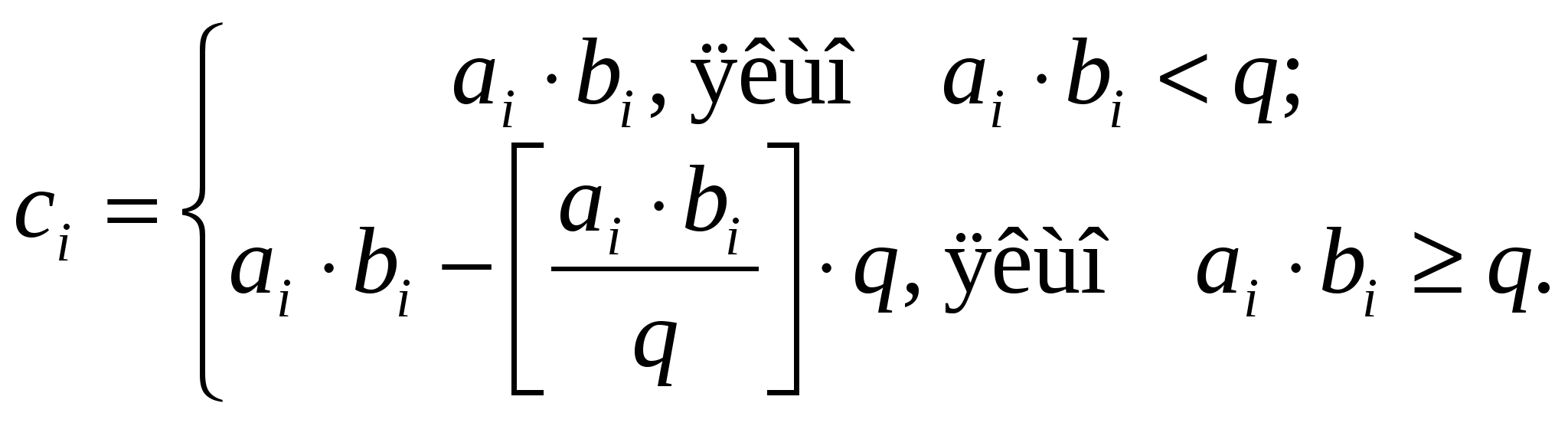
Виконання операції не може бути зведене до операції над окремими цифрами розрядів. Тому ділення виконується по аналогії з діленням в десятковій системі.

Двійковий напівсуматор (HS) пристрій, що виконує арифметичну дію складання без урахування переносу П_iз попереднього розряду, тобто на його вхід подаються тільки числа розрядів a_i та b_i без переносу П_i (наприклад, наймолодші розряди операндів А і В).



Рисунок 6.1  Двійковий напівсуматор

Правила складання напівсуматора можна представити у вигляді таблиці 6.1, що має назву таблиця істинності (ТІ).

Таблиця 6.1  Напівсуматор

ai	bi	ci	Пi
0 0 1 1	0 1 0 1	0 1 1 0	0 0 0 1

Тут порозрядне складання виконується за формулою:

_{ai + bi = Ci + Пi ,}

де а_i, b_i  розряди чисел А, В;

C_i  сума і-го розряду;

П_i  перенос у наступний розряд.

Але не враховувати переносів при складанні багаторозрядних чисел не можна. Тому, при складанні користуються пристроєм, що має назву двійковий суматор. Це пристрій, що виконує арифметичні дії складання з урахуванням переносу (П_i-1).від попереднього розряду і передачі переносу (П_i). в наступний розряд. Його робота і структурна схема була розглянута в розділі 3 (рис. 3.3).

ТІ двійкового суматора представлена в таблиці 6.2.

Таблиця 6.2  Суматор

ai	bi	П(i-1)	Ci	Пi
0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 0 0 0 1 1 1 1	0 1 1 0 1 0 0 1	0 0 0 1 0 1 1 1

Тут порозрядне складання виконується за формулою:

_{ai+bi+Пi-1=Ci+Пi,}

де а_i, b_i  розряди чисел А, В;

C_i  сума і-го розряду;

П_i-1  перенос з попереднього розряду;

П_i  перенос у наступний розряд.

При виконанні арифметичної операції віднімання в двійковій системі числення (в десятковій аналогічно), нерідко проводиться позика, рівно-сильна відніманню одиниці зі старшого розряду. Запозичення зі старшого розряду еквівалентно додаванню до молодшого розряду величини основи.

Крім того, цю позику необхідно враховувати при відніманні цифр наступного старшого розряду (тобто чи була позика в молодшому розряді). З урахуванням цього, і пам’ятаючи, що від’ємник завжди повинен бути менше зменшуваного можна представити правила у вигляді таблиці 6.3.

Таблиця 6.3 – Від’ємник бінарних чисел

ai	bi	Zi	Ci	Z(i+1)
0 1 1 0 0 1 1 0	0 0 1 1 0 0 1 1	0 0 0 0 -1 -1 -1 -1	0 1 0 1 1 0 1 0	0 0 0 -1 -1 0 -1 -1

Порозрядне віднімання виконується за формулою:

а_i – b_i+ Z_i = C_i+ Z_i+1,

де a_i, b_i – операнди розряду;

C_i– різниця розряду;

Z_i– позика із молодшого і-го розряду;

Z_i+1 – позика у старшого розряду.
Порівняння даних табл. 6.2 і 6.3 свідчать про те, що при відніманні операнду В від А порозрядно АЛП повинен мати додаткові розряди для зберігання знаку «–» для Z_i , Z_(i+1) що ускладнює схему АЛП (при тому що a_i, b_i і С мають знак «+»). Тому перевагу надано двійковому суматору.

Розглянемо приклади на складання і віднімання для чисел з фіксованою комою (ФФК). Оперуватимемо з шестизначними, позитивними числами за модулем менше одиниці.

Приклади: а) виконати операцію складання бінарних чисел +А і +В (двох операндів А і В):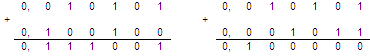



б) виконати операцію віднімання бінарних чисел +С і D (двох операндів С і D):



в) віднімання в 8-ій системі: г) віднімання в 3-ій системі: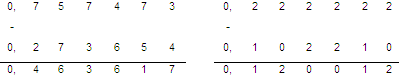



д) виконати операцію множення бінарних чисел +Е і +F:



е) виконати ділення бінарних чисел +G і +H (у вигляді неправильного дробу +G і цілого числа +H):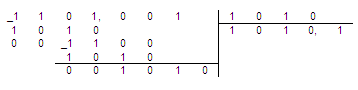



Проте, таке віднімання, ділення і множення для автоматів є складним оскільки при виконанні цих операцій в обчислювальних ЦА виникає проблема представлення негативних чисел. Для машинного представлення негативних чисел використовують коди: прямий, обернений і доповняльний.

Одним із способів виконання операцій за допомогою двійкового суматора, є заміна операції віднімання операцією суми із оберненим або доповняльним кодом негативного числа:

_{А–В= А + (В)=А+В*.}

Заміна віднімання складанням ставить проблему представлення негативного числа в цифровому форматі. Це може бути вирішєно, наприклад, за допомогою використання властивості циклічності чисел при їх переліку, рахунку, зображенні (два, три, …, дванадцять, тринадцять…).