Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів

• Название: Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів
• Анкор: Ukr1_PTTsA_kl_ch1_10-02-2010.doc
• Дата: 13.02.2018
• Размер: 2.54 Mb.
• Имя файла: Ukr1_PTTsA_kl_ch1_10-02-2010.doc
• Тип: Протокол; #15521
• страница: 5 из 26

3.2 Вибір системи числення комп’ютера

3.2.1 Переваги двійкової системи

Розробку комп’ютера починають з вибору системи числення, методів виконання арифметичних і логічних операцій, елементної бази. Ці питання є важливими, оскільки повинні забезпечити задану точність і швидкість обчислень, надійність в роботі, діапазон чисел.

Вибір системи числення у великій мірі обумовлюється наступними основними причинами:

1. Основу системи визначає число знаків (їх зображень) в одному розряді. Тут перевагу має двійкова система, а не десяткова оскільки вона вимагає всього два знаки (стани), а десяткова  десять. Елементи, з десятьма станами (декатрони), що є в наш час, мають малу швидкість перемикання, громіздкі, мають невисоку надійність в роботі.

2. З одного боку система числень повинна забезпечити простоту арифметичних операцій, а з іншого великий діапазон уявних чисел. Ці дві суперечності вирішуються на користь простоти арифметичних операцій при представленні чисел. Насправді, в двійковій системі не треба додаткових пристроїв представлення чисел. Сам сигнал несе інформацію про число і має двійкову природу: є сигнал або його немає - "1 " або "0". Крім того, майже всі елементи електронних схем (є струм/ напруга або ні) мають двійкову природу (реле, діод, транзистор, тригер, фотоприймач, стан оптоволокна, ін.).

Якщо прийняти показник ефективності системи з погляду витрат устаткування:



де q  основа (глибина) системи, n – довжина (розрядність) системи.

Розрядність n визначається з діапазону уявних чисел. Максимальне число з основою q: звідси знайдемо n:

n=log_q( N_(q)max + 1),

тоді витрати на устаткування підраховують за формулою:

_{C = q logq (N(q) max + 1).}

Якщо за одиницю устаткування прийняти умовний елемент з одним стійким станом, то можна порівняти системи числення з погляду витрат.

Графік відносного показника приведений на рис. 3.2.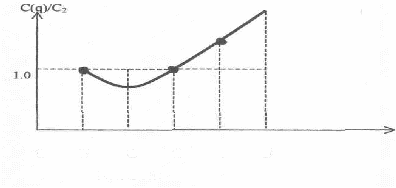



Рисунок 3.2  Відносні витрати при різних значеннях основ

Наймінімальніші витрати будуть при основі е = 2,72, тобто, з погляду витрат, виходить найекономнішою буде система з q=3. Вона застосовується в ЕОМ "Сетунь". Проте, більшість ЕОМ використовують двійкову системи через простоту арифметичних операцій в ній.

Розглянемо це на прикладі складання в цій системі:

0+0=0, 1+0=1, 0+1=1, 1+1=10.

Складання цілих чисел без знаку представлено схемою (рис. 3.3).

Приклад. Знайти С=А+В. А=+1011 (+11); В=+1001 (+9); С=+10100 (+20).

Рисунок 3.3  Структурна схема бінарного (двійкового) суматора
Множення проводиться в двійковій системі ще простіше: 00=0, 01=0, 10=0, 11=1.

4 МЕТОДИ ПЕРЕКЛАДУ ЧИСЕЛ З ОДНІЄЇ ПОЗИЦІЙНОЇ СИСТЕМИ ЧИСЛЕННЯ В ІНШУ

Раніше ми відзначали, що будь-яке число можна представити поліномом з основою q₁, але це ж число можна представити іншим поліномом (див. рис. 3.3) з основою q₂, інакше: N(q₁)= N(q₂). Представимо це для загального числа (що має цілу і дрібну частини  неправильний дріб) у наступному вигляді: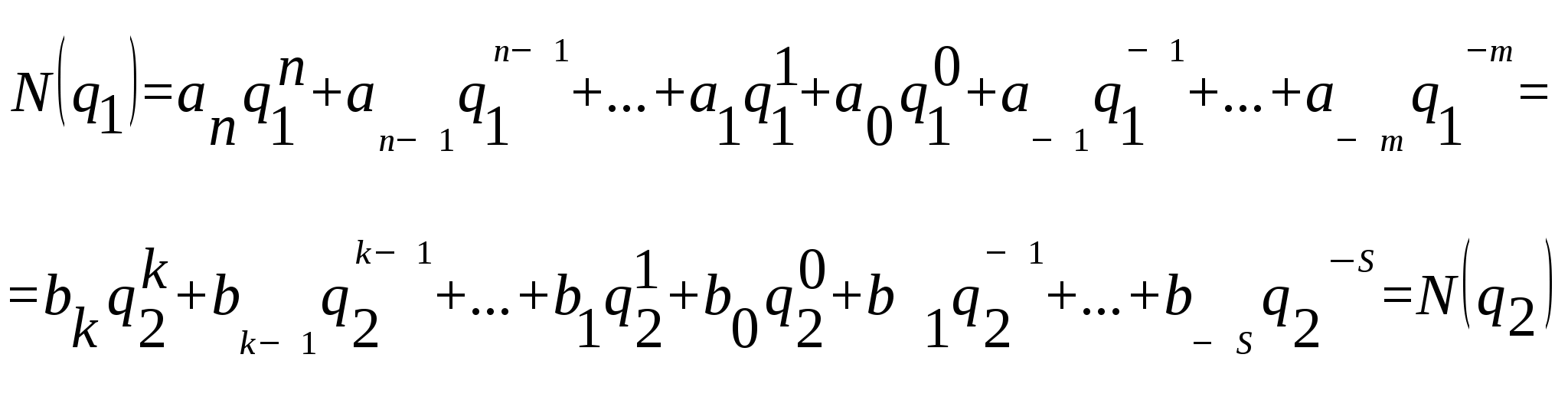

4.1 Методи перекладу цілих чисел

4.1.1 Метод підбору коефіцієнтів

Завдання перекладу числа з основою q₁ в число з основою q₂ зводиться до відшукування коефіцієнтів полінома нової основи. Цю задачу можна вирішити методом підбору коефіцієнтів полінома.

Правило. На початку беремо число з максимальною степінню основи, перевіряємо її вхід до даного числа так, щоб воно не перевищувало задане, потім підбираємо коефіцієнти менших степіней полінома, так щоб сума давала початкове число. Всі дії повинні виконуватися за правилами q_і-ї арифметики, тобто за правилами початкової системи числення.

Наприклад. Перевести десяткове число 96 у трійкову систему.

Рішення. 96 = 03⁵+13⁴ + 03³+13²+23¹ + 03⁰ = 010120₍₃₎

Проведемо перевірку методом підстановки значень ваги розрядів, множення його на підібраний коефіцієнт і обчислення загальної суми.

96=0243 + 181 + 027 + 19 +23 + 01.

Цей прийом застосовується тільки при "ручних" перекладах. Машинні алгоритми використовують метод ділення на основу нової системи числення.

4.1.2 Метод ділення на основу нової системи

Поліном цілого числа N(q₁) можна записати за схемою Горнера в іншому вигляді:



де b₀…b_k -коефіцієнти молодшого b₀, старшого b_k розрядів числа N(q₂).

Якщо праву частину розділити на q₂, то отримаємо цілу частину (у лапках) і залишок з b_і (0k). Повторюючи ділення k+1 разів отримуємо кожного разу залишки b₁, b₂, ..., b_к і цілі частини. Останній залишок b_к є старшим розрядом залишку числа, представленого в основі q₂ (неподільний залишок).

Приклад. 12₍₁₀₎ перевести в бінарну (двійкову) систему числення.

Рішення. Ділимо на q=2 (у дужки поміщений залишок):


12:2=6(0)

6 : 2=3(0)

3 : 2=1(1)

Частка (1) менше основи 2, тому це теж залишок, причому старший, тому припиняємо ділення. Відповідь: 1100 (12₍₁₀₎).

4.1.3 Метод ділення на основу в будь-якій позитивній степіні

Попередній метод має один недолік. При великих числах, операція ділення має багато ітерацій. Це знижує швидкодію. Метод ділення на основу нової системи в будь-якому позитивному степіні аналогічний попередньому. Тут беруть для ділення число (з новою основою q_k) близьке до заданого числа N(q_i), але що не перевищує його. Кожен залишок від ділення записують в двійкових розрядах, число яких рівне узятому степіні.

Наприклад. Перевести в бінарну систему числення число N=523 _(10).

Рішення. Вибираємо, найближче до заданого, число 2⁹ = 512 і ділимо:

523 : 512=1(залишок 11).

Отримали два залишки: старший  1, молодший  11. Кожний із залишків розписуємо в дев’яти бінарних розрядах: 1000000000 і 000001011. Потім сполучаємо (додаємо) записи (старші нулі можна не записувати) і отримуємо результат- число 1000001011.

В двійковій системі (для цілого числа) b₀ завжди «0» або «1». В першому випадку N(q₂)  це парне число, в другому  непарне.

4.1.4 Метод віднімання найближчих, менших степінних ваг

Метод полягає в наступному. Вибирають значення найближчої, розрядної ваги бінарного (двійкового) числа, менше заданого.

Віднімаючи його від заданого числа, отримують залишок. У розряді вибраної ваги, ставиться 1. Потім порівнюють залишок з новим меншим ваговим розрядом. Якщо залишок менший, то в цьому ваговому розряді ставиться 0, якщо залишок більший, то в цьому розряді ставиться 1, а із залишку віднімається вага цього розряду. Виходить новий залишок, який знову порівнюється з наступними меншими вагами. Так продовжується до останнього (молодшого) вагового бінарного розряду і отримають число.

Приклад. Перевести десяткове число 1125 в двійкове. Метод  віднімання менших найближчих розрядних ваг. Найближчою меншою розрядною вагою буде число 1024=2¹⁰. Ставимо в десятому розряді 1 (зліва від коми, де міститься 2¹⁰).

Віднімаємо 11251024 =101, де 101  десятковийзалишок, який порівнюємо з числом 2⁹= 512. Залишок 101 менше 512, це означає, що на місці 2⁹ ставимо 0. Порівнюємо наступну розрядну вагу 2⁸= 256>101. Знову на місці розрядної ваги 2⁸ ставимо 0. Аналогічно буде і для розряду 2⁷  ставимо 0. Порівнюємо наступну розрядну вагу 2⁶=64<101. У цьому розряді ставимо 1 і віднімаючи 10164=37 отримуємо новий залишок, який порівнюємо з розрядною вагою 2⁵=32<37. В цьому розряді ставимо 1, і віднімаючи 3732=5, отримуємо новий залишок, який легко розписати в чотирьох розрядах, що залишилися: 0101. Таким чином, отримуємо число 10001100101₍₂₎=1125_(10). Перевіримо: 1024+64+32+4+1=1125.

Метод виключає громіздку операцію ділення і при невеликому досвіді легко виконується користувачем. Метод придатний для перекладу як цілої, так і дробової частини числа.