Задачи. А це відношення числа випадків
 Скачать 1.39 Mb.
|
|
Класичне означення ймовірності Припускається, що для даного випробування події рівноможливі, несумісні і єдиноможливі (має місце так звана схема урн). Ймовірність події А – це відношення числа випадків m, що сприяють появі події А, до числа n всіх випробувань в даному експерименті, тобто Р(А)=  ; 0 ≤ P(А) ≤ 1.Приклад 1. Яка ймовірність випадання непарного числа при одноразовому підкиданні грального кубика? Розв’язання: Єдиноможливих, рівноможливих і несумісних наслідків вказаного випробування n=6:1,2,3,4,5,6. Сприятливих наслідків m=3:1,3,5. Тому Р(А)=3/6. Інший варіант розв’язку: числа парні та непарні, тобто n=2; із них сприятливий наслідок один, m=1. Звідки Р(А)=1/2. Приклад 2. Обчислити ймовірності всіх можливих значень суми очок, що випадають при підкиданні 2-ох гральних кубиків. Розв’язання: Очевидно, що найменша сума очок на гранях є 2, а найбільша – 12. Загальне число можливих наслідків буде n=36: кожна цифра 1-го кубика може складатися з 6-ма різними цифрами 2-го кубика (тобто 6х6). Появі суми 2 сприяє один наслідок, суми 3 – два наслідки і т.д. Результати розв’язання задачі наводяться в таблиці. Таблиця
Варто звернути увагу на симетричність розподілу числа m і його зв’язок з сумою очок (зсув діворуч на одиницю). Статистичне визначення ймовірності За ймовірність Р(А) приймається число, навколо якого групуються відносні частоти  для великих n – загального числа випробувань,m – число настання події А в даному експерименті або абсолютна частота. Інколи величину Р*(А) називають частість. Приклад 1. В експериментах Пірсона з підкиданням монети для n=12.000 число випадання герба m=6.019 і Р(А)=0,5016 – частість або відносна частота. Очевидно, Р(А)=0,5. Приклад 2. Відомі дані Чубера про народжуваність хлопчиків в Австрії за період з 1866 р. по 1905 р.: в окремі роки частість 0,515 зустрічалась 11 разів; 0,514 – 17 разів; 0,516 – 9 разів; 0,513 – 2 рази і 0,517 – всього один раз. За всі 40 років спостережень число, навколо якого коливалися значення частостей, є 0,515 (причому відхилення частостей від нього знаходиться в межах 0,1 – 0,2%). Очевидно, Р(А)=0,515, де подія А – народжуваність хлопчика. У таблиці наводяться дані шведської статистики за 1935 рік про народжуваність дівчаток (хлопчиків). Таблиця 1
Очевидно, Р(А)=0,517 – ймовірність народження хлопчика. Незначне відхилення цього результату від 0,515, загальноприйнятого в демографії, пояснюється невеликим n=12. До речі, у давньому Китаї за 2238 років до нашої ери факт народжуваності 514 хлопчиків на 1000 новонароджених був відомий. Вочевидь, результат Р(А)=0,514 (0,515) не залежить від обставин часу, місця та етносу. Приклад 3. У таблиці 2 наведено результати вивчення ситуації, пов’язаної з ризиком повернення кредиту. Таблиця 2
Якщо відповідно позначити події А, В і С, що характеризують ризик повернення типу кредиту, то  ; Р*(В)=0,52 і Р*(С)=0,18.Геометрична ймовірність   Нехай на площині лежить область D площею SD, всередині якої довільно розташована інша менша область d(d D) площею Sd(SdSD). Якщо попадання в меншу область навмання кинутої точки є подія А, то її ймовірність  – це собою відношення площ вищезгадуваних областей.aПриклад 1. Знайти ймовірність того, що навмання взята з круга радіуса R точка належатиме квадрату, вписаному в коло, яке обмежує круг. Якщо подія А бажана, то на підставі означення геометричної ймовірності записуємо 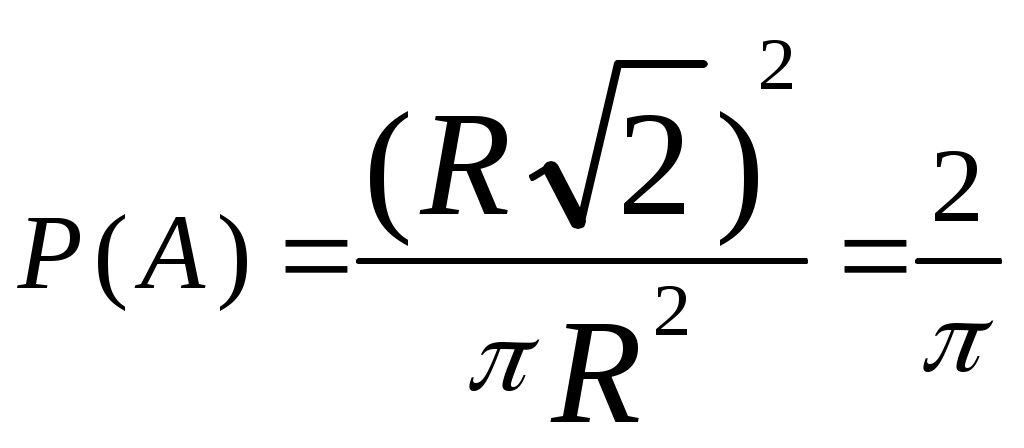 .П 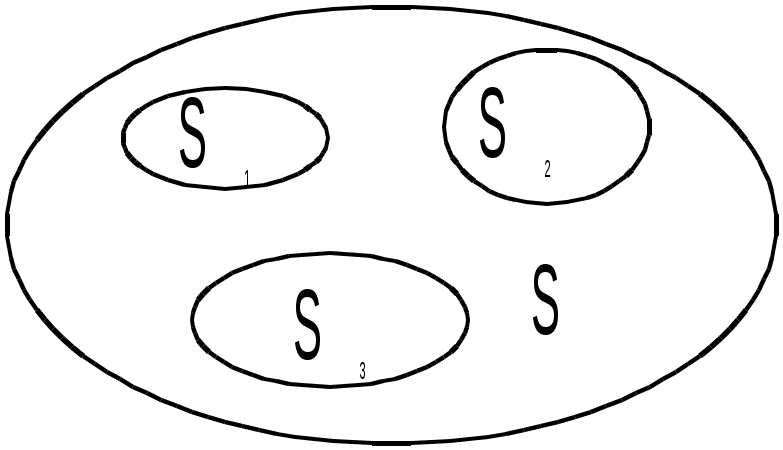 риклад 2. Всередині плоскої фігури площі S лежать три плоских фігури відповідно з площинами S1, S2, S3. Яка ймовірність того, що навмання вибрана з більшої фігури точка не попадає у жодну із фігур S1, S2 та S3?На підставі означення 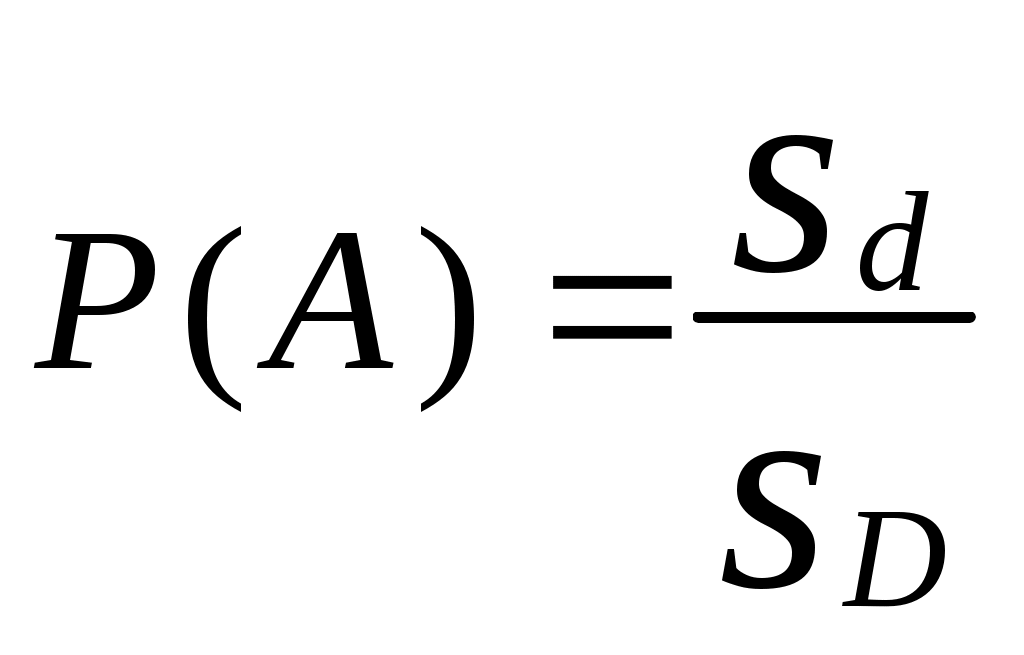 маємо: SD=S; Sd=S-S1-S2-S3 і як наслідок  , де подія А шукана.Приклад 3. На площині розташовано три фігури одна всередині іншої. Площа меншої фігури дорівнює S2, середньої – S1, а більшої – S. Навмання вибрано точку більшої фігури. Яка ймовірність, що точка належатиме меншій фігурі? У силу означення геометричної ймовірності  , де подія А шукана.Приклад 4. Із відрізка [0,2] навмання вибираються два числа x і y. Яка ймовірність, що ці числа задовольняють нерівність x2 ≤ 4y ≤ 4x? Відповідно до умов числа х і узадовольняють систему нерівностей  Тобто точка з координатами (х; у) навмання вибирається з множини точок квадрата, довжина сторони якого рівна 2.Подія, що відповідає умові задачі, полягає у тому, що згадувана точка попадає у заштриховану область – фігуру, координати якої задовольняють нерівністі x2 ≤ 4y ≤ 4x. Площа квадрата – SD= 4. Площа Sdзаштрихованої фігури обчислюється:  . На підставі означення P(A) = 1/3.Приклад 5. Стержень двома випадковими точками ділиться на три частини. Яка ймовірність того, що із отриманих таким чином частин стержня можна утворити трикутник? 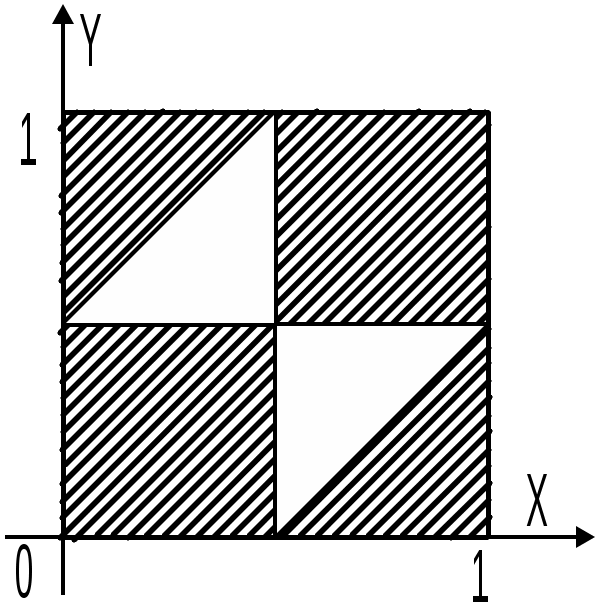 Нехай 1 – довжина стержня, х – відстань від початку стержня до першої точки поділу, у – для другої випадкової точки відстань. В прямокутній системі координат хОу всі рівноможливі значення пари (х,у) відповідають квадрату площею 1. Відшукаємо область несприятливих випадків, тобто таких пар (х,у), коли із відрізків не можна скласти трикутник. Таке відбувається тоді, коли один із відрізків більший або дорівнює сумі двох інших, тобто довжина одного з відрізків ≥ 0,5. Цей факт матиме місце за трьох умов: а) х< 0,5 і y≤ 0,5; або б) x≥ 0,5 і у > 0,5; або в) |x-y| > 0,5. На малюнку вказаним умовам відповідає заштрихована область, незаштрихована – це сприятливі наслідки випробування. Шукана ймовірність – це відношення площ незаштрихованої області Sd і квадрата SD, тобто P(A)=1/4.Зауваження. Для одновимірного простору подій, наприклад випадкова точка падає на відрізок L, всередині якого лежить інший відрізок l, ймовірність події А попадання точки на l – це відношення згадуваних довжин, тобто  . Відповідно для тривимірного простору – відношення певних об’ємів тіл. Елементи комбінаторики Сполученнями називають довільні групи, складені з будь-яких об’єктів (елементів). Існують три види сполучень: розміщення, перестановки або переставлення, комбінації. Розміщеннями із n-елементів по m (m≤n)-взятих називають такі сполуки, які відрізняються між собою або самими об'єктами, або їх порядком розташування. Число розміщень:  або  , де n!=1·2·3…(n-1)·n і читається “ен факторіал”.Приклад 1. Скільки трицифрових чисел з різними цифрами можна скласти з елементів {1,2,3,4,5}, щоб жоден з них не повторювався?  = 5·4·3 = 60.Приклад 2. Скільки трицифрових чисел з різними цифрами можна скласти з елементів {0,1,2,3,4}? Із загальної кількості потрібних чисел треба відкинути ті, що починаються на 0. Їх – =12. Отже, шукана кількість 50 – 12 = 48.Приклад 3. Скількома способами можна присудити першу, другу та третю премії трьом особам з 10?  = 10·9·8 = 720.Перестановками (переставленнями) називаються розміщення із n елементів по n взятих, тобто такі сполучення відрізняються між собою тільки порядком об'єктів. Число перестановок  Приклад 1. Скільки п’ятицифрових чисел можна утворити з множини елементів {0,1,2,3,4}, щоб жодна цифра не повторювалась? Загальна кількість п’ятицифрових чисел – PS = 5! = 1·2·3·4·5 = 120. Вилучаємо ті, що починаються на 0, тобто P4 = 4! =2 4. Отже, 120 – 24 = 96 шуканих п’ятицифорвих чисел. Приклад 2. Скільки різних “слів” можна дістати переставленням букв у слові “математика”?  .У знаменнику 2! відповідає числу повторень букви “м”, 3!- “а”, 2!- “т”. Приклад 3. Скількома способами порівну можна роздати 4-м гравцям 28 костей доміно?  , що приблизно дорівнює числу секунд у 150 млн. років. Комбінаціями із n-елементів по m-взятих називають сполуки, які відрізняються між собою хоча б одним елементом. Число комбінацій  .Важлива для обчислень властивість  .Приклад 1. Для премії 3-м студентам куплено 12 книг. Скількома способами можна розділити ці книжки, щоб кожен учень одержав по 4 книжки. Одному студенту вручити премію існує число можливостей  . Тоді для інших двох щоразу залишатиметься 8 книг, з яких можна скласти ще  наборів (при цьому 2-й і 3-й студенти одержать по 4 книги). Тому всього буде наборів · . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||