Задачи. А це відношення числа випадків

• Название: А це відношення числа випадків
• Анкор: Задачи
• Дата: 26.10.2020
• Размер: 1.39 Mb.
• Имя файла: 91a2f1e933af52685c74dd82a98848c1 (1).doc
• Тип: Документы; #145858
• страница: 3 из 10

Приклад 6. Ймовірність несвоєчасної сплати податків для трьох підприємців відповідно дорівнює 0,1; 0,15; 0,2. Знайти ймовірність несво­єчасної сплати податків хоча б одним із підприємців.

Якщо події A₁, A₂, A₃ – несвоєчасна сплата податків відповідно першим, другим і третім підприємцем, то враховуючи, що A₁, A₂, A₃ – незалежні і сумісні, використаємо теорему 5, попередньо обчисливши:

Р(





Р(А)=1 (А)=1– Р( =1–0,9∙0,85∙0,8 = 0,388.
Теорема 6. Про повну ймовірність

Ймовірність події А, яка може відбутися тільки при умові появи однієї із сумісних подій В_i, де і=1,2…,n, що утворюють повну групу подій, дорівнює сумі добутків ймовірностей кожної із цих подій на відповідну умовну ймовірність події А.

Р(А)= ,

де
Приклад 7. Вивчаються результати заліку з теорії ймовірностей у трьох групах. У першій групі є 30 студентів, з них 8 отримали відмінну оцінку, а в другій відповідно 28 і 6, в третій відповідно 32 і 8. Яка ймо­вірність, що навмання вибраний студент отримав на заліку відмінну оцінку?

Позначимо через А подію, що навмання вибраний з трьох груп студент за результатами заліку з теорії ймовірностей отримав відмінну оцінку. Ця подія може відбутися тоді, коли студента вибрано з першої групи (відбулася подія В₁) або другої (В₂), або третьої (В₃). За статистичним означенням ймовірності .

Використовуємо формулу повної ймовірності:

Р(А)= .

Якщо за умовою задачі:

то

Р(А) = .
Теорема 7. Теорема гіпотез

Ймовірність події за даною гіпотезою дорівнює ймовірності гіпотези до випробування помноженій на ймовірність події за цією гіпотезою, поділе­ній на повну ймовірність, обчислену після випробування:

. (*)

(*) – формула Байєса
Приклад 8. Дві економічні операції, що проводяться підприємцем одночасно для досягнення однієї загальної мети, мають ймовірність успіху, рівну р₁=0,8; p₂=0,6. Необхідно визначити ймовірність того, що досягнуто успіху в результаті першої операції.

Нехай гіпотеза А₁ успіх першої економічної операції, Р(A₁)=0,8; гіпотеза А₂ , успіх другої економічної операції, Р(A₂)=0,6.

Проведені економічні операції можуть дати результати:



Відповідні ймовірності:

;

;

;

.
Мета (подія С) буде досягнена в останніх трьох випадках, тому її ймовірність в першому випадку – 0, а в трьох останніх – 1.

Використовуючи формулу Байєса маємо:



Повторні незалежні випробування
Ймовірність P_n(k) появи події А k раз серед nнезалежних випро­бувань дається формулою Бернуллі:

, (*)

де – число всіх можливих комбінацій зга­дуваного типу, p=p(A) – ймовірність настання незалежної по­дії, q=1–p.

Сукупність P_n(k) утворює біномінальний розподіл, при­чому .

По-іншому: ,

де ліва частина відповідає ймо­вірності настання події хоча б один раз, тобто із формули Бернуллі.

Найвірогідніше число k₀ настання події задовольняє подвійну нерівність npи np– q≤k₀≤np+p, причому k₀=[np+p] є ціла частина числа.

Вже для двоцифрового n застосування формули (*) пов’язане із обчис­лювальними труднощами. Тоді застосовується локальна теорема Лапласа:

, , , .

Результат обчислень тим кращий, чим більше n. Значення функції φ(x) зведені в таблицю, причому для x>3,99 значення φ(x)0.

Для великих n та малих р користуються формулою Пуассона:

, де .

Інтегральна теорема Лапласа P(a≤k≤b)()–() визнає ймовірність події А, що наступає не менше а раз і не біль­ше b раз,

де , – функція Лапласа, непарна , значення якої зведені в таблицю, причому значенням х>4,5 відповідають .

Ймовірність відхилення: частоти від найвірогіднішого числа здій­снюється за формулою 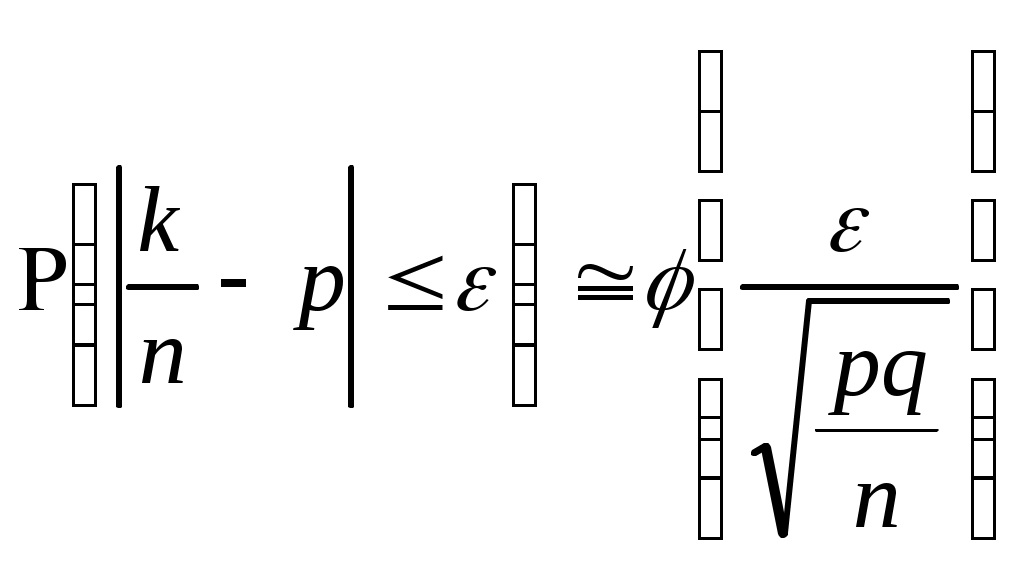; частоти від постійної ймовірності –

Приклад 1. На сотню металевих брусків припадає 30 із зазубринами. Яка ймовірність, що для випадково взятих 7 брусків без дефектів буде не більше двох?

Розв’язання. Якщо подія А відповідає бруску без дефекта, то Р(А)= Тоді n=7, k≤2, тобто шукана ймовірність

,

застосовуючи формулу Бернуллі
Приклад 2. У середньому брак виробництва складає 7,5 %. Виз­начити найвірогідніше число стандартних виробів у партії із 39 штук.

Розв’язання. Якщо q=0,075, то р=0,925 є ймовірність випуску стан­дартної деталі: n=39. На підставі подвійної нерівності маємо

39∙0,925–0,075 ≤ k₀ ≤ 39∙0,925+0,925 маємо 36=k₀ або k₀=37.
Приклад 3. При скількох пострілах найвірогідніше число попадань рівне 16, якщо ймовірність попадання в окремому пострі­лі 0,7?

Розв’язання. Отже, k₀=16; р=0,7 і q=0,3. Складаємо подвійну нерівність 0,7n–0,3 ≤ 16 ≤ 0,7n+0,7. Звідки і . Число всіх пострілів може бути 22 або 23.
Приклад 4. Ймовірність попадання в мішень 0,7. Яка ймовір­ність того, що із 20 пострілів 15 будуть вдалими?

Розв’язання. n=20, k=15, p=0,7, q=0,3. Щоб скористатися формулою локальної теореми Лапласа , послідовно обчислю­ємо:

а) ; б) ;

в) по таблиці ; г) .
Зауваження. На підставі формули Бернуллі маємо

.

Логарифмуючи, дістаємо lgP₂₀(15)=lg3+lg16+lg17+lg19+151lg0,7=1,2524.

Звідки P₂₀(15)=0,179
Приклад 5. При транспортуванні ймовірність пошкодити виріб дорівнює 0,0005. Обчислити ймовірність, що при цьому із усіх виробів числом 4000 тільки від 3 до 5 будуть пошкодженими.

Розв’язання. n=4000, р=0,0005; λ=np≡2. Скористаємося формулою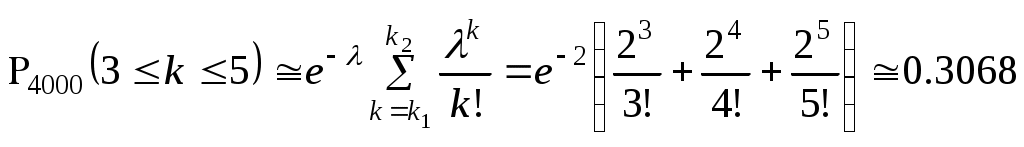

.
Приклад 6. Частка виробів вищого сорту для продукції заводу складає 60 %. Яка ймовірність, що із 1000 шт. число згадуваних виро­бів знаходиться в межах від 580 до 630?

Розв’язання. За умовою задачі маємо: n=1000; р=0,6; q=0,4; а=580; в=630.

; ;

; ;

;

Приклад 7. Ймовірність появи виробу 1-го сорту серед продук­ції – 0,7. Відхилення згадуваних виробів від найвірогіднішого їх числа серед 400 шт. За абсолютною величиною дорівнює 25. Обчис­лити ймовірність такого відхилення.

Розв’язання. За умовою задачі маємо: n=400; ε=25; р=0,7; q=0,3. Тоді =np=280; ; ; ; подвійна нерівність записується 255 ≤ k₀ ≤ 305..
Приклад 8. Ймовірність появи події А в окремому випробу­ванні – р=0,6. Знайти ймовірність того, що для 150 випрбувань частота настання такої подїї буде різниться від її ймовірності не більше, ніж на 0,03.

Розв’язання. n=150, р=0,6, q=0,4, ε=0,03. Треба шукати ймовірність , яка дорівнює .
Види випадкових величин та способи їх задання
Випадкова величина (ВВ) позначається Х; У; Z, у результаті випробування приймає певні випадкові значення х, у, z.

Дискретна випадкова величина (ДВВ) приймає відокремлені, ізольовані значення з відповідними ймовірностями.

Неперервна випадкова величина (НВВ) приймає всі значення з деякого скінченного або нескінченного проміжку.

Закон розподілу ВВ відображає зв’язок між можливими значеннями випадкової величини і відповідними їм імовірностями.

У випадку ДВВ цю залежність задають таблично, аналітично та графічно. У випадку табличного розподілу:

Х	х1	х2	. . .	хк
Р	р1	р2	. . .	рк

Де , і . (1).
Закон розподілу ВВ задається інтегральною або диференціальною функціями розподілу.

Інтегральна функція розподілу – F(x) : F(x)=P(X
Її властивості:

0≤F(x)≤1;

F(x) – неспадна функція; ймовірність того, що випадкова величина Х прийме значення з інтервалу (а;b), обчис­люється за формулою:

P(a<x<b)= F(b)–F(a) . (2)

Диференціальна функція розподілу або щільність розподілу НВВ

f(x)=F(x) (3)

Її властивості:

f(x)≥ 0, оскільки є похідною від неспадної функції F(x);

, оскільки {-∞ < X < +∞} – вірогідна подія;

ймовірність того, що НВВ прийме значення з інтервалу (а;b), обчислюється за формулою:



Графік диференціальної функції f(x)називають кривою розподілу.
Приклад 1. За даними митного поста 20 % осіб не декларують весь товар, який оподатковується. Випадково відібрано 5 осіб. ДВВ Х – це кількість осіб, що не задекларували весь товар. Записати закон розподілу Х у вигляді таблиці.

Розв’язання. Усі можливі значення Х утворюють універсум: Ω={0;1;2;3;4;5}.

Позначимо А={дана особа не задекларувала весь товар}. За умовою р(А)=0,2. Приклад задовольняє умови схеми Бернуллі – випробування незалежні та мають однакову ймовірність. Для n=5 та p=0,2 застосовуємо формулу Бернуллі:

P_n (k) = p^k(1-p)^n-k, k=0,1,...5

P({X=0}) = P₅(0)= (0,2)⁰ (0,8)⁵ ≈0,32768;

P({X=1}) = P₅(1)= (0,2)¹ (0,8)⁴ ≈0,4096;

P({X=2}) = P₅(2)= (0,2)² (0,8)³ ≈0,2048;

P({X=3}) = P₅(3)= (0,2)³ (0,8)² ≈0,0512;

P({X=4}) = P₅(4)= (0,2)⁴ (0,8)¹ ≈0,0064;

P({X=5}) = P₅(5)= (0,2)⁵ (0,8)⁰ ≈0,00032.

Отримані результати внесемо в таблицю:

Х	0	1	2	3	4	5
Р	0,32768	0,4096	0,0512	0,0064	0,0064	0,00032

Графік функції розподілу для ДВВ має вигляд сходинок, висота кожної з яких – р_і. Для даної задачі графік функції розподілу F(x) зоб­ражений на малюнку 1.