Задачи. А це відношення числа випадків
 Скачать 1.39 Mb.
|
|
П  риклад 2. ВВ задана функцією розподілу: 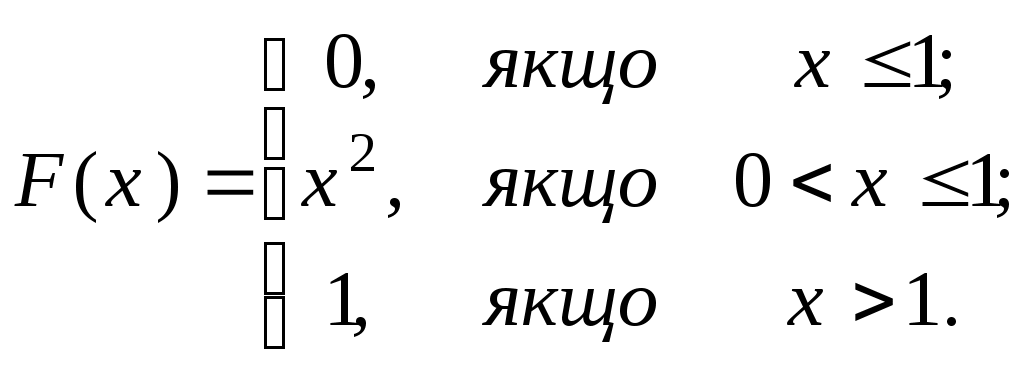 Знайти щільність розподілу; ймовірність того, що у результаті випробування Х прийме значення з інтервалу (–2; 0,5); побудувати графіки функцій F(x) та f(x). Розв’язання. Оскільки f(x)=F’(x), то  Ймовірність того, що в результаті випробування Х прийме значення з інтервалу (–2; 0,5), шукаємо за формулою (2) Р(–2 Графіки функцій F(x) та f(x): Приклад 3. ВВ задана функцією розподілу F(x)=x2–4x+4. Визначити область значень випадкової величини Х та ймовірність того, що Х≥2,3. Розв’язання. Оскільки 0≤F(x)≤1, то має виконуватись подвійна нерівність: 0≤х2–4х+4≤1. Якщо область значень випадкової величини [a;b], то F(a)=0; F(b)=1. Маємо F(a) = a2–4a+4=0 a=2. F(b) = b2–4b+4=1 b1=3; b2= 1. Зрозуміло, що в проміжку [a;b] має виконуватись нерівність a<b, тому область визначення НВВ X буде [2;3]. Обчислимо ймовірність Р(Х≥2,3). Оскільки події {Х≥2,3} та {Х< 2,3} протилежні, то P(Х≥2,3)=1–P(X<2,3)=1–F(2,3) = 1–( 2,32–42,3+4)=1–0,09=0,91. Приклад 4. Щільність ВВ задано: 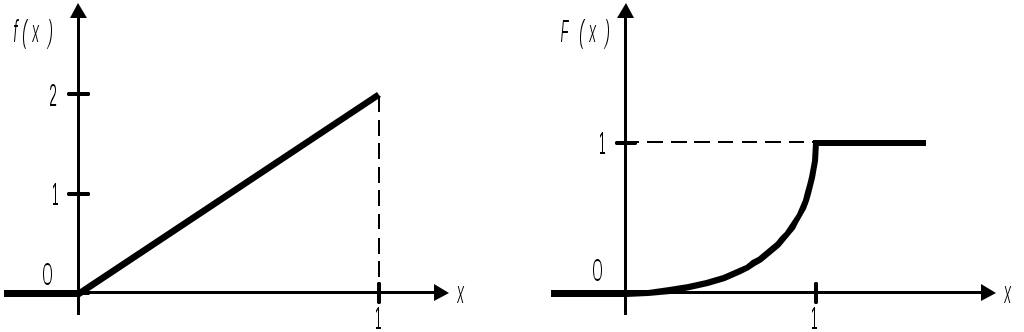  Знайти параметр А та функцію розподілу F(x). Розв’язання. Параметр А знайдемо з 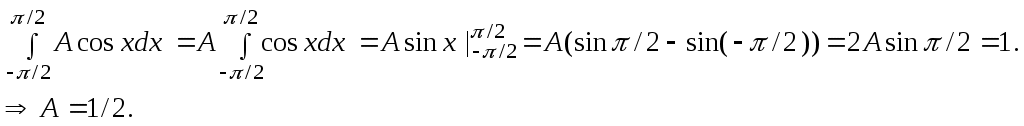 . У даному випадку: Функцію розподілу F(x) знайдемо за формулою  При х<–/2:  При -/2  x /2:  При x >/2:   Тобто маємо таку інтегральну функцію розподілу 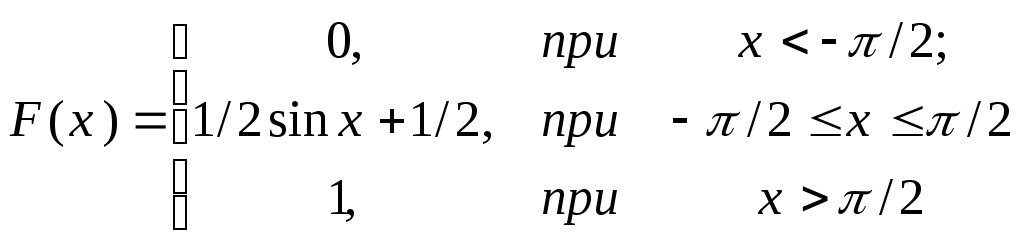 Приклад 5. Задано функцію розподілу F(x) випадкової величини Х, що залежить від параметра а. Знайти значення параметра а; щільність розподілу f(x); ймовірність Р(–2 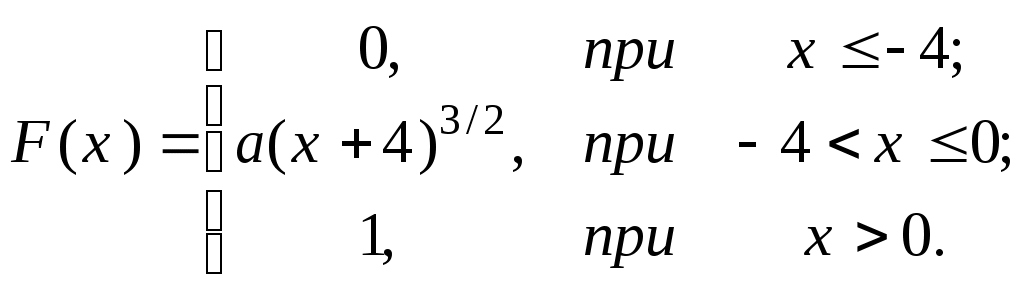 Розв’язання. За формулою (2) маємо F(0)–F(–4) = 1. Скористаємось цією рівністю для знаходження значення параметра а: F(0)=а(0+4)3/2 =а43/2= 8а; F(–4)=а(–4+4)3/2=а0=0; F(0)–F(–4)=8а–0=8а=1, звідси а=1/8. Диференціальна функція розподілу f(x)=F(x). 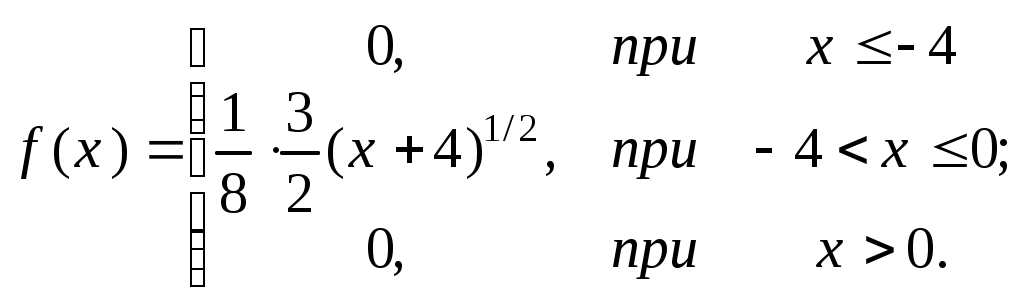 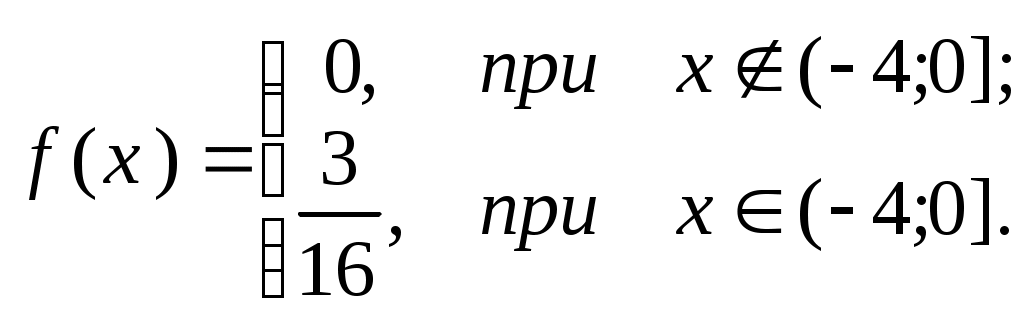 Для обчислення Р(–2 P(a Тут F(–2  (–2+4)3/2=1– 23/2 = 1– . Числові характеристики дискретних випадкових величин (ДВВ) Математичне сподівання ДВВ Х – це число, що дорівнює сумі добутків усіх можливих значень Х на відподвідні їм ймовірності. Позначають математичне сподівання М(Х) або mX і обчислюють за формулою  (1)Зауваження. Математичне сподівання (МС) – це величина, навколо якої групуються можливі значення ВВ. Основні властивості М (Х) М(С)=С, де С=const. М(СХ)=С М(Х), де С=const. Якщо Х1, Х2,...Хn – взаємонезалежні ДВВ, тоді М(Х1 Х2 ...Хn)=М(Х1) М(Х2) ...М(Хn). М (Х1+ Х2+...+Хn)=М (Х1)+М(Х2)+...М(Хn). Дисперсія ДВВ Х – це міра розсіювання можливих значень Х відносно центру розподілу, і вона дорівнює математичному сподіванню квадрата відхилення ДВВ Х від її математичного сподівання. Позначають дисперсію D(X) або DX. Математично означення дисперсії записується наступним чином D(X) = M((X- M(X))2) (2) Основні властивості D(X): D(X)≥0, для будь-якої ДВВ X. D(C)=0, де C=const. D(CX)=C2 D(X), де C= const. D(X)=M(X 2)–(M(X)) 2 (3) або  (4)Зауважимо, що формулу (4) зручно використовувати для обчислення D(X): D(X1X2...Xn)=D(X1)+D(X2)+...+D(Xn). Середнє квадратичне відхилення ДВВ Х визначається за формулою  (5)Особливо важливими є ДВВ, що приймають значення з множини цілих невід’ємних чисел 0, 1, 2, ... . Ці величини описують реальні задачі. До найбільш поширених законів розподілу ДВВ належать: біномний; Пуассона; геометричний . Біномний закон розподілу ДВВ задається таблицею, в якій ймовірності pk розраховуються за формулою Бернуллі:
Постійні параметри n та p називають параметрами розподілу. Числові характеристики ДВВ Х при біномному розподілі: М(Х)=np (6) D(X)=npq (7)  (8)Якщо в схемі повторних незалежних випробувань n, а число р близьке до 0, і крім того np при n, тоді ДВВ Х, що визначає кількість появ певної події в схемі Бернуллі, має розподіл Пуассона, який задається натупною таблицею.
Числові характеристики ДВВ Х, що має розподіл Пуассона: М(Х)= (9) D(X)= (10) Геометричний розподіл задається формулою Р(Х=m)=pqm-1, (11) де р = Р(А) – ймовірність появи події А в кожному з незалежних випробувань; q= 1–p; ДВВ Х – це кількість випробувань у схемі Бернуллі до першої появи події А. Числові характеристики ДВВ Х, що має геометричний закон розподілу:  (12) (13)Приклад 1. Певний пристрій складається з 4-х комплектуючих. Пристрій протестовано на надійність його компонентів. У таблиці записано розподіл ДВВ Х – кількості компонентів, що припинили свою роботу за 200 перших годин роботи. Знайти М(Х), D(X), (X).
Розв’язання. Математичне сподівання обчислюємо за формулою (1), в даному випадку:  .Дисперсію D(X) обчислюємо за формулою (4): D(X) = M(X2)–(M(X))2  Обчислимо  М(Х2)=00,08+10,2+40,4+90,25+160,07=4,27.Маємо дисперсію D(X)=4, 27–(2,03)2=0,1491. Відповідно середнє квадратичне відхилення (X)=  = 0,386.Приклад 2. Випадкові величини Х та У незалежні і розподілені таким чином
Знайти М(Z), якщо Z= 2XY+X2+3Y–71. Розв’язання. Скориставшись властивостями математичного сподівання, маємо: M(Z)=M(2XY+X2+3Y–71)=M(2XY)+M(X2)+M(3Y)+M(–71) = =2M(XY)+M(X2)+3M(Y)–71=2M(X)M(Y)+M(X2)+3 M(Y)–71. Для розрахунку M(Z)необхідно знайти М(Х), М(Y), М(Х2). Згідно з формулою (1): М(Х)=20,1+70,4+90,5=7,5; М(Х2)=40,1+490,4+810,5=60,5; М(Y)=40,1+60,3=4,6. Маємо M(Z)=27,54,6+60,5+34,6–71=72,3. Приклад 3. Випадкові величини Х та Y незалежні і відомо, що D(X)=2; D(Y)=3. Знайти D(Z)та (Z),якщо Z=3X–Y. Розв’язання. Скористаємось властивостями дисперсії D(Z)=D(3X–Y)=D(3X)+D(Y)=32D(X)+D(Y)=9D(X)+D(Y)=92+3=21. (Z) =  .Приклад 4. Знайти М(Х), D(X), (X), якщо ДВВ Х – кількість виграшних лотерейних квитків, якщо куплено 40 квитків і ймовірність виграшу будь-якого з них – 0,02. Розв’язання. ДВВ Х має біномний розподіл з параметрами n=40; p=0,02. Згідно формул (6) – (8) маємо M(X)=np=400,02=0,8; D(X)=npq=400,020,98 = 0,784; (X)=  = Приклад 5. Ймовірність браку в партії виробів 0,02. Перевіряють партію з 400 виробів, ДВВ Х – кількість бракованих виробів в партіі. Знайти М(Х), D(X), (X). Розв’язання. ДВВ Х має розподіл Пуассона з параметром: =np=0,02400=8. Згідно з формулами (9) – (10 ) маємо: М(Х)= = 8; D(X)==8; (X)=  .Приклад 6. Середнє квадратичне відхилення кожної з 9-ти однаково розподілених ВВ дорівнює 8. Знайти дисперсію середнього арифметичного цих величин. Розв’язання. Згідно з умовою  , томуD(X1)=D(X2)= ... = D(X9)=64. Обчислимо  = D(X1+X2+...+X9)= (D(X1)+ +D(X2) +...+D(X9)) = 964= .Відповідно  |
pqn-1
p2qn-2
pn-1q
