Задачи. А це відношення числа випадків
 Скачать 1.39 Mb. Скачать 1.39 Mb.
|
|
Задача 5. ПОВТОРЕННЯ НЕЗАЛЕЖНИХ ВИПРОБУВАНЬ. ФОРМУЛА БЕРНУЛЛІ, ФОРМУЛИ МУАВРА-ЛАПЛАСА, ФОРМУЛА ПУАССОНА 5.1. Велика партія виробів містить 30% нестандартних. Знайдіть імовірність того, що з п’яти виробів, які випадково відібрали з партії: а) лише один нестандартний; б) принаймні один нестандартний. 5.2. Імовірність того, що пасажир, який звернувся до авіакаси, замовить білет до аеропорту N, становить 0,1. Знайдіть імовірність того, що зі ста пасажирів, якізвернулися до каси, білет до аеропорту N замовлять: а) менше 15 чоловік; б) від 5 до 12 чоловік; в) більше 20 чоловік. 5.3. Радіоапаратура складається з 1000 мікроелементів. Імовірність відмови кожного елемента протягом доби дорівнює 0,002 і не залежить від стану інших елементів. Знайдіть імовірність відмови протягом доби: а) лише двох елементів; б) не більше двох елементів. 5.4. Авіакомпанія виконує протягом місяця 400 рейсів. Імовірність повного комерційного навантаження кожного рейсу становить 0,8. Знайдіть імовірність того, що протягом місяця з повним комерційним навантаженням буде виконано: а) не менше трьохсот рейсів; б) від 250 до 350 рейсів. 5.5. Якість виробу оцінюють незалежно один від одного 4 контролери. Імовірність прийому виробу кожним контролером дорівнює 0,9. Знайдіть імовірність того, що виріб буде прийнятий: а) всіма контролерами; б) принаймні двома контролерами. 5.6. За статистичними даними в середньому 1% клієнтів банку відмовляються від кредиту. Знайдіть імовірність того, що з 300 клієнтів відмовляються від кре- диту: а) не менше трьох клієнтів; б) не більше п’яти. 5.7. На біржі виставлено 10 цінних паперів. Імовірність того, що вони подорожчають протягом одного дня, дорівнює 0,6. Знайдіть ймовірності того, що протягом дня подорожчає: а) рівно 5 паперів; б) не більше ніж 4 папери; в) від 3 до 5 цінних паперів. 5.8. Велика партія ламп містить 1% браку. Знайдіть імовірність того, що серед відібраних навмання восьми ламп виявиться: а) принаймні одна бракована; б) рівно 2 браковані лампи. 5.9. За статистичними даними в середньому 5% рейсів, які виконує авіакомпанія, затримуються за технічними причинами. Знайдіть імовірності того, що з чотирьохсот рейсів, запланованих на наступний місяць, за технічними причинами буде затримано: а) не більше 10% рейсів; б) не менше 3% рейсів. 5.10. Імовірність прольоту пункту обов’язкового повідомлення у призначений час для кожного з чотирьох літаків дорівнює 0,8. Знайдіть імовірність того, що пункт обов’язкового повідомлення у призначений час пролетить: а) принаймні один літак; б) лише два літака; в) не менше трьох літаків. 5.11. Телефонна станція обслуговує 2000 абонентів. Імовірність того, що будь-який абонент зателефонує на станцію протягом години, дорівнює 0,001. Знайдіть імовірність того, що протягом години на станцію зателефонують: а) лише 5 абонентів; б) не більше двох абонентів. 5.12. Інвестор укладає договір на фондовій біржі. Імовірність укладання однієї угоди за день дорівнює 0,7. Виходячи з припущення, що за 10 робочих днів укладається не більше однієї угоди в день, знайдіть ймовірності подій: а) буде укладено рівно 7 угод; б) буде укладено не більше 8 угод; в) жодної угоди не буде укладено. 5.13. Фабрика виробляє 75% продукції вищої якості. Знайдіть імовірність того, що з 300 виробів цієї фабрики кількість високоякісних виробів буде: а) не менше 250; б) від 220 до 235; в) не більше 200. 5.14. Кількість помилок у рахунках торгових підприємств складає 5 %. Аудитор перевіряє 10 навмання вибраних рахунків. Знайдіть імовірність того, що аудитором: а) не буде знайдено жодної помилки; б) буде знайдено лише три помилки; в) буде знайдено від 3 до 5 помилок. 5.15. Імовірність закриття аеропорту за метеоумовами для кожної доби в осінньо-зимовий період дорівнює 0,15. Знайдіть імовірність того, що в цей період аеропорт буде закритий: а) лише 30 діб; б) не більше 30 діб; в) не менше 50 діб. 5.16. Імовірність того, що відвідувач магазину зробить покупку, дорівнює 0,2. Знайдіть імовірність того, що з 10 відвідувачів, які завітали до магазину: а) покупку зроблять рівно 6 відвідувачів; б) покупку не зробить жоден відвідувач; в) покупку зроблять не більше трьох відвідувачів. 5.17. Прилад складається з чотирьох незалежно працюючих вузлів. Імовірність безвідмовної роботи за час t кожного вузла дорівнює 0,7. Знайдіть імовірність того, що протягом часу t будуть безвідмовно працювати: а) всі вузли; б) принаймні один вузол; в) не менше трьох вузлів. 5.18. При транспортуванні пошкоджується в середньому 0,05% скляних виробів. Знайдіть імовірність того, що при транспортуванні 1000 виробів буде пошкоджено: а) рівно 3 вироби; б) не більше двох виробів; в) принаймні один виріб. 5.19. З комплекту, який складається з дев’яти якісних і одного бракованого виробу, навмання по одному відбираються вироби, кожен з яких після визначення якості повертається до комплекту. Знайдіть імовірність того, що у процесі десяти таких відборів бракований виріб буде виявлений: а) принаймні один раз; б) рівно один раз. 5.20. Близько 40 % клієнтів банку використовують спеціальні кредитні картки. Знайдіть імовірність того, що з 25 клієнтів банку, картки використовують: а) рівно 12 клієнтів; б) не менше 10 клієнтів; в) від 15 до 20 клієнтів. 5.21. Фабрика виробляє в середньому 20 % нестандартних виробів. Знайдіть імовірність того, що в партії з 100 штук кількість нестандартних виробів виявиться: а) більшою 2; б) більшою за 5 і меншою за 20. 5.22. Радіостанція аеропорту надсилає 6 повідомлень для екіпажу літака. Імовірність прийому кожного із повідомлень дорівнює 0,6. а). Знайдіть найбільш імовірну кількість повідомлень, прийнятих екіпажем, і відповідну їй імовірність. б). Яка ймовірність того, що екіпаж прийме не менше чотирьох повідомлень? 5.23. На біржі виставлено 100 цінних паперів. Імовірність того, що вони подорожчають протягом одного дня, дорівнює 0,06. Знайдіть ймовірності того, що середцих 100 цінних паперів подорожчає: а) рівно 50 паперів; б) не більше ніж 40 паперів; в) від 30 до 60 цінних паперів. 5.24. Імовірність того, що відвідувач супермаркету зробить покупку, дорівнює 0,7. Знайдіть імовірність того, що з 100 відвідувачів зроблять покупку: а) лише 60 осіб; б) не більше 70 осіб; в) не менше 50 осіб. 5.25. Завод відправив на базу 500 доброякісних виробів. Імовірність пошкодження при транспортуванні кожного виробу дорівнює 0,001. Знайдіть ймовірності пошкодження при транспортуванні: а) рівно двох виробів; б) менше двох виробів; в) принаймні одного виробу. 5.26. Імовірність того, що лампа залишається придатною після t годин роботи, дорівнює 0,1. а) Знайдіть найбільш імовірне число ламп із п'яти придбаних, які залишаться придатними після t годин роботи. б) Яку кількість ламп треба придбати, щоб з імовірністю, не меншою 0,95, принаймні одна з них залишилась придатною? 5.27. Близько 30% клієнтів банку використовують спеціальні кредитні картки. Знайдіть імовірність того, що з 100 клієнтів банку, картки використовують: а) рівно 60 клієнтів; б) не менше 50 клієнтів; в) від 40 до 60 клієнтів. 5.28. Імовірність несвоєчасного відправлення рейсу з аеропорту дорівнює 0,004. Знайдіть імовірність того, що з 500 рейсів несвоєчасно буде відправлено: а) лише 4 рейси; б) не менше чотирьох рейсів; в) принаймні один рейс. 5.29. За даними метеослужби аеропорту кількість нельотних днів в I-му кварталі складає в середньому 10%. Знайдіть імовірність того, що в I-му кварталі буде нельотних: а) лише 10 днів; б) від 5 до 15 днів;в) не більше 10 днів. 5.30. На контроль надійшла партія виробів. Відомо, що 5% всіх виробів не відповідає стандарту. а). Знайдіть найбільш імовірне число нестандартних виробів серед шести перевірених і відповідну йому ймовірність. б). Скільки потрібно перевірити виробів, щоб з імовірністю, не меншою 0,95%,виявити принаймні один нестандартний виріб? II ВИПАДКОВІ ВЕЛИЧИНИ Задача 1. Для даної випадкової величини Х 1) складіть ряд розподілу і побудуйте многокутник розподілу; 2) знайдіть моду, математичне сподівання і дисперсію; 3) знайдіть ймовірність того, що значення випадкової величини більше нуля і не більше М(Х) + 2 s (X). 1.1. Комплект складається з п‘яти деталей 1-го ґатунку, двох деталей 2-го ґатунку і трьох бракованих деталей. Навмання з комплекту відбирається одночасно 3 деталі. Випадкова величина X – кількість бракованих деталей серед відібраних. 1.2. Система складається з трьох пристроїв, які за час t незалежно один від одного можуть вийти з ладу з ймовірностями відповідно 0,1, 0,05 і 0,2. Випадкова величина X – число пристроїв, які вийшли з ладу за час t .. 1.3. Імовірність появи бракованого виробу при оцінці якості партії виробів дорівнює 0,1. Контролер навмання по одному відбирає з партії 4 вироби, але припиняє відбір після появи бракованого виробу і не приймає партію. Випадкова величина Х – кількість відібраних небракованих виробів. 1.4. Імовірність затримки рейсу за метеоумовами аеропорту дорівнює 0,2. Випадкова величина Х – кількість затриманих рейсів з чотирьох, які виконуються з аеропорту. 1.5. Радіостанція надсилає 3 повідомлення для екіпажа, який виконує рейс. Імовірності прийому першого, другого, третього повідомлень відповідно дорівнюють 0,9, 0,8, і 0,7. Випадкова величина Х – кількість прийнятих повідомлень . 1.6. Партія виробів містить 20% нестандартних. Навмання з партії одночасно відбирається 3 вироби. Випадкова величина Х – кількість бракованих виробів серед відібраних. 1.7. Імовірність правильної відповіді студентом на кожне питання викладача дорівнює 0,8. Викладач задає питання до одержання першої неправильної відповіді, але не більше трьох питань. Випадкова величина X – кількість одержаних правильних відповідей. 1.8. Комплект складається з чотирьох виробів вартістю по 4 гривні кожен і шести виробів – по 3 гривні. Навмання з комплекту одночасно відбирається 3 вироби. Випадкова величина Х – сумарна вартість відібраних виробів. 1.9. Авіакомпанія 30% всіх рейсів виконує власним літаковим парком. Навмання вибирається чотири рейси. Випадкова величина Х – кількість рейсів на власному літаковому парку серед вибраних. 1.10. Якість виробу перевіряється трьома контролерами. Ймовірності того, що виріб буде прийнятий першим, другим, третім контролером, відповідно дорівнюють 0,95, 0,9 і 0,8. Випадкова величина Х – число контролерів, які прийняли виріб. 1.11. В партії з 20 виробів 90% мають вищу якість. Навмання з партії одночасно відібрано 3 вироби. Випадкова величина Х – число виробів вищої якості серед відібраних. 1.12. При обставинах, що склалися, ймовірність точного вимірювання штурманом кута знесення дорівнює 0,8. Штурман 4 рази виміряв кут. Випадкова величина Х – число точних вимірювань кута. 1.13. Авіафірма протягом дня виконує 3 рейси. Імовірності затримки першого, другого, третього рейсів за метеоумовами дорівнює відповідно 0,1; 0,3 і 0,5. Випадкова величина Х – число затриманих за метеоумовами рейсів. 1.14. Брак в продукції цеху складає 5%. З денного виробітку контролер навмання відбирає по одному виробу до виявлення першого бракованого, але не більше 4-х виробів. Випадкова величина Х – число відібраних придатних виробів. 1.15. За даними метеослужби аеропорту в лютому кількість нельотних днів складає в середньому 20%. Випадкова величина Х – число нельотних днів серед 4-х наступних. 1.16. З комплекту, який складається з шести виробів 1-го гатунку, п’яти – 2-го гатунку і чотирьох бракованих виробів, навмання відібрані 3 вироби. Випадкова величина Х – число небракованих виробів серед відібраних. 1.17. Ймовірність того, що стрілець влучить у мішень при одному пострілі, дорівнює 0,9. Стрільцеві видають патрони доти, доки він не зробить промах але не більше 6. Випадкова величина Х - кількість патронів, що були видані стрільцеві. 1.18. В контейнері знаходяться 5 виробів, один з яких бракований. Навмання по одному з контейнера відбираються вироби до появи бракованого. Випадкова величина Х – число відібраних виробів. 1.19. При підльоті до аеродрому літак має запас пального для трьох заходів на посадку. Імовірність благополучної посадки при першому заході дорівнює 0,8, при другому – 0,9, при третьому – 0,95. Випадкова величина Х – число заходів літака на посадку. 1.20. Оператор обслуговує 3 незалежно працюючі верстати. Імовірність того, що впродовж години верстату не знадобиться втручання оператора, дорівнює: для першого верстата – 0,75, для другого – 0,8, для третього – 0,9. Випадкова величина Х – число верстатів, яким не знадобиться втручання оператора. 1.21. На шляху руху автомобіля 5 світлофорів, кожен з яких дозволяє або забороняє рух з імовірністю 0,5. Випадкова величина Х – число світлофорів, пройдених автомобілем до першої зупинки. 1.22. Імовірність виготовлення підприємством нестандартного виробу дорівнює 0,1. Із партії виробів контролер навмання по одному відбирає до п’яти виробів, припиняючи відбір після одержання першого нестандартного виробу. Випад- кова величина Х - число відібраних стандартних виробів. 1.23. Оператор обслуговує 4 незалежно працюючі верстати. Імовірність того, що впродовж години кожному з верстатів знадобиться втручання оператора, стала і дорівнює 0,2. Випадкова величина Х – число верстатів, яким впродовж години не знадобилось втручання оператора. 1.24. Комплект містить 6 виробів вартістю 3 гривни кожен і 4 вироби – по 2 гривні. Навмання з комплекту відбирається 3 вироби. Випадкова величина Х – сумарна вартість відібраних виробів. 1.25. Прилад складається з чотирьох незалежно працюючих вузлів. Імовірність того, що кожен з вузлів не вийде з ладу за час t, стала і дорівнює 0,75. Випадкова величина Х – кількість вузлів, які не вийшли з ладу за час t. 1.26. В екзаменаційному білеті 4 питання, на кожне з яких студент може відповісти з імовірністю 0,7. Випадкова величина Х – кількість питань екзаменаційного білету, на які студент може відповісти. Знайдіть імовірність того, що студент складе іспит, якщо для цього необхідно відповісти принаймні на 3 питання. 1.27. Комплект складається з шести посудин місткістю 2 літри кожна і чотирьох посудин – по 1 літру кожна. Випадкова величина Х – сумарна місткість трьох навмання відібраних з комплекту посудин. 1.28. Диспетчер керує підходом трьох літаків, які заходять на посадку з трьох коридорів. Імовірність посадки літака без відходу на другий круг з першого коридору дорівнює 0,95, з другого – 0,92 і з третього – 0,9. Випадкова величина Х –кількість літаків, які виконали посадку без відходу на другий круг. 1.29. На маршруті виконання рейсу є 5 районів, у кожному з яких з імовірністю 0,6 можлива поява грозового фронту. Випадкова величина Х – кількість районів, які пройшов літак до зустрічі з грозовим фронтом. 1.30. Імовірність прольоту кожним із чотирьох літаків в призначений час пункту обов’язкового повідомлення дорівнює 0,9. Випадкова величина Х – кількість літаків, які пролетіли пункт обов’язкового повідомлення в призначений час. Види випадкових величин та способи їх задання Задача 2. 2.1. Визначити, які з випадкових величин є дискретними, а які неперервними: а) зріст студентів вашої групи; б) кількість телефонних дзвінків до певного абонента; в) вага новонародженої дитини; г) кількість сигарет, спалених за день; д) кількість бракованих виробів у партії; е) кількість води, яку використовує місто за добу ; є) атмосферний тиск ; ж) тривалість роботи телевізора до першої поломки. 2.2. Двічі підкидають гральний кубик. Описати простір елементарних подій . Нехай Х – ДВВ, що дорівнює сумі очок, які випали. Побудувати розподіл Х у вигляді таблиці та графік F(x). 2.3. Серед 8 деталей є 2 нестандартні. Навмання беруть 2 деталі. Знайти закон розподілу числа стандартних деталей серед відібраних. 2.4. З 25 контрольних робіт, серед яких 5 оцінені на “відмінно”, навмання беруть 3 роботи. Знайти закон розподілу ДВВ Х – кількості робіт, серед відібраних, що оцінені на “відмінно”. Знайти ймовірність того, що Х>0. 2.5. Два лучника роблять по 2 постріли по одній мішені. Ймовірність влучення в мішень для першого стрілка 0,5, для другого – 0,6. Знайти закон розподілу ДВВ Х, що дорівнює загальному числу влучень у мішень. 2.6. На шляху руху автомобіля 6 світлофорів, кожен з яких з ймовірністю 0,5 дозволяє або забороняє рух автомобіля. Скласти ряд розподілу та побудувати функцію розподілу кількості світлофорів, які автомобіль пройшов без зупинки. 2.7. Зроблено 3 постріли з ймовірностями влучення в мішень відповідно рівними 0,6; 0,4; 0,5. Знайти закон розподілу ВВ Х – кількості числа влучень. Побудувати графік функції розподілу. 2.8. Знайти закон розподілу Х – кількості виграшних лотерейних квитків, якщо всього придбано 10 квитків, а ймовірність виграшу для кожного з них – 0,2. Побудувати графік F(x). 2.9. При перевезенні якісних виробів ймовірність пошкодження кожного виробу дорівнює р. Знайти закон розподілу ДВВ х, що дорівнює кількості пошкоджених виробів, якщо перевозилось n виробів.
2.10. Робітник обслуговує 4 незалежно працюючі верстати. Ймовірність того, що протягом однієї години верстат не буде потребувати уваги робітника, для першого верстата – 0,6; для другого – 0,7; для третього – 0,75; для четвертого – 0,8. Знайти закон розподілу випадкової величини Х, що дорівнює числу верстатів, які будуть потребувати уваги робітника. 2.11. Статистика свідчить, що 7 % працездатних людей – безробітні. Навмання вибрано 4 особи. Побудувати закон розподілу випадкової величини Х, що визначає кількість безробітних серед цих 4-ох осіб. 2.12. Прилад складається з 5-ти елементів, ймовірність несправності кожного з них дорівнює 1/9. Скласти закон розподілу випадкової величини Х – числа несправних елементів. 2.13. Задано функцію розподілу ймовірностей F(x) випадкової величини Х, що залежить від параметра а. Визначити значення параметру, знайти f(x) та Р(<x<), якщо: 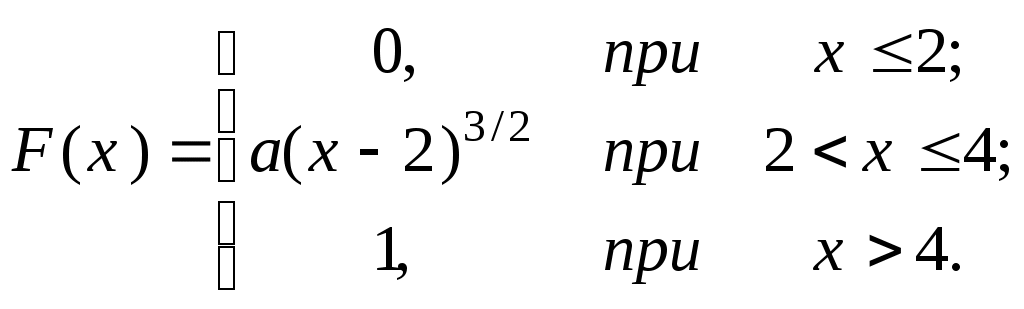 =1; =3. 2.14 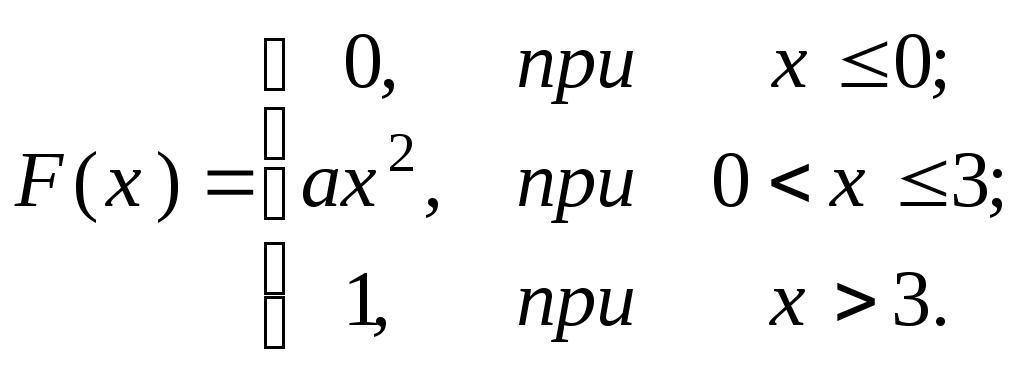 =–1; =1. 2.15 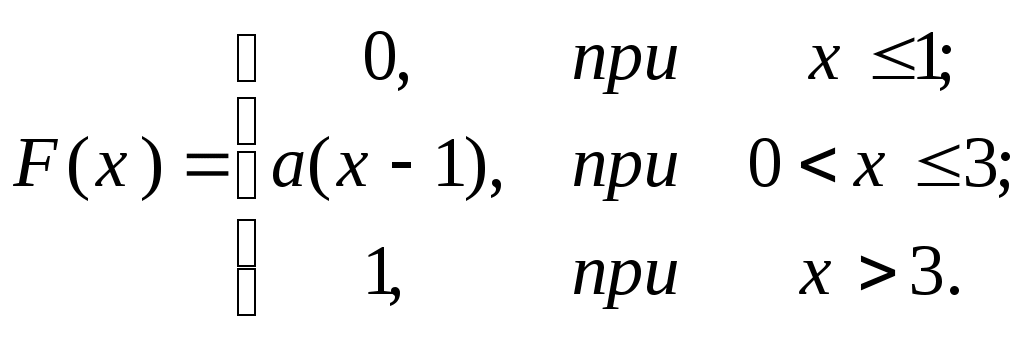 =0; =2. 2.16 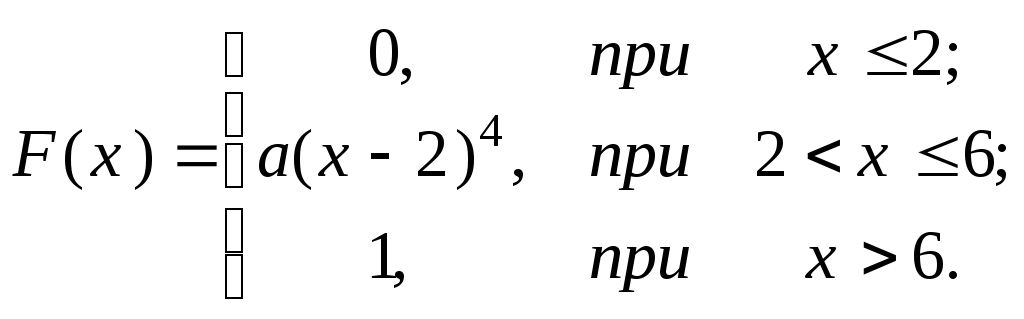 =1; =4 2.17 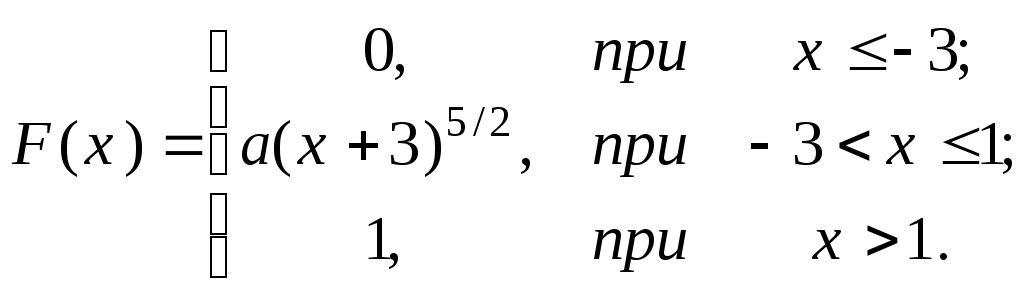 =–2; =0. 2.18 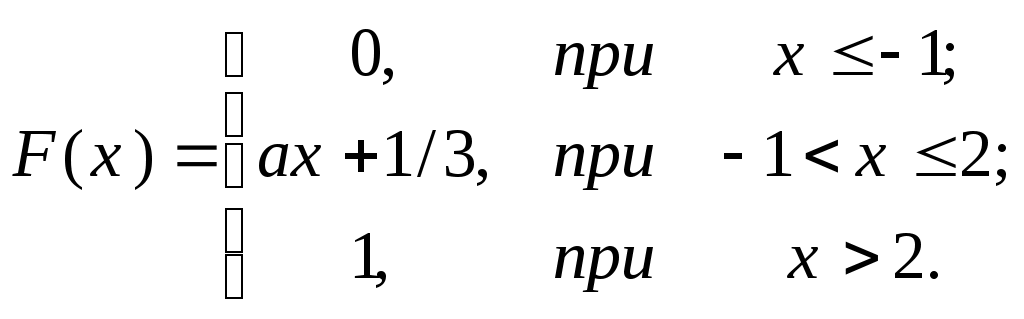 = 0; =1/2. 2.19 Випадкова величина Х задана функцією розподілу F(x). Визначити область значень випадкової величини Х та ймовірність того, що x ≥ при умовах: а) F(x)=x2–6x+9, = 3,5; б) F(x)=x2+10x+25, = –4,5; в) F(x)=x2–8x+16, = 4,6; г) F(x)=x2–12x+36, = 6,3; д) F(x)=x2+4x+4, = –1,7; е) F(x)=x2+8x+16, = –3,6. |
