Задачи. А це відношення числа випадків

• Название: А це відношення числа випадків
• Анкор: Задачи
• Дата: 26.10.2020
• Размер: 1.39 Mb.
• Имя файла: 91a2f1e933af52685c74dd82a98848c1 (1).doc
• Тип: Документы; #145858
• страница: 7 из 10

Приклад 1. Статистичні дослідження рівня доходу одного працю­ю­чого за день дали такі результати:

хі (дохід у грн.)	6	7	8	9	10	11	12	13	14
ni (число людей)	1	2	3	20	25	24	15	7	3

З надійністю =0,95 при значенні =3 побудувати інтервал довір’я для математичного сподівання.

Розв’язання. За припущенням, що рівень доходу підпоряд­ко­ву­ють­ся нормальному закону, скористаємося формулою ( ).

За таблицею для інтегральної функції Лапласа Ф(t) знаходимо:

2Ф(t)=0,95; t=1,96.

За даними вибірки обчислимо:

=(6+14+24+180+250+264+180+51+42) =9,11.

Тоді довірчий інтервал доходу є:

(9,11- ;9,11+ ); (8,522;9,698).

Приклад 2. Вибіркове дослідження прибутків підприємців за місяць дало результати:

Прибуток (тис.гр.)(хі)	1	3	4	5	6	7
Частота (ni)	1	1	2	3	2	1

Побудувати довірчий інтервал для математичного сподівання, а припускаючи, що генеральна сукупність Х розподілена нормально з надій­ністю =0,95, розрахувати інтервал для .

Розв’язання. Знаходимо числові характеристики вибірки:

=(1+3+8+15+12+7) =4,8;

Д_В=(1+9+32+75+72+49) -4,8²=23,8-23,04=0,76.

Виправлене середнє квадратичне відхилення:

.

За надійністю =0,95 і числом ступенів вільності k=10-1=9 за табли­цею знаходимо =2,31. Отримані числові дані підставляємо у формулу:

( ).

Тоді межі інтервального довір’я наступні:

=4,8-0,71=4,09;

.

Отже, інтервал довір’я для місячних прибутків підприємців у тис. грн. з надійністю – 0,95 є (4,09; 5,51).

Для розрахунку інтервалу довір’я величини  знайдемо за табли­цями значень q(,n) при =0,95 і n=10-q=0,65. Тоді кінці інтервалу мають такі значення:

S(1-q)=0,977(1-0,65)=0,342;

S(1+q)=0,977(1+0,65)=1,612.

Отже, інтервал довір’я 0,341<1,612.

Обробка вибірки методом найменших квадратів (МНК)
Для обчислення параметрів а та b лінійної функціональної залежності y=ax+b між випадковими величинами X та Y користуються формулами: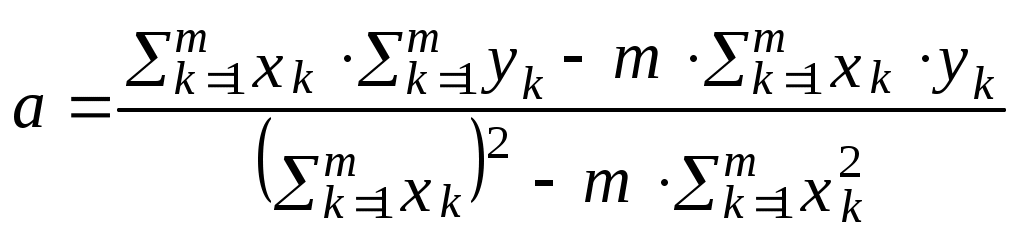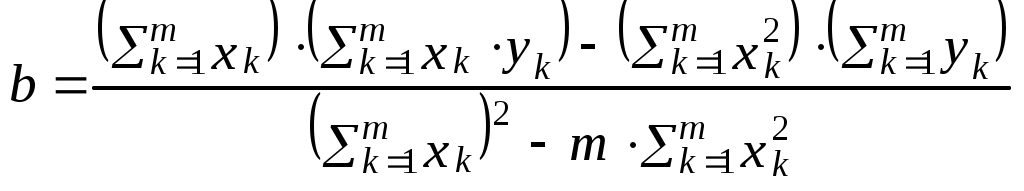

;
.

Якщо кількість х_k та y_k велика, то початок розрахунків величин х_k переносять в середнє значення усіх х_k.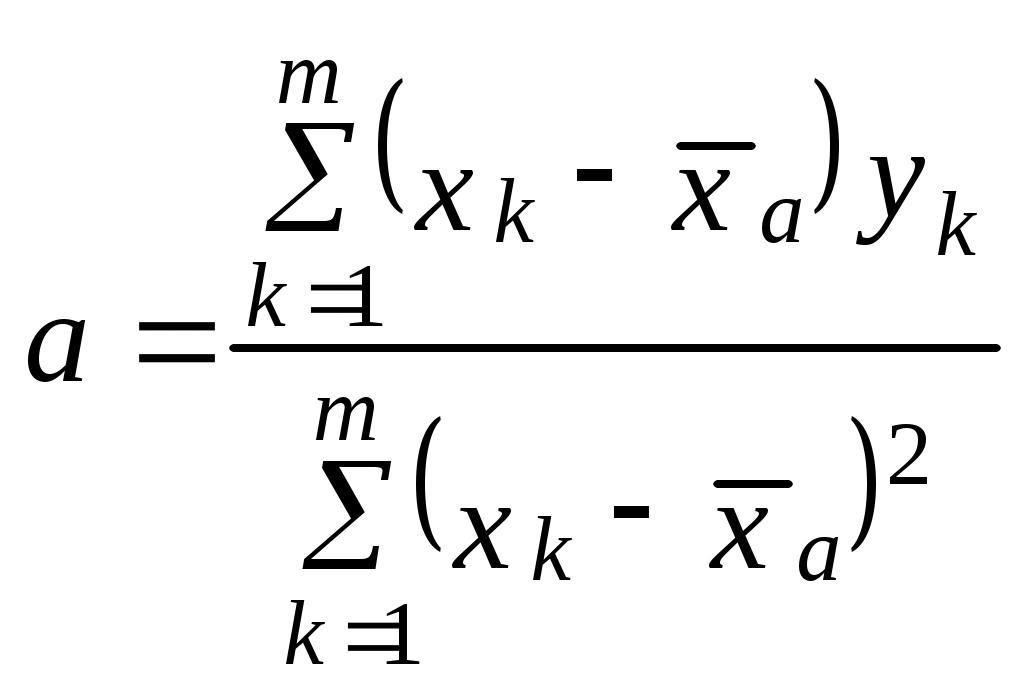

; ; .

Приклад 1. За дослідними даними товарообміну х (тисяч гривень) та витрати обігу у гривнях знайти параметри лінійної залежності y=ax+b.

Х	60	80	140	160	240	320
У	551	576	628,5	673	768,5	863

=60+80+140+160+240+320=1000

=551+576+628,5+673+768,5+863=4080

=60551+80576+140628,5+160673+240768,5+320863=735410

=60²+80²+140²+160²+240²+320²+=215200





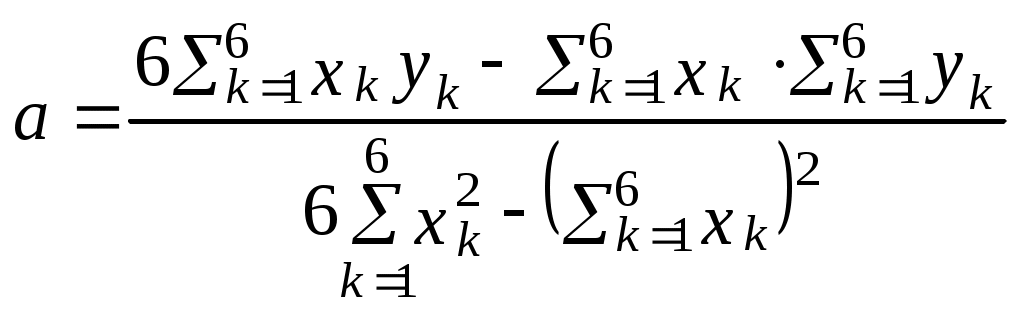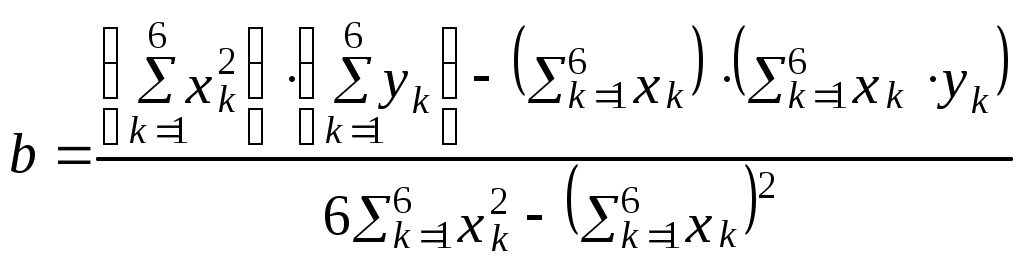y=1,13x+489,71

Кореляція

Якщо лінії регресії У на Х і Х на У– прямі, то кореляцію називають лінійною.

Вибіркове рівняння прямої лінії регресії У на Х:

;

Х на У - ,

де – вибірковий коефіцієнт кореляції .

Зауваження. Якщо дані спостережень задані кореляційною таблицею:

Таблиця.1.

Yj/Xi	X1	X2		Xi		Xm	ni
Y1	n11	n12		n1i		n1m
Y2	n21	n22		n2i		n2m
							
Yj	nj1	nj2		nji		njm
							
Ym	nm1	nm2		nmi		nmm
nj					

то переходять до умовних варіант , ,

де C₁ – для варіант х новий початок відліку;

в якості C₂ зручно приймати варіанту, яка розміщена приблизно в середині варіаційного ряду;

h₁– крок, тобто різниця між двома сусідніми варіантами Х;

C₂ – для варіант У новий початок відліку;

h₂ – крок варіант У.

Приклад 1. За заданою кореляційною таблицею результатів вибірки, ознаки Х,У якої мають нормальний закон розподілу, потрібно записати рівняння прямих регресій

Yj	Xi					ni
5	1	2	2	5	–	10
10	1	1	3	5	–	10
15	2	2	1	25	5	35
20	1	1	4	–	14	20
25	–	4	15	–	6	25
nj	5	10	25	35	25	100

Розв’язок.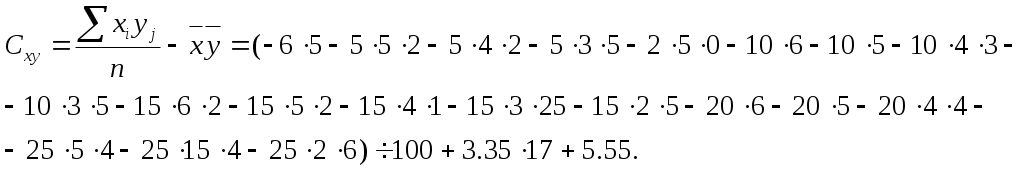

;


;
;
;

;

; ;
; ;

; .

Задачі для самостійного опрацювання

Задача 1. ОБЧИСЛЕННЯ ЙМОВІРНОСТІ ПОДІЇ ЗА КЛАСИЧНОЮ ФОРМУЛОЮ

1.1. Комплект містить 6 виробів 1-го ґатунку, 4 – 2-го ґатунку і 3 браковані вироби. Навмання з комплекту відбирається 5 виробів. Знайдіть імовірність того, що серед вибраних виробів:

а) виявиться 3 вироби 1-го і 2 вироби 2-го ґатунку; б) не виявиться бракованих виробів .

1.2. Сім студентів, серед яких тільки два хлопця, розсаджуються випадковим чином на 7 стільців, розташованих в одному ряду. Знайдіть імовірності подій: а) хлопці зайняли сусідні місця; б) між хлопцями опинилися 3 дівчини.

1.3. Серед 25 фірм, з яких 10 українських, а інші російські, розігрується 5 урядових контрактів. Вважається, що кожна фірма має рівні шанси на отримання контракту. Знайдіть ймовірність того, що:

а) принаймні дві українські фірми виграють контракт; б) тільки дві українські фірми виграють контракт.

1.4. Партія з 12 виробів, серед яких рівно 4 нестандартні, навмання розбивається на дві рівні частини. Знайдіть імовірності подій:

а) в кожній частині буде порівну нестандартних виробів; б) всі нестандартні вироби опиняться в одній частині.

1.5. Із 10 літаків, які прибули до аеропорту протягом доби, 80% мають повне комерційне завантаження. Знайдіть імовірність того, що з п’яти випадковим чином відібраних літаків:

а) всі мають повне комерційне завантаження; б) лише три прибули з повним комерційним завантаженням.

1.6. У фірмі десять співробітників (6 чоловіків і 4 жінки) претендують на заняття трьох вакансій. Вважаємо, що всі кандидатури мають рівні шанси на заняття цих вакансій. Знайдіть ймовірність того, що:

а) жінки не займуть жодної вакансії; б) дві вакансії займуть чоловіки, а одну - жінка.

1.7. Із 15 рейсів, які відправляються з аеропорту N протягом доби, 60% виконується власним літаковим парком. Знайдіть імовірність того, що з п’яти відібраних навмання рейсів власним парком виконується:

а) лише три рейси; б) всі п’ять рейсів.

1.8. 9 осіб займають місця в одному ряду. Знайдіть ймовірність того, що дві певні особи опиняться поряд, якщо:

а) в ряду всього 9 місць; б) в ряду всього 12 місць.

1.9. Комплект містить 7 виробів 1-го ґатунку, 6 – 2-го ґатунку і 2– 3-го ґатунку. Навмання з комплекту вибирається 5 виробів. Знайдіть імовірність того, що:

а) відібрані лише вироби 1-го ґатунку; б) серед відібраних немає виробів 3-го ґатунку.

1.10. Шість літаків, серед яких лише два В-747, виконали посадку в аеропорту і були випадковим чином розподілені на шести стоянках, розташованих в одному ряду. Знайдіть імовірність того, що літаки В-747 опинились:

а) на сусідніх стоянках; б) на крайніх стоянках.

1.11. Серед 15 фірм, з яких 5 українських, а інші російські, розігрується 2 урядових контракти. Вважається, що кожна фірма має рівні шанси на отримання контракту. Знайдіть ймовірність того, що:

а) принаймні одна українська фірма виграє контракт; б) обидва контракти виграють російські фірми.

1.12. В урні знаходяться 15 кульок: 9 білих і 6 чорних. Навмання вийняли 5 кульок. Знайдіть імовірність того, що:

а) вийняли 2 білі та 3 чорні кулі; б) вийняли хоча б одну чорну кульку.

1.13. Комплект містить 6 виробів з номерами від 1 до 6. Випадковим чином по одному з комплекту відбираються всі вироби і розташовуються в один ряд. Знайдіть імовірність того, що:

а) номери виробів розташуються в зростаючому порядку; б) сума номерів виробів, які знаходяться на рівній відстані від кінців ряду, буде однаковою.

1.14. До авіакаси звернулося 3 пасажири, кожен з яких з однаковою ймовірністю може замовити білет на будь-який з шести рейсів, що виконуються протягом дня до аеропорту М. Знайдіть імовірність того, що вони замовили білети:

а) на один рейс; б) на різні рейси.

1.15. Партія з 50 виробів містить 10% браку. З партії навмання вибирають 6 виробів. Знайдіть імовірність того, що серед відібраних виробів:

а) всі якісні; б) лише 2 браковані.

1.16. Комплект містить 7 виробів 1-го гатунку, 6 – 2-го гатунку і два вироби – 3-го гатунку. Випадковим чином з комплекту відбирають 5 виробів. Знайдіть ймовірність того, що: а) серед них не виявиться жодного виробу 3-го гатунку; б) всі 5 виробів – першого гатунку.

1.17. Серед 20 виробів 60% мають вищу якість. Знайдіть ймовірність того, що:

а) три навмання відібрані вироби вищої якості; б) із п’яти відібраних виробів вищої якості хоча б один.

1.18. Комплект складається з десяти виробів, 5 з яких коштують по 4 гривні кожний, 3 – по 2 гривні і 2 – по 3 гривні. Знайдіть імовірність того, що вибрані навмання 2 вироби коштують 6 гривень.

1.19. Партія з 50 виробів містить 30% нестандартних, причому 40% нестандартних виробів є бракованими. Знайдіть імовірності того, що серед відібраних навмання п’яти виробів:

а) лише 3 браковані вироби; б) немає бракованих виробів.

1.20. Нехай 10000 автомобілів мають чотиризначні номери від 00-00 до 99-99.

Знайдіть ймовірність того, що навмання вибраний автомобіль має номер, що:

а) складається з різних цифр; б) утворює число, яке ділиться на 5.

1.21. Партія з 40 виробів містить 15 % браку. З партії навмання вибирають 5 виробів. Знайдіть імовірність того, що серед відібраних виробів:

а) лише 3 браковані; б) 5 виробів якісних і 1 бракований.

1.22. Партія виробів складається з шести виробів першого ґатунку, чотири – другого та двох – третього ґатунку. Навмання з партії відбирається 5 виробів. Знайдіть імовірність того, що серед відібраних:

а) виявиться лише 3 вироби 1-го ґатунку; б) не виявиться жодного виробу третього ґатунку.

1.2322ЦІІФ коштують по 3 гривні кожен, решта по 1 гривні. Знайдіть імовірність того, що відібрані навмання 4 вироби коштують разом 10 гривень.

1.24. В студентській групі навчається 17 хлопців і 9 дівчат. Навмання вибирають 5 студентів. Знайдіть ймовірність того, що серед відібраних буде:

а) тільки 3 хлопці; б) хоча б одна дівчина.

1.25. В комплекті з 40 виробів 30% - нестандартних, причому 50% нестандартних виробів є бракованими. Знайдіть імовірність того, що серед 4-х відібраних навмання виробів буде:

а) лише один бракований; б) усі браковані.

1.26. В комп’ютерному класі знаходиться 10 комп’ютерів з номерами від 1 до 10. Для виконання лабораторної роботи 5 студентів випадковим чином зайняли 5 комп’ют’’’’’’’’’’’’’’’’’’’’’’’’’6ерів. Знайдіть імовірність того, що всі задіяні комп’ютери будуть:

а) з номерами від 1 до 5; б) з послідовними номерами.

1.27. Цифри 1,2,...,9 записують у випадковому порядку. Знайдіть імовірність того, що:

а) всі цифри будуть записані в порядку зростання; б) на парних місцях опиняться парні цифри.

1.28. Комплект складається з 40 виробів, 20% яких – нестандартні. Знайдіть імовірність того, що серед 4-х відібраних навмання виробів:

а) буде однакова кількість стандартних і нестандартних; б) будуть лише стандартні вироби.

1.29. Шість підручників і два задачника випадковим чином розташовані на полиці. Знайдіть імовірність того, що:

а) задачники будуть розташовані поряд; б) між задачниками виявиться два підручника.

1.30. Партія містить 6 виробів першого гатунку, 4 вироби другого і 2 вироби третього гатунку. Навмання відбираються 5 виробів. Знайдіть ймовірність того, що серед них буде:

а) лише 3 вироби першого гатунку; б) 2 вироби першого гатунку і 2 вироби другого гатунку.