Задачи. А це відношення числа випадків

• Название: А це відношення числа випадків
• Анкор: Задачи
• Дата: 26.10.2020
• Размер: 1.39 Mb.
• Имя файла: 91a2f1e933af52685c74dd82a98848c1 (1).doc
• Тип: Документы; #145858
• страница: 2 из 10

Безпосереднє обчислення ймовірностей
Наведемо приклади застосування комбінаторики при розв’язуванні задач класичної теорії ймовірностей.

Приклад 1. Дехто, забувши дві останні різні цифри номера те­лефону, набирає їх навмання. Яка ймовірність зателефонувати адре­сату?

Дві останні і різні цифри можна набрати способами. Шукана ймовірність події А зателефонувати – .

Приклад 2. Яка ймовірність із 5 карток з буквами а, м, р, т, ю, виймаючи їх по одній, утворити слово “юрта”?

Загальне число наслідків випробування – число розміщень із 5 по 4, тобто . Сприятливих наслідків – один. Ящо подія А бажана, то .

Приклад 3. Яка ймовірність із букв а, а, в, к, к, о, х склас­ти слово “Каховка”, беручи їх навмання?

Всіх рівноможливих наслідків стільки, скільки перестановок:

P₇=1·2·3·4·5·6≡5040. Сприятливих наслідків випробування 4, оскільки однакові букви “а” і “к” зустрічаються по два рази, і число їх переставлень не впливає на бажане слово. Отже, .

Приклад 4. Серед N виробів є M бракованих. Беруться навмання n виробів. Обчислити ймовірність, що серед n буде m бракованих виробів.

Зрозуміло, що M ≤ N, m ≤ n. Всіх рівноможливих випадків буде . Нехай А – шукана подія. Зрозуміло, що m бракованих виробів беруться тільки із їх множини М, при цьому – число способів такого вибо­ру. Кожен з цих способів може доповнюватися довільною групою ви­робів із числа способів, якими можна вибрати залишкові (n – m ) придатні із загального їх числа, тобто Таким чином, сприятливе події А число всіх наслідків буде · за правилом добутку в комбінаториці.

На підставі класичного означення ймовірності маємо .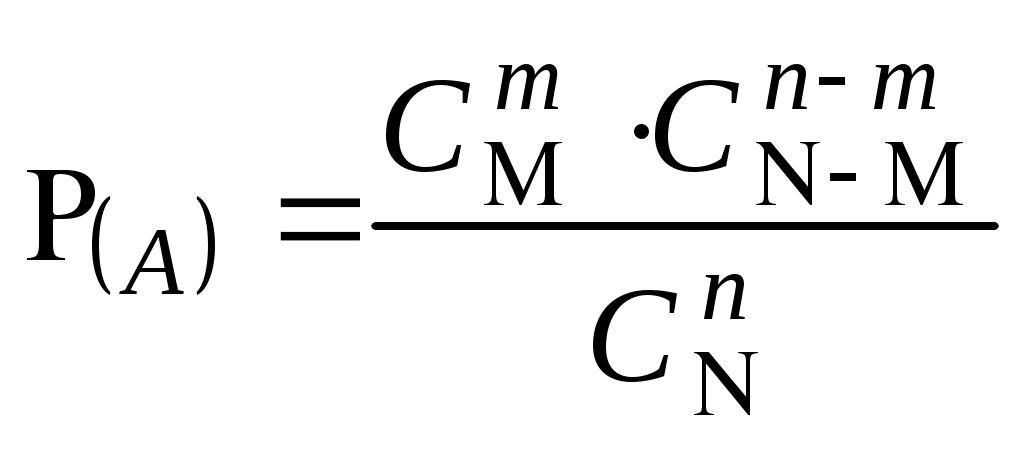

Інший зміст попередньої задачі: в урні N куль, з яких М – білі, решта – чорні. Виймаються n куль. Найти ймовірність, що серед останніх (тобто в n) рівно m білих куль.

Попередній результат запишемо .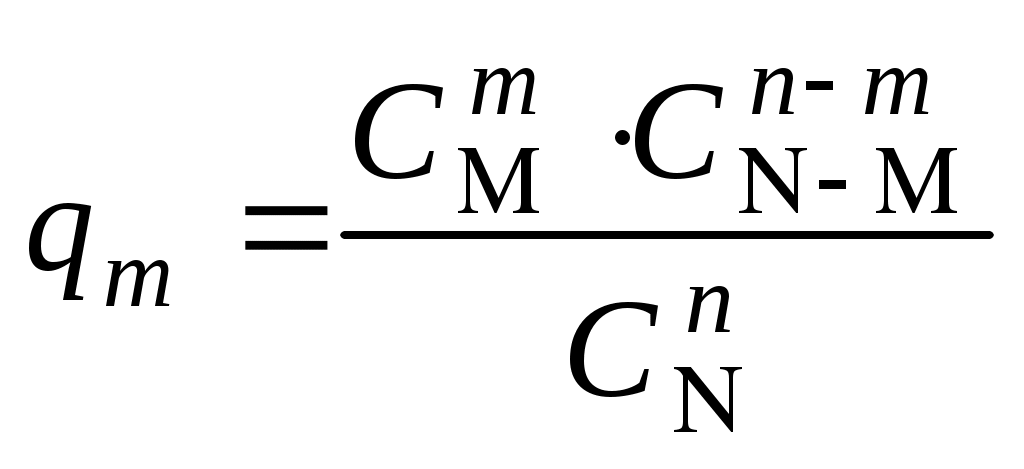

Набір чисел q₀,q₁,…q_m називається гіпергеометричним розподілом.

Як наслідок, запишемо ймовірності вгадати послідовно 3, 4, 5 та 6 цифр, граючи в спортлото 6 із 45: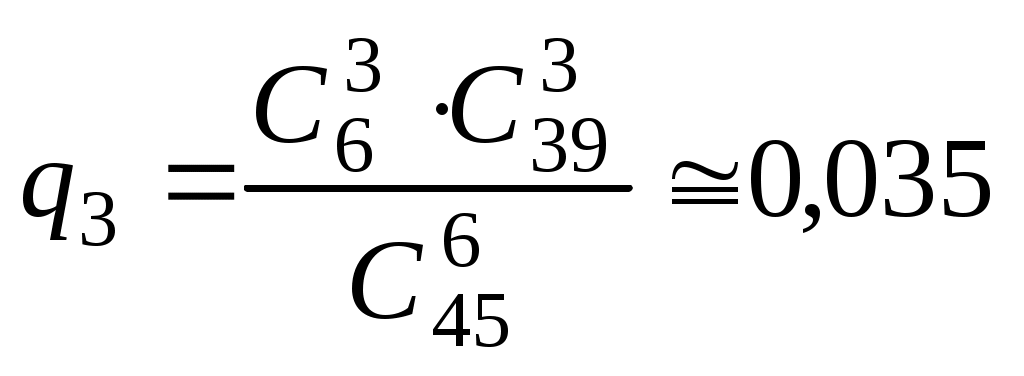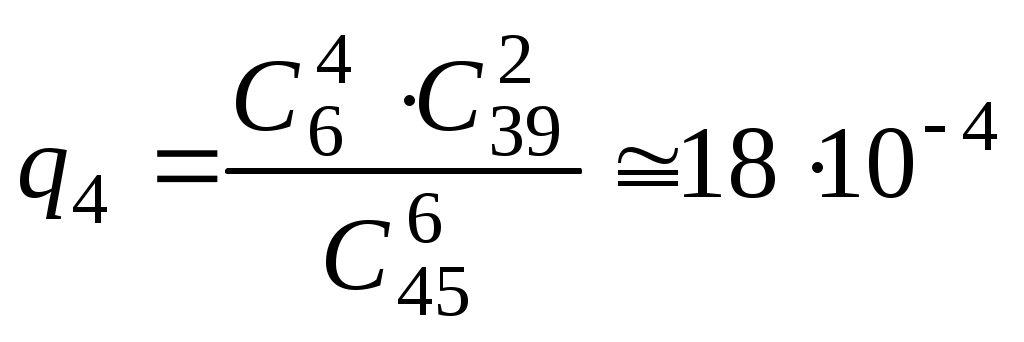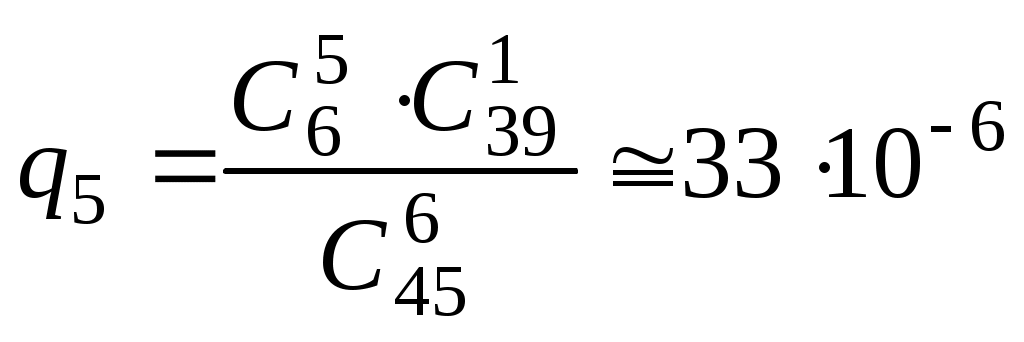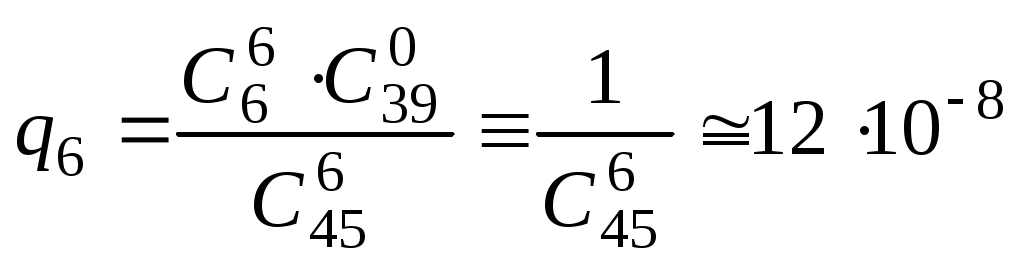

; ;

; .

Приклад 5. Серед 20 лампочок є 5 підвищеної якості. Навмання взяли 7 шт. Яка ймовірність, що серед них будуть 3 лампочки підви­щеної якості?

Загальне число, рівноможливих наслідків

.

Сприятливі наслідки , відбираючи довільні 3 із 5 лампочок підвищеної якості. До кожної трійки додаємо будь-які 4 шт., що беруться із 15 залишкових. Оскільки довільна трійка лампочок підвищеної якості може сполучати­ся з довільною четвіркою, взятою із групи залишкових лампочок, то всіх сприятливих наслідків всього буде .

Шукана ймовірність є: .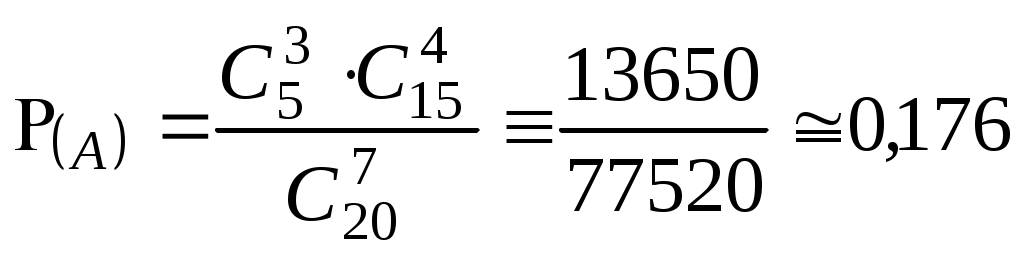

Приклад 6. Із 36 карт навмання беруться 3. Знайти ймовір­ність, що серед них буде один туз. .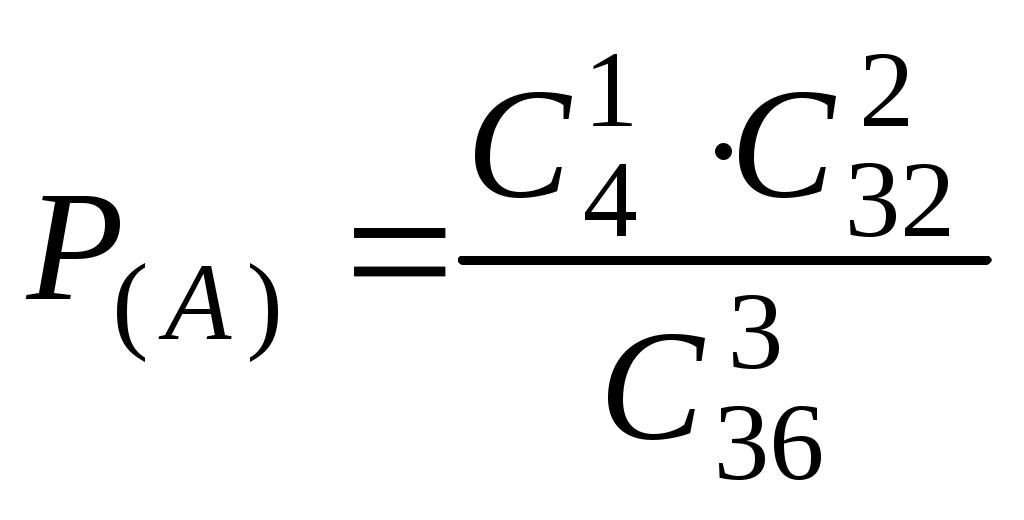

Приклад 7. З якою ймовірністю при виборі навмання 4-х букв із слова “математика” утворюється слово “тема”?

Загальне число рівноможливих наслідків такого випробування . Число сприятливих наслідків рівня 2∙1∙2∙3=12, бо букву “т” можна вибрати 2-ма способами, “е” – одним, “м” – двома, “а” – трьома способами. Шукана ймовірність .

Приклад 8. Із ретельно перетасованих 20 деталей 1-го гатунку та 30 деталей 2-го гатунку беруться навмання 5. Яка ймовірність, що серед них бу­дуть дві деталі 1-го і три 2-го гатунку? .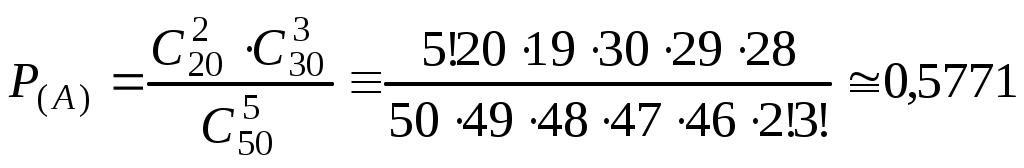

Алгебра подій

П
одією називають результат деякого випро­бування (експеримен­ту, спостереження).

Всякий нерозкладний наслідок експерименту називають елемен­тарною подією W; множина всіх елементраних подій позначається Ω={W}, іменується простором, який зображується на пло­щині прямокутником, причому точки його відповідають елементарним подіям.

Довільна підмножина А простору на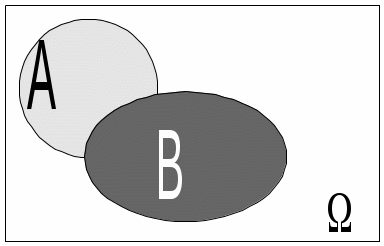зивається подією. Подія А наступає, коли результат експерименту – це одна із елементарних подій, що входить до А, тобто WЄА. Геометрично подія А зобра­жується

є

протилежна до А подія, яка наступає тільки тоді, коли А не відбувається. Якщо при настанні А відбувається подія В, то А В, тобто подія А тягне В.

С умою А + В або об'єднанням А В нази­вається третя подія С =А+ВС = А В, яка наступає тоді і тільки тоді, коли від­бувається хоча б одна подія: А або В. Геометрично сума зображу­ється заштрихованою областю.

Елементарні події входять в А або В, або входять і до А і до В – хоча б одна подія відбувається.

Д 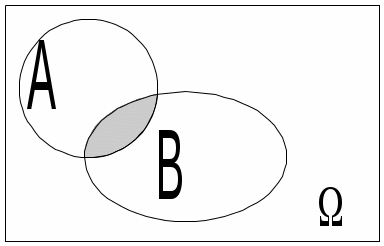обутком АВ (А В) або перетином (перерізом) подій А та В називають подію, що складається з елементарних подій, які входять в обидві події. Зобра­жується геометрично:

П одія, яка проявляється в тому, що А відбу­вається, а подія В ні, називається різницею А–В; її геометрична інтерпретація
А ­– В = А∩ .

Очевидно, що мають місце:

А + = Ω; А = Ø,

де Ø – порожня множина.

Події А₁,А₂,….,Аn утворюють повну групу подій, якщо АiАj = Ø (i≠j) і А1+А2+…+Аn = Ω. Геометричне зображення:

Я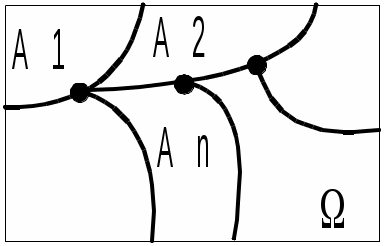
кщо через "+" позначити настання події, а через "–" ні, то операції суми і добутку двох подій зображуються відповідно таблицями:

A	B	A+B		A	B	AB
+	+	+		+	+	+
+	–	+	;	+	–	–
–	+	+		–	+	–
–	–	–		–	–	–

Табличне зображення операцій над подіями використовується для розв’язання задач.
Основні теореми класичної теорії ймовірностей
Теорема 1. Додавання ймовірностей несумісних подій

Ймовірність появи однієї з двох несумісних подій дорівнює сумі ймовірностей цих подій:

P(A+B)= P(A) +P(B).

Наслідок 1. Якщо події протилежні, то сума їх ймовірностей дорівнює одиниці, тобто

P(A)+P( ) =1.
Наслідок 2. Ймовірність появи однієї з декількох попарно несумісних подій дорівнює сумі ймовірностей цих подій.

.

Теорема 2. Додавання ймовірностей несумісних подій

Ймовірність появи хоча б однієї з двох сумісних подій дорівнює сумі ймовірностей цих подій без ймовірності їх сумісної появи.

P(A+B)=P(A)+P(B) P(A∙B)

Зауваження. Теорема може бути узагальнена на довільне скінченне число сумісних подій. Якщо n=3, то

P(A₁+A₂+A₃)=P(A₁)+P(A₂)+P(A₃)–P(A₁A₂)–P(A₁A₃)–P(A₂A₃)+P(A₁A₂A₃).
Приклад 1. Ймовірність того, що куплений товар випущено в Англії – 0,3, а ймовірність того, що товар випущено в Польщі дорівнює 0,6. Яка ймовірність того, що товар випущено в одній із цих країн?

Нехай подія А – товар випущено в Англії, подія В – товар випущено в Польщі, А і В несумісні. Застосувавши теорему додавання ймовірностей несумісних подій, маємо

Р(А+В) = Р(А) + Р(В) =0,3 + 0,6 = 0,9
Приклад 2. Один лотерейний білет виграє з ймовірністю 0,0003. Яка ймовірність того, що володар одного білету нічого не виграє?

Нехай подія А – виграш. Тоді означає, що білет не виграє. Події А і протилежні. Використовуючи наслідок 1, маємо

Р( ) = 1 – Р(А) = 1 0,0003 = 0,9997.
Приклад 3. Ймовірність отримання кредиту для першої особи дорівнює 0,6, а для другої – 0,5. Визначити ймовірність того, що принаймні одна особа отримає кредит.

Введемо позначення: подія А₁ – перша особа отримує кредит; подія А – друга особа отримує кредит. Тоді А₁+А₂ є подією “принаймні одна особа отримує кредит”. Р(А₁)=0,6; Р(A₂)=0,5. Враховуючи, що події А₁ і А₂ можуть відбуватися одночасно, і використовуючи теорему про ймовірність сумісних подій, маємо:

Р(А₁+A₂)=Р (А₁)+(A₂)–P(А₁A₂)=0,6+0,5–0,3=0,8.
Теорема 3. Множення ймовірностей незалежних подій

Ймовірність сумісної появи двох незалежних подій дорівнює добутку ймовірностей цих подій:

Р((А∙В)=Р(А)∙Р(В).
Узагальнення. Ймовірність появи кількох подій, незалежних в сукупності, дорвінює добутку ймовірностей цих подій:

Р((А₁∙А₂∙А₃∙А_n)= Р(А₁)Р(А₂)Р(А₃)∙…∙Р(А_n).
Теорема 4. Множення ймовірностей залежних подій

Ймовірність сумісної появи двох залежних подій дорівнює добутку ймовірностей однієї з них на умовну ймовірність іншої:

Р(АВ)=Р₂ (А) ∙Р_A (В).
Узагальнення. Ймовірність сумісної появи кількох залежних подій дорівнює добутку ймовірностей однієї з них на умовні ймовірності всіх інших, причому ймовірність кожної наступної події обчислюється в при­пущенні, що всі попередні події уже відбулися:

Р(А₁∙А₂∙А₃∙…∙А_n)= Р(А₁)Р (А₂)Р (А)₃∙…∙Р (А_n).
Приклад 4. Прилад, що працює протягом доби , складається з трьох вузлів, кожен з яких незалежно від інших може за цей час вийти з ладу. Якщо не працює хоча б один з вузлів, то прилад теж не працює. Ймовірність безвідмовної роботи протягом доби першого вузла дорівнює 0,9, другого – 0,85, третього – 0,8. Чому дорівнює ймовірність того, що протягом доби прилад працюватиме безвідмовно?

Нехай подія А_i буде і=1, 2, 3 означає, що і-тий вузол справний; подія А – прилад протягом доби працює безвідмовно. Враховуючи, що прилад працює безвідмовно тоді, коли справні всі три вузли, тобто А=А₁ А₂ А₃, та те, що події А₁ А₂ А₃ незалежні у сукупності, маємо:

Р(А)=Р((А₁∙А₂∙А₃)= Р(А₁)Р (А₂)Р(А₃)=0,9∙0,85∙0,8=0,612
Приклад 5. Тривалими спостереженнями встановлено, що приблизно 90 % підприємств перевіряються податковою інспекцією протягом певного терміну. Із загальної кількості перевірених у 40 % знаходять певні пору­шення. Знайдіть ймовірність того, що певне підприємство перевірять і знайдуть певні порушення.

Введемо позначення. Події А та В відповідно “дане підприємство перевіряють”, “знайдено певне порушення”. Тоді Р(А)=0,9, Р_A(В)=0,4. Вра­ховуючи, що події А і В залежні, використаємо теорему множення ймо­вірностей залежних подій:

Р(АВ)= Р(А)Р_A(В)=0,9 ∙0,4=0,36.
Теорема 5. Ймовірність появи хоча б однієї події

Ймовірність появи події А, яка відбувається внаслідок появи хоча б однієї з подій А₁, А₂,…А_n, незалежних в сукупності, дорівнює різниці між одиницею і добутком ймовірностей протилежних подій :

Р(А)=1-Р( .
Зауваження. Якщо всі n-подій мають однакову ймовірність, рівну р, то ймовірність появи хоча б однієї події дорівнює:

Р(А)=1–qⁿ.