Задачи. А це відношення числа випадків

• Название: А це відношення числа випадків
• Анкор: Задачи
• Дата: 26.10.2020
• Размер: 1.39 Mb.
• Имя файла: 91a2f1e933af52685c74dd82a98848c1 (1).doc
• Тип: Документы; #145858
• страница: 6 из 10

Розв’язання. Об’єм вибірки n=1+4+2+6+7=20.

Знайдемо відносні частоти:



Контроль: 0,05+0,2+0,1+0,3+0,35=1.
Розподіл відносних частот записується

xi	5	7	8	10	12
Wi	0,05	0,2	0,1	0,3	0,35

Інколи відносні частоти виражаються у процентах.

Приклад 2. Заводським відділом технічного контролю при пере­вірці деякого розміру деталей отримано таку таблицю розподілу деталей:

Варіанти	Абсолютні частоти (число деталей)
11.30	1
11.32	8
11.34	17
11.36	26
11.38	36
11.40	44
11.42	34
11.44	17
11.46	6
11.48	1

Знайти розподіл частот в процентах.

Розв’язання. Загальне число деталей вибірки:

n=1+8+17+26+36+44+34+17+6+1=190

Домножуючи відносні частоти на 100 %, отримуємо бажаний результат:

W₁= %=0,53%; W₆= %=23,16%;

W₂= %=4,21%; W₇= %=17,85%;

W₃= %=8,95%; W₈= %=8,95%;

W₄= %=13,68%; W₉= %=3,15%;

W₅= %=18,95%; W₁₀= %=0,53%.

Запишемо отримані частоти в початкову таблицю:

Відносні частоти (в процентах)
0,53
4,21
8,95
13,68
18,95
23,16
17,85
8,95
3,15
0,53

Контроль:20,53+4,21+8,95+13,68+18,95+23,16+17,85+8,95+3,15=99,96%.
Емпірична функція розподілу

Емпірична функція розподілу визначається як ,

де n_x – число всіх варіант, менших х.

Емпірична функція F(x) є неспадаючою. Вона наближено зображує інтег­ральну функцію F(x)=P(X
Приклад 1. Для даного розподілу

Xi	2	5	7
Ni	4	16	20

Знайти емпіричну функцію і побудувати її графік.

Розв’язання. Об’єм вибірки є n=4+16+20=40. Найменша варіанта x₁=2, тому F(x)=0 при х≤2. Значення х<5, тобто варіанта x₁=2, спостерігалось 4 рази. Отже,

.

Для значення х<7 маємо дві варіанти x₁=2, і x₂=5, які спостерігались n₁+n₂=20 разів.

Тому .

Оскільки x=7 – найбільша варіанта, то F(x)=1 при x>7.

Емпірична функція F(x) приймає вигляд: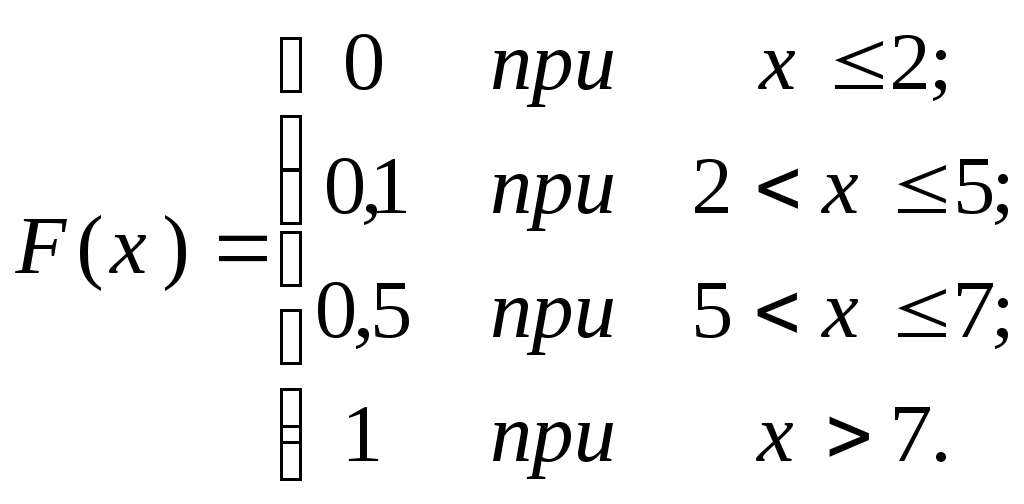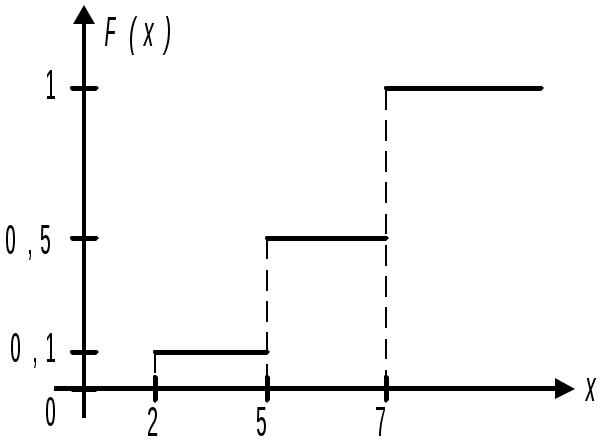




Її графік наведено на рисунку 1.
Рис. 1
Графічне зображення статистичних розподілів
При незначному числі варіант використовують полігон: ламана, відрізки якої з’єднують точки (x₁;n₁), (x₂;n₂), …, (x _k;n _k), називається полігоном частот. Якщо точки мають координати (x_i;w_i), то буде полігон відносних частот.

Гістограмою частот називають ступінчасту фігуру, що складається з прямокутників, основами яких є частинні інтервали довжини h=x_i-x_i-1, а висотами відношення (щільність частоти).

Площа гістограми висот дорівнює об’єму вибірки.

Приклад 1. За даними таблиці результатів випробування міцності ниток побудуйте полігон.

Міцність нитки	120-140	140-160	160-180	180-200	200-220
Кількість ниток n	1	4	10	14	12

Розв’язання. Даний інтервальний ряд перетворимо в дискретний, обчисливши значення ознаки, що припадає на середину.

Міцність нитки	130	150	170	190	210
Кількість ниток n	1	4	10	14	12

Будуємо точки, координатами яких є пари чисел з дискретного варіаційного ряду (130; 1), (150; 4) і т.д., сполучивши утворені точки (130; 1) (270; 1) з серединами найближчих інтервалів (110; 0) (230; 0)

Приклад 2. Магазин протягом місяця реалізував 100 пар жіночого взуття. Розподіл його за розмірами подано в таблиці. Побудувати гістограму.

Розмір	33-35	35-37	37-39	39-41
Кількість пар	12	36	44	8

Розв’язання. Побудуємо на осі абсцис інтервали довжини h=2. Над цими інтервалами паралельно осі ОХ проводимо відрізки на висоті, рівній відповідній щільності частоти. Наприклад, для інтервалу 33-35 маємо від­різок, паралельний осі абсцис на висоті в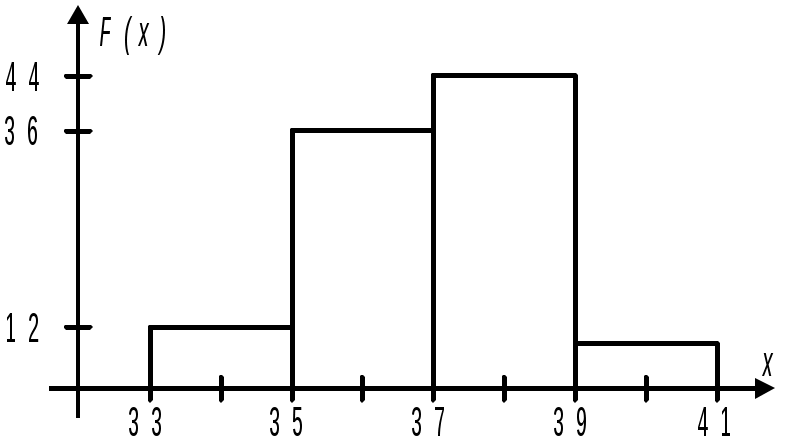ід ОХ.

С
татистичні оцінки параметрів розподілу

Точковими оцінками є:

– вибіркова середня:

;

– вибіркова дисперсія:

.

Зауваження. Степеневою середньою вибірки називають:

;

– при =1 одержимо вибіркову середню, а

– при =2 – середньоквадратичну вибірки:

;

– при =–1 одержимо середню гармонічну: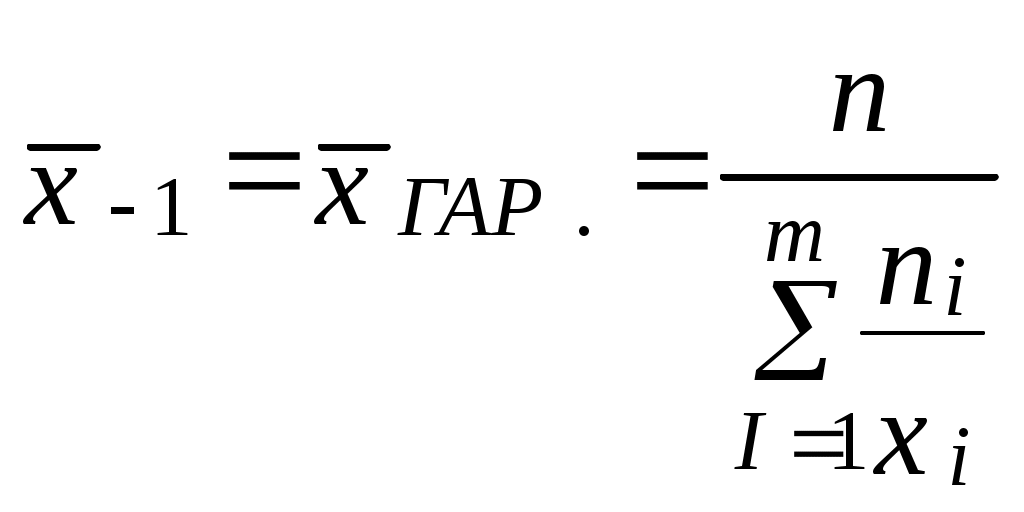

;

– при =0 одержимо середню геометричну:

, де х_і>0.

Для обчислення дисперсії Д_В частіше використовують формулу:

.

Вибірковим середньоквадратичним відхиленням називають:

.

Виправлена вибіркова дисперсія є:

²;

відповідно – виправлене середньоквадратичне відхилення вибірки.

Приклад 1. Вибіркова сукупність задана таблицею.

хі	5	8	10	11	14
ni	2	3	6	4	1

Знайти числові характеристики.

Розв’язання. Будуємо допоміжну таблицю.

хі	ni	nixi	xi2	nixi2
5	2	10	25	50
8	3	24	64	192
10	6	60	100	600
11	4	44	121	484
14	1	14	196	196
n=16	16	152		1522

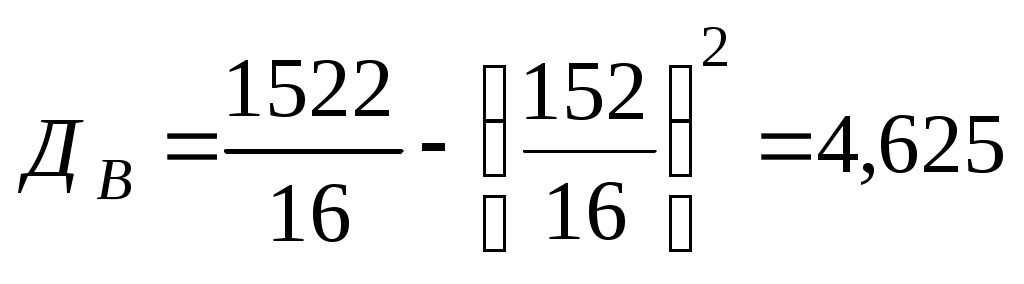Приклад 2. Обчислити середнє квадратичне відхилення вибірки, заданої розподілом.

хі	0	2	5
nі	3	5	2

Запишемо розподіл х².

хі2	0	4	25
ni	3	5	2

.

Зауваження 1. Якщо початкові варіанти х_і – великі числа то для спрощення обчислень зручно відняти від кожної з варіант одне й те ж число С, тобто перейти до умовних варіантів u_i=x_i-C ; .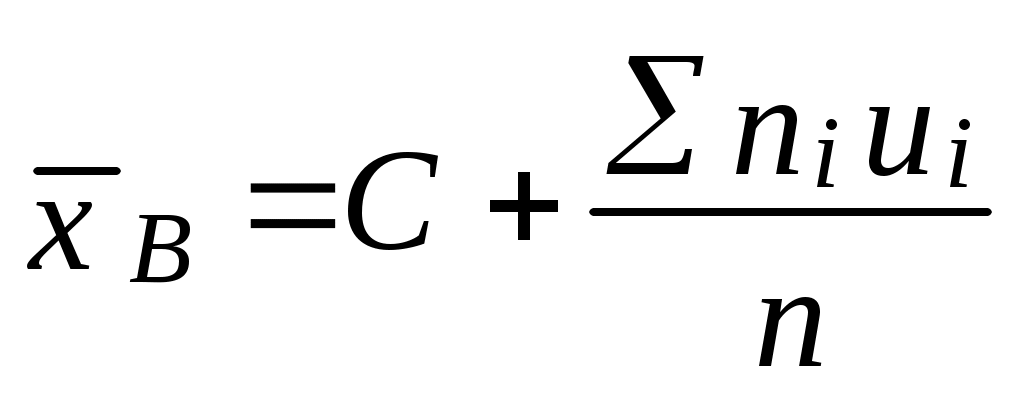

Зауваження 2. Якщо початкові варіанти є десятковими дробами з k-десятковими знаками після коми, то зручно перейти до умовних варіант u_i=Сx_i (при цьому дисперсія збільшиться в С² раз):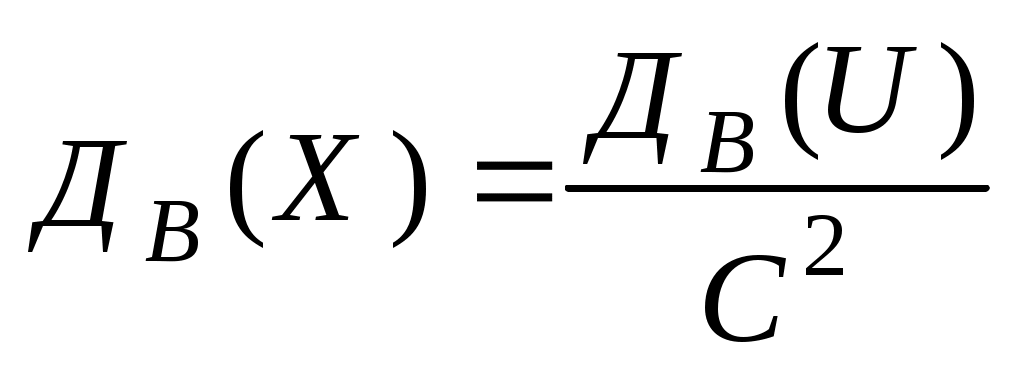

.

Незміщеною оцінкою генеральної дисперсії є виправлена вибіркова дисперсія: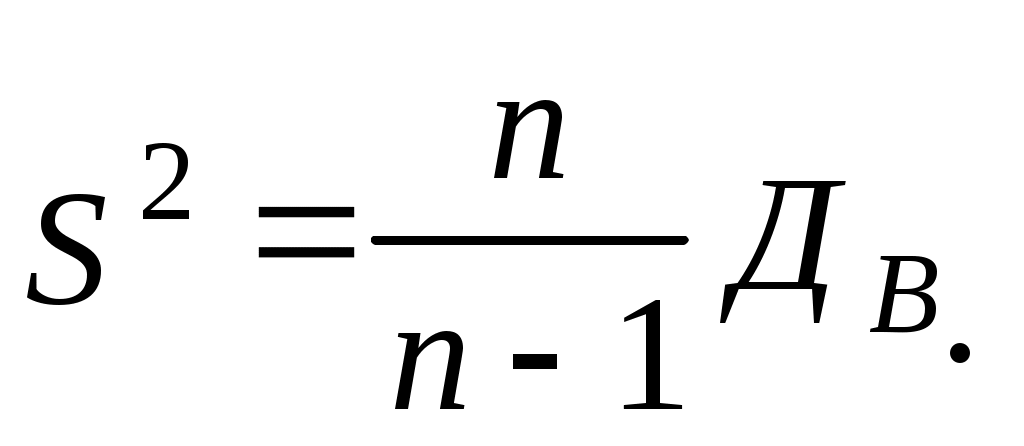


Інтервальна оцінка визначається двома точками – початком і кінцем інтервалу.

Інтервал (називають довірчим, якщо він покриває невідо­мий параметр із заданою надійністю P(^<).

Для оцінки математичного сподівання а-нормально розподіленої кількісної ознаки Х за вибірковою середньою ; якщо відомо середнє квадратичне відхилення генеральної сукупності, служить довірчий інтервал:

,

де – точність оцінки;

n – об’єм вибірки;

t – аргумент функції Лапласа, для якого Ф(t)= 

Якщо невідоме і об’єм вибірки n>30, то використовують подвійну нерівність:

,

де S – виправлене середнє квадратичне відхилення;

t_знаходять за таблицею для заданих n і .

Для оцінки середнього квадратичного відхилення нормально роз­поділеної кількісної ознаки Х з надійністю  за виправленим вибірковим середнім квадратичним відхиленням S використовуються довірчі інтервали:

S(1-q)<
0<1,

де q знаходять за таблицею, маючи задані n і .

Об’єм вибірки n, ; ,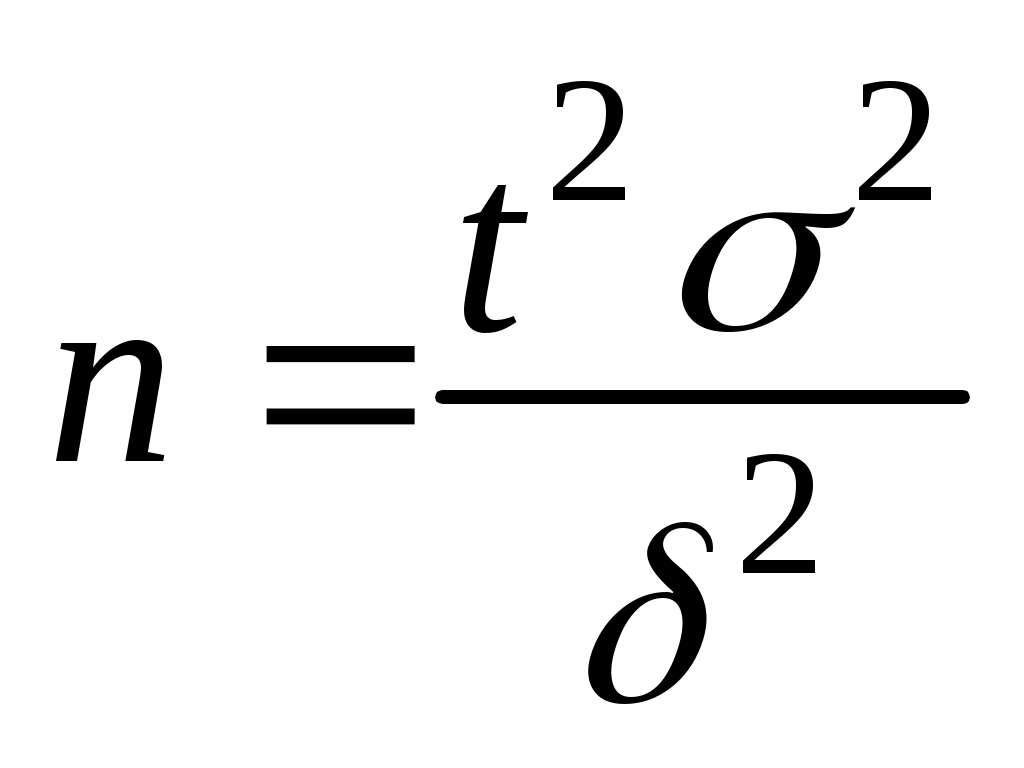

Розглянемо приклади застосування інтервальних оцінок.