Задачи. А це відношення числа випадків
 Скачать 1.39 Mb. Скачать 1.39 Mb.
|
|
Числові характеристики неперервних випадкових величин (НВВ) У випадку НВВ математичне сподівання, дисперсія та середнє квадратичне відхилення мають той самий зміст і ті самі властивості, але вираховуються за іншими формулами. Якщо f(x) – щільність розподілу ймовірності Х, тоді М(Х) знаходять за формулою: Дисперсія, як і у випадку ДВВ, обчислюється за формулою: D(X) = M((X - M(X))2), що у випадку НВВ має вигляд: Для розрахунку зручно використовувати формулу: Середнє квадратичне відхилення НВВ визначають таким чином: Основними законами розподілу НВВ є рівномірний, показниковий, нормальний та розподіл Стьюдента. Випадкова величина Х розподілена рівномірно у проміжку [a;b], якщо її щільність ймовірності має вигляд: 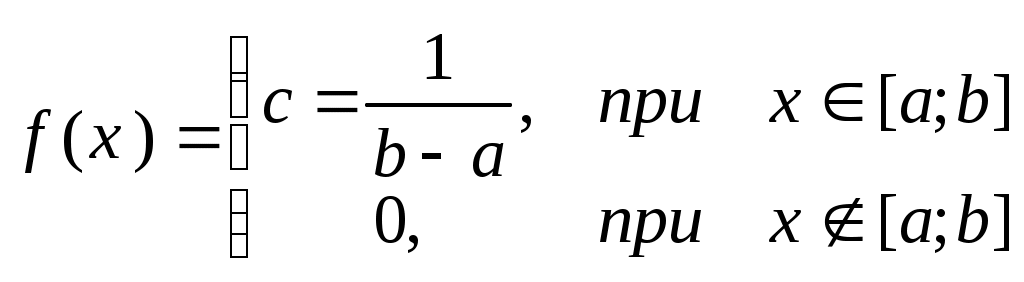 (4) (4)Числові характеристики НВВ Х, що рівномірно розподілена: Ймовірність того, що рівномірно розподілена ВВ Х потрапить в проміжок [x1;x2] за умови a≤x1<x2≤b вираховується за формулою: Випадкова величина Х розподілена за показниковим законом з параметром , якщо щільність її ймовірності має вигляд: Числові характеристики НВВ Х, що має показниковий розподіл, визначаються: Інтегральна функція розподілу для ВВ Х, що має показниковий розподіл, задається формулою: 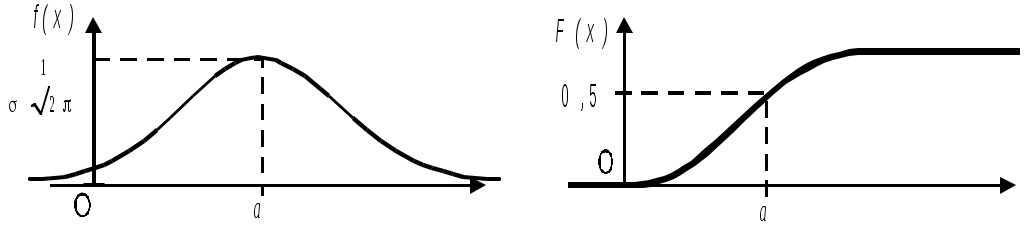 (9) Ймовірність того, що розподілена за показниковим законом BB Х потрапить в інтервал (a;b) за умови 0 Р(a НВВ Х розподілена за нормальним законом, якщо щільність її ймовірності має вигляд: 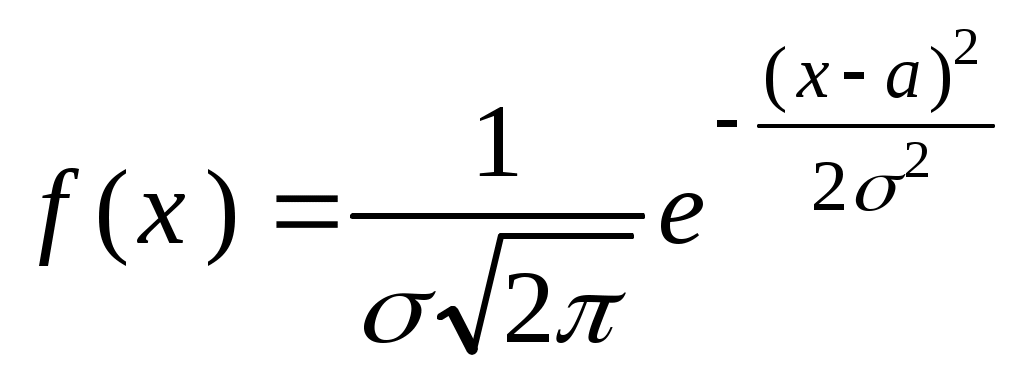 , (11) , (11)де a та – параметри розподілу. Графік цієї функції називається нормальною кривою або кривою Гаусса. Інтегральна функція нормального розподілу має вигляд: 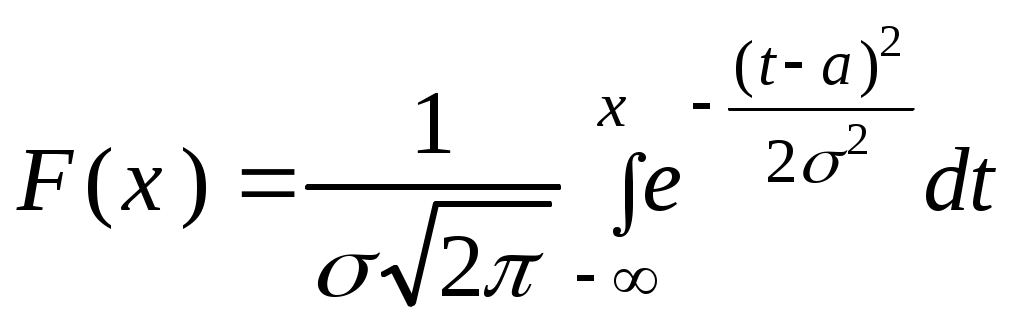 (12) або (12) або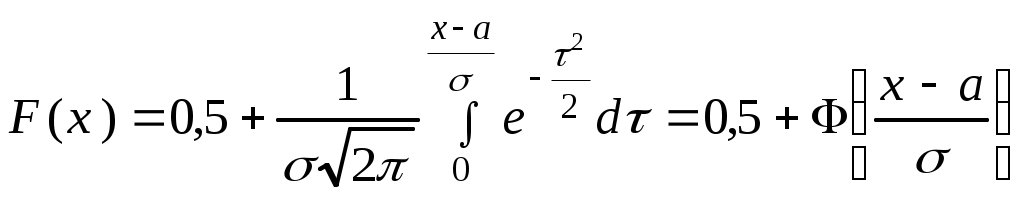 (13) (13)При а=0; =1 нормальна крива називається нормованою та НВВ Х має нормований нормальний розподіл. Числові характеристики НВВ Х, що розподілена за нормальним законом: М(Х)= а; D(X) =2. (14) Ймовірність того, що нормально розподілена величина потрапить в проміжок (c;d): де Ф(х) – функція Лапласа, що задається формулою Для обчислення ймовірності відхилення нормально розподіленої ВВ від свого математичного сподівання а на наперед задану величину використовують формулу: Графіки функцій f(x) та F(x), що задані формулами (11), (12) мають вигляд: “Правило трьох сигм”. Якщо ВВ Х розподілена нормально, то ймовірність того, що абсолютна величина відхилення Х від її математичного сподівання прямує до 0, тобто подія |X–a|<3, практично достовірна. Випадкова величина Т має розподіл Стьюдента (t-розподіл) з k ступенями свободи, якщо її щільність ймовірності має вигляд: Коефіціент Ck визначається з умови Числові характеристики ВВ Т, що має розподіл Стьюдента, є : М(Т)=0; При зростанні k розподіл Стьюдента швидко наближається до нормального розподілу. Цей розподіл табульований і досить широко використовується в математичній статистиці та економетриці. Приклад 1. Знайти числові характеристики ВВ Х, що задана функцією розподілу: 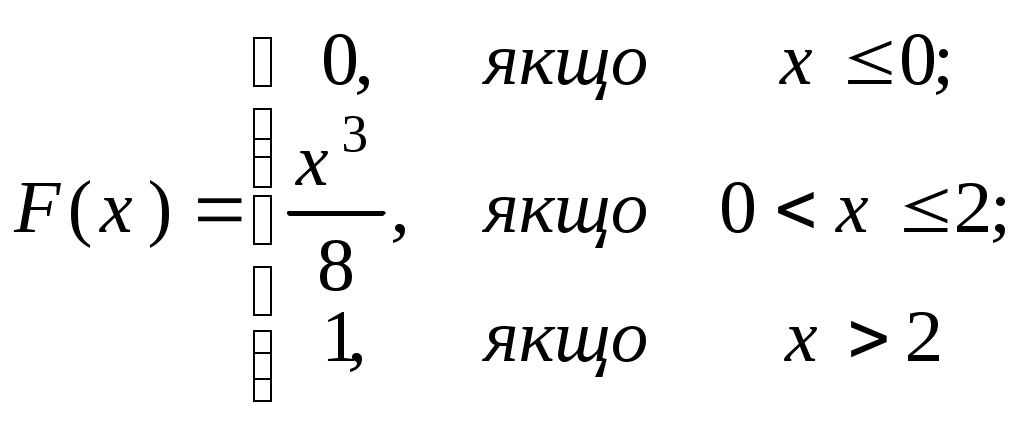 Розв’язання. Знайдемо щільність ймовірності за формулою f(x) = F(x): 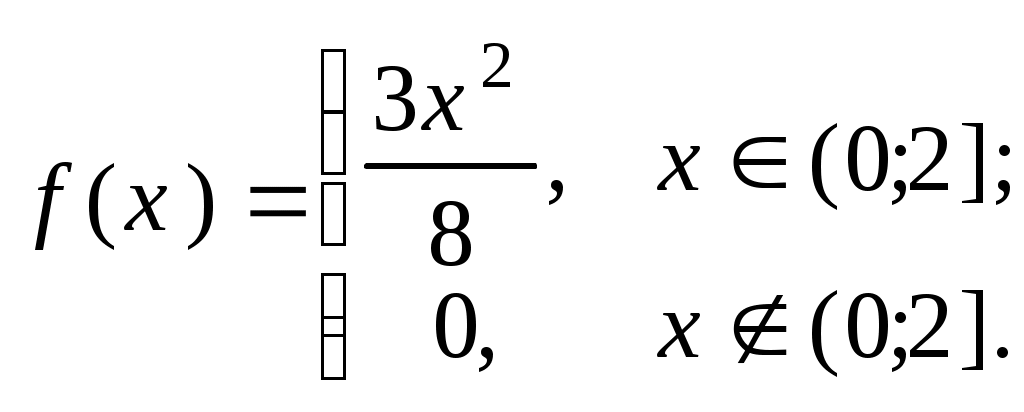 За формулою (1) знайдемо математичне сподівання: 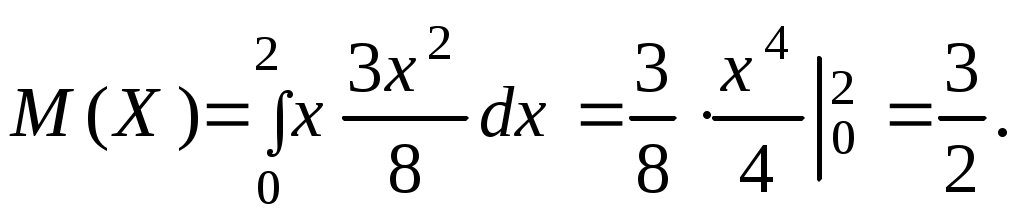 Дисперсію знайдемо за формулою (2): Середнє квадратичне відхилення знайдемо за формулою (3): Приклад 2. Випадкова величина рівномірно розподілена на проміжку [3;18]. Знайти М(Х),D(X), (X), побудувати графіки функцій f(x) та F(x), обчислити ймовірності подій Р(4<Х<10) та Р(Х<12). Розв’язання. Згідно з формулами (4)-(6) і враховуючи, що 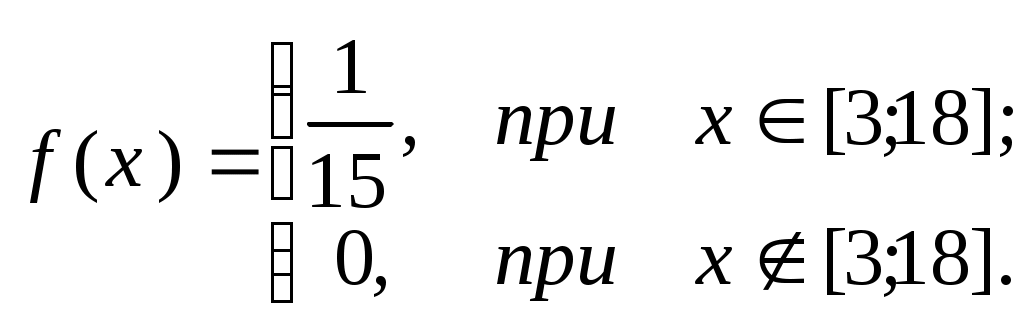 ; ; 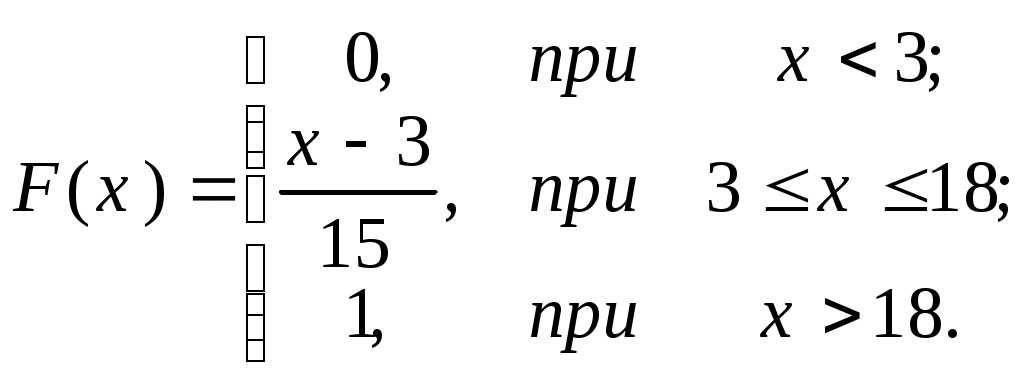 Г 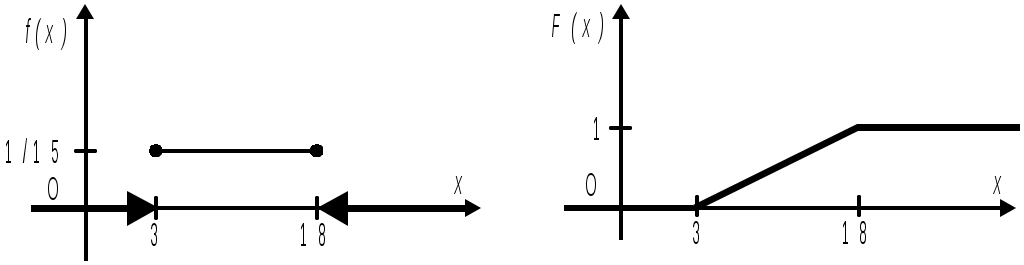 рафіки функцій f(x) та F(x) мають вигляд Приклад 3. Величина Х розподілена за законом: Знайти М(Х), D(X), (X), Р(0,2 Розв’язання. Задана випадкова величина має показниковий розподіл з параметром =5. Згідно з формулами (8) – (10) і враховуючи,що F(x)=P(X<x) та Р(Х≥х)=1–F(x), маємо: Приклад 4. Статистичні дослідження показали, що річний прибуток працівника страхового бізнесу має нормальний розподіл з середнім значенням 8000 гривень і середньо-квадратичним відхиленням 1000 гривень. Навмання відібрано особу, що працює в страховому бізнесі. Яка ймовірність того, що її річний прибуток буде: а) менше, ніж 6000 гривень; б) не менше, ніж 10000 гривень; с) між 7500 та 9200 гривень. Розв’язання. а) ймовірність Р(Х<6000) обчислимо за формулою (13): 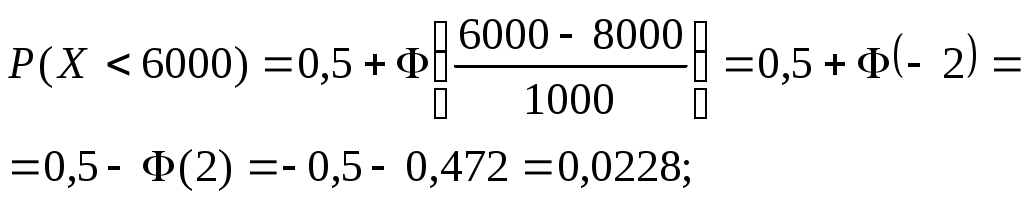 б) ймовірність Р(Х 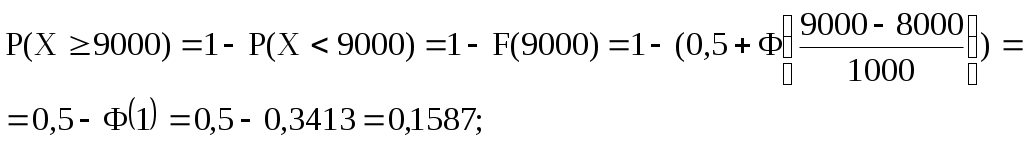 в) ймовірність Р(7500 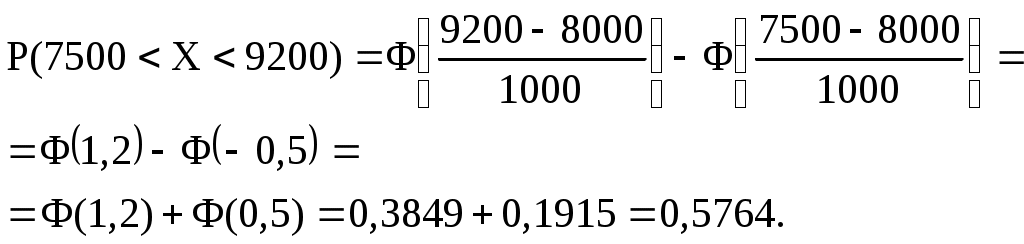 Приклад 5. Відбувається зважування певної речовини без системних помилок. Випадкові помилки зважування мають нормальний розподіл з середньоквадратичним відхиленням =20 г. Знайти ймовірність того, що зважування буде виконано з похибкою, яка за абсолютною величиною не перебільшує 10 г. Розв’язання. Нехай Х – випадкова помилка, за умовою задачі Х нормально розподілена з М(Х)=а, (Х)=20. Використаємо формулу (17) при =20; =10, маємо: Закон великих чисел Лема Чебишова. Якщо ВВ Х, для якої існує математичне сподівання М(Х), приймає лише невід’ємні значення, то для будь-якого додатнього числа має місце нерівність: Нерівність Чебишова. Якщо Х – ВВ з математичним сподіванням М(Х) та дисперсією D(X), то для будь-якого >0 має місце нерівність: Теорема Чебишова (Закон великих чисел). Нехай Х1, Х2,...Хn,... послідовність незалежних випадкових величин з одним і тим самим математичним сподіванням m та дисперсіями, що обмежені однією і тією самою константою c. Тоді для будь-якого >0 має місце нерівність: Доведення теореми базується на нерівності: 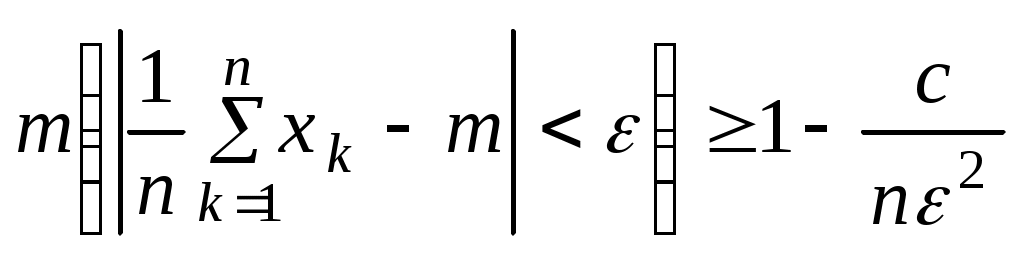 (4) (4)Наслідком ЗВЧ є теорема Бернуллі. Теорема Бернуллі. Нехай відбувається n-незалежних випробувань, в кожному з яких з ймовірністю p може відбутись деяка подія А. Нехай n – випадкова величина, що дорівнює числу появ події А в цих n випробуваннях, тоді для будь-якого >0 сравджується: Нерівність (4) за умов теореми Бернуллі записується наступинм чином: Узагальнена теорема Чебишова. Якщо Х1, Х2,...Хn,... послідовність випадкових величин з математичними сподіваннями М(Х1)=m1, M(X2)=m2,... та дисперсіями, що обмежені однією і тією ж постійною величиною с, то для будь-якого >0 справджується: 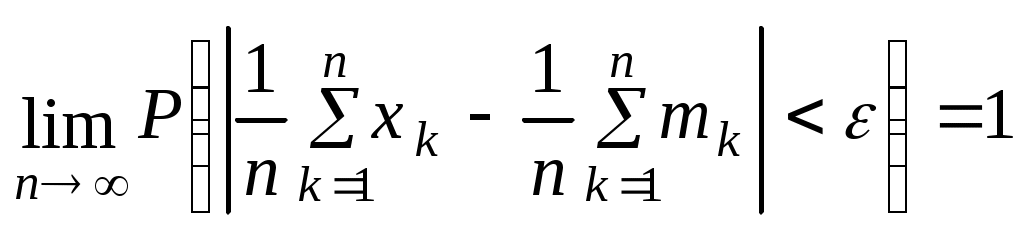 . (7) . (7)Приклад 1. Оцінити ймовірність того, що з 800 малих підприємств збанкрутіє не менше 50, якщо ймовірність банкрутства будь-якого навмання взятого малого підприємства постійна і рівна 0,05. Розв’язання. Нехай Х – число збанкрутілих підприємств. Ця ВВ підпорядковується біномному розподілу з параметрами n=800; p=0,05. Тоді згідно з формулою обчислення математичного сподівання ВВ, що має біномний розподіл, маємо: M(X)=np=8000,05=40. Використаємо нерівність (1) при =50: Приклад 2. Середня температура в приміщенні в період опалювального сезону дорівнює 20о С, а середнє квадратичне відхилення дорівнює 2о С. За допомогою нерівності Чебишова оцінити знизу ймовірність того, що температура в квартирі відхилиться від середньої менше, ніж на 4о С. Розв’язання. Нехай ВВ Х – температура в приміщенні. За умови М(Х)=20; (X)=2. З нерівності (2): Приклад 3. Ймовірність того, що телевізор витримає гарантійний термін роботи дорівнює 0,95 для всіх 200 телевізорів, які обслуговує гарантійна майстерня. Оцінити ймовірність того, що число телевізорів, які витримають гарантійний термін роботи, буде в межах [185;195]. Розв’язання. ДВВ Х – число телевізорів, які витримають гарантійний термін роботи, має біномний розподіл ймовірності, тому M(X)=np=2000,95=190; D(X)=npq=2000,050,95=9,5; =195–190=|185–190|=5 і використаємо нерівність Чебишова у формулі (2). Вибірковий метод Є одним із найважливіших методів статистики. Він дозволяє на підставі вибіркової сукупності отримати висновок про числові характеристики генеральної сукупності. Статистичний розподіл вибірки Варіанти хі ознаки Х генеральної сукупності, записані в зростаючому порядку, утворюють варіаційний ряд. Таблиця
де ni – число повторень (частота) кожної варіанти, називається статистичним розподілом. Сума всіх частот 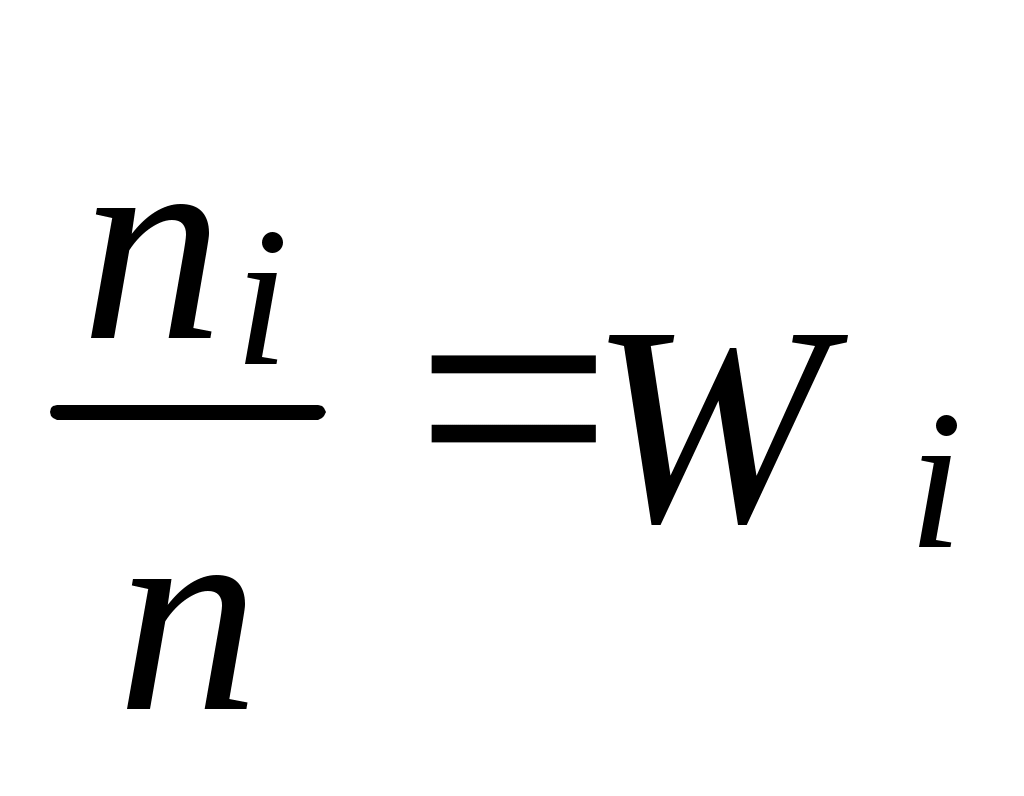 називається відносною частотою (частістю). називається відносною частотою (частістю).Приклад 1. Для вибірки
Записати розподіл відносних частот. |
