Метод виклад з мат-ки 2. Спеціальна методика викладання математики зміст методика розв'язування арифметичних задач
 Скачать 7.16 Mb. Скачать 7.16 Mb.
|
|
У першому числі є одиниці всіх розрядів, у другому - немає одиниць першого розряду, а у третьому - відсутні одиниці другого розряду. Якщо у числі відсутній якийсь розряд (або розряди), на їхньому місці ставлять нулі. При читанні чисел назви пропущених розрядів не вказуються. Наприклад, сто двадцять, двісті чотири. Зрозуміло?" Учні креслять таблицю розрядів у зошитах, записують числа і читають їх. Продовжити роботу над утворенням і записом неповних трицифрових чисел можна на числових таблицях. Наприклад, дається завдання скласти числа з круглими сотнями і десятками; круглими сотнями та одиницями і записати їх: 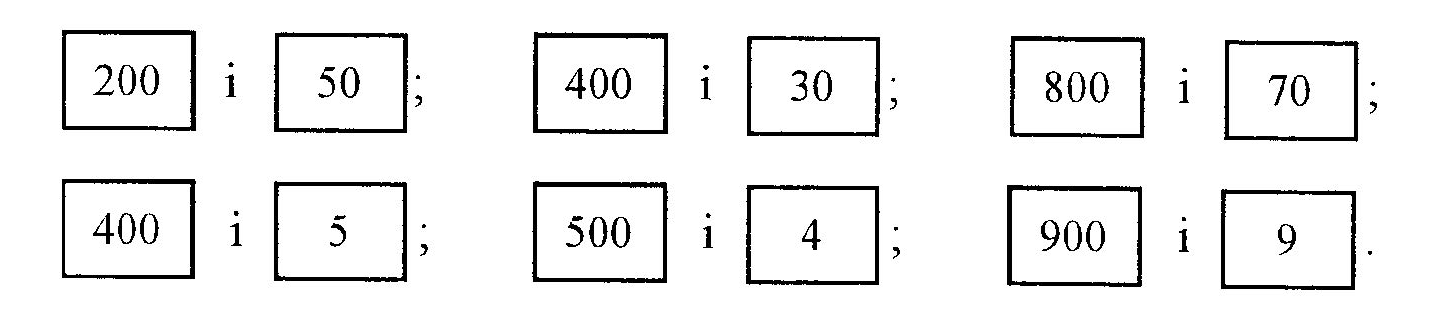 Після того, як учні навчилися утворювати повні і неповні трицифрові числа, читати і записувати їх, вони переходять до роботи над закріпленням послідовності натурального ряду чисел. їм потрібно показати, що числа і після 100 також утворюються за допомогою додавання до попереднього числа одиниці або віднімання від наступного одиниці. Пояснення проводиться у формі бесіди з використанням наочності. Для цього вчитель пропонує школярам відрахувати 10 паличок і зв'язати їх у пучок - десяток, потім відрахувати 10 пучків і зв'язати їх у пучок - сотню, після чого повідомляє: "Давайте візьмемо одну сотню паличок і додамо до них ще одну паличку. Це буде сто і одна паличка, або сто одна паличка. Додамо ще одну паличку, буде сто і дві палички, або сто дві палички. До ста двох паличок додамо ще одну паличку, буде сто три палички. Будемо і далі додавати по одній паличці і отримуємо таку кількість: сто чотири, сто п'ять, сто шість, сто сім, сто вісім, сто дев'ять. Якщо ж до ста дев'яти додати ще одну паличку, отримаємо число сто десять. Це яскраво видно на рисунку 7.1." Рисунок 7.1 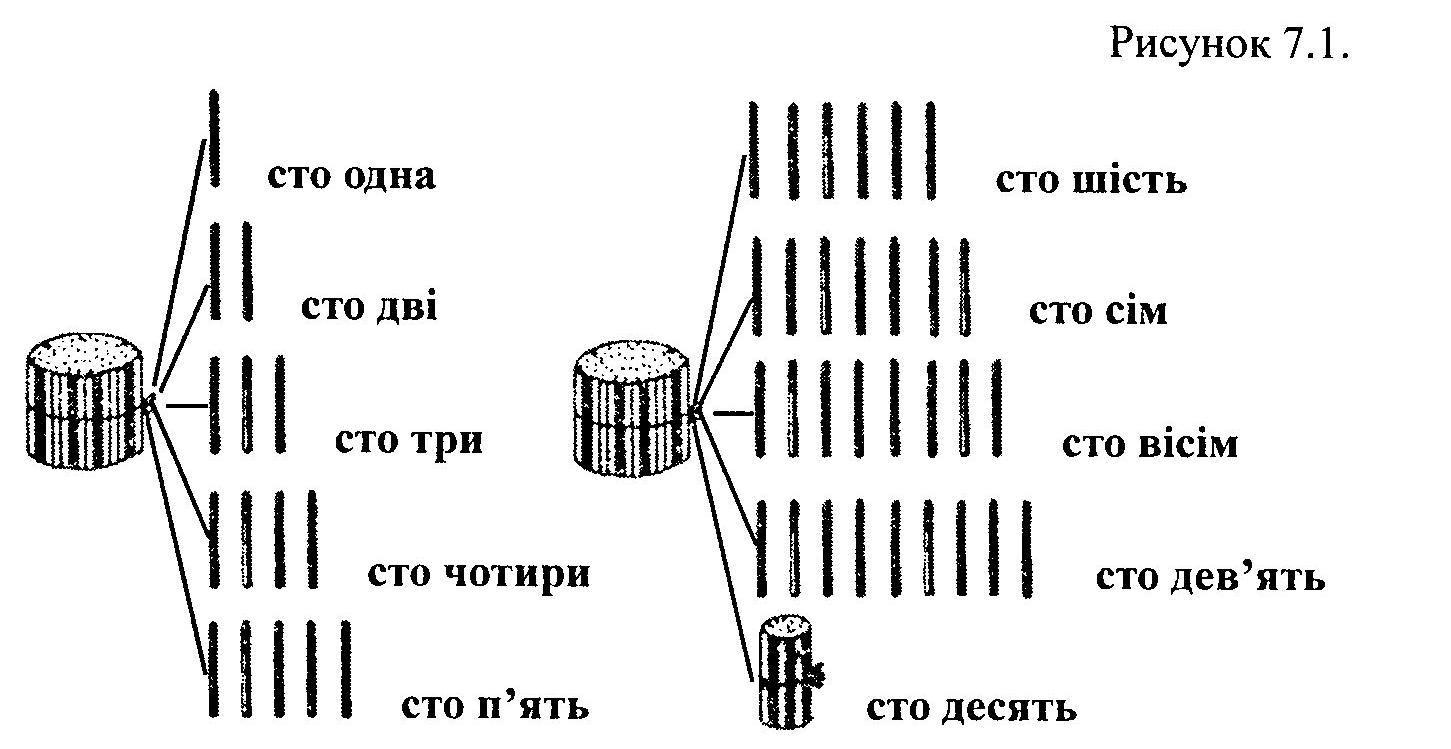 Таким чином, рахунок ведеться до числа 199. Утворення нової сотні пояснюється так: вчитель бере сто паличок (1 пучок - сотню), дев'ять десятків (9 пучків - десятків) і дев'ять одиниць і до останніх додає 1 паличку. Отримані десять одиниць замінюються одним десятком. Проводиться рахунок: 1 сотня і 10 десятків. 10 десятків - це сто, або 1 сотня. Отже, утворилась нова сотня. Значить!00 та ще 100 — буде 200. Можна записати: 100 + 100 = 200. Проводиться рахунок як у прямому, так і у зворотному порядку в межах 200. Аналогічно учні знайомляться з утворенням чисел від 201 до 300; від 301 до 400, ..., від 901 до 1000. Але проводити всю цю роботу на уроці недоцільно, бо школярі будуть втрачати багато часу. Запис чисел від 1 до 1000 краще проводити поступово, наприклад, спочатку написати числа першої сотні, потім другої і так далі у квадратах книжки "Тисяча". Більша частина цієї роботи може проводитись не на уроках, а під час підготовки домашніх завдань. На уроках математики учні проводять рахунок від заданого числа до заданого. Обов'язково потрібно включати вправи на рахунок з переходом до нового десятка або сотні. Наприклад, порахувати від 239 до 241; від296 до 309 тощо. Після таких вправ діти ведуть рахунок одиницями, десятками, сотнями і рівними числовими групами. Рахунок по одному проводиться в певних рамках. Школярам пропонується порахувати по одному від 588 до 602, від 896 до 905; від 101 до ПО, назвати 5 чисел, які стоять за числом 297; порахувати у зворотному напрямку від 803 до 795. Потім продовжується рахунок десятками (ПО, 120, ..., 200), сотнями (100, 200,300...), групами по 200, (200, 400, 600, 800, 1000), по 250 (250, 500, 750, 1000), по 50 і т.д. Деякі учні не зможуть рахувати абстрактно, тому їм необхідно дозволити користуватися наочністю. Рахунок у зворотному порядку значно складніший для розумово відсталих учнів, а значить і тут потрібно прибігати до наочності. Так, для того, щоб порахувати від 200 до 195, учень бере 2 пучки - 2 сотні паличок, одну сотню паличок він розв'язує і отримує 1 сотню і 10 десятків паличок. Потім розв'язує 1 пучок - 1 десяток і починає віднімати по 1 паличці: "У мене є 1 сотня 9 десятків і 10 паличок, я беру одну паличку і отримую - 1 сотню 9 десятків 9 паличок, тобто число 199. Від цього числа знов віднімається 1 одиниця, отримуємо число 198", і так до 195. Результати утворення чисел за рахунок додавання і віднімання по одиниці можна записувати у зошитах, наприклад: 240 + 1 = 241 300 + 1 = 301 999 + 1 = 1000 241 – 1 = 240 301 – 1 = 300 1000 – 1 = 999 Закріпленню знань про десятковий склад числа допоможуть вправи на додавання і віднімання типу 200 + 40 + 5; 450 – 400; 450 – 50; на заміну даного числа сумою розрядних доданків: 453 = 400 + 50 + 3 або розрядними одиницями. Гарним наочним посібником тут може служити картка з розрядними числами: При вивченні усної нумерації діти вчаться встановлювати загальне число одиниць (десятків і сотень), наявних у числі. Розумово відсталі слабко диференціюють схожі за звучанням питання. Для них однаково звучать запитання: "Скільки одиниць в числі?" і "Скільки всього одиниць в числі?". Тому вироблення в них цього поняття значно ускладнюється. Опираючись на наочність, школярам спочатку дається поняття загальної кількості десятків у числі. Так, наприклад, у числі 746 є 4 десятки. Далі береться один великий пучок (сотня) і уточнюється, що в ньому 10 десятків. Значить, у 7 сотень буде 10 дес. х 7 = 70 дес. Таким чином, у числі 746 - всього 74 десятки. Провівши декілька таких вправ, учитель звертає увагу дітей на те, що кількість десятків у числі можна визначити, якщо закрити розряд одиниць. Число, яке залишилося і вказує на кількість у ньому десятків. Аналогічно проводиться пояснення всієї кількості одиниць у числі. Спочатку учням пропонується визначити кількість одиниць у двоцифровому числі. Так, учислі 46-6 одиниць, у 1 дес. - 10 одиниць, значить, у 4 дес. буде 10 дес. х 4 = 40 од. Отже, у числі 46 всього 46 одиниць. Далі береться трицифрове число: 746. У ньому 6 одиниць, а в 4 дес. буде (10 од. х 4) 40 одиниць; 1 сотня має 100 одиниць, значить, у 7 сотнях буде (100 од. х 7) 700 одиниць. Отже, у числі 746, яке містить у собі сотні, десятки та одиниці, всього буде 746 одиниць. Такі вправи допомагають значно прискорити вироблення навичок диференціації понять "Скільки одиниць в числі?" і "Скільки всього одиниць в числі?" Одним з етапів при вивченні нумерації є порівняння чисел. Учням даються завдання називати число, на одиницю більше (менше) від даного; збільшити (зменшити) число на одиницю; визначити більше (менше) число за кількістю сотень, десятків, одиниць. Наприклад, з кожної пари чисел назвати більше (менше) число: 235 і 236; 140 і 1394; 360 і 306; 500 і 600; 430 і 413. Ефективність процесу порівняння чисел розумово відсталими учнями можна значно підвищити, якщо використовувати розрядну таблицю: Таблиця 7.3.
Важливо навчити учнів порівнювати числа, які складаються з одних і тих самих цифр, але які розташовані у різних розрядах: 1, 10, 100, 1000; 5, 50, 500. Використовуючи розрядну сітку, учні наочно переконуються в тому, що кожне наступне число у 10 разів більше попереднього.
На етапі вивчення нумерації чисел в межах першої тисячі доцільно познайомити учнів і з поняттям "Клас одиниць". їм повідомляється, що одиниці, десятки і сотні об'єднуються в окремий клас – клас одиниць. Це перший клас. (При вивченні багатоцифрових чисел вони познайомляться з другим класом - класом тисяч). На дошці вчитель креслить розрядну сітку, яку діти перемальовують до себе в зошити, вписує в неї трицифрові числа і під час аналізу за їхнім десятковим складом знайомить з класом і записує його над розрядами.
Ця таблиця допомагає учням визначити всю кількість одиниць у числі, вірно записати числа (під диктовку чи з підручника) і при цьому звернути особливу увагу при записі на ті з них, у яких є нуль в середині або в кінці числа. Школярів потрібно навчити робити аналіз числа з визначення класу. Закріплення нумерації чисел в межах 1000 продовжується і під час вивчення арифметичних дій. Потрібно зауважити, що при вивченні усної нумерації в межах 1000 розумово відсталі учні знайомляться з прийомами заокруглення чисел до круглих десятків. При цьому дітям пояснюється, що при округленні числа потрібно відкинути одиниці (якщо в кінці його стоять цифри 1, 2, 3, 4) і залишити це ж число, лише з 0 на кінці, наприклад: 262 заокруглюємо до 260; 364 заокруглюється до 360 і т.д. У випадку, якщо в кінці числа стоять числа 5, 6, 7, 8, 9 заокруглення призводить до збільшення числа на 1 десяток і на їхньому місці записати число з 0 на кінці, наприклад, число 826 округлюємо до 830; 278 до 280. У 5-му класі учні знайомляться з римською нумерацією від І до XII. Формування знань про римську нумерацію потрібно пов'язати з місяцями. Учні вже знають, що числа в межах 1000 записуються за допомогою 10 знаків. Тепер вони вивчають 12 чисел, які позначаються трьома знаками -І, V та X. Щоб записати римські цифри за допомогою цих трьох знаків, потрібно вимагати від розумово відсталих учнів усвідомлення такого правила: якщо І стоїть перед V або X (з лівої сторони) - вона віднімається, якщо після (з правої) - додається: IV – 4; VI – 6, IX – 9. 7.3. Обчислення прикладів на додавання і віднімання в межах тисячі При обчисленні прикладів без переходу через розряд використовуються усні обчислювальні прийоми, а з переходом через розряд - прийоми письмових обчислень. У першому випадку запис вирішення прикладу проводиться з записом у штику, у другому - в стовпчик. Розглянемо етапи вивчення додавання і віднімання в межах 1000. 1. Додавання і віднімання без переходу через розряд. а) додавання і віднімання круглих сотень. 100+100; 200 – 100; 200 +100; 300 – 100. Ще під час вивчення нумерації учні практикувались у рахунку сотнями, тому цей тип прикладів для обчислення не є складним. Вирішення їх зводиться до рахунку і виконання арифметичних дій в межах 10. Наприклад: 200 + 100. Міркування проводиться з використанням наочності. Вчитель пише на дошці число 200. Бере два пучки – 2 сотні паличок і рахує: "Одна сотня та ще одна сотня, отримали дві 2 сотні. Це 200. Потім бере ще 1 пучок - сотню і рахує загальну кількість пучків-сотень: 2 сот. + 1 сот. = 3 сот. З сотні це – 300. Таким чином: 200 + 100 = 300. Аналогічні міркування проводяться і при обчисленні прикладів на віднімання. Для того, щоб вирішити приклад 300-100, необхідно 300 показати як 3 сотні, а потім від 3 сотень відрахувати 1 сотню. 300 – 100 = 300 = 3 сот. : 100 = 1 сот. 3 сот. – 1 сот. = 2 сот. = 200 Щоб полегшити учням засвоєння цих прийомів доцільно пропонувати вирішувати аналогічні приклади з числами в межах 10,100, 1000 з наступним співставленням компонентів і результатів дій. Це приклади типу: 6+2= 8–3= 60 + 20= 80–30 = 600 + 200= 800 – 300 = б) додавання і віднімання круглих сотень з однозначними числами; круглих сотень з десятками. а) 400 + 6 = 406 – 6 = 6 + 400 = 406 – 400 = 6) 300 + 50 = 350 – 50 = 50 + 300 = 350 – 300 = в) 500 + 45 = 545 – 45 = 45 + 500 = 545 – 500 = Дані випадки розглядаються як нумераційні, адже суму або різницю в них знаходять виходячи з розуміння того, як утворюються трицифрові числа з розрядних одиниць, тобто з сотень, десятків і одиниць. в) додавання і віднімання круглих десятків, круглих сотень і десятків. а) 540 + 30 б) 570 + 300 в) 540 + 130 570 – 130 610 – 130 870 – 300 За своєю складністю ці приклади умовно діляться на три групи і роботу з ними потрібно починати з урахуванням рівня складності. Обчислення прикладів типу а) зводяться до додавання і віднімання двоцифрових чисел, що виражають число десятків. 540 + 30 = 540 = 500 + 40 500 + 40 + 30 = 570 У даному прикладі перший доданок розкладаємо на розрядні одиниці, а далі виконуємо обчислення спочатку десятків, а потім сотень і десятків. Потрібно зазначити, що при обчисленні прикладів ми завжди повинні показувати зв'язок нових алгоритмів обчислень з уже відомими. При вирішенні прикладів на віднімання міркування проводиться аналогічно. При додаванні і відніманні трицифрових чисел і круглих сотень (приклади типу б) можна використати декілька прийомів. 1) Міркування проводиться і в першому випадку: 570 – 300 = 270 570 – це 5 сот. і 7 дес. 300 – це 3 сот. 5 сот. – 3 сот. = 2 сот. Додаємо залишок і отримаємо: 2 сот. + 7 дес. = 2 сот. 7 дес. = 270. 2) У другому випадку перший доданок або зменшуване потрібно розкласти на розрядні одиниці: 570 + 300 = 870 570 – 300 = 270 570 = 500 + 70 570 = 500 + 70 500 + 300 = 800 500 – 300 = 200 800 + 70 = 870 200 + 70 = 270 3) Найпростішим прийомом є підкреслення тих розрядів, над якими будуть проводитись обчислення: 570 + 300 = 870 570 – 300 = 270 На наступному етапі розглядається обчислення прикладів типу в), алгоритми роботи над ними ґрунтуються на розкладанні другого доданка або від'ємника на розрядні одиниці. 540 + 130 = 540 – 130 = 130 = 100 + 30 130=100 + 30 540 + 100 = 540 540 – 100 = 440 540 + 30 = 570 440 – 30 = 410 д) додавання до трицифрових чисел одно-, дво- і трицифрових чисел та відповідні випадки віднімання. а) 243 + 3; 6)243 + 40; в) 430+24, 454 + 24; г) 450+134. 245 – 3; 245 – 30; 283 – 40, 434 – 24; 589 – 134. Прийоми додавання і віднімання прикладів типу а) полягають в тому, що арифметичні дії проводяться між розрядами одиниць на основі знань нумерації і арифметичних дій між числами в межах 10. В основі алгоритмів обчислення прикладів типу б) і в) лежать прийоми виконання дій 1–го ступеня в межах 100. Додавання і віднімання прикладів типу г) вимагає розкладання другого доданка або від'ємника на розрядні одиниці і застосування прийомів усного обчислення. 450 + 134= 589 – 134 = 134 = 100 + 30 + 4 134 = 100 + 30 + 4 450 + 100 = 550 589 – 100 = 489 550 + 30 = 580 489 – 30 = 459 580 + 4 = 584 459 – 4 = 455 д) додавання і віднімання трицифрових чисел з нулем в середині або в кінці числа: а) 507 + 231; 6) 405 – 302; в) 547 – 204. З прийомами обчислення прикладів даних типів учні вже знайомі. При цьому розкладати доданок або від'ємник не обов'язково. 507 + 231 = 405 – 302 = 547 – 204 = 507 + 200 = 707 405 – 300 = 105 547 – 200 = 347 707 + 30 = 737 105 – 2 = 103 347 – 4 = 343 737 + 1=738 е) додавання і віднімання нуля і віднімання трицифрових чисел, коли в остачі зачитається нуль: 0 + 234; 500 – 0; 456 – 456. Перш ніж давати учням для обчислення приклади цього типу, необхідно повторити з ними утворення числа 0 з застосуванням наочності. Наприклад, запропонувати їм визначити, скільки кружечків залишилося: 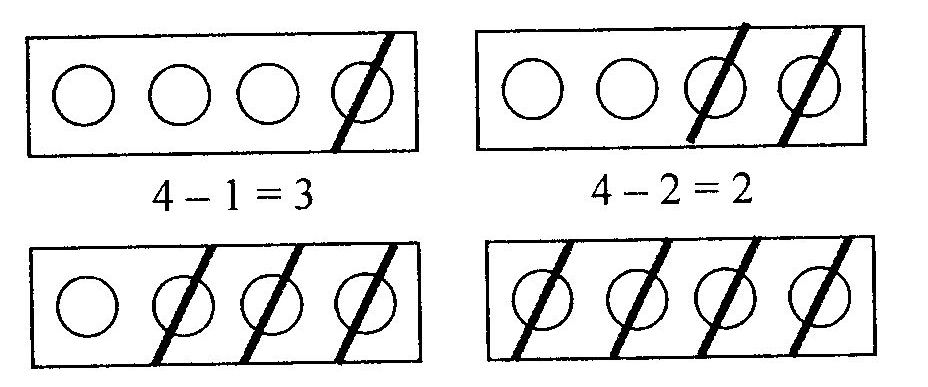 Учнів підводять до висновку, що при відніманні рівних чисел дістаємо нуль. Уточнюється місце 0 в числовому ряді. Для закріплення пропонується виконати обчислення ще декількох прикладів даного типу: 1 – 1 = 0 3 – 3 = 0 5 – 5 = 0 4 – 4 = 0 7 – 7 = 0 8 – 8 = 0 Далі вчитель відтворює в пам'яті дітей додавання і віднімання • нуля. Він запитує у них, що зображено на рисунку зліва? (Пуста ваза). Що зображено на рисунку справа? (Ваза з п'ятьма яблуками).  Математично це можна написати так: 0 + 5 = 5 Аналогічна робота проводиться і на других малюнках. Перед тим, як приступити до вивчення додавання і віднімання з переходом через розряд, учнів потрібно познайомити з записом трицифрових чисел у стовпчик. На додавання даються приклади без переходу через розряд в розряді одиниць, десятків і сотень, на віднімання - коли кожен розряд зменшуваного більше відповідних розрядів від'ємника. Але спочатку приклади вирішуються прийомами усних обчислень, в лінійку: 275 + І23 = 753 – 412 = 123 = 100 + 20 + 3 412 = 400+10 + 2 275 + 100 = 375 753 – 400 = 353 375 + 20 = 395 353 – 10 = 343 395 + 3 = 398 343 – 2 = 341 Учням пояснюється, що виконання прикладів таким шляхом дуже громіздке і що є більш легкий спосіб - запис у стовпчик. При цьому вчитель повинен зазначити, що правильна відповідь може бути отримана лише при правильному записі розрядних одиниць. Потрібно запам'ятати, що одиниці записуються під одиницями, десятки під десятками, сотні над сотнями. Між числами зліва ставиться знак (+) при додаванні або (-) при відніманні. 275 _753 + 123 412 398 341 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
