fnpQ>
т. е. формулу прежней структуры (4.8). Коэффициент пропорциональности /пр в этой формуле называют приведенным коэффициентом трения. Он всегда больше фактического коэффициента тренияf. Так, например, при а = 15° отношение^ //= 7,66. Во столько же раз увеличивается суммарное нормальное давлениеQ'z по сравнению с силой прижатия катков Q и уменьшается нагрузка на валы и подшипники.
Фрикционные передачи применяют в приводах небольшой мощности, в частности в конструкциях вариаторов — устройствах для бесступенчатого изменения скорости вращения ведомого катка, одна из конструктивных схем которого представлена на рис. 4.5. Вариатор представляет собой двухступенчатую фрикционную передачу, в которой промежуточный каток является одновременно ведомым для первой ступени и ведущим — для второй. В соответствии с формулой (4.6) передаточное отношение вариатора определится как
■ = 4, d2 d2 d&dn С dtf'
где du d2H dn — средние диаметры ведущего, ведомого и промежуточного фрикционных катков по поверхностям их взаимных контактов.
Диаметрыdx иd2 могут изменяться бесступенчато в зависимости от изменения угла наклона а оси вращения промежуточного катка. При этом с увеличением первого диаметра уменьшается второй и наоборот. Изменением угла а достигается требуемое передаточное отношение.
4.3. Ременные передачи
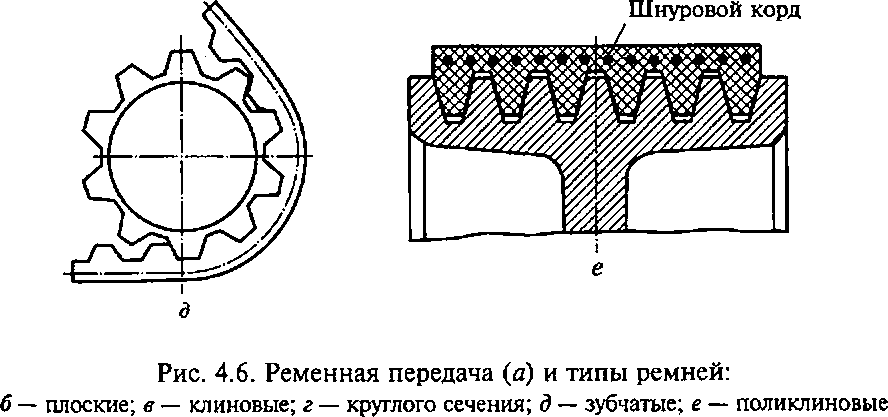
Ременная передача (рис. 4.6, а) состоит из двух закрепленных на валах шкивов и охватывающего их ремня, надетого на шкивы с натяжением. Движение передается за счет сил трения в парах ведущий шкив — ремень и ремень — ведомый шкив.
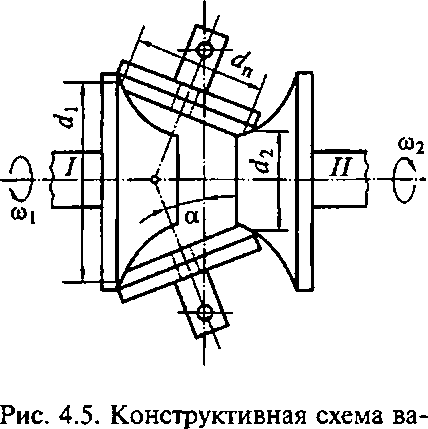
риатора
В состоянии покоя обе ветви ремня натянуты с одинаковыми усилиямиS0. В состоянии передачи движения эти усилия перераспределяются: большим будет усилие S\ в набегающей на ведущий шкив ветви, меньшимS2— в сбегающей с него ветви при
сохранении равенства: +S2= 2 S0. Эти усилия связаны между собой формулой Эйлера
где / — коэффициент трения между шкивом и ремнем; <р — угол обхвата меньшего шкива ремнем.
б
в
г
Данная формула получена в предположении упругого скольжения ремня на всей длине дуги обхвата, обусловленного тем, что при перемещении ремня вместе с ободом в пределах указанной дуги каждый элемент ремня переходит из зоны большего в зону меньшего натяжения, вследствие чего элементы ремня укорачиваются, и ремень несколько отстает от шкива. На ведомом шкиве, наоборот, шкив отстает от ремня. Упругим скольжением обусловлены потери энер-
гии, учитываемые в расчетах силовых параметров КПД, который вместе с потерями в подшипниках, поддерживающих шкивы валов, составляет г| = 0,94...0,96. Кроме того, из-за упругого скольжения происходит дополнительное снижение скорости вращения ведомого шкива, учитываемое коэффициентом £ = 0,97...0,99.
Передаточное отношение ременной передачи
/ = о),/со2 = njn2= D2/{DXQ, (4.10)
гдеD1 иD2 — диаметры ведущего и ведомого шкивов.
Упругое скольжение, при котором шкивы и ремень взаимно проскальзывают на всей длине дуги обхвата, за исключением граничных точек (в начале менее нагруженной ветви на обоих шкивах), не следует смешивать с возникающим при перегрузках передачи буксованием — скольжением ремня по всей дуге обхвата в том числе и в указанных точках.
Полезное окружное усилие определяется разностью усилий: F= = Si
S2. Это усилие связано с вращающими моментами на ведущем (Г,)'и ведомом (Т2) валах соотношениями:
/?=271л/А = 27'2//)2Л2,
из которых и с учетом передаточного отношения (4.10) вытекает прежняя зависимость (4.4) между вращающими моментами Г, и Т2, а также выражение (4.7) для полного КПД передачи.
В ременных передачах применяют следующие типы ремней (см. рис. 4.6): плоские, клиновые, круглого сечения, зубчатые и поликлиновые. Наибольшее распространение в приводах строительных машин получили передачи с плоскими и клиновыми ремнями. Плоские ремни применяют в передачах с передаточным отношением не более / = 4, а клиновые ремни до / = 6...8 и скоростях ремня до 30 м/с. Узкие клиновые ремни допускают работу при скоростях до 40... 50 м/с. В одном комплекте может быть установлено до восьми клиновых ремней. Недостатком многоременных передач является неодинаковая вытяжка ремней в процессе эксплуатации, из-за чего они загружаются неравномерно. Этот фактор учитывают при расчете числа ремней в комплекте с введением специального коэффициента снижения несущей способности ремней от 5... 10 % соответственно при двух—шести и более ремнях. Этого недостатка лишены поликлиновые ремни с высокопрочным полиэфирным кордом, которыми заменяют несколько клиновых ремней, комплектно устанавливаемых на шкивах. Поликлиновые ремни имеют от 2 до 20 ребер. Передаточное отношение передач с поликлиновыми ремнями достигает 15 при скорости 40...50 м/с.
Оптимальным межосевым расстоянием плоскоременной передачи считают:
аопт = 2(0, + D2).
Для клиноременных передач оно изменяется в следующем диапазоне:
от amin = 0,5 (А + Dj) +h доamax = Z>, +D2>
гдеh — высота ремня.
Круглоременные передачи применяют в слабо нагруженных приводах, в частности, в механизмах приборов. Зубчатые ремни отличаются от других наличием на их внут- ; ренней поверхности зубьев, обеспечивающих постоянство передаточного отношения без проскальзывания, бесшумность работы, возможность работы в масле. В отличие от передач со всеми другими типами ремней, передающими движение за счет сил трения между ремнем и шкивами, зубчато-ремен- рис.4.7.натажениерем- ные передачи реализуют принцип передачи т роликом
движения зацеплением. По этому признаку
они более близки к цепным передачам. Зубчатые ремни применяют в передачах большой мощности (до 400 кВт) при скорости до 80 м/с.
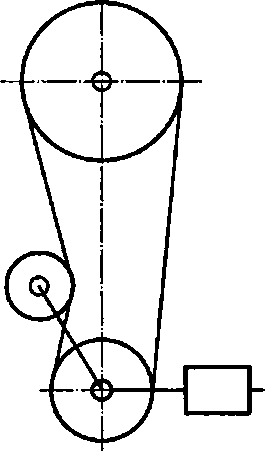
Обязательным условием функционирования ременной передачи является ее натяжение путем перемещения одного из шкивов натяжным роликом (рис. 4.7) или пружиной, автоматическим устройством, регулирующим натяжение в зависимости от внешней нагрузки и т. п. По сравнению с плоскоременными клиноремен- ные передачи требуют меньшего натяжения ремней благодаря тому, что за счет расклинивающего эффекта они имеют более высокий приведенный коэффициент трения fnp (4.9). При стандартном угле клина поперечного сечения ремня а = 40° отношение fnp/f - 2,92. Для обеспечения передачи движения с одинаковыми значениями полезного окружного усилия ^при прочих равных параметрах кли- ноременные передачи требуют натяжения в 1,6—2,2 раза меньше чем плоскоременные передачи.
Достоинствами ременных передач являются: простота конструкции, возможность передачи движения на большие расстояния, способность предохранять механизмы от перегрузок за счет проскальзывания ремня по шкивам. К их недостаткам относятся большие габаритные размеры, недостаточная долговечность ремней, частичная или полная неспособность работать при попадании на ремень и шкивы смазки.
4.4. Зубчатые передачи
Зубчатая передача состоит из двух посаженных на валы зубчатых колес, меньшее из которых называют шестерней, а большее — колесом. Для передачи вращательного движения между двумя валами

F F,
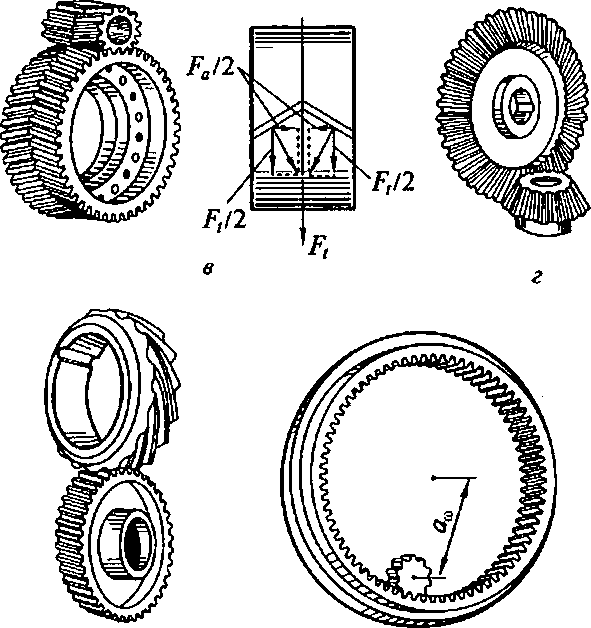
Рис. 4.8. Виды зубчатых передач:
а, б, в — цилиндрические колеса с прямыми, косыми и шевронными зубъями соответственно; г, д — конические колеса с прямыми и круговыми зубъями; е — винтовые колеса; ж — передача внутреннего зацепления; з — зубчато-реечная передача
с параллельными осями применяют цилиндрические колеса с прямыми (рис. 4.8, а иж), косыми (рис. 4.8, б) и шевронными (рис. 4.8, в) зубьями; между валами с пересекающимися осями — конические колеса с прямыми (рис. 4.8, г) или круговыми (рис. 4.8, д) зубьями; между валами с неперекрещивающимися осями — винтовыми колесами (рис. 4.8, е). Для преобразования вращательного движения в поступательное и наоборот служит зубчато-реечная передача (рис. 4.8, з). Передача, в которой зубья колеса находятся на его внутренней поверхности (рис. 4.8, ж), называется передачей внутреннего зацепления.
Зубчатые передачи получили наибольшее распространение в приводах строительных машин благодаря малым габаритным размерам по сравнению с другими механическими передачами, высокому КПД Сп = 0,97...0,99), большой долговечности и надежности, постоянству передаточного отношения, обусловленному отсутствием проскальзывания между сопрягаемыми кинематическими парами, возможности применения в широком диапазоне моментов, скоростей и передаточных отношений. К их недостаткам относится шум при работе на значительных скоростях и в случае недостаточно качественного исполнения. Наиболее часто этот недостаток проявляется в передачах с прямозубыми колесами. Передачи с косозубыми колесами (см. рис. 4.8, б) работают более плавно и менее шумно благодаря большему числу одновременно зацепляющихся пар зубьев. Обычно их применяют при окружных скоростях более 2 м/с. Недостатком этих передач является передача осевых нагрузок на валы, требующая установки их на подшипники, способные воспринимать эти нагрузки. Этого недостатка лишены передачи с шевронными колесами (см. рис. 4.8, в), представляющими собой два зеркально ориентированных косозубых колеса в одной детали. Осевые нагрузки каждой половины такого колеса взаимно уравновешиваются без их передачи на валы. Недостатком шевронных колес является более сложная технология их изготовления.
Зубчатые передачи преобразуют скорости и моменты подобно фрикционным передачам, но без упругого скольжения. Условные окружности зубчатой передачи с цилиндрическими колесами, которые бы имели рабочие поверхности цилиндрических катков эквивалентной в указанном выше смысле фрикционной передачи с такими же передаточным отношением и межосевым расстоянием, называют начальными окружностями. Подобным образом, условные конические поверхности зубчатой конической передачи, по которым обкатываются два конических зубчатых колеса без скольжения, называют начальными конусами. При диаметрах начальных окружностей шестерни и колеса d0] иd$2межосевое расстояние цилиндрической зубчатой передачи определится как аы = (dQi+ d^)/2.
Для конической передачи таким обобщенным параметром служит внешнее конусное расстояние, которое в случае взаимно перпендикулярных ведущего и ведомого валов (рис. 4.9) определяют как
Re= l/2yjdel2+de2,
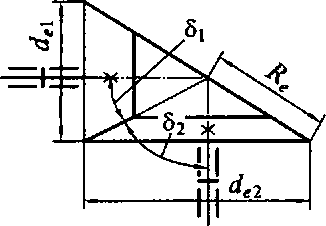
Рис. 4.9. Схема к определению внешнего конусного расстояния для конической зубчатой передачи с перпендику-
гдеdel иde2 — диаметры оснований начальных конусов соответственно шестерни и колеса. лярными валами
Рис. 4.10. Схема эвольвентного зацепления цилиндрических зубчатых колес
В настоящее время наиболее широкое распространение получили зубчатые передачи эвольвентного зацепления, у которых рабочие поверхности зубьев описываются эвольвентой окружности. Эти поверхности имеют цилиндрическую форму у прямозубых цилиндрических колес и коническую у прямозубых конических. Для всех других колес они имеют более сложную геометрическую форму.
Схема эвольвентного цилиндрического зубчатого зацепления представлена на рис. 4.10. Окружность, по которой размечают расстановку зубьев, называют делительной. Часть дуги делительной окружности р между одноименными точками одноименных (правых или левых) рабочих поверхностей зубьев называют окружным шагом зубьев. Эта величина связана с диаметрами делительных окружностей шестерниd\ и колесаd2 и числами зубьев соответственно Z| иz2 соотношениями:
т = р/п = di/z]= d2/z2.
Величину т — часть диаметра делительной окружности зубчатого колеса, приходящуюся на один зуб, называют модулем зубчатого зацепления. Его значения стандартизованы. Шаг и модуль зубьев одинаковы для обоих колес. Модуль и число зубьев являются важнейшими параметрами зубчатого зацепления, по которым, согласно формулам (4.11), определяют диаметры делительных окружностей:
d\ = mzx; d2 = mz2. (4.12)
Число зубьев меньшего колеса (шестерни) ограничено нижним пределом = 17. При меньших значенияхz} толщина зуба у его основания оказывается меньше чем на других уровнях, в связи с чем снижается его изгибная прочность.
Окружность, описанную по головкам зубьев колеса, называют окружностью выступов, а описанную по впадинам зубьев — окружностью впадин. Окружность, по которой обкатывались бы катки цилиндрической фрикционной передачи, эквивалентной зубчатой передаче, называют начальной окружностью. Обычно начальные и делительные окружности совпадают (кроме колес, изготовленных с так называемым смещением исходного контура). В этом случае межосевое расстояние (расстояние между осями зацепляющихся колес) определяют
аш = (di + dJ/2 = m{zi + z2)/2.
Общую точку Р касания начальных окружностей зацепляющихся колес называют полюсом зацепления, а нормаль к боковым поверхностям зубьев в полюсе Р — линией зацепления. Последняя является касательной к основным окружностям. Зацепление колес происходит на линии зацепления на отрезкеKL между точками ее касания к основным окружностям. Общая касательная к делительным окружностям 7Т и линия зацепленияKL образуют угол зацепления а, значение которого для стандартных эвольвентных колес равно 20°.
У косозубых колес зубья наклонены по отношению к оси колеса под углом р (рис. 4.11), составляющем 8... 15°. Чем больше этот угол, тем более плавно работает передача, однако при этом увеличивается также осевая составляющая D„„ , ,,
г. _ _ Рис. 4.11. Схема размеров
(4.11)
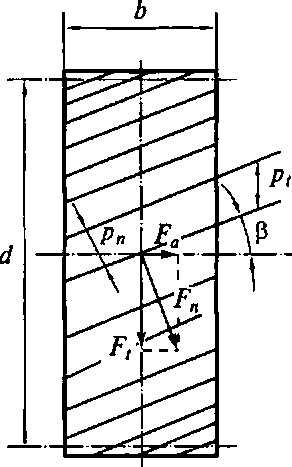
Fa передаваемого зубьями усилия Fn. косозубого колеса
Для шевронных колес, у которых осевые составляющие компенсируются без передачи на валы, обычно принимают р = 25...35°, реже — до 45°. У косозубых (и шевронных) колес различают окружной р, и нормальный шаг р„. Первый измеряют по дуге делительной окружности в сечении, перпендикулярном оси колеса, а второй — по дуге делительного цилиндра в направлении, перпендикулярном рабочим поверхностям зубьев. Различают также соответствующие этим шагам окружной т, и нормальный т„ модули. Окружные и нормальные шаг и модуль связаны между собой соотношениями:
Pi = Рп/COS Р; «I = /"„/COS р.
Обычно стандартным является нормальный модуль. Диаметр делительной окружности косозубого колеса связан с указанными выше категориями модулей зубьев зависимостями:d= m,z = /h„z/cosp.
а = т.
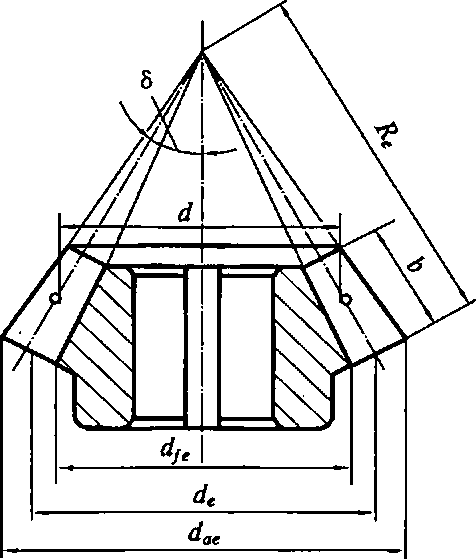
Рис. 4.12. Схема размеров конического зубчатого колеса
Межосевое расстояние косозубой передачи
Z| + z2 _ т„ Z[ + z2 2 cos p 2
У конических зубчатых колес (рис. 4.12) диаметр делительного конуса, а вместе с ними шаг и модуль изменяются по ширине венца. Поэтому у этих колес различают два модуля: средний окружной т на среднем делительном диаметреd и внешний окружной те на внешнем диаметреde. Обычно стандартизован внешний
модуль, с помощью которого определяют все размеры зубчатого колеса, в частности — внешний диаметр делительного конусаde = те z.
Передаточное число и зубчатой передачи с любым видом зубчатых колес (это понятие в зубчатых передачах отождествляют с передаточным отношением) определяют отношением чисел зубьев колеса z2 и шестерни z,: m=z2/z1. Для конической зубчатой передачи при взаимно перпендикулярных осях вращения колес передаточное число, кроме того, может быть определено через половины углов при вершинах делительных конусов б, и82 (см. рис. 4.9): и = ctg б] =tg 52.
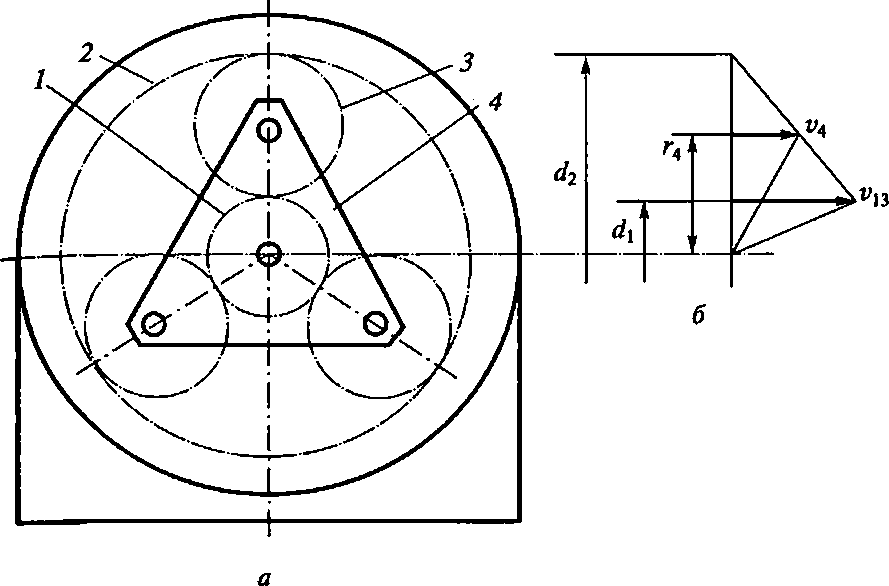
Рис. 4.13. Схема планетарной зубчатой передачи (а) и план скоростей (б)
В последнее время все большее применение в приводах строительных машин находят соосные многопоточные планетарные зубчатые передачи (рис. 4.13, а). Передача состоит из двух центральных колес 1 и 2 и нескольких (обычно трех) сателлитов 3, свободно посаженных на оси водила 4. Ведущими или ведомыми звеньями в этой передаче могут служить водило и любое из центральных колес. Чаще в качестве ведущего используется центральное колесо 1, называемое солнечным, а ведомого — либо водило, либо внешнее центральное колесо 2.
Передаточное отношение определяют по плану скоростей, пример которого представлен на рис. 4.13, б. При ведущем солнечном колесе, вращающемся с угловой скоростью coh его линейная скорость на начальной окружности составитvl3 = со, • d,/2. С такой же линейной скоростью будет перемещаться точка сателлита 3, совпадающая в данный момент с полюсом зацепления колес 1 и 3. Скорость же диаметрально противоположной ей точки того же сателлита, совпадающей с полюсом зацепления колес 2 и 3, при неподвижном внешнем центральном колесе будет равна нулю (i^3 = 0). Линейная скорость центра сателлита составит i>4 = (и13 + г^3)/2 = i>13/2, а угловая скорость вращения водила оа4 = г>4/г4 =vl3/(2r4) = (£>jdi/(4r4), где г4 — радиус осей сателлитов относительно центра вращения водила. Передаточное число определится как: и = щ/ы^ = 4rjdx. Имея в виду, чтоdx- mzx и r4 =(dx+d3)/2 = m(zx+ z3)/2, получим
и = 2 m(zx +z^)/mzx = 2(1 +z3/zx).
Распределение нагрузки с центральных колес на несколько потоков с помощью сателлитов увеличивает соответственно число находящихся в зацеплении зубьев, а их соосное расположение позволяет создавать более компактные и легкие зубчатые передачи с большими передаточными отношениями. Они хорошо встраиваются, например, в барабаны лебедок, в ведущие звездочки гусеничных движителей и других исполнительных механизмов, что в целом уменьшает габаритные размеры и массу машин.
4.5. Червячные передачи
Червячные передачи служат для передачи вращательного движения между перекрещивающимися валами, чаще под прямым углом. Передача состоит из винта 1 (рис. 4.14), называемого червяком, и червячного колеса 2 с зубьями на своем ободе. Ведущим звеном в передаче является обычно червяк.
В сечении в плоскости вращения червячного колеса и проходящего через ось вращения червяка червячная передача подобна зубчато-реечной передаче (см. рис. 4.8, з). Червяк (рис. 4.15, а) представляет собой винт с трапецеидальным профилем витков. Стандартный угол профиля в осевом сечении составляет а = 20°. Осевой шаг нарезки р = кт измеряют по образующей делительного цилиндра диаметром
d\ = mq,
где т — расчетный модуль;q— коэффициент диаметра червяка, значения которого стандартизованы.
1
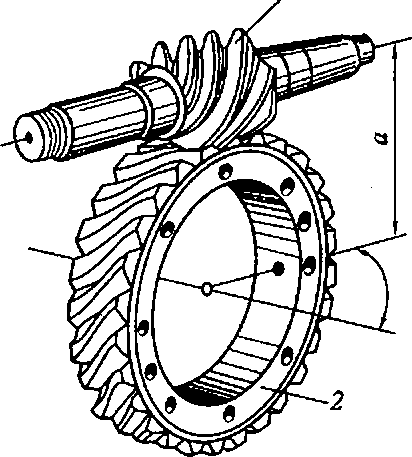
Рис. 4.14. Червячная передача
90° вследствие большего числа зубьев червячного колеса, одновременно находящихся в зацеплении. Однако они более сложны в изготовлении, монтаже и регулировке, особенно после некоторого износа зубьев колеса.
Кроме червяков с цилиндрической делительной поверхностью применяют также гло- боидные червяки (рис. 4.15, б) с торовой делительной поверхностью, охватывающей часть зубьев червячного колеса. Передачи с глобоидными червяками обладают более высокой по сравнению с обычными чер
а
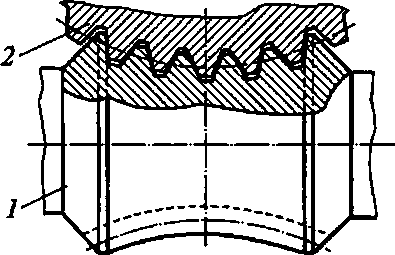
Рис. 4.15. Червяк с цилиндрической (а) и торовой (б) делительными поверхностями
б
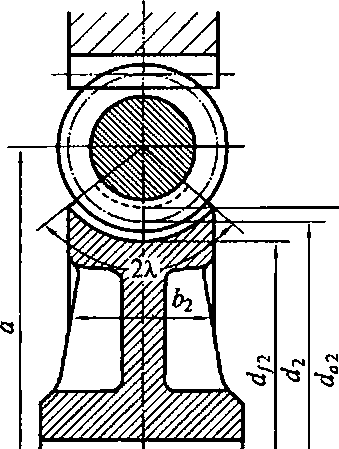
Ради увеличения контактных поверхностей в паре червяк — колесо и снижения за счет этого контактных давлений зубья колеса выполняют охватывающими червяк в его поперечном сечении (рис. 4.16) с центральным углом дуги охвата 2X. = 90... 110°. Для несиловых передач, например, в приводах приборов, червячное колесо может быть выполнено также с цилиндрическим ободом (верхняя часть рис. 4.16).
Диаметр делительной окружности червячного колеса определяют по второй из формул (4.12) для цилиндрических зубчатых колес, а межосевое расстояние в случае совпадения диаметров начальных и делительных поверхностей как
di+d2 q + z2
а = ' „ 1 = т-
2 2
За один оборот червяк смещает колесо на один шаг, соответствующий длине дуги делительной окружности колеса с центральным углом2k/z2. Для одного оборота колеса(2л радиан) червяк должен сделать z2 оборотов. Из этого следует, что передаточное
3 Волков 55
Зуб колеса
Виток червяка
ft
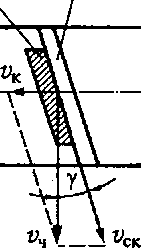
Рис. 4.16. Сечение червячной Рис. 4.17. Схема к объяснению угла передачи плоскостью, перпен- подъема винтовой линии и соотноше-ния скоростей в червячной паречисдо червячной передачи численно равно числу зубьев червячного колеса и = z 2. Этот вывод справедлив только в отношении рассмотренной выше червячной передачи с однозаходным червяком. В дальнейшем передаточному числу червячной передачи будет дано более полное определение. Важным параметром червячной передачи является угол подъема винтовой линии на делительном цилиндре червяка (рис. 4.17), тангенс которого равен отношению шага р к длине делительной окружности: tgy = p/(nd{) = nm/(nmq) = 1 Jq. От угла у зависит отношение окружных скоростей колесаvK и червяка v4, а также скорость скольжения в червячной паре vCK. Скольжение витков червячной нарезки по зубьям червячного колеса является причиной повышенного трения в зоне контактных поверхностей и связанных с этим низкого КПД червячных передач и повышенного износа сопрягаемых элементов трущихся пар. Коэффициент трения зависит от скорости скольжения, уменьшаясь с ее возрастанием. дикулярной оси червяка
Если шаг нарезки червяка увеличить вдвое, не изменяя размеров поперечного сечения витков, и в образовавшееся между двумя смежными витками пространство ввести новую нитку нарезки, то получим двухзаходный червяк. При трехкратном увеличении шага и добавлении двух новых ниток нарезки, образуется трехзаходный червяк и т.д. Число заходов z, определяют по началам или окончаниям витков на одном из торцев червяка. Червяки с одним заходом называют однозаходными, а все остальные — многозаходньши. Оче видно, что угол подъема винтовой линии для z,-заход ного червяка определится из соотношения tg у = pzj(nd{) = zjq. С увеличением числа заходов увеличивается также угол у, вследствие чего при неизменной окружной скорости червяка v4 пропорционально числу заходов Zj возрастает окружная скорость колеса vK и скорость скольжения i> CK. За один оборот z,-заход ный червяк смещает червячное колесо на pz\ или угол 2 tiz(/ z2, а для одного полного оборота колеса по- гтребуется z 2/z t оборотов червяка. Другими словами, за каждый оборот червяка червячное колесо поворачивается на Z] зубьев. Из этого следует, что передаточное число и = СО,/Ш 2 = щ/п2 = Z 2/Z|. Эта формула является общей для определения передаточного числа червячной передачи, а приведенное ранее соотношение и = = z 2 есть ее частный случай при zx = 1. Из второго вывода о пропорциональном изменении скорости скольжения vCK тангенсу угла подъема винтовой линии у следует, что при увеличении числа заходов червяка уменьшаются потери энергии на трение в сопрягаемой кинематической паре. С учетом потерь в подшипниках червяка и вала червячного колеса общий КПД червячной передачи при zx = I, 2 и 3 при работе в масляной ванне составит соответственно 0,7...0,75; 0,75...0,82 и 0,82...0,92. Для открытой одно- и двухзаходной червячной передачи ri = 0,6...0,7, для самотормозящейся передачи г] = 0,4...0,45. Ведущим органом в червячной передаче обычно является червяк. Обратимость движения — от червячного колеса к червяку — возможна только при условии, когда угол подъема винтовой линии у оказывается больше угла трения в сопрягаемой кинематической паре. Обычно этим свойством обладают передачи с многозаходны- ми (трех-, иногда двухзаходными) червяками. Передачи, не обладающие этим свойством (обычно с однозаходными червяками), называют самотормозящимися, что означает невозможность самопроизвольного раскручивания червяка (ведущего звена передачи) внешними нагрузками, приложенными к валу червячного колеса. Достоинствами червячных передач, способствующими их широкому распространению в приводах строительных машин, являются: бесшумность работы, возможность получения больших передаточных отношений при малых габаритных размерах передачи, высокая точность перемещений, возможность обеспечения самоторможения. К их недостаткам относятся: сравнительно низкий КПД, небольшие передаваемые мощности (до 70 кВт), повышенный износ витков червяка и зубьев колеса, необходимость применения дорогостоящих материалов (бронзовые венцы червячных колес) для уменьшения коэффициента трения контактирующих Поверхностей.
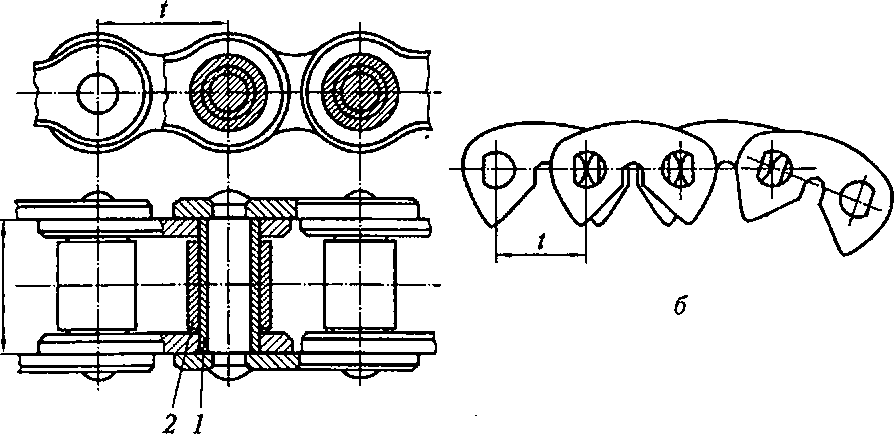
Рис. 4.19. Втулочно-роликовая (а) и зубчатая (б) приводные цепи
а4.6. Цепные передачи Цепные передачи служат для передачи вращательного движения между двумя параллельными валами при значительном расстоянии межцу ними. Передача (рис. 4.18) состоит из двух звездочек 1 и 3 и охватывающей их цепи 2. В строительных машинах в качестве приводных цепей чаще применяют втулочно-роликовые (рис. 4.19, а), реже зубчатые (рис. 4.19, б) цепи. Оба вида цепей могут быть однорядными и многорядными, для передачи движения несколькими параллельными потоками. Втулочно-роликовые цепи применяют при скоростях до 20 м/с, а зубчатые — до 25 м/с. Последние работают с меньшей вибрацией и шумом, в связи с чем их называют бесшумными. Основными параметрами приводных цепей являются: шаг t и разрушающая нагрузка. 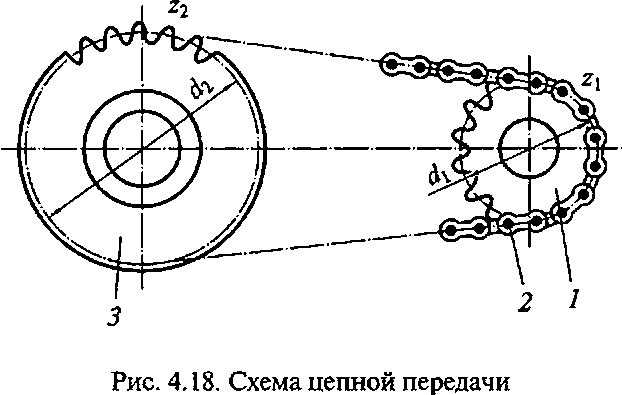
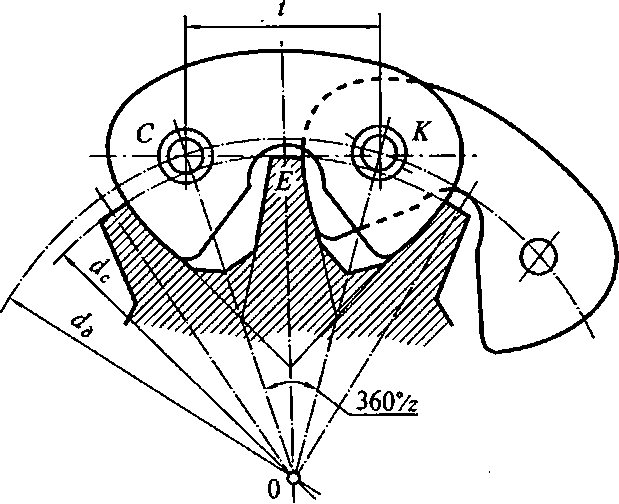
Рис. 4.20. Форма зубьев звездочек для ролико-втулочных (а) и зубчатых (б)
цепей
бФорма зубьев звездочек (рис. 4.20) зависит от типа и размеров цепи. Минимальное число зубьев звездочек ограничено в связи с износом шарниров, неравномерностью скорости и шумом при работе. Для передач с втулочно-роликовыми цепями его назначают от 12 (при передаточных числах и > 6) до 31 (при и = 1), для передач с зубчатыми цепями — от 16 до 40 при тех же передаточных числах. ■ Диаметр делительной окружности звездочки dd связан с числом ее зубьев z и шагом цепи t зависимостью: dd= t/sin(n/z). Межосевое расстояние находится в следующих пределах, мм: a min = 0,6(4,, + + da2) + 30... 50; On,ах = 80/ при оптимальном значении аот = (30... 50 )t, 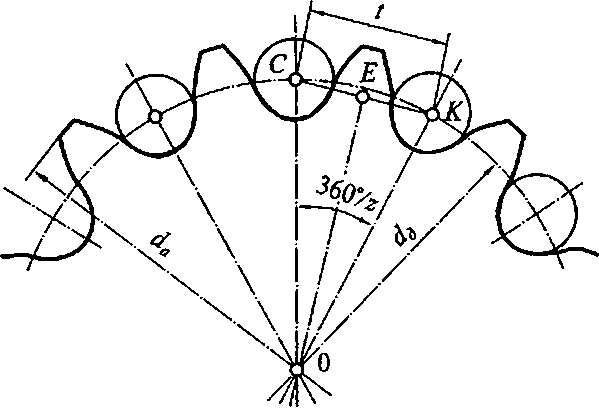 меньшие значения — для малых передаточных чисел (« = 1... 2), большие — для и = 6...7. При вращении ведущей звездочки с постоянной угловой скоростью СО] линейная скорость движения цепи v не остается постоянной из-за переменного радиуса шарнира, сбегающего со звездочки звена цепи или набегающего на нее. При взаимодействии цепи с ведомой звездочкой на эту неравномерность накладывается новая пульсация, вследствие чего угловая скорость ведущей звездочки о) 2, а вместе с ней и передаточное число и = со,/сй 2не остаются постоянными. В расчетах цепных передач определяют среднее передаточное число и = z2lz\-По сравнению с ременными передачами, в составе которых также имеется гибкая связь, цепные передачи более компактны, их валы оказываются менее нагруженными вследствие незначительного натяжения приводных цепей, имеют сравнительно высокий КПД (т| = 0,96...0,98). К их недостаткам относятся: вытягивание цепей вследствие износа шарниров, чувствительность к перекосам валов, непостоянство передаточного отношения, особенно при малых числах зубьев звездочек. Цепные передачи широко применяют в приводах машин мощностью до 100 кВт. При больших передаваемых мощностях резко возрастает стоимость передачи. 4.7. Валы и осиВращающиеся элементы передач устанавливают на валах и осях. Вал (рис. 4.21), являясь для посаженной на него детали (зубчатого колеса, звездочки, шкива и т.п.) поддерживающим звеном, в то же время передает крутящий момент либо от силовой установки ведущему звену первой передачи трансмиссии, либо от ведомого звена последней передачи трансмиссии исполнительному механизму или рабочему органу. Во всех случаях вал вращается вместе с поддерживаемыми им звеньями, для чего его соединяют с этими звеньями посредством шпонок — призматических, клиновых или сегментных стержней и пластин, закладываемых в продольные пазы вала и ступицы — центральной части соединяемой с валом детали, или шлицевых соединений — равномерно расположенных по окружности цилиндрической поверхности вала и ступицы пазов и выступов. По несущей способности шпоночное соединение уступает шлицевому. Его применяют в малонагруженных мелкосерийных изделиях. Шпоночное или шлицевое соединение может быть неподвижным — без возможности осевого перемещения соединяемых деталей относительно друг друга и подвижным — с возможностью такого перемещения. Вращающееся звено передачи может быть выполнено вместе с валом как единая деталь. Различают прямые, коленчатые и гибкие валы. В трансмиссиях строительных машин применяют преимущественно прямые валы. вРис. 4.21. Валы: а — прямые; б — коленчатые; в — гибкиеКоленчатые валы применяют, в частности, в коленчато-рычаж- ных механизмах, например в двигателях внутреннего сгорания. Гибкие валы служат для передачи вращающего момента между узлами машин и агрегатами, меняющими свое взаимное положение при работе, например, в механизированном ручном инструменте, вибраторах, приборах дистанционного управления и контроля и т.п. Гибкий вал состоит из сердечника и нескольких плотно навитых на него слоев проволок с противоположной навивкой смежных слоев. Для защиты от повреждений, загрязнений и сохранения на валу смазки, а также защиты обслуживающего персонала от захвата вращающимся валом, его заключают в невраща- ющуюся металлическую, резиновую или тканевую броню. |
 Скачать 5.2 Mb.
Скачать 5.2 Mb.