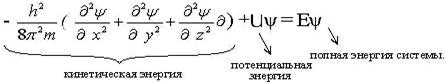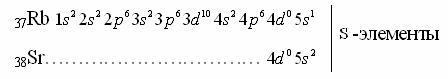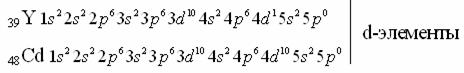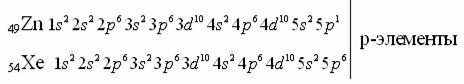|
|
ХИИИИИИИИМИИИИЯЯЯЯЯ. Тема 1 химия как наука и её значение в жизни человека
Тема 4: СТРОЕНИЕ ЭЛЕКТРОННОЙ ОБОЛОЧКИ АТОМОВ
1.Строение атома водорода по Н. Бору.Постулаты Н. Бора.
2.Линейчатость спектра атома водорода.
3.Основные положения квантовой механики.Волновая природа электрона.Понятие об орбиталях.
4.Квантово-механическая модель атома: а) квантовые числа; б) электронные конфигурации атомов и ионов.
5.Главная причина периодичности свойств химических элементов.
Строение атома водорода по Н. Бору. Постулаты Н. Бора.
В 1913 г. Н. Бор предложил теорию строения атома водорода, в которой он связал планетарную модель атома с квантовой теорией излучения М. Планка и учением А. Эйнштейна о световых квантах.
Квантовую теорию излучения предложил в 1900 г. М. Планк (Германия). Он высказал предположение, что вещества поглощают и испускают энергию дискретными порциями, названными им квантами. Энергия кванта Е пропорциональна частоте излучения (колебания) υ:
Е=hυ,
где h – постоянная Планка(6,626•10-34Дж∙с), υ – частота колебаний.
В 1905 г. А. Эйнштейн разработал квантовую теорию света, согласно которой свет – поток световых квантов – фотонов, энергия которых определяется уравнением М. Планка. Волновые свойства фотона выражаются уравнением: с= λ•υ, где λ – длина волны,
отсюда и энергия фотона равна
Е=. (І)
Но фотон с энергией Еобладает и некоторой массой «m», поэтому в соответствии с уравнением А. Эйнштейна энергия равна:
Е= mс2. (ІІ)
Объединяя эти два уравнения имеем:
; .
Это уравнение описывает волновые (λ) и корпускулярные (m) свойства фотона, т.е. фотону присущая корпускулярно-волновая двойственность.
Основываясь на положении квантовой теории света о прерывистой, дискретной природе излучения, Н.Бор сделал вывод, что энергия электронов в атоме тоже должна меняться скачкообразно, т.е. дискретно. Поэтому в атоме возможны не любые энергетические состояния электронов, а лишь определенные «разрешенные» состояния, т.е. энергетические состояния электронов в атоме квантованы. Переход из одного разрешённого состояния в другое совершается скачкообразно и сопровождается испусканием или поглощением кванта электромагнитного излучения.
Основные положения своей теории Н. Бор сформулировал в виде 3 постулатов:
1. Электрон вращается вокруг ядра не по любым, а некоторым определенным круговым орбитам. Эти орбиты получили название стационарных.
2. Двигаясь по стационарной орбите, электрон не излучает и не пог-лощает энергию. Находясь на стационарной орбите, электрон находится в основном состоянии, а на более высоких орбитах – в возбужденном. В основном состоянии энергия связи электрона с ядром максимальна, а энергия атома – минимальна.
3. Излучение происходит при скачкообразном переходе электрона с одной стационарной орбиты на другую. При этом испускается или поглощается квант электромагнитного излучения, энергия которого равна разности энергии атома в конечном и исходном состояниях.
Это положение требует некоторых пояснений.
Наименьшей энергией электрон обладает, находясь на ближайшей к ядру орбите (нормальное состояние). Для того чтобы перевести электрон на более удаленную от ядра орбиту, нужно преодолеть притяжение элект-рона к положительно заряженному ядру, что требует затраты энергии. Этот процесс сопровождается поглощением кванта света. Соответственно, энергия атома при таком переходе увеличивается, а электрон находится в возбужденном состоянии (в возбужденном состоянии электрон может находиться сек.).
Переход электрона в обратном направлении, т.е. с более удаленной орбиты на более близкую к ядру, приведет к уменьшению энергии атома, а освободившаяся энергия будет выделена в виде кванта электромагнитного излучения. Отсюда рассчитывается разность энергии атомов в начальном и конечном состоянии:
∆Е =Ен – Ек.
где Ен - энергия атома при нахождении электрона на более удаленной от ядра орбите. Ек – энергия атома при нахождении электрона на более близкой от ядра орбите.
Из уравнения Планка Е =hυ получим :
∆Е =hυ; υ=; λ=
Последнее уравнение позволяет вычислить возможные частоты(υ) или длины волн (λ) излучения, способного испускаться или поглощаться атомом, т.е. рассчитать спектр атома. Как видно из формулы λ= длина волны (λ) зависит от величины излучаемой энергии.
Н. Бор объяснил происхождение оптического спектра водорода. Линейчатость спектра он объяснил переходом электрона на нижележащие уровни с возбужденного состояния. Он вычислил положение спектральных линий в видимой части спектра и предсказал существование спектральных линий (неизвестных в то время), находящихся в ультрафиалетовой (УФ) и инфракрасной области спектра. Впоследствии эти серии линий были экспериментально обнаружены в соответствии с расчетами Н. Бора.
в начало
Линейчатость спектра атома водорода.
В настоящее время спектр атома водорода имеет следующие серии линий:
1. Если электрон переходит с возбужденного состояния на І-ый энергетический уровень (стационарную орбиту) возникает серия линий Лаймана, лежащая в УФ области спектра (Е большая, а λ малая).
2. При переходе электрона с возбуждённого состояния на ІІ-ой уровень появляется серия линий Бальмера, лежащая в видимой части спектра (Е уменьшается, а λ увеличивается).
3. При возвращении электрона с возбужденного состояния на ІІІ-ий уровень в спектре появляется серия линий Пашена, лежащая в инфракрасной области спектра (Е – уменьшается, λ – увеличивается).
4. При переходе электрона с возбужденного состояния на 4, 5, 6 уровни появляются в спектре серии линий, лежащие в далекой инфракрасной области.
Однако теория страдала противоречивостью, которую сознавал сам Бор:
1. Теория постулировала положения, противоречащие классической механике.
2. Теория не объясняла, где находится электрон при переходе с одного на другой энергетический уровень (промежуточное состояние между исходной и конечной орбитой «запрещается» теорией, поскольку постулируется возможность пребывания электрона только на стационарных орбитах).
3. Теория не дает объяснение более тонкому строению атома.
Со временем теория Бора была усовершенствована: А. Зоммерфельд считал, что движение электрона в атоме возможно не только по круговым, но и по эллиптическим орбитам.
Все же теория Бора была важным этапом в развитие представлений о строении атома. Она показала, что нельзя автоматически переносить законы природы, справедливые для больших тел – объектов макромира, на ничтожно малые объекты микромира – атомы, электроны, фотоны. Поэтому и возникла задача разработки новой физической теории пригодной для описания свойств и поведения объектов микромира. Эта задача была решена в 20-х годах XX века, после возникновения и развития новой отрасли теоретической физики – квантовой или волновой механики.
Основу квантовой механики заложили работы: М. Планка, Н. Бора, А. Эйнштейна, В. Гейзенберга, Э. Шредингера.
в начало
Основные положения квантовой механики
Квантовая механика основывается на представлениях о квантовании энергии, волновом характере движения микрочастиц, вероятностном методе описания микрообъектов.
Создание квантовой механики произошло на пути обобщения представления о корпускулярно – волновой двойственности фотона на все объекты микромира и прежде всего на электрон.
В 1924 году Луи де Бройль предположил, что корпускулярно – волновые свойства присущи не только фотонам, но и электронам. Поэтому электрон должен проявлять волновые и корпускулярные свойства и уравнение для характеристики электрона должно иметь вид: λ= (заменив «с» – скорость света, на «υ» – скорость движения электрона). Уравнение Луи де Бройля – основное уравнение квантовой механики. Рассчитаем λ для электрона:
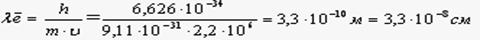 (1) (1)
И для сравнения рассчитаем λ для макрочастицы с m=1, =5м/сек.
λ= (2)
Если размеры атома , то λ для всех макротел значительно меньше, чем размер атома. Волны частиц материи де Бройль назвал материальными волнами. Они свойственны всем частицам или телам. Однако, как следует из расчета (2) для макротел длина волны настолько мала, что в настоящее время не может быть обнаружена. А у электронов длина волны соизмерима с размером атома и они проявляют волновые свойства.
Через 3-4 года после появления уравнения Луи де Бройля, описывающего двойственную природу электрона, были получены экспериментальные данные, подтверждающие дуализм электрона. Так в 1927г. К. Девиссон и Л. Джермер в США, Д. Томсон в Англии и П. Тартаковский в России независимо друг от друга установили дифракцию электрона при прохождении пучка электронов через кристаллическую решетку некоторых соединений. Затем была открыта интерференция.
Новое двойственное корпускулярно-волновое представление об электроне заставило пересмотреть принятую прежде модель атома, согласно которой электрон в атоме движется по определённым круговым или эллиптическими орбитами.
Волновая механика доказывает, что в отношении микрочастиц нельзя с достаточной точностью одновременно определить как положение частицы в пространстве (т.е. ее координаты), так и скорость движения частицы. Следовательно, теряется и возможность представить и траекторию её пути. Это важное заключение известно под названием принцип неопределенности В. Гейзенберга (1927): невозможно одновременно определить и скорость частицы (импульс) и ее положение (координаты) ∆р∙∆q (р – импульс, q – координаты) Данное соотношение показывает, что чем точнее определяется координата частицы, тем более неопределенным становится её импульс, и наоборот
∆р=m•υ
где m – масса, υ – скорость)
Согласно этому принципу, понятие об электронных орбитах в атоме теряет свой физический смысл: речь идёт лишь о вероятности появления движущего электрона в данный момент времени в данной точке внутриатомного пространства. Положение же электрона в последующий момент может быть определено со сравнительно небольшой степенью вероятности. В связи с этим в квантовой механике состояние микрочастицы полностью описывается не её координатой и скоростью, а некоторой волновой функцией ψ (пси), определяющей вероятность нахождения электрона в определённой области пространства. Волновая функция, подобно амплитуде любого волнового процесса, может принимать как положительное так и отрицательное значение. Математически это записывается так:
ψ = ψ * (x, y, z),
где x,y,z – координаты.
Применяют ψ2, которая всегда положительна. Она характеризует плотность вероятности нахождения электрона в соответствующей областиоколоядерного пространства. Отсюда появилось понятие орбиталь: пространство вокруг ядра, в котором наиболее вероятно нахождение электрона.Величина области пространства, которую занимает орбиталь, обычно такова, чтобы вероятность нахождения электрона внутри неё составляла не менее 95%. Так как электрон несет отрицательный заряд, то его орбиталь представляет собой распределение заряда, которое получило название электронного облака (в нем сосредоточена преобладающая часть заряда и массы электрона90%).
Рассчитать вероятность нахождения электрона в данный момент в любой точке трехмерного околоядерного пространства позволяет уравнение Э. Шрёдингера (Австрия, 1927). Применительно к атому водорода уравнение записывается:
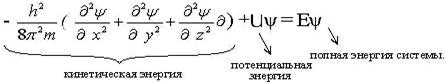
где h – const Планка; m – масса частицы; x,y,z – координаты; ψ – волновая функция.
Наличие 3х степеней свободы (3х координат) приводит к тому, что в решении появляются 3 величины, которые принимают только целостные значения. Эти три параметра называются квантовыми числами: главное (n), орбитальное () и магнитное () – квантовое число. Было показано, что электрон также характеризуется четвертым квантовым числом – спиновым (ms).
в начало
Квантово-механическая модель атома: а) квантовые числа; б) электронные конфигурации атомов и ионов.
Итак, положение каждого электрона в атоме характеризуется четырьмя квантовыми числами.
n– главное квантовое число. Определяет энергию и размеры электронных орбиталей, т.е. чем ближе к ядру находится электрон, тем меньше его энергия. Принимает значение от 1 до ∞, указывает на число энергетических уровней, и равно номеру периода.
l– орбитальное (побочное) квантовое число.
Электронные оболочки расщеплены на подоболочки, поэтому «» характеризует энергетические подуровнив электронной оболочке. Рассчитывается «» как n-1и, принимая целостные значения, указывает на число подуровней на уровне. Различная форма энергетических подуровней обозначаются буквами: s – сферическая форма; р – гантелеобразная форма; d – две скрещенные гантели; f – три скрещенные гантели. Соответственно, от места нахождения электронов, они бывают s,p,d,f электроны.
ml – магнитное квантовое число.
Характеризует ориентацию орбитали в пространстве и принимает значение от – до + , через «0».
Положение электрона в атоме характеризующееся определенными значениями квантовых чисел n, l,ml – называются атомной орбиталью (АО).
Условно АО изображают в виде энергетической ячейки .
Четвертое квантовое число спиновое – m.
Определяет вращение электрона вокруг собственной оси и не связано с движением электрона вокруг ядра. Принимает только два значения 1/2, что соответствует направлению вращения вокруг оси. Спин- величина векторная и его условно обозначают противоположно направленными стрелками  . .
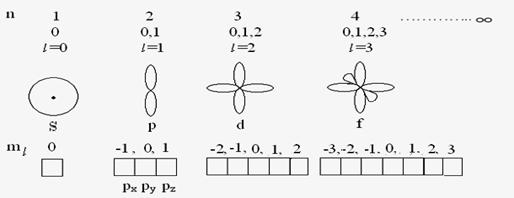
Итак, четыре квантовые числа n, l, , ms полностью характеризуют состояние электрона в атоме.
Многоэлектронные атомы. В этих атомах каждый электрон не только притягивается ядром, но и испытывает отталкивание от всех остальных электронов в соответствии с законом Кулона. Точное решение уравнения Шрёдингера для многоэлектронных атомов неизвестно. Существует ряд приближенных расчетов, исходя из допущения, что волновая функция многоэлектронной системы может быть представлена в виде суммы волновых функций отдельных электронов. Тогда уравнения Шрёдингера может решаться отдельно для каждого находящегося в атоме электрона, состояние которого, как и в атоме водорода, будет определяться значением квантовых чисел n, , , ms. Однако и такое упрощенное решение уравнения Шрёдингера для многоэлектронных атомов и молекул, представляет весьма сложную задачу и в настоящее время выполняется с помощью ЭВМ. В многоэлектронном атоме внутренние электронные уровни экранируют (заслоняют) электроны, расположенные на внешних энергетических уровнях от действия ядерного заряда. При этом для электронов, различающихся значением , экранирование происходит неодинаково. Таким образом, в многоэлектронных атомах энергия электрона зависит не только от главного, но и от орбитального () квантового числа. Главное квантовое число(n) определяет лишь некоторую энергетическую зону, в пределах которой точное значение энергии электрона определяется величиной «».
В 1925 г швейцарский физик Вольфганг Паули сформулировал принцип или запрет Паули: в атоме не может быть двух электронов, имеющих одинаковый набор всех четырех (n,l,,ms) квантовых чисел.
-
Из этого следует, что два электрона в атоме могут занимать одну атомную орбиталь при условии, что их спины антипараллельны
(различное ms).
Пользуясь принципом Паули можно рассчитать максимальное число электронов на различных уровнях и подуровнях в атоме, то есть емкость уровней и подуровней.
Максимальное число электронов на уровне равно 2n2 (n-главное квантовое число), максимальное число электронов на подуровне рассчитывается по формуле 2 (2l +1).
1=0
|
s-2 ē
|
1=1
|
p-6 ē
|
1=2
|
d-10 ē
|
1=3
|
f-14 ē
|
Запись распределения электронов в атоме по оболочкам, подоболочкам и орбиталям получила название электронной конфигурации элемента
В основе заполнения электронной оболочки атома лежат: принцип Паули, принцип наименьшей энергии, правилоХунда и Клечковского.
Принцип минимальной энергии.
Согласно этому принципу электрон в первую очередь располагается в пределах электронной подоболочки с наинизшей энергией.
ПравилоХунда:в наиболее устойчивом состоянии атома электроны размещаются в пределах электронных подуровней (подоболочек) так, чтоб их суммарный спин был максимален.
Это правило определяет порядок размещения электронов в пределах одного подуровня для наиболее устойчивого состояния атома. Например:
Правила В. Клечковского.
Первое правило: электрон обладает наименьшей энергией на той электронной подоболочке, где сумма квантовых чисел n+l минимальна.
Второе правило: электрон обладает наименьшей энергией на подоболочке с наименьшим значением главного квантового числа.
Электронные конфигурации атомов записываются в виде электронных формул, то есть распределения электронов атома по оболочкам иподоболочкам. При записи электронных формул следует указать для атома: номер периода (число оболочек), число подоболочек для каждой оболочки, порядковый номер элемента, а при графическом построении электронных формул электроны располагают в энергетические ячейки.
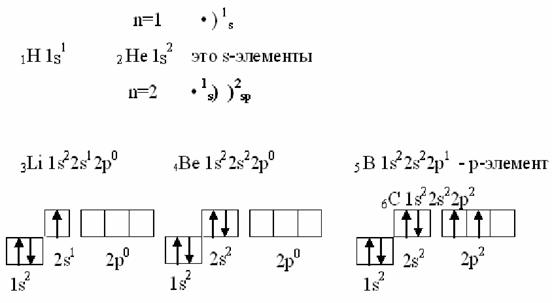
Порядок распределения электронов у атома углерода на 2р2 оболочке представляет собой пример общей закономерности, выраженной правиломХунда: электроны размещаются на оболочке 2р2 так, чтоб их суммарный спин был максимальный (1/2+1/2=1).
Последним элементом второго периода является 10Ne.
Таким образом, во втором периоде: два s-элемента и шесть р-элементов.

Также как и во ІІ периоде, третий период имеет: два s – элемента, шесть – p – элементов. Но период закончился, а 3d подоболочка не заполнена.
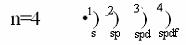
19K 1s22s22p63s23p63d04s1 s-элемент.
Чтобы решить вопрос какой уровень 3d или 4s будет заполняться, нужно рассчитать сумму n+.
l=0
|
4s
|
n+l=4+0=4
|
l=2
|
3d
|
n+l=3+2=5
|
Меньше сумма n+ у 4s уровня (первое правило Клечковского), значит заполняется 4s1 уровень.
20Ca s-элемент
21Sc d-элемент.
При заполнении электронной оболочки атома скандия нужно рассчитать сумму n+l для 3d и 4p уровней:
l=2
|
3d
|
n+l=3+2=5
|
l=1
|
4p
|
n+l=4+1=4
|
Сумма n+l в обоих случаях одинаковая, значит, согласно второму правилу Клечковского заполнение орбиталей происходит по меньшему «n», то есть будет заполняться 3d1.
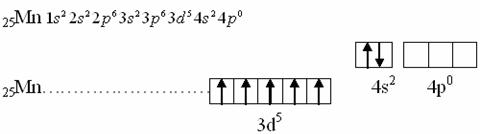
Как видно из этих электронных формул, заполнение 3d происходит не наружного уровня, а нижележащего при заполненном 4s наружного уровня:
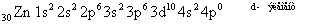
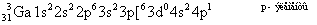
.
Четвертый период закончился, а подоболочки 4d и 4f остались незаполненные. Из вышеперечисленных выводов ясно, что 4d будет заполняться в 5 периоде, а 4f- в 6 периоде.
Итак, 4 период имеет 18 элементов: два – s-элемента, десять – d-элементов, шесть – p-элементов.
n = 5 • ) ) ) ) )
Пятый период- аналог четвертого, то есть тоже имеет 18 элементов: два s-элемента, десять d-элементо12в, шесть p-элементов. Начинается период сs-элементов.
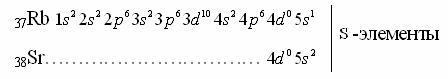
Затем заполняется 4 подоболочки
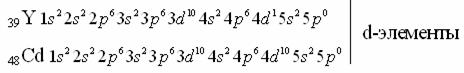
И далее шесть р-элементов
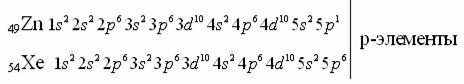
Шестой период имеет 32 элемента. Из незаполненных оболочек предыдущих периодов здесь будет заполняться 4 f и 5 d подоболочки. Располагаяорбитали в порядке увеличения энергии, их заполнение происходит следующим образом:
1s<2s< 2p< 3s< 3p< 4s< 3d< 4p< 5s< 4d< 5p< 6s< 5d1
< 4f1-14< 5d2-10< 6p < 7s< 6d1< 5f1-14< 6d2-10< 7p
Выводы:
1. s-элементы расположены в главных подгруппах (А- подгруппы) 1 – 2 группы;
2. p-элементы расположены в главных подгруппах (А- подгруппы) 3 – 8 группы;
3. d-элементы расположены в побочных подгруппах (В-подгруппы) 1 – 8 групп;
4. f-элементы – лантаноиды и актиноиды.
в начало
Главная причина периодичности свойств химических элементов.
Из изложенного следует, что по мере роста заряда ядра атома происходит закономерная периодическая повторяемость сходных электронных конфигураций, а следовательно и повторяемость свойств элементов: все периоды начинаются s-элементами и заканчиваются p-элементами. Поэтому главной причиной периодичности свойств элементов является периодическое появление однотипных электронных конфигураций внешних электронныхподоболочек с ростом заряда ядра атома элемента. В связи с этим современная формулировка периодического закона гласит:
Cвойства элементов и их соединений находятся в периодической зависимости от заряда ядра атомов и определяются периодически повторяющимися однотипными электронными конфигурациями их атомов.
В порядке заполнения электронных орбиталей имеются отступления – «провал» или «проскок» электронов: электроны с последней подоболочки(s) проваливается на нижележащую подоболочку (d).
«Провалы» электронов наблюдаются для многих элементов. Они оправданы энергетически, то есть подчиняются принципу наименьшей энергии, и находят экспериментальное подтверждение при изучении тонкой структуры спектров.
«Провал» электронов имеется у атомов: Ag, Au, Cu, Mo,Cr, Nb, Ru, Rh, Pd и др. Например, 29Сu , происходит заполнениеподоболочки d полностью, что оказывается энергетически выгодным, а атом меди приобретает устойчивую электронную конфигурацию.
Можно записать электронную формулу не только атома, но и иона, учитывая при этом отданные или принятые электроны атомом.
Например:
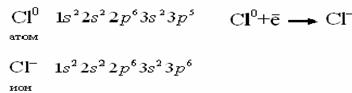
в начало
|
|
|
 Скачать 1.07 Mb.
Скачать 1.07 Mb.