Книга мікроекономіка. Тема предмет і метод мікроекономіки
 Скачать 1.13 Mb. Скачать 1.13 Mb.
|
Залежність виробництва зошитів від збільшення витрат праці(при інших незмінних факторах виробництва)
Рис. 7.1. Кривасукупного продукту змінного фактора  Q Q1 OQ Q q  А      В ВС Х1 Х  співвідношення координат точки А: Q1/Х1 - це середній продукт у цій точці. Середній продукт досягає максимуму при умові використання такої кількості змінного фактора, яка відповідає точці дотику променя, який виходить з початку координат та кривої сукупного продукту. На рис. 7.1 це точка О. Якщо провести дотичні до будь-якої точки кривої сукупного продукту то можна знайти тангенси кутів, що вони утворюють з віссю X. Тангенс будь-якого з цих кутів дорівнює граничному продукту. Середній продукт буде збільшуватися доти, поки граничний продукт буде більший за нього (рис. 7.2.). 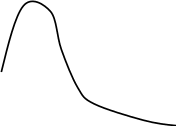  Q Q А  С АР | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Витрати праці (L), тис. люд.-год. | Обсяг виробництва зошитів, тис. шт, при витратах капіталу (К), тис. год. | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 10 | 20 | 30 | 40 | 50 |
| 2 | 20 | 30 | 50 | 75 | 90 |
| 3 | 40 | 50 | 75 | 140 | 180 |
| 4 | 45 | 75 | 140 | 180 | 220 |
| 5 | 50 | 90 | 180 | 225 | 250 |
В
 иробнича сітка показує, що деякі обсяги продукції можна отримати при різних альтернативних наборах факторів виробництва: 50 тисяч зошитів при L=5, К=1 та L=3, К=2 і т. д. Якщо графічно сполучити точки, що характе-ризують альтернативні комбінації факторів при певному обсязі виробництва продукції, то отримаємо криву, що називається ізоквантою (рис. 7.3).
иробнича сітка показує, що деякі обсяги продукції можна отримати при різних альтернативних наборах факторів виробництва: 50 тисяч зошитів при L=5, К=1 та L=3, К=2 і т. д. Якщо графічно сполучити точки, що характе-ризують альтернативні комбінації факторів при певному обсязі виробництва продукції, то отримаємо криву, що називається ізоквантою (рис. 7.3).
 К К
К К

K
 1 5 М R
1 5 М RN
K
 2 1
2 1
 1 3 5
1 3 5L1 L2 L L
Рис. 7.3. Ізокванта Рис. 7.4. Карта ізоквант
Ізокванта - це крива, що відображає альтернативні варіанти ресурсів, що використовуються для виробництва певного обсягу продукції. Точки М і N показують такі комбінації факторів виробництва (L і К), що дають змогу виробити 50 тисяч зошитів. А комбінація К дає змогу виробити їх значно більше. Через цю точку можна провести іншу ізоквоту. Так будується карта ізоквант (рис. 7.4).
Карта ізоквант – це множина ізоквант, що відображає максимальний випуск продукції за будь-яких комбінацій факторів виробництва. Криві ізоквант ніколи не перетинаються. Чим далі ізокванта від початку координат, тим більшому обсягу виробництва продукції вона відповідає.
Аналізуючи ізокванти можна визначити показник заміщення одного фактора виробництва іншим. Гранична норма технологічного заміщення капіталу працею (МRТSKL) визначається обсягом праці, яка може замінити одиницю капіталу:
МRТSKL = L / K = L2-L1 / K2-K1
Гранична норма технологічного заміщення праці капіталом (MRTSLK) визначається обсягом капіталу, який може замінити одиницю праці:
МRТSLK = K / L
Граничну норму технологічного заміщення факторів виробництва можна також розрахувати через граничні продукти.
Дійсно, якщо при зменшенні капіталу з К1 до К2 та зростанні кількості праці з L1 до L2 (див. 7.3), виробник залишається на тій самій ізокванті, то можна довести таку рівність:
K / L = - МРL / МPK
О
 скільки МРL= ТРL /L, а МPK = ТPK / K, то:
скільки МРL= ТРL /L, а МPK = ТPK / K, то:МРL / МPK = ТРL /L ТPK /K= ТРL /L*K /ТPK = - К /L
Оскільки ТРL і ТPK - це зміни сукупного продукту під впливом змін відповідних факторів виробництва (L і К), то на одній ізокванті вони повинні взаємно компенсуватись, щоб загальна кількість продукції не змінилась. Причому зміни сукупного продукту (ТРL і ТPK) різнонаправлені, тобто мають різний знак, адже праця збільшується, а капітал зменшується. Саме через це в доведеній нами рівності з'являється знак “мінус”:
МРL / МPK = - К /L
Цю рівність можна переписати і так:
MRTSLK = К /L = - МРL / МPK
Ф
Це означає, що кожну втрачену одиницю капіталу приходиться заміняти все біль-шою кількістю праці. Це поя-снюється тим, що фактори виробництва не можуть пов-ністю замінювати один одно-го. Кожний з них не може робити те, що може інший, або, якщо й може, то гірше.
орма ізокванти (крива випукла до початку системи координат), показує, що гранична норма технологічного заміщення капіталу працею зростає при просуванні вниз уздовж ізокванти (рис. 7.5).
 К К1К2=К2К3=К3К4=К4К5
К К1К2=К2К3=К3К4=К4К5L1L2< L2L3
 К1
К1
 К2
К2
 К3
К3
 К4
К4
 К5
К5 О L1 L2 L3 L4 L5 L
О L1 L2 L3 L4 L5 LРис. 7.5. Зростання граничної норми технологічного заміщення капіталу працею (МRТSKL)
Зростаюча гранична норма технологічного заміщення капіталу працею властива для більшості виробничих процесів, але існують деякі винятки, де ця залежність дещо інша.
І. Фактори виробництва можуть використовуватись лише в певній пропорції. Прикладом є співвідношення автомобілів і водіїв. Якщо кількість автомашин незмінна, то збільшення кількості шоферів не призведе до зростання обсягів продукції. І навпаки, збільшення кількості автомобілів, при фіксованій кількості шоферів також не покращить ситуацію. Аналогічні приклади можна знайти і в промисловості, і в сільському господарстві та в інших галузях і видах виробництва, де співвідношення між факторами виробництва є фіксованим. Ізокванта в цьому випадку матиме вигляд прямого кута, а гранична норма технологічного заміщення буде дорівнювати нулю (рис. 7.6).

2. Повне заміщення факторів виробниц-тва. За такої умови ізокванта має виг-ляд прямої з постійним нахилом. Од-нак в реальному житті така ситуація не трапляється. Адже при абсолют-ній взаємозамінності факторів вироб-ництва можна було б виробити увесь загальнодержавний обсяг певної про-дукції на одному заводі лише збіль-шуючи кількість працюючих.
K


Q3
Q2
Q1
 L
LРис. 7.6. Ізокванти при фіксова-ному співвідношенні факторів виробництва
7.3. Пропорційна варіація факторів виробництва
В
 довгостроковому періоді всі фактори виробництва є змінними. Підприємство намагаючись збільшити обсяги виробництва продукції, залучає все більше ресурсів, тобто збільшує масштаб виробництва. При цьому спостерігається різна віддача (ефект) від зміни масштабу виробництва.
довгостроковому періоді всі фактори виробництва є змінними. Підприємство намагаючись збільшити обсяги виробництва продукції, залучає все більше ресурсів, тобто збільшує масштаб виробництва. При цьому спостерігається різна віддача (ефект) від зміни масштабу виробництва.
Зростаюча віддача від масшта-бу має місце, коли обсяг вироб-ництва продукції зростає відчут-ніше, ніж обсяги використання ресурсів. Наприклад, при подвоєнні факторів виробництва, обсяг ви-пуску продукції зростає більш ніж у два рази (рис. 7.7).
K

2

 0
0Q=300
1

 5
5 1
 0 Q=200
0 Q=200Q=100
 10 15 20 L
10 15 20 L Рис. 7.7. Зростаючий ефект масш-табу виробництва
Зростаючий ефект масштабу виробництва може досягатися завдяки впливу таких факторів:
1. Поділ праці. На більших підприємствах можлива спеціалізація, що приво-дить до підвищення продуктивності праці і зниження витрат.
2. Поліпшення управління. На більших підприємствах виділяють спеціаліс-тів, які безпосередньо займаються маркетингом, рекламою, постачанням, науково-технічною роботою і т.д. Це дає змогу збільшити ефективність діяльності підприємства.
3. Збільшення масштабів виробництва не вимагає пропорційного збіль-шення всіх ресурсів. Наприклад, збільшення вдвічі кількості верстатів на заводі не вимагає такого ж збільшення механіків, електриків, охоронців, бухгалтерів, а також витрат на освітлення, опалення, вентиляцію і т.д.
П
Спадна віддача від масшта-бу виробництва має місце, коли випуск продукції зростає менш відчутніше, ніж зростають обся-ги використаних факторів вироб-ництва. Наприклад, збільшення вдвічі ресурсів приводить до підвищення випуску продукції лише в півтора рази (рис. 7.8).
 остійна (стала) віддача від масштабу виробництва спостерігається тоді, коли обсяги виробництва продукції і обсяги використання ресурсів зростають пропорційно. Збільшення вдвічі ресурсів виробництва приводить до подвоєння обсягів випуску продукції.
остійна (стала) віддача від масштабу виробництва спостерігається тоді, коли обсяги виробництва продукції і обсяги використання ресурсів зростають пропорційно. Збільшення вдвічі ресурсів виробництва приводить до подвоєння обсягів випуску продукції.  K
K


 20
20 
 15 Q=150
15 Q=1501
 0 Q=130
0 Q=130 Q=100
Q=10020 30 40 L
Рис. 7.8. Спадний ефект масштабу виробництва
Спадний ефект масштабу виробництва виникає через вплив наступних факторів:
Значна інерція великих систем, втрата ними гнучкості, необхідної в умовах нестабільного ринку.
Вихід підприємства за межі порогу керованості (великі розміри підпри-ємства створюють громіздку систему управління, затруднюється координація проміжних ланок, обмін інформацією, а це приводить до зниження ефективності управлінських рішень).
7.4. Оптимум виробника
Якщо в процесі виробництва використовують лише два змінних фактори: праця (L) та капітал (К) по відповідних цінах (PL і РK) то сукупні витрати (ТС) можна визначити за формулою: ТС =РLL+PKК
При фіксованих цінах на фактори виро-бництва можна знайти безліч різних наборів капіталу і праці, які можна придбати за ті самі сукупні витрати. Графічне зображення таких наборів називається ізокостою (рис. 7.9). Ізокоста – це лінія, що характери-зує комбінації витрат змінних факторів при фіксованих витратах виробництва.
К
 2
2К
 1
1ТС=200
ТС=100

О L1 L2 L
Рис. 7.9. Ізокоста
Властивості ізокости:
1. Кут нахилу ізокости залежить від цін на фактори виробництва. Оскільки tg α = K / L = PL / PK, то в точках перетину ізокости з вісями К (L=0) та L (К=0) сукупні витрати (ТС) визначаються за формулами відповідно:
а) для L = 0, ТС = РКК
б) для К = 0, ТС = PLL
З цих формул знаходимо К = ТС/РК, L = ТС/PL.
Звідси: tg α = K / L = ТС/РК * PL/TC = PL / PK, що й треба було довести.
З формули (7.6) випливає, що кут нахилу ізокости збільшується при зростанні ціни праці та зниженні ціни капіталу і, навпаки, кут нахилу ізокости зменшується при зниженні ціни праці та зростанні ціни капіталу (рис. 7.10).
 К К
К К
 К1
К1
а б
 ТС2 К2 ТС2 ТС1
ТС2 К2 ТС2 ТС1ТС1


О L1 L2 L О L
Рис. 7.10. Вплив цін на рух і нахил ізокости (а - зниження ціни праці; б - зростання ціни капіталу)
2. Всі точки ізокости відповідають однаковим сукупним витрата факторів виробництва.
3. Чим далі від початку координат розміщена ізокоста, тим більший обсяг ресурсів використовується у виробництві.
Я
Рівновага виробника - це такий його стан, при якому він не бажає змінювати співвідношення факторів виробництва (праці та капіталу), що задіяні у вироб-ничому процесі.
Умовою рівноваги є однаковий нахил ізокости та найбільшвіддаленої від початку координат ізокванти, що мають спільну точку (т. А на рис. 7.12).
к вже зазначалося, ізокоста - це множина альтернативних комбінацій витрат праці та капіталу, при яких витрати виробництва залишаються незмінними. Але яка ж з можливих комбінацій забезпечить найбільший обсяг виробництва продукції? Для вирішення цього питання потрібно сумістити ізокосту з картою ізоквант (рис. 7.4).

 K
K
А
Q3
Q2
Q1
 ТС L
ТС L Рис. 7.12. Рівновага виробника
Оскільки нахил ізокости визначається співвідношенням цін праці та капіталу, а нахил ізокванти – граничною нормою технологічного заміщення, то умову рівноваги можна записати як рівність:
МКТ8LK = РL/РK
А оскільки МКТ8LK = МРL/MРK, то:
МРL/MРK = РL/РK і МРL/РL= МРK/РK
Останнє рівняння відображає принцип найменших витрат, тобто стан, коли відношення граничних продуктів факторів виробництва (К, L) на одиницю вартості ресурсу (РL, РK) дорівнюють одне одному.
Я

Якщо з'єднати точки, що відпові-дають різним рівням сукупних витрат, то отримаємо траєкторію зростання (рис. 7.13).
Траєкторія зростання показує, як змінюється співвідношення факторів ви-робництва, що забезпечують мінімальні витрати, при збільшенні обсягів вироб-ництва продукції.
кщо така рівність не справджується, то підприємство може отримати приріст продукції без додаткових витрат за рахунок зміни співвідношення факторів виробництва.
 К
К


Q3
Q2
Q1

ТС1 ТС2 ТС3 L
Рис. 7.13. Траєкторія зростання
Контрольні запитання
Дайте визначення частинної варіації факторів виробництва. Наведіть приклади.
Охарактеризуйте залежність показників сукупного, середнього та граничного продуктів від змінного фактору на прикладі їх графіків.
Поясніть суть виробничої сітки.
Охарактеризуйте ізокванту та карту ізоквант.
Розкрийте економічний зміст граничної норми технологічного заміщен-ня факторів виробництва.
Поясніть чому гранична норма технологічного заміщення капіталу працею зростає при просуванні вниз уздовж ізокванти. Наведіть приклади винятків.
В чому полягає сутність ефекту масштабу виробництва?
Завдяки впливу яких факторів досягається зростаюча чи спадна віддача від масштабу виробництва?
Дайте визначення ізокости.
Охарактеризуйте властивості ізокости.
Розкрийте поняття рівноваги виробника, поясніть як вона досягається.
Дайте визначення траєкторії зростання.
Задачі
Для виробництва продукту підприємство використовує 20 одиниць капіталу та 16 одиниць праці. Яка гранична продуктивність праці, якщо гранична продуктивність капіталу дорівнює 4 (ефект масштабу при цьому має сталий характер).
2
АР
20

 . За допомогою рисунку дайте відпо-віді на питання:
. За допомогою рисунку дайте відпо-віді на питання: А
20


 ) Якщо АР=30 при L=15, а грани-чний продукт 16-ої одиниці праці дорівнює 10, то яка величина сукуп-ного продукту при L=16?
) Якщо АР=30 при L=15, а грани-чний продукт 16-ої одиниці праці дорівнює 10, то яка величина сукуп-ного продукту при L=16? Б
0 10 20 30 L
 ) Яким буде значення ТР, якщо АР=20?
) Яким буде значення ТР, якщо АР=20? 3. За даними виробничої сітки побудуйте ізокванти для Q = 70 і Q = 85. Обчисліть граничну норму технологічного взаємозаміщення капіталу працею для таких точок:
-
Капітал, од.
Праця, од.
1
2
3
4
5
1
20
40
55
65
70
2
40
60
70
80
85
3
55
70
85
100
100
4
65
80
100
110
115
5
70
85
105
115
120
а) для ізокванти Q = 70 – при переході від L=1 до L=3 та від L=3 до L=5;
б) для ізокванти Q = 85 – при переході від L=2 до L=3 та від L=3 до L=5.
4

 В Х
В Х