Курс лекций. Теория статистики Пособие для студентов, обучающихся по дистанционной системе Введение Статистика

• Название: Теория статистики Пособие для студентов, обучающихся по дистанционной системе Введение Статистика
• Анкор: Курс лекций
• Дата: 18.06.2022
• Размер: 2.79 Mb.
• Имя файла: Kurs_lekcij_dlya_distancionnogo_obucheniya (1).doc
• Тип: Реферат; #602460
• страница: 9 из 17

Общая дисперсия равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий:

,

Логика этого закона проста: общая дисперсия, возникающая под воздействием всех факторов, формируется из дисперсии, возникающей за счет фактора группировки и дисперсии, возникающей под воздействием всех прочих факторов.

С помощью закона сложения дисперсий можно оценить удельный вес факторов, лежащих в основе группировки, во всей совокупности факторов, воздействующих на результативный признак. Для этого применяется коэффициент детерминации, который рассчитывается как отношение факторной дисперсии к общей дисперсии результативного признака:



Корень квадратный из коэффициента детерминации называют эмпирическим корреляционным отношением:

.

Эмпирическое корреляционное отношение показывает какую часть общей колеблемости результативного признака определяет изучаемый фактор, то есть характеризует влияние группировочного признака на результативный признак. Этот показатель принимает значения в интервале [0,1]. Если связь отсутствует, то  = 0. В этом случае дисперсия групповых средних равна нулю (² = 0), то есть все групповые средние равны между собой и межгрупповой вариации нет. Это означает, что группировочный признак не влияет на вариацию исследуемого признака х. Если связь функциональная, то  = 1. В этом случае дисперсия групповых средних равна общей дисперсии (² = ²), то есть не будет внутригрупповой дисперсии. Это означает, что группировочный признак полностью определяет вариацию изучаемого признака а влияние прочих факторных признаков равно нулю. Промежуточные значения  оцениваются по степени их близости к предельным.

Качественная оценка связи между признаками

	Связь		Связь
0 0-0,2 0,2-0,3 0,3-0,5	Отсутствует Очень слабая Слабая Умеренная	0,5-0,7 0,7-0,9 0,9-0,99 1	Заметная Тесная Весьма тесная Функциональная

Пример. Рассчитать дисперсию, коэффициент детерминации и эмпирическое корреляционное отношение по данным таблицы.

Группировка населения отдельных областей России по среднему размеру ежемесячных денежных льгот пенсионеров

Место проживания	Средний размер денежных льгот	Численность пенсионеров, тыс.чел.	Дисперсия льгот в области (группе)
Курская обл. Курганская обл. Камчатская обл.	264,3 310,4 490,4	341,4 235,5 38,9	9025 2704 2116
Итого	296,2	615,8	7171,2

Сначала найдем средний размер льгот по трем областям в целом: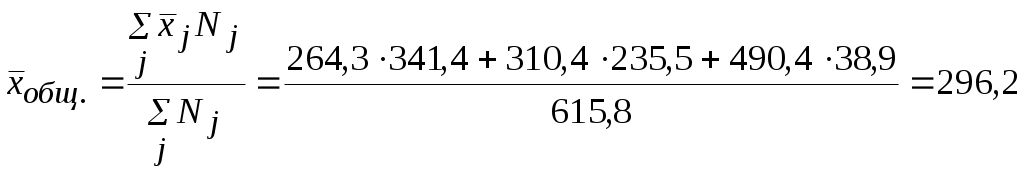



Вариация льгот по отдельным областям, обусловленная различием в местах проживания пенсионеров, характеризуется межгрупповой дисперсией:



Средняя из групповых дисперсий дает обобщающую характеристику случайной вариации, обусловленную отдельными факторами, кроме места проживания пенсионеров (например, характером занятости, стажем работы и т.п.):



Вариация льгот в изучаемых областях России, обусловленная влиянием всех факторов, вместе взятых, определяется общей дисперсией:



отсюда



Полученный коэффициент детерминации показывает, что дисперсия льгот зависит от места проживания пенсионеров на 32,5 %. Остальные 67,5% определяются множеством других неучтенных факторов.



Полученное значение эмпирического корреляционного отношения позволяет утверждать, что существует заметная связь между местом проживания пенсионеров и размером льгот.

Пример. Большая торговая компания заказала опрос, цель – выяснение влияния фактора повышения квалификации на результаты работы агентов по продажам. Опрос 8 торговых агентов дал следующие результаты:

Агент	Проходил ли переобучение в последние три года	Число контрактов, заключенных в день опроса
1	Да	9
2	Нет	8
3	Нет	6
4	Да	8
5	Нет	7
6	Да	8
7	Да	8
8	Нет	6

Среднее число контрактов, заключенных агентами:

.

В данном примере переподготовка – факторный признак, а число заключаемых контрактов – результативный.

Сгруппируем эти данные по признаку переобучения и рассчитаем средние по каждой группе.

Группы агентов	Число агентов	Число контрактов	Групповая средняя
Прошли переобучение	4	9, 8, 8, 8	8,25
Не прошли переобучение	4	8, 6, 7, 6	6,75

,

где n1 – число признаков в первой группе.

Или по формуле для взвешенных вариант

,

где f_i – частоты ряда.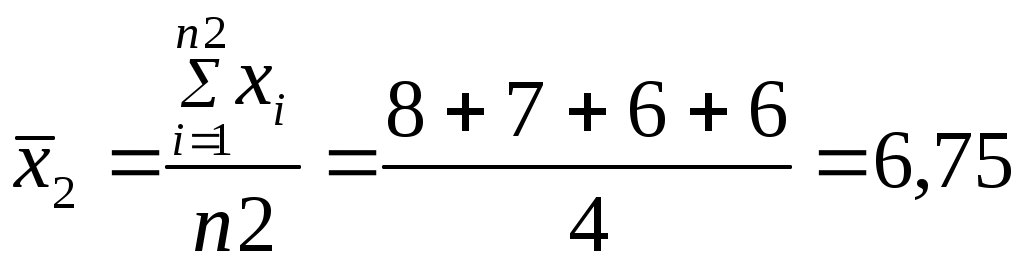

,

где n₂ – число признаков во второй группе.

Рассчитаем дисперсию в каждой группе.

Дисперсия числа заключенных контрактов у агентов, прошедших переобучение:

Число контрактов Х	Частота f
9 8	1 3	0,75 - 0,25	0,5625 00625	0,5625 0,1875
Итого	4	-	-	0,7500

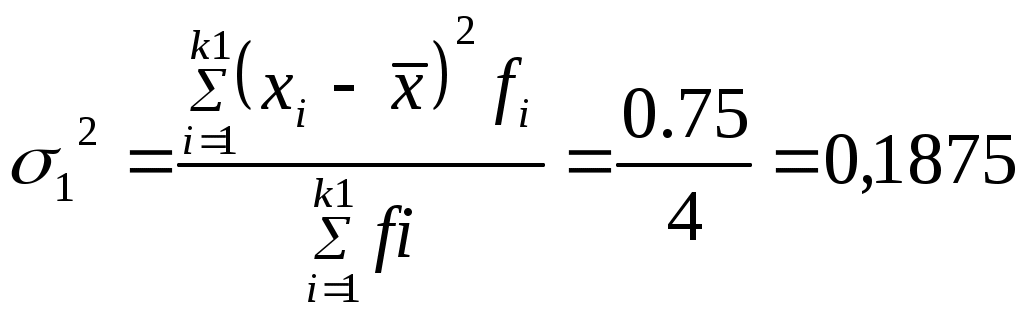Дисперсия числа заключенных контрактов у агентов, не прошедших переобучение:

Число контрактов Х	Частота f
8 7 6	1 1 2	1,25 0,25 - 0,75	1,5625 0,0625 0,5625	1,5625 0,0625 1,1250
Итого	4	-	-	2,7500

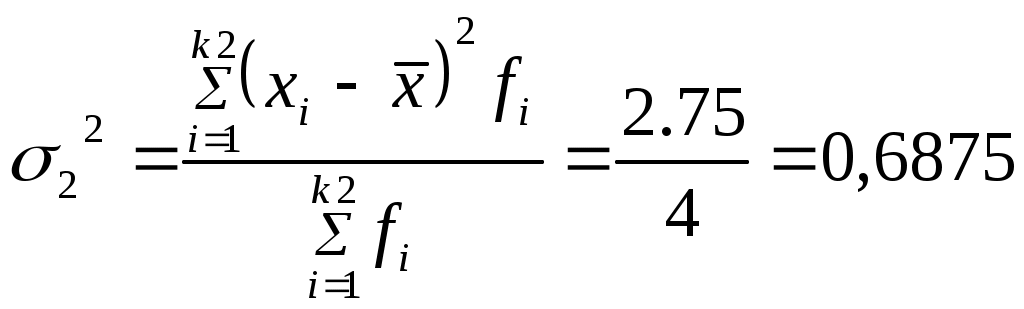Рассчитаем среднюю из внутригрупповых дисперсий:



Этот показатель характеризует влияние на результативный признак всех прочих факторных признаков за исключением признака, положенного в основу группировки.

Очевидно, что различие в числе заключенных контрактов в двух группах вызвано тем, что брокеры первой группы прошли переобучение, а брокеры второй группы не прошли. Найдем дисперсию между группами (межгрупповую дисперсию). Согласно формуле :

Этот показатель характеризует влияние на результативный признак факторного признака, положенного в основу группировки.

Общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:



Проверим верность правила сложения дисперсий. Рассчитаем общую дисперсию числа заключенных контрактов

Число контрактов х	Частота f
9 8 7 6	1 4 1 2	1,5 0,5 -0,5 -1,5	2,25 0,25 0,25 2,25	2,25 1,00 0,25 4,50
Итого	8	-	-	8,00

² = 8/8 = 1,00

В самом деле, 1,00 = 0,5625 + 0,4375.

По данным примера эмпирическое корреляционное отношение равно:



Следовательно, фактор, положенный в основу группировки, существенно влияет на число заключаемых агентами контрактов, но существуют и другие факторы, влияние которых тоже заметно.