Курс лекций. Теория статистики Пособие для студентов, обучающихся по дистанционной системе Введение Статистика
 Скачать 2.79 Mb.
|
6.3. Вариация альтернативного признакаСреди признаков, изучаемых статистикой, есть такие, которые принимают лишь два взаимно исключающих значения. Это – альтернативные признаки. Им придается соответственно два значения: 1 и 0. Частостью варианта 1 (она обозначается  ) является доля единиц, обладающих данным признаком, в общей численности совокупности. Разность  является частостью варианта 0. Таким образом:
Средняя арифметическая альтернативного признака  Дисперсия альтернативного признака  ,то есть дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком, и доли единиц, не обладающим этим признаком. Если значения 1 и 0 встречаются одинаково часто, то дисперсия достигает своего максимума  Правило сложения дисперсий распространяется и на дисперсии доли признака, то есть доли единиц с определенным признаком в совокупности, разбитой на группы. Внутригрупповая дисперсия доли определяется по формуле  Средняя из внутригрупповых дисперсий рассчитывается так:  Формула межгрупповой дисперсии имеет следующий вид:  где ni – численность единиц в отдельных группах; рi – доля изучаемого признака во всей совокупности, которая определяется по формуле:  Общая дисперсия определяется по формуле  Три вида дисперсий объединены между собой следующим образом:  Это – правило сложения дисперсии доли признака. Пример. Имеются следующие данные об удельном весе основных рабочих в трех цехах фирмы: Удельный вес основных рабочих фирмы
1) Определим долю рабочих в целом по фирме (формула 4)  2) Общая дисперсия доли основных рабочих по всей фирме в целом будет равна ( формула 5)  3) Внутрицеховые дисперсии рассчитаем, применив формулу 1 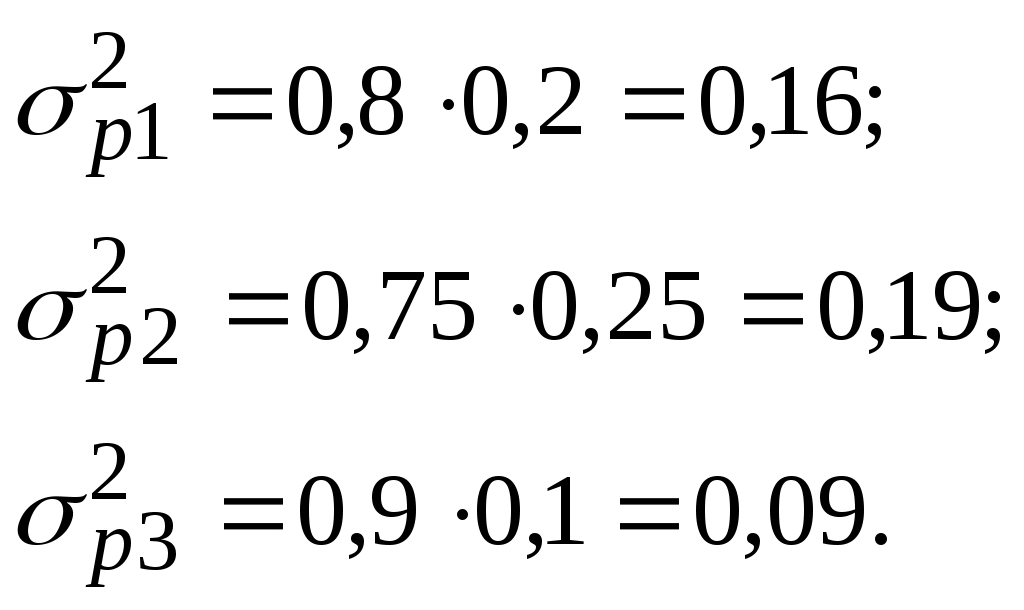 4) Средняя из внутригрупповых дисперсий будет равна (формула 2 )  5) Межгрупповую дисперсию определим по формуле 3  Проверка вычислений показывает: 0,154 = 0,15 + 0,004. Контрольные вопросы к теме «Показатели вариации» Чем вызвана необходимость изучения вариации признака? Укажите основные показатели вариации. Какие вам известны способы расчета дисперсии и среднего квадратического отклонения? Как определяется дисперсия альтернативного признака? Что такое коэффициент вариации? Правило сложения дисперсий. Что показывают частная (внутригрупповая), средняя из частных, межгрупповая и общая дисперсии? Как рассчитываются и что характеризуют коэффициент детерминации и эмпирическое корреляционное отношение? Контрольные задания к теме «Показатели вариации» Дисперсия признака равна 600. Объем совокупности равен 10. Сумма квадратов индивидуальных значений признака равна 6250. Найти среднюю величину. Средняя величина в совокупности равна 15, среднее квадратическое отклонение равно 10. Чему равен средний квадрат индивидуальных значений этого признака? Средняя величина в совокупности равна 13, а средний квадрат индивидуальных значений этого признака равен 174. Определить коэффициент вариации. Дисперсия признака равна 360000, коэффициент вариации равен 50%. Чему равна средняя величина признака? Дисперсия признака равна 360, средний квадрат индивидуальных значений равен 585. Чему равна средняя? Определить дисперсию признака, если средняя величина признака равна 2600, а коэффициент вариации признака равен 30%. Общая дисперсия равна 8,4. Средняя величина признака для всей совокупности равна 13. Средние по группам равны соответственно 10, 15 и 12. Численность единиц в каждой группе составляет 32, 53, и 45. Определить среднюю внутригрупповую дисперсию. По совокупности, состоящей из 100 единиц, известны: средняя арифметическая – 47,0; сумма квадратов индивидуальных значений признака–231592. Определить, однородна ли изучаемая совокупность. Определить величину эмпирического корреляционного отношения, если общая дисперсия равна 15,2; групповые средние  ;  , а численность групп соответственно равны 75, 60 и 65.Для изучения уровня заработной платы рабочих на предприятии обследовано 500 мужчин и 300 женщин. Результаты исследования показали, что у мужчин средняя заработная плата составила 1200 у.е. при среднеквадратическом отклонении 200 у.е., у женщин соответственно 800 у.е. и 150 у.е. Определить: 1) среднюю заработную плату работников; 2) дисперсии заработной платы и коэффициент вариации; 3) коэффициент детерминации и эмпирическое корреляционное отношение. Имеются данные о чистой прибыли (балансовой за вычетом налогов) предприятий двух районов:
Определите дисперсии чистой прибыли: групповые (по каждому району), среднюю из групповых, межгрупповую и общую. Имеются данные о заработной плате по двум группам работников:
Найти все виды дисперсий заработной платы, коэффициент детерминации и эмпирическое корреляционное отношение. Имеются следующие данные о среднем ежедневном времени занятости семейных женщин в домашнем хозяйстве:
Найти общую дисперсию занятости, коэффициент детерминации и эмпирическое корреляционное отношение. Есть две группы людей с разным месячным доходом (тыс. руб.): Группа А: 3, 3, 3, 4. Группа Б: 6, 6, 7. В какую группу нужно отнести человека с доходом 5 тыс. руб. в месяц. По результатам маркетингового исследования туристических фирм, организующих недельные туры в Турцию в различные курортные города, получены следующие данные о вариации стоимости туров (цены приведены для гостиниц одного класса):
Найти общую дисперсию, коэффициент детерминации и эмпирическое корреляционное отношение. По данным выборочного обследования заработной платы работников бюджетной сферы получены следующие показатели:
Определить: 1) среднюю заработную плату работников по двум отраслям; 2) дисперсии заработной платы; 3) коэффициент детерминации и эмпирическое корреляционное отношение. Имеются следующие данные (условные) по трем группам рабочих:
Рассчитать: 1) среднюю заработную плату всей совокупности рабочих; 2) дисперсии заработной платы; 3) коэффициент детерминации и эмпирическое корреляционное отношение. При изучении бюджета времени студентов было проведено обследование учащихся ВУЗов. При обследовании ВУЗы были разбиты на 7 групп по специализации. Были получены следующие результаты среднего количества времени, затрачиваемого студентами ежедневно на самостоятельную работу:
Используя правило сложения дисперсий определить зависимость между средним числом часов на самостоятельную работу от специализации студента. Для определения средней величины расходов на полугодовую подписку на газеты и журналы обследуемая совокупность семей разбита на группы по уровня дохода на три группы. По группам получены следующие результаты:
Определите все виды дисперсий расходов, коэффициент детерминации и эмпирическое корреляционное отношение. В районе 20 тыс. семей, проживающих в городах, поселках городского типа и сельской местности. В результате были получены следующие данные о среднем числе детей в семьях:
Используя правило сложения дисперсий определите коэффициент детерминации и эмпирическое корреляционное отношение. Имеются следующие выборочные данные о вкладах населения района:
Определите тесноту связи между средним размером вклада и типом населения, исчислив коэффициент детерминации и эмпирическое корреляционное отношение. Капитал коммерческих банков характеризуется следующими данными:
Определите показатели тесноты связи между размером собственного капитала банков и привлеченными средствами, исчислив коэффициент детерминации и эмпирическое корреляционное отношение. Тема 7. Виды и формы связей, различаемые в статистике
6.1. Виды и формы связей, различаемые в статистике Современная наука об обществе объясняет суть явлений через изучение их взаимосвязи. Например, объем валютных торгов зависит от спроса на валюту, который в свою очередь определяется состоянием экономики, активностью внешнеэкономической деятельности субъектов и др., объем продукции предприятия связан с численностью работников, стоимостью основных фондов и т.д. Различают два типа взаимосвязей между различными явлениями и их признаками: функциональную или жестко детерминированную и статистическую или стохастически детерминированную. Функциональная жестко детерминированная связь – это вид причинной зависимости, при которой определенному значению факторного признака соответствует одно или несколько точно заданных значений результативного признака. Этот вид связи встречается чаще в естественных науках, но так же и в экономике. Например, при простой сдельной оплате труда связь между оплатой труда y и количеством изготовленных изделий x при фиксированной расценке за одну деталь, например, 7 руб. можно выразить формулой y = 7x Стохастическая связь – это вид причинной зависимости, проявляющейся не каждом отдельном случае, а в общем, среднем, при большом числе наблюдений. Среди взаимосвязанных признаков одни могут рассматриваться как определенные факторы, влияющие на изменение других, а вторые как следствие, результат влияния первых. Соответственно первые, то есть признаки, влияющие на изменение других, называют факторными, а вторые – результативными. Стохастические взаимосвязи могут быть изучены различными способами. Наиболее известный из них метод изучения корреляционных связей. Корреляционная связь (от английского слова correlation – соотношение, соответствие) - частный случай стохастической связи, состоящей в том, что c изменением факторного признака (х) закономерным образом изменяется среднее значениерезультативного признака (y), в то время как в каждом отдельном случае y может принимать множество различных значений. Корреляционная связь между признаками может возникать различными путями. Важнейший путь – взаимосвязь вариации результативного признака с вариацией факторного признака. Обычно в этом случае говорят о взаимосвязи признаков. Например, y – урожайность сельскохозяйственной культуры, х – балл оценки плодородия почв. Либо, y – сумма налоговых поступлений в региональный бюджет, x – выручка от реализации продукции. Здесь совершенно логически ясно, какой признак выступает как независимая переменная (фактор), какой как зависимая переменная ( результат). По направлению выделяют связь прямую и обратную (положительную и отрицательную), По аналитическому выражению линейную и нелинейную. Изучение корреляционных связей сводится в основном к решению следующих задач: выявление наличия (или отсутствия) связи между изучаемыми признаками; измерение степени тесноты связи между признаками; нахождение аналитического выражения связи, отражающей зависимость между х и у; экономическая интерпретация и практическое использование полученного результата. В начальной стадии анализа статистических зависимостей применяются простейшие методы оценки наличия связи, её направления и характера, выявляется форма воздействия одних факторов на другие. Для этих целей применяются методы приведения параллельных данных; графический и аналитических группировок. Метод приведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и получить представление о её характере. Пример 1. Предположим, мы имеем данные о выпуске продукции на 6 однотипных предприятиях (х) и потреблении на них электричества (у): Сравним изменения двух величин: Таблица 1. Зависимость потребления электричества от объема выпуска продукции
Таблица наглядно демонстрирует, что с увеличением х возрастает и у, поэтому связь между ними считать прямой. Графический метод используется для наглядного изображения формы связи между изучаемыми признаками. Для этого в прямоугольных осях координат строят график, по оси y, которого откладывают индивидуальные значения результативного признака, а по оси х – индивидуальные значения – факторного. Полученная совокупность точек называется полем корреляции. 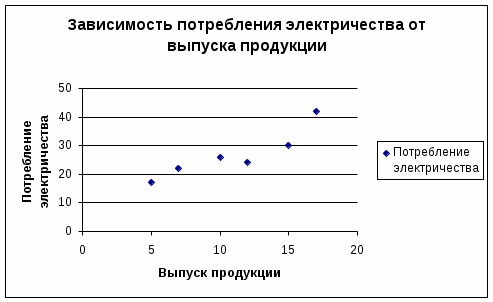 График, построенный по индивидуальным значениям признаков Примера 1, указывает на то то, что связь носит приблизительно линейный характер. Метод аналитических группировок. В теме группировка мы уже говорили, что при аналитической группировке исследуется связь между двумя и более признаками, из которых один рассматривается как результат, другой (другие) как фактор (факторы). Для установления связи между признаками данные группируются по признаку-фактору, который располагается в подлежащем аналитической таблицы. Изменения факторного признака при переходе от одной группы к другой вызывают соответствующие изменения результативного признака. Таблица 2. Характеристика зависимости прибыли малых предприятий от оборачиваемости оборотных средств на 200__ год
Оборачиваемость в днях – фактор, обозначаемый обычно х, а прибыль – результат – y. Таблица ясно демонстрирует присутствие связи между признаками, это – обратная (отрицательная) связь. 6.2. Измерение тесноты связи в случае корреляционной зависимости. Большинство методов измерения тесноты связи заключается в сопоставлении отклонений значений признаков от их средних. Это основано на предположении, что при полной независимости признаков отклонения значений факторного признака от средней  носят случайный характер и должны случайно сочетаться с различными отклонениями  . При наличии значительного перевеса совпадений или несовпадений таких отклонения делается предположение о наличии связи между х и y. Один из простейших показателей тесноты связи разработан австрийским психиатром Г.Фехнером: 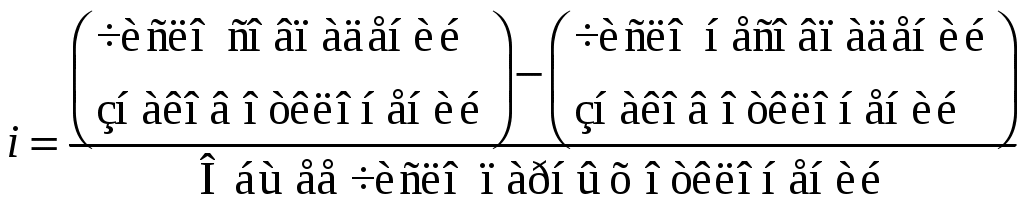 Показатель Фехнера изменяется от [-1;1], при значении равном 1 он указывает на полную прямую связь, при значении –1 на полную обратную связь, при i=0 связь отсутствует. Промежуточные значения i характеризуют степень близости связи к функциональной. Например, для данных примера 1 рассчитаем средние значения для х и у:   Таблица 3. Расчет коэффициента Фехнера для оценки степени зависимости потребления электричества от объема выпуска продукции
  Можно считать связь достаточно сильной. Недостаток показателя Фехнера состоит в том, что разные по абсолютной величине отклонения имеют одинаковый вес. Самый известный измеритель тесноты связи между признаками - линейный коэффициент корреляции Пирсона (назван по имени английского статистика К.Пирсона, введшего это коэффициент в научный анализ), он характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости. Что представляет собой этот коэффициент? Вновь используем для расчета данные примера 1. Запишем расчеты в виде среднего значения совместных отклонений признаков от их средних значений: 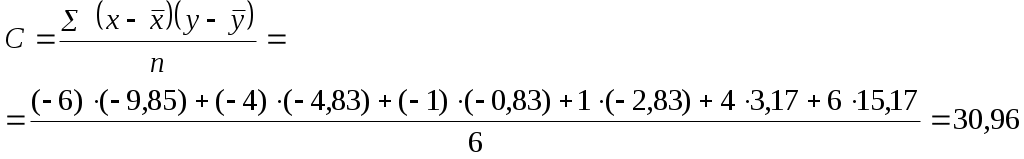 Полученное значение называется коэффициентом ковариации. Это – мера совместной вариации признаков. Или мы можем сказать, что это – мера соответствия вариации результативного признака вариации факторного. Недостатком коэффициента ковариации является то, что он не нормирован. Для преодоления этого недостатка можно полученное выражение разделить на среднее квадратическое отклонение по х и по y.   Полученное значение – линейный коэффициент корреляции, показатель интенсивности линейной связи. Это - безразмерная величина, которая изменяется в интервале от –1 до +1,  . Существует эмпирическое правило, согласно которому качественная оценка связи между признаками производится по шкале Чеддока:
Путем ряда преобразований можно получить следующие аналитические выражения для коэффициента корреляции:   Производя расчет по итоговым значениям исходных переменных, линейный коэффициент корреляции можно вычислить по формуле: 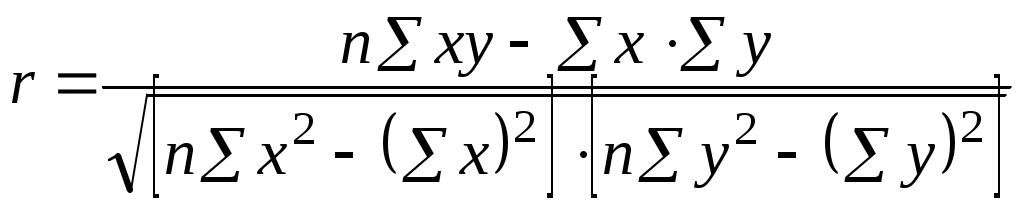 Линейный коэффициент корреляции имеет большое значение при исследовании социально-экономических явлений и процессов, распределения которых близки к нормальному. 6.3. Оценка достоверности коэффициента корреляции Коэффициент линейной корреляции, исчисленный по выборочным данным является случайной величиной. Полученный из выборки коэффициент корреляции r является оценкой коэффициента корреляции в генеральной совокупности. С уменьшением числа наблюдений надежность коэффициента корреляции падает. Оценка существенности (значимости) линейного коэффициента корреляции основана на сопоставлении значения r с его средней квадратической ошибкой  : , При оценке значимости коэффициента корреляции обычно рассматриваются следующие ситуации. Если число наблюдений достаточно велико (обычно свыше 30), а значение коэффициента корреляции не превышает 0.9, распределение коэффициента корреляции r можно считать приближенно нормальным со средней квадратической ошибкой  , При достаточно большом числе наблюдений r должен превышать свою среднюю ошибку не менее, чем в три раза:  . Если это неравенство не выполняется, то существование связи между признаками нельзя считать доказанным. Задавшись определенной вероятностью, можно построить доверительные границы r:  Так, например, при вероятности 0,95, для которой t= 1,96, доверительные границы составят  ,При вероятности 0,997, для которой коэффициент доверия t= 3, доверительные границы составят  Поскольку значение r не может превышать единицу, то в случае, если  > 1, следует указать только нижний предел, то есть утверждать, что реальный r не меньше, чем  . 2. Для малого объема выборки, с распределением r далеким от нормального, применяются другие методы оценки значимости коэффициента корреляции. При небольшом числе наблюдений (n < 30), средняя ошибка линейного коэффициента корреляции находится по формуле:  а значимость проверяется на основе t критерия Стьюдента. При этом выдвигается гипотеза о равенстве коэффициента корреляции нулю, то есть об отсутствии связи между y и x в генеральной совокупности. Для этого используется статистика:  расчетное значение которой сопоставляется с табличным, из таблиц распределения Стьюдента. Если нулевая гипотеза верна, то есть r=0, то распределение t- критерия подчиняется закону распределения Стьюдента с n-2 степенями свободы и принятым уровнем значимости  (обычно 0,05). В каждом конкретном случае по таблице распределения t-критерия Стьюдента находится табличное (критическое) значение t, которое допустимо при справедливости нулевой гипотезы, и с ним сравнивается фактическое (расчетное) значение t. Если tрасч. > t табл. , то нулевая гипотеза отклоняется и линейный коэффициент считается значимым, а связь между xи y – существенной. И наоборот. 3. При малом числе наблюдений в выборке и высоком коэффициенте корреляции (распределение r отличается от нормального) для проверки гипотезы о наличии корреляционной связи, а также построения доверительного интервала применяется z-преобразование Фишера. Для этого рассчитывается величина  Распределение z приближается к нормальному. Вариация z выражается формулой  Рассчитаем z критерий для примера 1, поскольку в этом случае мы имеем небольшое число наблюдений и высокий коэффициент корреляции.  .Чтобы не вычислять значения логарифмов, можно воспользоваться специальными таблицами Z-преобразований (Ефимова М.Р. стр. 402, Шмойлова Р.А. стр.446, Елисеева И.И. стр.473). Находим, что коэффициенту корреляции 0,94 соответствует Z=1,74. Находим  Отношение Z к средней квадратической ошибке равно 3. Таким образом, мы можем полагать действительное наличие связи между величиной выпуска продукции и расходом электроэнергии для всей совокупности предприятий. 6.4. Ранговая корреляция Если n вариантов ряда расположены в соответствии с возрастанием или убыванием признака х, то говорят, что объекты ранжированы по этому признаку. Ранг для хiуказывает место, которое занимает i-е значение признака среди других n значений признака х (i=1,2,..n). Например, при исследовании рынка можно задаться целью выяснения предпочтений потребителей при выборе товара (при покупке акций, мороженного, водки и т.п.), таким образом, чтобы они распределили товар в порядке возрастания (или убывания) своих потребительских предпочтений. Если имеется два набора ранжированных данных, то можно установить степень линейной зависимости между ними. Предположим имеется 5 продуктов, которые ранжированы по порядку предпочтений от 1 до 5 в соответствии с двумя характеристиками А и В.
Для определения наличия взаимосвязи между ранговыми оценками используется коэффициент ранговой корреляции Спирмена. Его расчет основан на различиях между рангами. Обозначим D= ранг A – ранг B Коэффициент Спирмена равен:  , где n – число пар ранжированных наблюдений. В нашем примере мы имеем пять пар рангов, следовательно, n = 5. Cумма D2 равна: (2-1)2 + (5-3)2 + (1-2)2 + (3-4)2 + (4-5)2=1+4+1+1+1=8 Коэффициент Спирмена равен:  То есть мы нашли достаточно сильную линейную связь. Коэффициент Спирмена изменяется в интервале от [-1; 1] и интерпретируется так же как и коэффициент Пирсона. Разница лишь в том. что он вычисляется для ранжированных данных. Значимость коэффициента Спирмена проверяется на основе t критерия Стьюдента по формуле:  . (12). Значение коэффициента считается существенным, если tрасч. > tкрит. (; k = n-2). 6.5. Корреляция альтернативных признаков Альтернативные признаки – это признаки, принимающие только два возможных значения. Исследования их корреляции основано на показателях, построенных на четырехклеточных таблицах, в которые сводятся значения признаков.
Например, требуется измерить связь между прививками от гриппа и снижением заболеваемости гриппом в группе случайно выбранных студентов.
Вопрос: существует ли связь между заболеваемостью и прививками? Решение Для измерения тесноты взаимосвязи признаков производится расчет коэффициента контингенции по формуле:  (13) Коэффициент контингенции принимает значения на интервале [-1; 1]. Интерпретация аналогична коэффициенту корреляции. Мы получили слабую отрицательную связь, то есть Другой метод измерения связи основан на расчете коэффициента ассоциации:  (14) Минус перед коэффициентом говорит об обратном направлении связи, чем больше прививок, тем меньше заболеваний. Коэффициент контингенции всегда бывает меньше коэффициента ассоциации и дает более корректную оценку тесноты связи. Задача В результате обследования работников предприятия получены следующие данные (чел.)
Требуется оценить тесноту взаимосвязи между уровнем образования и удовлетворенностью своей работой с помощью коэффициентов контингенции и ассоциации. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
