Курс лекций. Теория статистики Пособие для студентов, обучающихся по дистанционной системе Введение Статистика
 Скачать 2.79 Mb. Скачать 2.79 Mb.
|
8.1. Основные понятия и показателиРяд расположенных во времени статистических данных, изменение которых отражает закономерность развития изучаемого явления, называется рядом динамики или временным рядом. Ряд динамики представляет собой числовые значения определенного статистического показателя в последовательные моменты или периоды времени. Числовые значения того или иного статистического показателя, составляющие ряд динамики, называют уровнями ряда и обычно обозначают через y. Моменты или периоды времени, к которым относятся уровни, обозначают через t. Таким образом временной ряд состоит из двух элементов: Ряды динамики, как правило, представляют в виде таблицы или графически. При графическом изображении ряда динамики на оси абсцисс строится шкала времени t, на оси ординат – шкала уровней ряда y. Например, Таблица 1. КРЕДИТНЫЕ ОРГАНИЗАЦИИ (на начало года)
Источник Россия в цифрах. 2006: Крат.стат.сб./Росстат- M., С.334 Построение и анализ рядов динамики позволяют выявить и измерить закономерности развития социально-экономических явлений во времени. Эти закономерности проявляются не четко на каждом уровне, а лишь в тенденции, в достаточно длительной динамике. На основную закономерность динамики, называемую трендом, накладываются случайные влияния, а так же носящие сезонный характер. Выявление основной тенденции – тренда - в изменении уровней ряда, а так же сезонной компоненты является одной из основных задач анализа рядов динамики. 8.2. Виды рядов динамики В зависимости от вида показателей ряды динамики подразделяют на ряды абсолютных, относительных и средних величин (показателей). Примером ряда абсолютных величин служит пример, представленный в таблице 1. На основе рядов абсолютных величин образуются ряды динамики относительных и средних величин. Ряды относительных величин могут характеризовать темпы роста или снижения определенного показателя, уровень рождаемости или смертности, примером ряда средних величин служат данные о среднегодовой численности занятых в экономике, о средней заработной плате и др. Временные ряды могут быть интервальными и моментными. Моментным называется ряд, уровни которого характеризуют значение показателя (явления) по состоянию на определенные моменты времени (дату). Например, таблица 1. Интервальным называется ряд, уровни которого характеризуют значение показателя, достигнутое за определенный период (интервал). Например, Таблица 2. Среднедушевые денежные доходы населения, руб. в месяц (до 2000 г. – тыс. руб.)
Источник Россия в цифрах. 2006: Крат.стат.сб./Росстат- M., С.29 Или Таблица 3. Среднегодовая численность занятых в экономике, млн. человек
С делением рядов на моментные и интервальные непосредственно связан способ расчета их среднего уровня. Поэтому во избежание ошибок при расчете средних уровней, надо четко представлять отличие интервальных рядов от моментных. Средний уровень интервального ряда с равными интервалами исчисляется по формуле простой арифметической: Среднегодовая численность занятых в экономике за одиннадцать лет с 1995 по 2005 гг. составила: Средний уровень моментного ряда исчисляется по формуле средней хронологической: 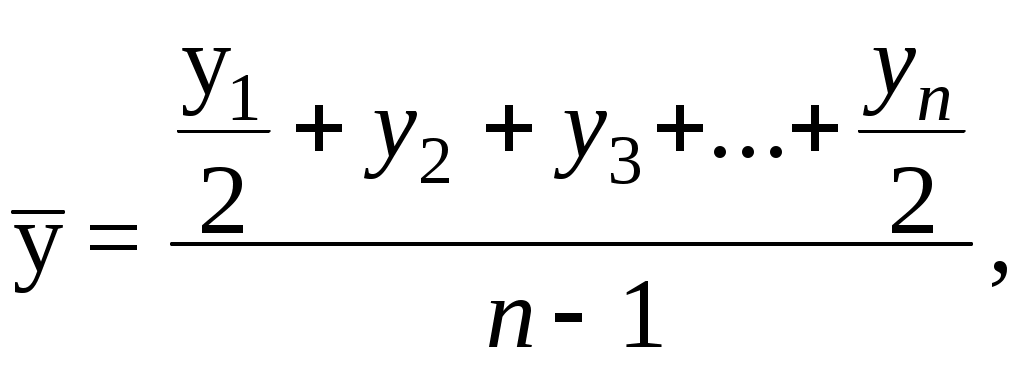 где y1 и yn - начальный и конечный уровни ряда, y2 , y3 ... - промежуточные уровни, n - число уровней ряда, принимаемых в расчет. Среднee число кредитных организаций за 6 лет с 2001 по 2006 гг. составило: 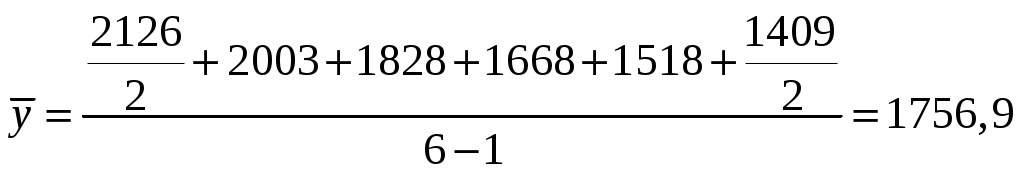 Обращаем внимание на то, что начальный уровень ряда здесь показан как y1 , а не y0 . 8.3. Показатели изменения уровней ряда динамики Большинство статистических характеристик ряда динамики основано на абсолютном или относительном сравнении его уровней. Сравниваемый уровень принято называть текущим, а уровень, с которым производится сравнение, - базисным. Показатели роста и прироста предназначены для характеристики изменения уровней ряда (yt ). Показатели роста представляют собой отношение двух уровней ряда, а прироста - их разность. Если эти показатели имеют вид относительных величин, их называют коэффициентами. Если они выражены в процентах - темпами. Они могут быть цепными и базисными. У цепных ведется сравнение текущего уровня с предыдущим, а у базисных - с начальным, принятым за базу. В качестве базисного выбирается либо начальный уровень ряда, либо уровень, с которого начинается какой-то новый этап развития явления. Пример 1. Рассчитать показатели роста и прироста для анализа динамики числа кредитных организаций Таблица . Кредитные организации (на начало года)
2001 – базисный год. 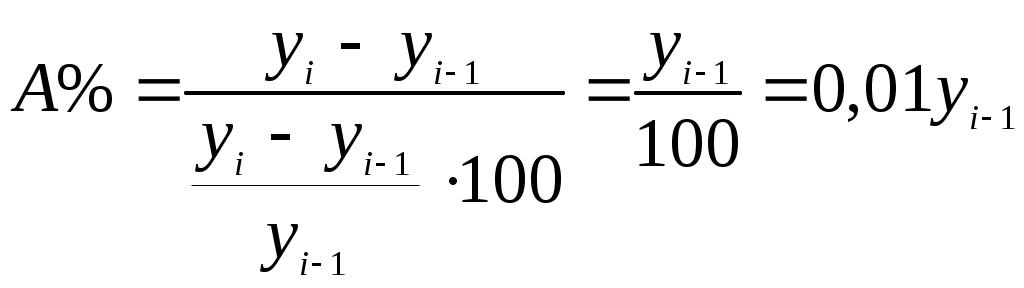 Абсолютное изменение уровней ряда измеряется показателем абсолютного прироста. Цепные показатели прироста исчисляются так: 2ц = y2 - y1 3ц = y3 - y2 4ц = y4 - y3 . . . iц = yi - yi-1 Базисные показатели прироста : 2б = y2 - y1 3б = y3 - y1 4б = y4 - y1 . . . iб = yi - y1 Абсолютный прирост характеризует увеличение или уменьшение уровней ряда за определенный промежуток времени. Абсолютные приросты с переменной базой (цепные) называют скоростью роста или первыми разностями. Цепные и базисные абсолютные приросты по данным примера 1 показывают сокращение (прирост) кредитных организаций и абсолютные изменения по сравнению с 2001 годом. Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, то есть общему приросту за весь промежуток времени. Для характеристики интенсивности, то есть относительного изменения уровней ряда динамики исчисляют коэффициенты или темпы роста (снижения). Цепные коэффициенты роста исчисляются следующим образом: К2/1ц = Цепные темпы роста будут иметь следующий вид: Т2/1ц=(K2/1ц)100%, T3/2ц= (K3/2ц)100%, …. Базисные же коэффициенты будут такими: К2/1б = Базисные темпы роста: T2/1б=(K2/1б)100%, T3/2б=(K3/2б)100% … Они показывают во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если коэффициент больше 1) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). (см. Пример 1) Между цепными и базисными коэффициентами роста существует взаимосвязь (если базисные коэффициенты исчислены по отношению к начальному уровню ряда динамики): произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь период, а частное от деления последующего базисного коэффициента роста на предыдущий уровень равно соответствующему цепному коэффициенту роста. Относительную оценку скорости изменения уровня ряда в единицу времени дают показатели коэффициентов (темпов) прироста. Темп прироста показывает на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения. Он представляет собой отношение абсолютного прироста к предыдущему или начальному (базисному) уровню. Цепной темп прироста: Т пр.ц.=(yц/yi-1)100% T пр.б.=( yб/y1)100% Темп прироста можно получить и из темпа роста, если из него вычесть 100%. Коэффициент прироста получается вычитанием 1 из коэффициента роста. При анализе динамики развития следует так же знать какие абсолютные значения скрываются за темпами роста и прироста. Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени зачастую показывает, что при снижении темпов прироста абсолютный прирост не всегда уменьшается, в отдельных случаях он может возрастать. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением (содержанием) одного процента прироста и рассчитывают как отношение абсолютного прироста к темпу прироста за тот же период времени, %: 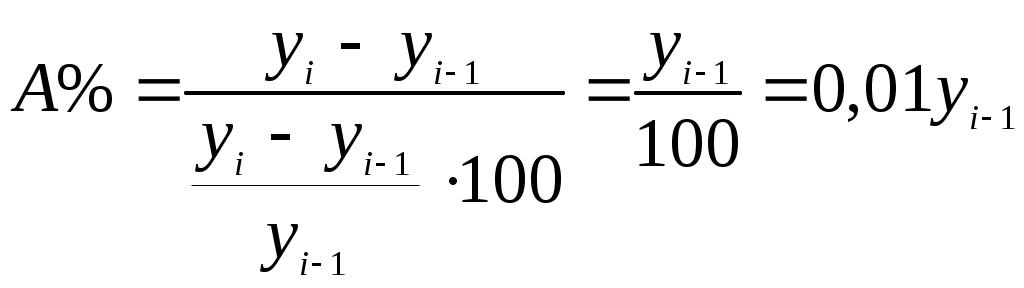 Абсолютное значение одного процента прироста показывает какое абсолютное значение скрывается за относительным показателем – одним процентом прироста (см. пример 1). В тех случаях, когда сравнение производится с отдалением периода времени, принятого за базу сравнения, рассчитывают, так называемые, пункты роста, которые представляют собой разность базисных темпов роста, %, двух смежных периодов. В отличие от темпов прироста, которые нельзя ни суммировать, ни перемножать, пункты роста можно суммировать, в результате получаем базисные темпы прироста. (см. пример 1). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
