Курс лекций. Теория статистики Пособие для студентов, обучающихся по дистанционной системе Введение Статистика
 Скачать 2.79 Mb. Скачать 2.79 Mb.
|
|
Данные о ценах и объемах реализации товара "X" в двух регионах
Проведем анализ изменения цен на данный товар. Из таблицы видно, что цена в каждом регионе возросла. Для сводной оценки этого роста воспользуемся средними показателями. Так как в данном случае реализуется один и тот же товар, вполне правомерно рассчитать его среднюю цену за июнь и за июль. Индекс цен переменного состава представляет собой соотношение средних значений за два рассматриваемые периода: 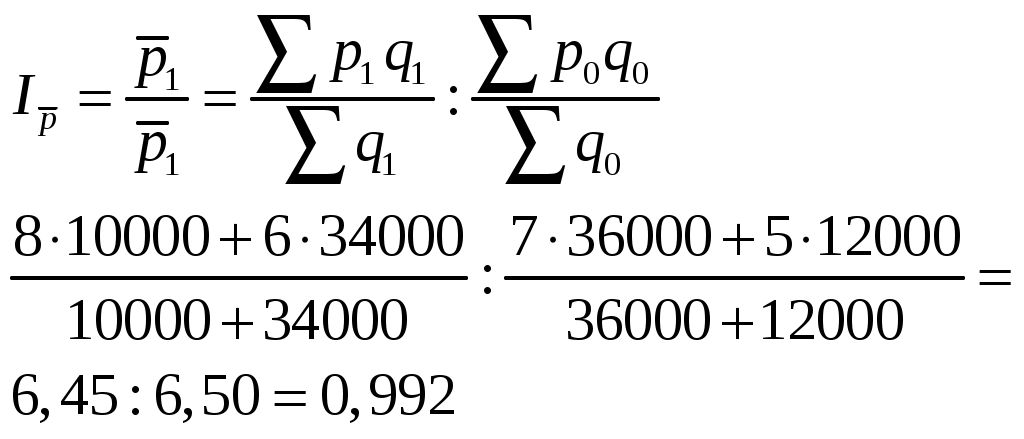 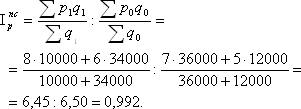 Рассчитанное значение индекса указывает на снижение средней цены данного товара на 0,8%, т.е. с 6,50 тыс. руб. до 6,45 тыс. руб. В то же время, из приведенной выше таблицы видно, что цена в каждом регионе в 2003 г. по сравнению с 2002 г. возросла. Данное несоответствие объясняется влиянием изменения структуры реализации товаров по регионам: в 2002 г. по более высокой цене продали товара втрое больше, а в 2003 г. ситуация принципиально изменилась (в данном условном примере для наглядности числа подобраны таким образом, чтобы это различие в структуре продаж было очевидным). Иными словами, на динамике средней цены данного товара отразились структурные сдвиги в рассматриваемой совокупности. Оценить воздействие этого фактора можно с помощью индекса структурных сдвигов: 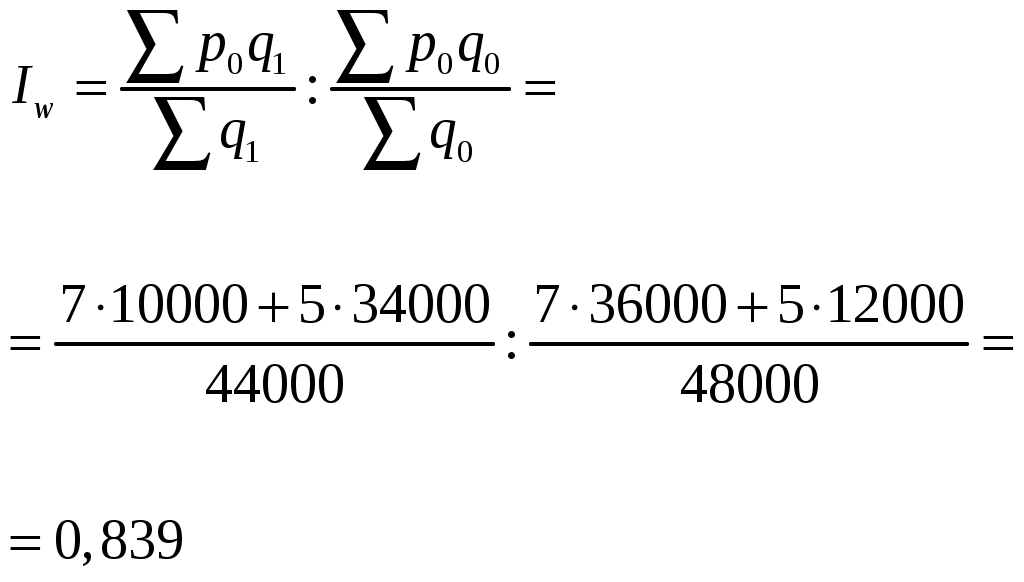 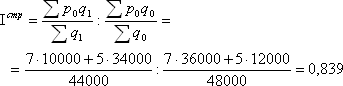 Первая формула в этом индексе позволяет ответить на вопрос, какой была бы средняя цена в 2003 г., если бы цены в каждом регионе сохранились на уровне предыдущего года. Вторая часть формулы отражает фактическую среднюю цену 2002 г. В целом по полученному значению индекса мы можем сделать вывод, что за счет структурных сдвигов цены снизились на 16,1%. Последним в данной системе является индекс цен фиксированного состава, который не учитывает влияние структуры: Полученное значение индекса позволяет сделать вывод о том, что если бы структура реализации товара "Х" по регионам не изменилась, средняя цена возросла бы на 18,3%. Однако, влияние на среднюю цену фактора структурных изменений оказалось сильнее и в итоге цена даже несколько снизилась. Данное взаимодействие рассматриваемых факторов отражается в следующей взаимосвязи: 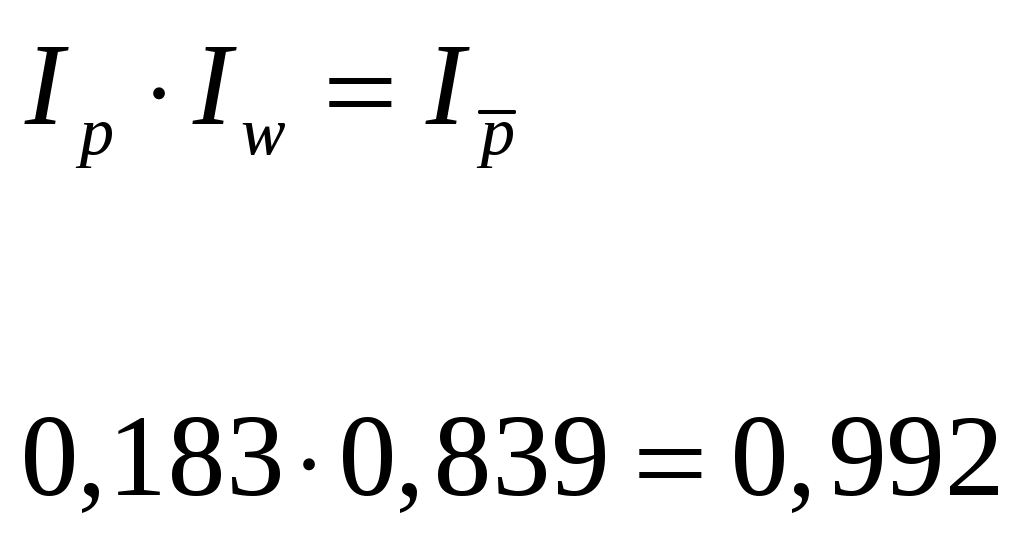 Аналогично строятся индексы структурных сдвигов, переменного и фиксированного состава для анализа изменения себестоимости, урожайности и других показателей. Ряды индексов с постоянной и переменной базой сравнения (цепные и базисные), с постоянными и переменными весами При изучении динамики общественных явлений за более или менее длительное время исчисляют не один, а ряд индексов, так называемая система индексов. Выбор базы сравнения и весов индексов - это два важнейших методологических вопроса построения систем индексов в тех случаях, когда сравниваемых периодов три и более. По базе сравнения различают цепные и базисные индексы. Система базисных индексов – это ряд последовательно вычисленных индексов одного и того же явления с постоянной базой сравнения, то есть в знаменателе всех индексов находится индексируемая величина базисного периода. Система цепных индексов – это ряд индексов одного и того же явления, вычисленных с меняющейся от индекса к индексу базой сравнения. Выбор системы индексов (базисные или цепные) проводится в зависимости от целей анализа. Базисные индексы дают более наглядную характеристику общей тенденции развития исследуемого явления, а цепные - четче отражают последовательность изменения уровней во времени. Системы цепных и базисных индексов могут быть построены для индивидуальных и общих инднксов. Cхема построения базисных индексов Исходные уровни: q1q2q3q4 базисные индексы: iq = Схема построения цепных индексов Исходные уровни: q1 Цепные индексы: ip = Между цепными и базисными индексами имеется взаимосвязь, которая заключается в следующем: произведение всех цепных индексов равно общему базисному индексу: Отсюда следует: отношение каждого последующего базисного индекса к предыдущему базисному дает промежуточный цепной индекс: Взаимосвязь цепных индексов в индивидуальных проявляется всегда, а в сводных (общих) индексах только при условии постоянства весов (или соизмерителей). Возьмем ряд цепных индексов с постоянными весами (р1): Iq= Если перемножить эти индексы, то получим общий базисный индекс: Этому требованию не отвечают индексы с переменными весами: Iq= Ряды индексов с постоянными и переменными весами Два и более индексов с одинаковыми по содержанию и во времени весами образуют ряд индексов с постоянным весами или соизмерителями: Iq= Два и более индексов с одинаковыми по содержанию, но различными во времени весами или соизмерителями называются рядом индексов с переменными весами или соизмерителями: Iq= В статистической практике ежегодные индексы объема промышленной продукции вычисляются как индексы с постоянными соизмерителями или весами, т.к. продукция оценивается в сопоставимых ценах. Ежегодные индексы физического объема продукции в торговле вычисляются как индексы с переменными весами или соизмерителями. Взаимосвязи индексов. Индексный метод выявления роли отдельных факторов динамики сложных явлений Многие статистические показатели, характеризующие различные стороны общественных явлений, находятся между собой в определенной связи (часто в виде произведения). Связь между экономическими показателями находит свое отражение и во взаимосвязи характеризующих их индексов. В общем случае, если z = yx, то Iz = IyIx, а если z = y/x, то и Iz = Iy/ Ix.. Поэтому многие, связанные между собой экономические показатели, образуют индексные системы. Система взаимосвязанных индексов дает возможность применять индексный метод для изучения взаимосвязи общественных явлений, проведения факторного анализа с целью определения роли отдельных факторов (не зависимых друг от друга) на изменение сложного явления В отечественной статистике практике принята следующая практика факторного анализа. Если результативный показатель можно представить как произведение объемного и качественного показателя, то, определяя влияние объемного фактора на изменение результативного показателя, качественный фактор фиксируют на уровне базисного периода. Если же определяется влияние качественного показателя, то объемный фактор фиксируется на уровне отчетного периода. Рассмотрим построение взаимосвязанных индексов на примере индексов цен, физического объема продукции (если речь идет об отпускных ценах промышленности) или физического объема товарооборота (если речь идет о розничных ценах) и индекса стоимости (товарооборота в фактических ценах). Индексы физического объема и цен являются факторными по отношению к индексу стоимости продукции (товарооборота в фактических ценах): Таким образом произведение нидекса цен наиндекс физического объема продукции дает индекс стоимости продукции (товароооборота в фактических ценах), то есть индексы образуют индексную систему из трех индексов. Если, например, по определенной группе товаров цена единицы товара в отчетном периоде по сравнению с базисным возросла в среднем на 20% (Ip,= 1,20), а физический объем товарооборота в фиксированных ценах снизился на 5% (Iq = 0,95), то можно определить изменение объема товарооборота в фактических ценах: Ipq = Ip.Iq = 1,20 . 0,95 = 1,14 или 114%. Таким образом, при снижении физического объема товарооборота на 5%, товарооборот в фактических ценах в отчетном периоде по сравнению с базисным вырос на 14% вследствие роста цен на единицу товара в среднем на 20%. Аналогично можно найти взаимосвязь между индексами затрат на производство продукции, себестоимости и физического объема продукции: Izq = Iz. Iq Индекс изменения общего фонда оплаты труда в связи с изменением общей численности работающих Т и заработной платы f: IF= IT. If К числу взаимосвязанных индексов относятся и индексы переменного состава, индексы постоянного состава и индексы структурных сдвигов. В этой системе динамика среднего показателя (индекса переменного состава) выступает как произведение двух индексов: индекса среднего показателя в неизменной структуре (индекс постоянного состава) и индекса влияния изменения структуры явлений на динамику среднего показателя (индекс структурных сдвигов): Индексная система позволяет определить влияние отдельных факторов на формирование уровня результативного показателя, по двум известным значениям индексов найти значение третьего – неизвестное. Например, известно, что затраты на производство всей продукции в отчетном периоде по сравнению с базисным выросли на 15% ( Izq = 1,15) и одновременно уровень себестоимости единицы продукции снизился на 4% (Iz = 0,96), то можно определить, что физический объем продукции вырос на 20%: Рассмотренные системы являются двухфакторными (результативный признак связан с двумя факторами). Но общий признак может зависеть от трех. Четырех и более факторов, то есть связь может трех-, четырехфакторная и т.д. Поэтому общие индексы могут быть разложены также на три, четыре и более факторных индекса, объясняющих изменение результативного признака за счет влияния каждого фактора в отдельности. Обозначим факторные признаки a, b, c, тогда система взаимосвязанных индексов будет иметь следующий вид: Аналогично строится система взаимосвязанных индексов при четырехфакторной связи и т.д. Аналогично строится система взаимосвязанных индексов при большем количестве факторов - четырех и т.д. | |||||||||||||||||||
