Курс лекций. Теория статистики Пособие для студентов, обучающихся по дистанционной системе Введение Статистика
 Скачать 2.79 Mb.
|
|
Тема 9. Индексный метод
Индексы, их сущность. Индивидуальные индексы и их взаимосвязи Индексы являются наиболее распространенными в экономическом анализе показателями. Значительное число показателей, публикуемых в статистических сборниках, имеет форму индексов. Индексы характеризуют развитие национальной экономики в целом и отдельных её отраслей, анализируются результаты производственно-хозяйственной деятельности предприятий, исследуется роль отдельных факторов в формировании важнейших экономических показателей. Индексы используются для сопоставления экономических показателей между странами, мониторинге деловой активности, при оценке финансовых инструментов. Термин индекс происходит от латинского INDEX – указатель, показатель. Индекс представляет собой относительную величину, получаемую в результате сопоставления уровней сложных социально-экономических во времени, пространстве или по сравнению с любым эталоном (нормативом, планом, прогнозом и т.д.). Каждый индекс включает данные за два периода: отчетный (сравниваемый, текущий) и базисный, который используется как база сравнения. Данные отчетного периода обозначают подстрочным знаком 1, данные базисного – 0. Основным элементом индексного отношения является индексируемая величина, под которой понимается значение признака статистической совокупности, и изменение которой является предметом изучения, что отражается в названии индекса, например, индекс цен, индекс себестоимости, индекс товарооборота и др. Индексный метод имеет свою терминологию и символику. Каждая индексируемая величина имеет обозначение: q – количество (объем) какого-либо продукта в натуральном выражении (от латинского слова quantitas); p – цена единицы товара (от латинского слова pretium); z – себестоимость единицы продукции; t – затраты времени на производство единицы продукции (трудоемкость); w – выработка продукции в стоимостном выражении на одного работника или единицу времени; v – выработка продукции в натуральном выражении на одного работника или единицу времени; Т – общие затраты времени (T = tq) или численность работников; рq – общая стоимость произведенной продукции данного вида или общая стоимость проданных товаров данного вида (товарооборот, выручка); zq – затраты на производство всей продукции. Индексы, характеризующие изменение значений только одного признака называются индивидуальными, обозначаются i и снабжаются подстрочным знаком индексируемого показателя: iq – индивидуальный индекс объема произведенной продукции отдельного вида или количества (объема) проданного товара данного вида; ip – индивидуальный индекс цен и т.д. Индивидуальные индексы рассчитывают как отношение двух индексируемых величин. ip = p1 / p0 – индивидуальный индекс цен, где p1 , p0 - цены единицы продукции в текущем (отчетном) и базисном периодах. iq = q1 / q0 - индивидуальный индекс физического объема продукции. Например, цены на акции Роснефти в 1 квартале 2007 года по сравнению с 4 кварталом 2006 года. С аналитической точки зрения индивидуальные индексы аналогичны темпам роста и характеризуют изменения индексируемой величины в текущем периоде по сравнению с базисным. Значения индексов выражают в коэффициентах и процентах. Сводные (общие) индексы - отражают изменение всех элементов сложного явления. При этом под сложным явлением понимают такую статистическую совокупность, отдельные элементы которой непосредственно не подлежат суммированию (физический объем продукции, включающей разноименные изделия, товары, цены на разные группы продуктов и т.д.). Так, например, индекс промышленной продукции дает сводную характеристику изменении выпуска всех видов промышленной продукции в отчетном периоде по отношению к базисному. Общий индекс обозначается буквой I и также сопровождается подстрочным знаком индексируемого показателя. Например, Ip – общий индекс цен, Iz – общий индекс себестоимости Если индексы охватывают не все элементы сложного явления, а лишь часть, то их называют групповыми или субиндексами. Например, индексы продукции по отдельным отраслям промышленности. Правила построения и использования общих и групповых индексов представляют собой особый прием статистического исследования, называемый индексным методом. В зависимости от содержания и характера индексируемой величины различают индексы количественных (например, индекс физического объема продукции) и качественных показателей (например, индекс цен). В зависимости от выбора уровней сравнения возможны два способа расчета индексов – цепной и базисный. Цепные индексы получают путем сопоставления текущих уровней с предшествующим. Таким образом, база сравнения непрерывно меняется. Базисные индексы получают путем сопоставления с уровнем периода, принятого за базу сравнения. По методологии расчета различают агрегатные индексы и средние из индивидуальных. Агрегатные индексы. Проблема соизмерения индексируемых величин Агрегатные индексы наряду с индексируемым признаком (признак динамика, которого изучается) содержат и признак-вес, который позволяет соизмерить и обобщить разнородные элементы совокупности. Индексируемый признак при построении агрегатного индекса меняется: отчетный период сравнивается с базисным. Признак-вес берется на неизменном фиксированном уровне. Если ставится вопрос: как изменилось количество проданных товаров в целом (акций, векселей, ткани, обуви, швейных изделий и т.д.) в отчетном периоде по сравнения с базисным, то необходимо предварительно определить, сколько всего продано товаров в отчетном периоде и сколько в базисном? Общее количество проданных товаров подсчитать в натуральном выражении нельзя, т.к. различные товары в натуральном выражении несоизмеримы. Но соизмерить товары можно либо при помощи затрат труда на производство единицы продукции (t), либо при помощи себестоимости единицы продукции (с), либо при помощи цены (р). Так, стоимость продукции представляет собой произведение количества продукции в натуральном выражении q на цену единицы продукции р. Отношение стоимости продукции отчетного периода  к стоимости продукции базисного периода  представляет собой общий индекс стоимости продукции или товарооборота: (1)Этот индекс является простым и показывает во сколько раз возросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным, или сколько процентов составляет рост (снижение) стоимости продукции. Если индекс стоимости будет больше 1, то стоимость продукции в отчетном периоде выросла, если меньше 1, то - снизилась. Разность числителя и знаменателя формулы (1)  показывает на сколько денежных единиц изменилась стоимость продукции в текущем периоде по сравнению с базисным. Показатель общей стоимости изменяется под влиянием двух факторов: 1) цен и 2) количества. Для того, чтобы сравнением общих стоимостей показать изменение только количества необходимо оценить продукцию (или товары) отчетного и базисного периодов по ценам какого-либо одного периода, например, базисного. Тогда формула агрегатного индекса физического объема (количества) продукции, будет выглядеть так: Iq =  (2)Этот индекс показывает во сколько раз изменился физический объем продукции или сколько % составляет его рост (снижение) по сравнению с базисным. В числителе индекса – условная стоимость произведенной в текущем периоде продукции в ценах базисного периода, а в знаменателе – фактическая стоимость товаров, произведенных в базисном периоде. Такой вариант построения агрегатного индекса был предложен Э.Ласпейресом в 1864 году. «Агрегатным» он называется потому, что его числитель и знаменатель представляют набор «агрегат» (от латинского aggregatus – складываемый, суммируемый) непосредственно несоизмеримых и не поддающихся суммированию элементов – сумму произведений двух величин, одна из которых меняется (суммируется), а другая – остается неизменной в числителе и знаменателе (вес индекса). Вес индекса служит для соизмерения индексируемых величин. Разность числителя и знаменателя формулы (2)  показывает на сколько денежных единиц изменилась стоимость продукции в результате роста (уменьшения) её объема. Если поставить задачу характеристики изменения физического объема выпуска продукции, то правомерно в качестве соизмерителя использовать и цены отчетного периода, тогда индекс физического объема продукции будет записан так:  (3)Агрегатный индекс с весами отчетного периода был предложен в 1874 году Г.Пааше. Таблица 1. Объем выпуска продукции предприятия по видам
Индекс динамики объема производства оборудования составляет 95,24%, что означает снижение его выпуска на 4,76% (  ). В динамике же выпуска литья наблюдается противоположная тенденция: выпуск литья возрос на 4,35% ( ). Общее изменение выпуска продукции предприятия может быть получено на основе определения агрегатной формы индекса физического объема продукции. Проведем расчет агрегатных индексов физического объема продукции в двух вариантах:- в качестве соизмерителей используются цены базисного периода; - соизмерителями разнородной продукции предприятия являются текущие цены (цены отчетного периода). Стоимостные показатели выпуска продукции, необходимые для расчета индексов, приведены в таблице 2. Таблица 2. Расчет стоимости выпуска продукции
Агрегатный индекс динамики физического объема продукции, рассчитанный по формуле Ласпейреса, составит 0,9879:  , - агрегатный индекс физического объема продукции, рассчитанный по формуле Ласпейреса.Таким образом, физический объем выпуска продукции предприятия в ценах базисного периода снизился на 98,79% - 100% = -1,21%. В абсолютном выражении это составило:  тыс.руб. Величина агрегатного индекса физического объема, рассчитанного по формуле Пааше  , равна 0,98894: , или 98,894%,то есть физический объем выпуска продукции предприятия, рассчитанный в текущих ценах, уменьшился на 98,894% - 100% = -1,106%. В абсолютном выражении это снижение составило:  тыс.руб.Если сопоставить величины двух индексов и , то, несмотря на некоторые различия в величине, они отражают одну и ту же тенденцию – снижение физического объема выпуска продукции предприятия.Можно обобщить результаты разновзвешенных индексов физического объема, рассчитав среднюю геометрическую из них  (4)Этот индекс называется индексом Фишера.  или 98,81%Какой бы вариант построения индекса не был выбран – индекс Ласпейреса или индекс Пааше, его необходимо использовать постоянно, иначе сравнение значений индекса за различные периоды времени будет бессмысленным. Агрегатные индексы Ласпереса и Паше применяются и для построения индексов цен, соизмеряющих изменения цен в отчетном и базисном периодах при фиксированных уровнях объема. Индекс цен по формуле Ласпейреса с базисными весами примет вид:  (5).Индекс цен по формуле Паше с весами отчетного периода примет вид:  (6)Индекс Фишера:  (7)Проведем расчет индексов цен для нашего примера. Индекс Ласпейреса:  То есть, если бы структура производства базисного периода сохранилась в отчетном, то рост цен составил бы 112,12% или, формулируя иначе, цены выросли бы на 12,12%. В абсолютном выражении условная экономия на ценах составила:  тыс.руб.Применение индекса цен Ласпейреса ограничено особыми условиями исследования. Например, при прогнозировании объемов товарооборота, в связи с намечаемыми изменениями цен на товары в предстоящем периоде). Индекс Пааше:  Уровень цен в отчетном периоде по сравнению с базисным по продукции, произведенной в базисном периоде, возрос на 11,23%. В абсолютных значениях сумма дохода, полученная от роста цен в отчетном периоде составила:  тыс.руб.Индекс Фишера:  или 112,17% Рассчитаем сводный индекс производства в фактических ценах:  Стоимостной объем производства (товарооборота) в фактических ценах возрос на 11,09%. В денежном выражении рост производства составил:  тыс.руб.Значение индекса отражает одновременное влияние обоих факторов – изменение количества (объема) продукции и изменение уровня цен.Индексы товарооборота, физического объема по формуле Ласпейреса и индекс цен по формуле Пааше связаны между собой:  Или  = -3125+31200=28075 тыс.руб.Таким образом, рост цен на производимую продукцию перекрыл убытки от сокращения выпуска дорогостоящего оборудования и предприятие в среднем увеличило выпуск на 10,87% или 28075 тыс.руб. 9.3. Средний арифметический и средний гармонический индексы, тождественные агрегатному Наряду с агрегатными общие индексы могут быть построены как средние взвешенные из индивидуальных, тождественных агрегатным. Предположим, что необходимо рассчитать агрегатный индекс цен по формуле Паше (формула 6 с отчетными весами:  ), но неизвестны отдельные значения p1 и q1, а дано их произведение p1q1 (товарооборот текущего периода) и известны индивидуальные индексы цен  . Как это сделать? Из формулы 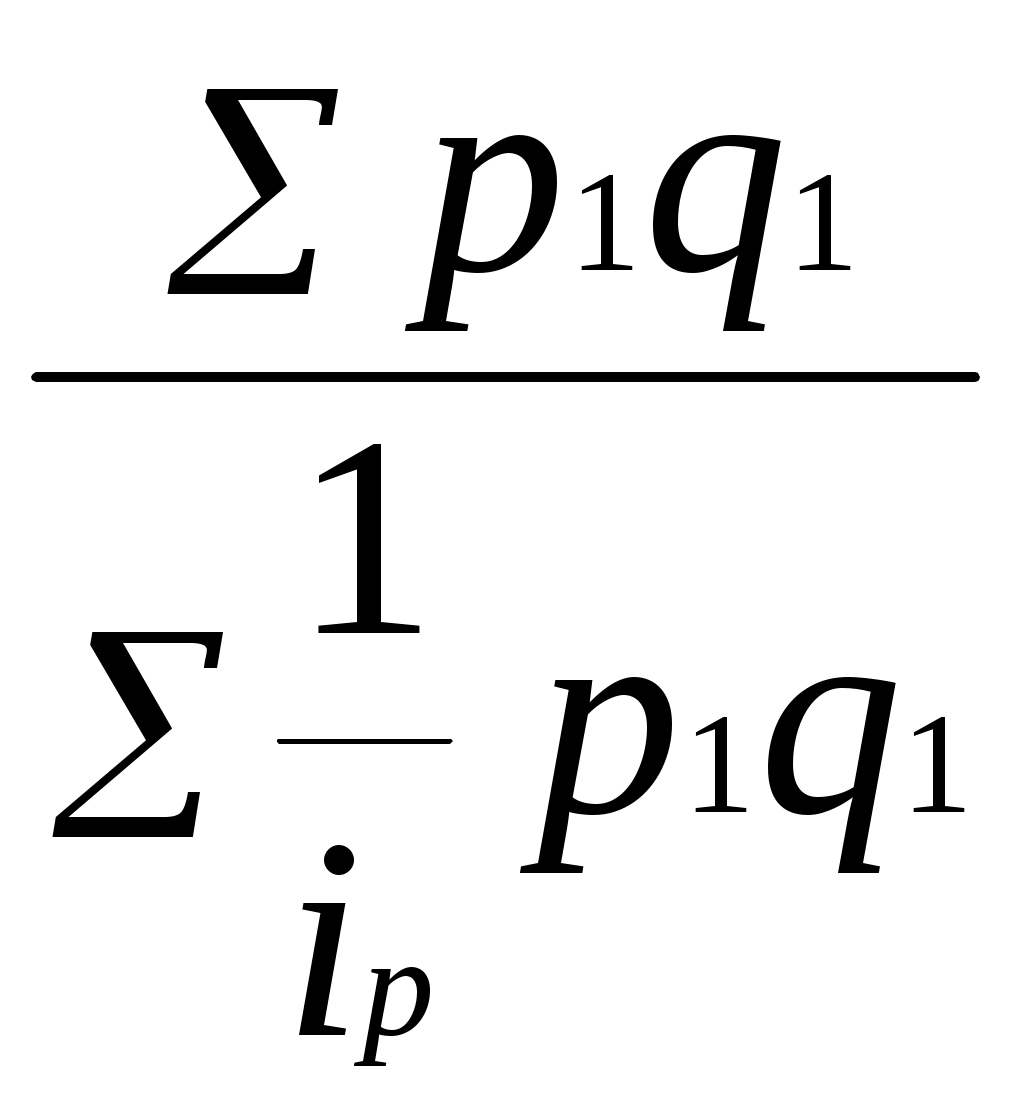определяем  , подставляем его в знаменатель агрегатной формулы:   Ip =  Ip =  (8)В результате получили средний гармонический индекс цен, тождественный агрегатному индексу Пааше. Весами индивидуальных индексов в этом индексе служит стоимость отдельных видов продукции отчетного периода в ценах этого же периода p1q1. Предположим нам необходимо построить агрегатный индекс цен Ласпейреса ( формула 5 с базисными весами:  ). Нам не известны значения  и  , но известно их произведение  , а так же индивидуальные индексы цен . Из индивидуального индекса цен выразим цены отчетного периода  и подставим в числитель агрегатного индекса цен  , (9)В результате получили средний арифметический индекс цен тождественный агрегатному индексу цен Ласпейреса. Весами осредняемых индивидуальных индексов  в этом индексе служит объем товарооборота в базисном периоде  .Агрегатные индексы физического объема можно выразить так же через индивидуальные индексы: тождественный агрегатному индексу Паше как средней гармонический и тождественный агрегатному индексу Ласпейреса как средний арифметический. Например, если неизвестны значения 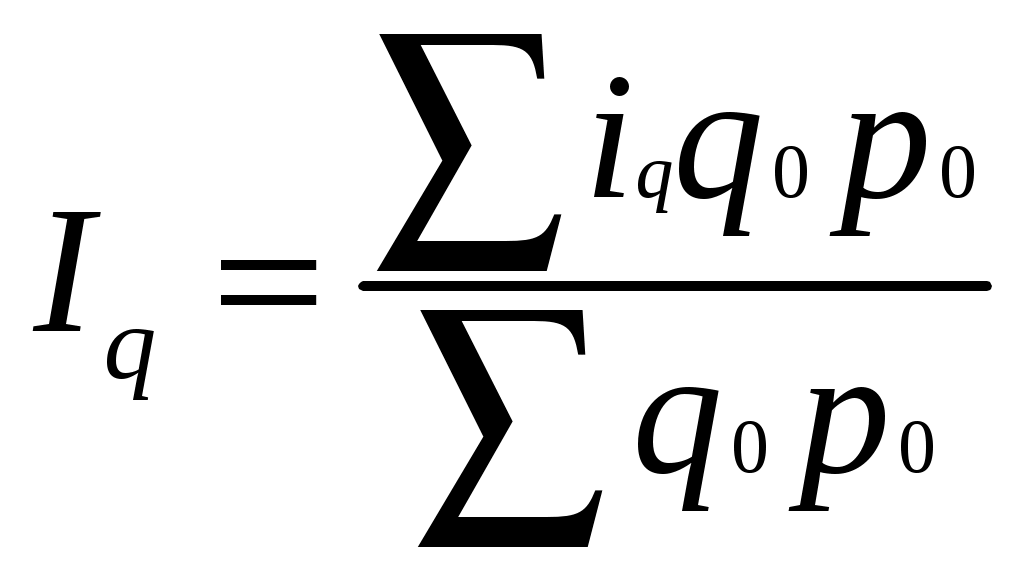и , но известно их произведение , а так же индивидуальные индексы физического объема  . Из индивидуального индекса физического объема выразим объемы отчетного периода iq =    - подставляем в агрегатный индекс   (10)В результате получили средний арифметический индекс физического объема, тождественный агрегатному индексу Ласпейреса. При выборе весов следует иметь в виду, что средний индекс должен быть тождественен агрегатному, который является основной формой индекса. Учитывая, что соотношение  характеризует долю данного вида продукции в общей стоимости продукции базисного периода  , средний арифметический индекс физического объема (10) будет иметь вид: Например, воспользуемся данными графы 6 таблицы 1 и графы 2 таблицы 2 для расчета среднего арифметического индекса физического объема продукции:  Получим такой же результат, как и при расчете агрегатного индекса физического объема по формуле Ласпейреса. Допустим, что имеются данные о динамике объема выпуска каждого вида продукции 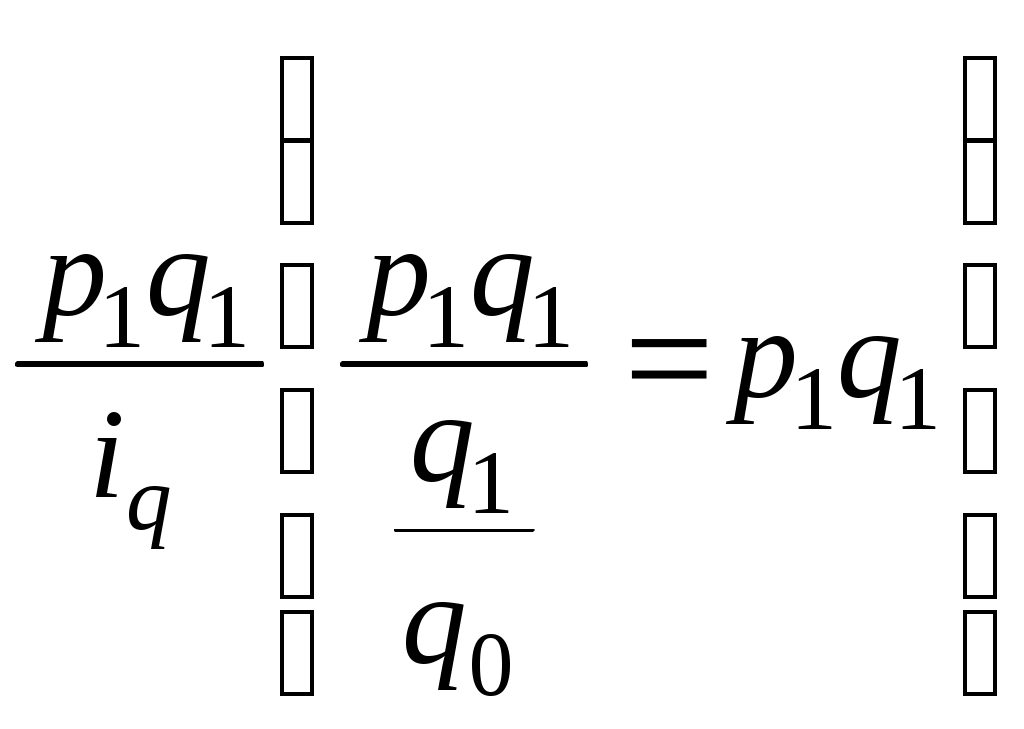 и стоимости каждого вида продукции в отчетном периоде  , тогда индекс физического объема можно получить путем суммирования величин , а знаменатель – путем деления фактической стоимости каждого вида продукции на соответствующий индивидуальный индекс физического объема продукции, то есть путем деления: ,тогда  (11).Таким образом, в этом случае расчет выполняется по формуле среднего взвешенного гармонического индекса физического объема тождественного агрегатному индексу Пааше. Например, используем графы 6 таблицы 1 и графы 3 таблицы 2:  .Получен такой же результат, как и при расчете агрегатного индекса по формуле Пааше. Из сказанного следует, что применение той или иной формулы индекса физического объема (агрегатного, среднего арифметического или среднего гармонического) зависит от имеющейся в нашем распоряжении информации. . Рассмотрение методологии исчисления индексов и их применения в экономическом анализе сказать, что важной особенностью общих индексов, построение и расчет которых составляет суть индексного метода, является то, что они обладают синтетическими и аналитическими свойствами. Синтетические свойства общих индексов состоят в том, что они выражают относительные изменения сложных (разнотоварных) явлений, отдельные части и элементы которых непосредственно несоизмеримы. Аналитические свойства общих индексов говорят о том, что посредством индексного метода определяется влияние факторов на изменение изучаемого показателя. Индексный метод анализа динамики среднего уровня: индексы переменного, постоянного состава и структурных сдвигов Индексным методом можно воспользоваться для характеристики динамики средних показателей уровней. Динамика среднего уровня (среднего показателя находится под влиянием двух факторов: 1) изменение осредняемой величины, 2) изменение структуры явления или удельного веса численности отдельных групп в общем итоге (в общей численности). Например, средняя заработная плата работников предприятия может изменяться в результате изменения ставок заработной платы у отдельных категорий работников и в результате изменения удельного веса работников с различным уровнем оплаты труда. Очень важно отметить следующее: при изучении динамики среднего показателя ставится задача показать роль каждого фактора в динамике этого показателя. т.е. измерить степень влияния в отдельности каждого фактора. С этой целью и строится система взаимосвязанных индексов: переменного состава, постоянного (фиксированного) состава (в постоянной структуре) и структурных сдвигов. Индексы, исчисляемые путем сопоставления средних показателей, называются индексами переменного состава. Индексы переменного состава находятся под влиянием двух факторов, о которых говорилось выше. В индексе постоянного (фиксированного) состава элиминируется, т.е. устраняется влияние второго структурного фактора и исчисляются они, таким образом, в постоянной структуре. Индекс структурных сдвигов (или индекс структуры) позволяет измерить степень (меру) влияния структурных сдвигов. Исчисляются эти индексы по следующим формулам: Индексы переменного состава:  (11)Зная, что  , индекс можно представить в таком виде: Индексы постоянного (фиксированного) состава: 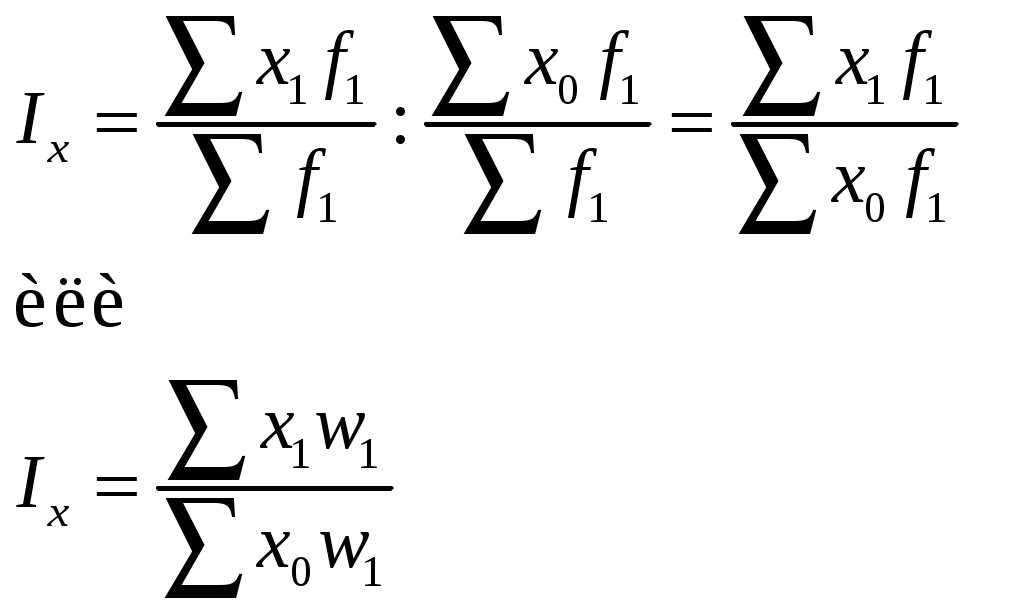 (12)Индексы структурных сдвигов:  (13)Между разобранными индексами существует следующая взаимосвязь:  Следовательно,  Индексы позволяют оценить динамику показателей, характеризующих разнородные в качественном отношении совокупности, как правило, товарные группы. Однако, даже если рассматриваемая совокупность однородна (товар или вид продукции одного вида) на величине результативного показателя будет отражаться влияние структурных изменений, например, изменений в структуре производства или реализации данного товара по территориям. Рассмотрим случай, когда один товар или вид продукции реализуется или производится в нескольких местах | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
