матан. Теория вероятностей кажется не совсем обычной математической дисциплиной, так как имеет дело с особой категорией со случайностью. Роль случая в нашей жизни, как известно, весьма значительна
 Скачать 3.15 Mb.
|
|
Пример 4.3. Непрерывная случайная величина Х задана плотностью распределения  в интерв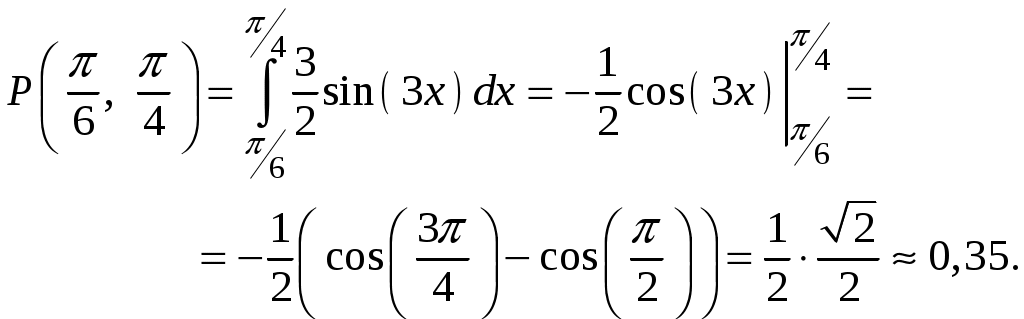але  ; вне этого интервала  . Найти вероятность того, что Х примет значение, принадлежащее интервалу  Решение.  Пример 4.4. Задана плотность распределения непрерывной случайной величины Х: 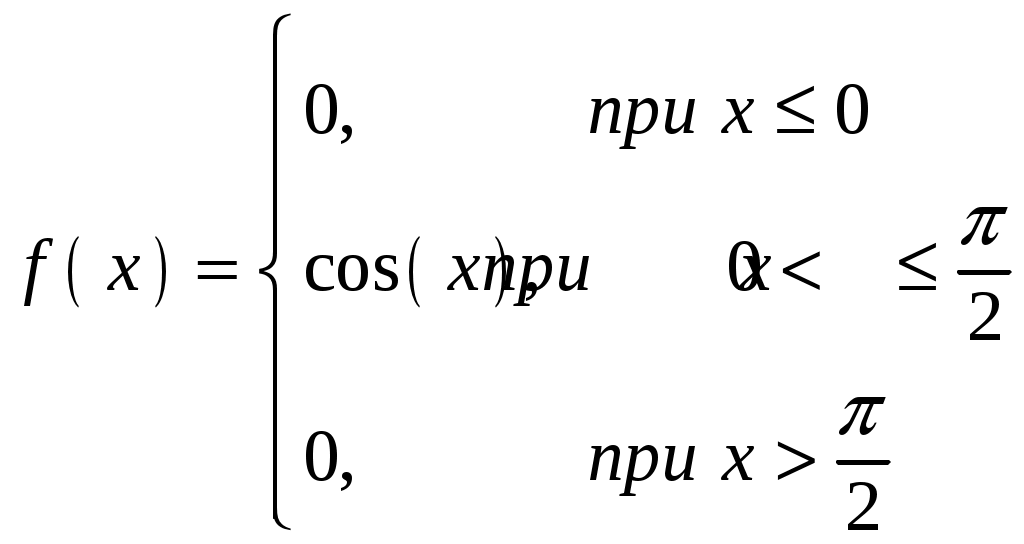 Найти функцию распределения  .Р  ешение.Используем формулу 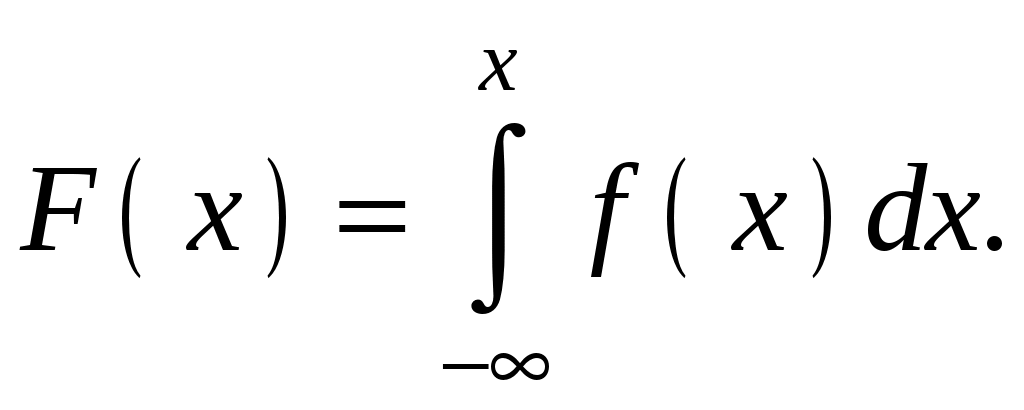 При 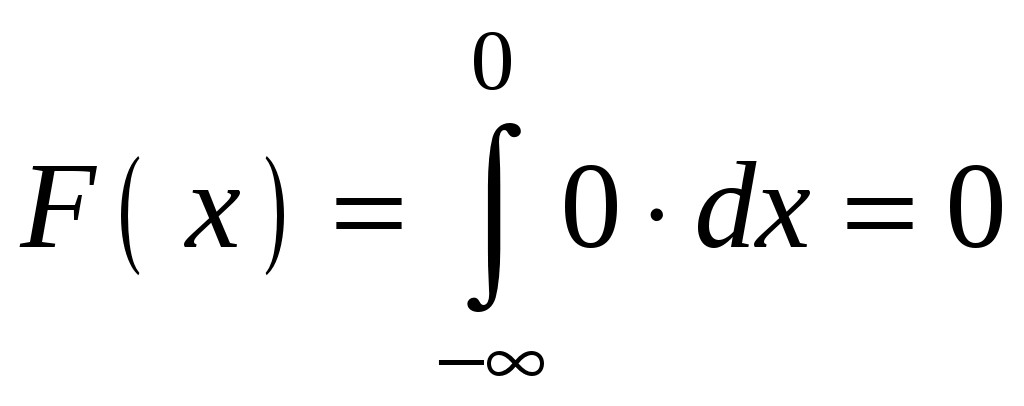 ;  .При 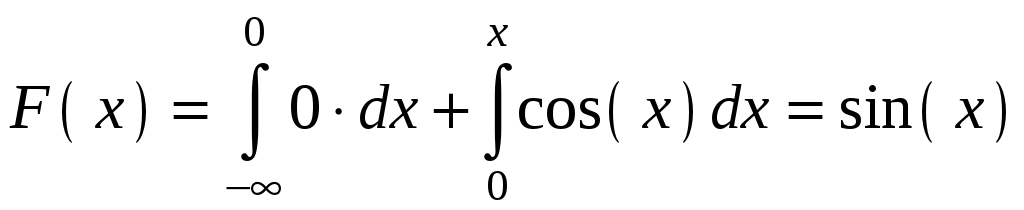 :  .При 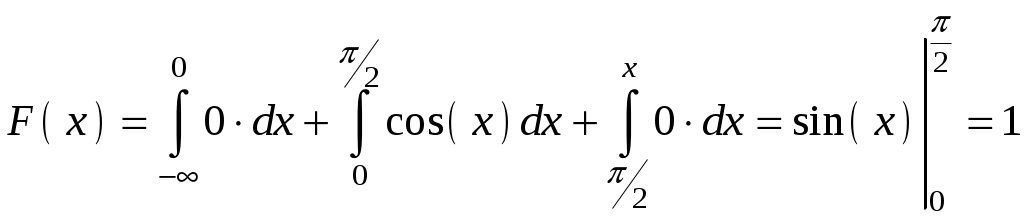 ;  .Тогда: 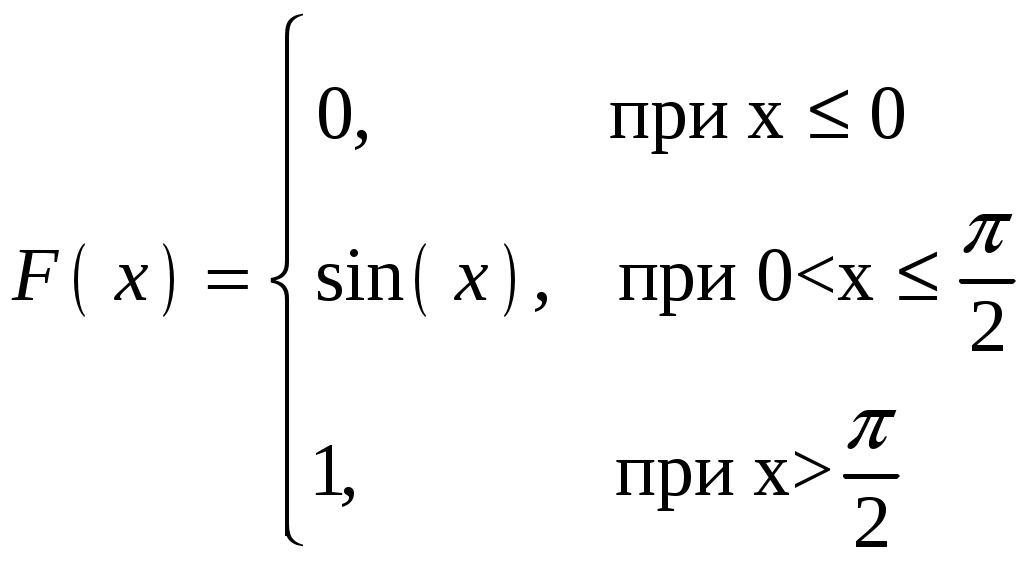 Графики 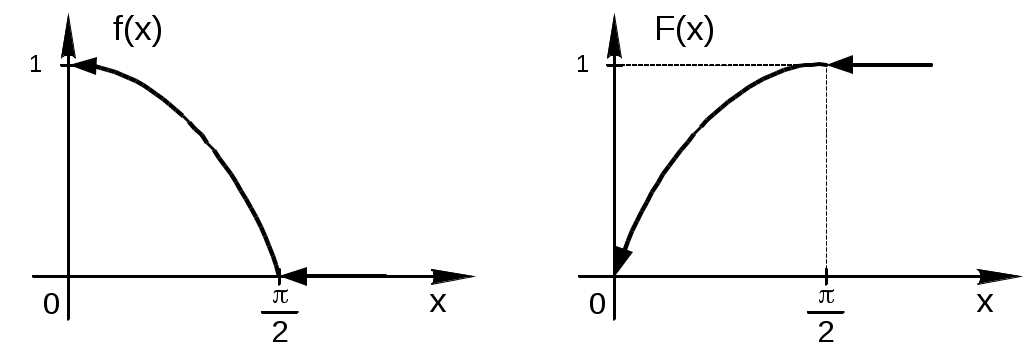 и : Пример 4.5. Случайная величина Х задана на всей оси Ох функцией распределения  .Найти возможное значение  , удовлетворяющее условию: с вероятностью  случайная величина Х в результате испытания примет значение, большее  .Решение. События  и  – противоположные, поэтому .Следовательно,  .Так как  , то  .По определению функции распределения,   .Следовательно,  или  .Отсюда  , или  .Пример 4.6. Дискретная случайная величина Х задана законом распределения
|