матан. Теория вероятностей кажется не совсем обычной математической дисциплиной, так как имеет дело с особой категорией со случайностью. Роль случая в нашей жизни, как известно, весьма значительна

• Название: Теория вероятностей кажется не совсем обычной математической дисциплиной, так как имеет дело с особой категорией со случайностью. Роль случая в нашей жизни, как известно, весьма значительна
• Анкор: матан
• Дата: 28.03.2023
• Размер: 3.15 Mb.
• Имя файла: Matematika3_TEKST.doc
• Тип: Документы; #1021296
• страница: 5 из 8

Глава 3. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

1. 
   Основные понятия
   

Одним из основных понятий теории вероятностей является понятие случайной величины.

Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем заранее не известно как именно.

Случайные величины обозначаются большими буквами латинского алфавита: Х, Y, Z, …, а их возможные значения – малыми буквами: x, y, z,….

Различают дискретные и непрерывные случайные величины.

Величина Х называется дискретной случайной величиной, если множество ее возможных значений представляет собой конечную или бесконечную последовательность чисел: х₁, х₂,… и если каждое событие имеет определенную вероятность , то пишут .

Другими словами, возможные значения дискретной случайной величины можно перенумеровать. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (в последнем случае множество всех возможных значений называют счетным).

Например. Число попаданий при трех выстрелах. Возможные значения случайной величины: 0, 1, 2, 3.

Оценка на экзамене. Возможные значения случайной величины: 2, 3, 4, 5.

Случайные величины, возможные значения которых непрерывно заполняют промежуток, называются непрерывными случайными величинами.

Например. Время безотказной работы некоторого двигателя. Случайная величина может принимать любые значения, не отделенные друг от друга.

Случайная величина будет описана полностью, если установлена связь между возможными ее значениями и вероятностью их появления.

Всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями, называется законом распределения случайной величины.

Закон распределения задается либо формулой, выражающей вероятность , как функцию от , либо таблицей, в которой перечисляются все возможные значения случайной величины и их вероятности.

В частности, для дискретных случайных величин закон распределения задается таблицей, в которой перечисляются все возможные значения случайной величины и их вероятности, а для непрерывных случайных величин – функцией от .

3.2. Функция распределения вероятностей случайной величины
Функция распределения вероятностей случайной величины (или просто «функция распределения») – универсальная характеристика случайной величины. Она существует для всех случайных величин – и непрерывных, и дискретных.

Функцией распределения вероятностей случайной величины Х называется вероятность того, что случайная величина Х в результате испытания примет значение меньше х, т.е.

.

Часто вместо термина «функция распределения» используют термин «интегральная функция распределения».
Свойства функции распределения
Функция распределения обладает следующими свойствами:

Свойство 1. Значения функции распределения принадлежат отрезку [0;1]:

.

Свойство 2. Функция распределения есть неубывающая функция:

, если .

Следствие 1. Вероятность того, что случайная величина X примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале:

.

Следствие 2. Вероятность того, что непрерывная случайная величина X примет одно определенное значение, например , равна нулю:

.

Свойство 3. Если все возможные значения случайной величины X принадлежат интервалу (a, b), то



Свойство 3. . Это следует из того, что есть невозможное событие.

. Это следует из того, что есть достоверное событие.

Следствие. Справедливы следующие предельные соотношения:

.

Свойство 4. Функция распределения непрерывна слева:

.

График функции распределения есть график неубывающей функции, значения которой меняются от 0 до 1.

Для непрерывной случайной величины – это непрерывная линия.

Для дискретной случайной величины – это разрывная случайная кривая, скачки которой происходят в точках, соответствующих возможным значениям случайной величины.

3. 
   Дискретные случайные величины
   

Рассмотрим дискретную случайную величину Х с возможными значениями х₁, х₂,…, х_n. Каждое из этих значений возможно, но не достоверно и величина Х может принять каждое из них с некоторой вероятностью. В результате опыта величина Х примет одно из этих значений, т.е. 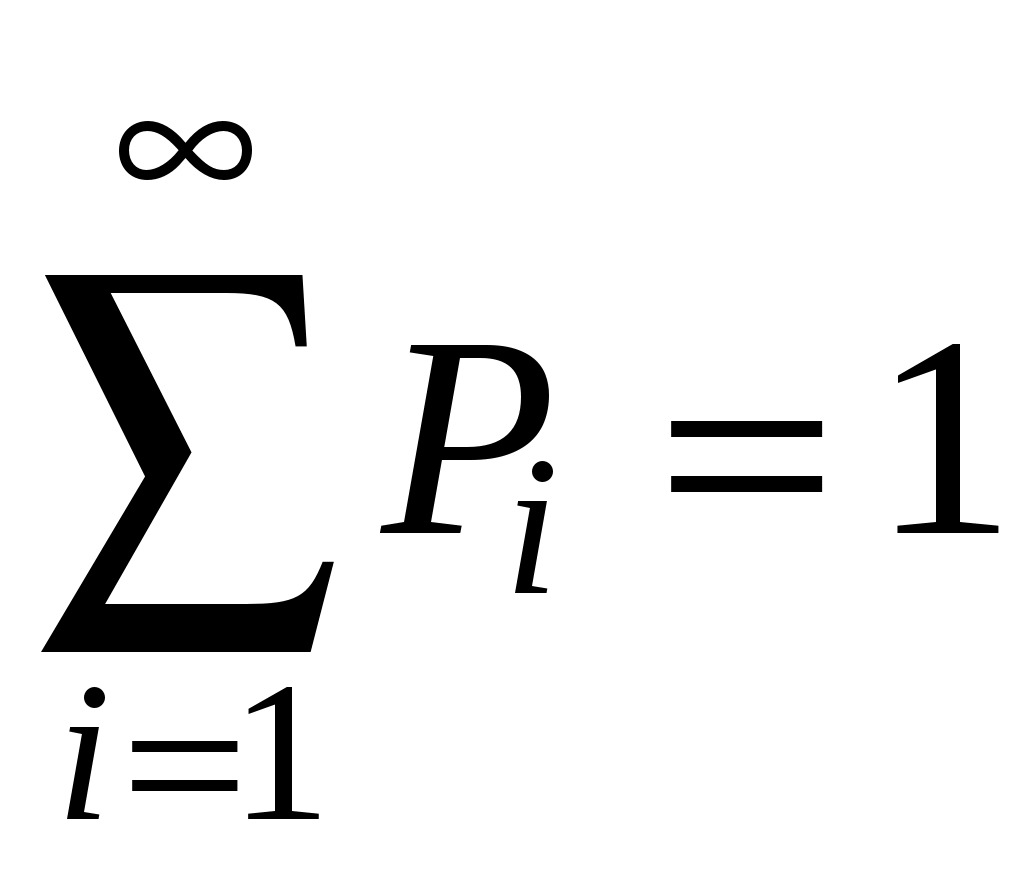, , …, образуют полную группу несовместных событий: , , …, . Так как события образуют полную группу несовместных событий, то

.

Это условие называют условием нормировки.

Если множество возможных значений величины Х бесконечно то ряд: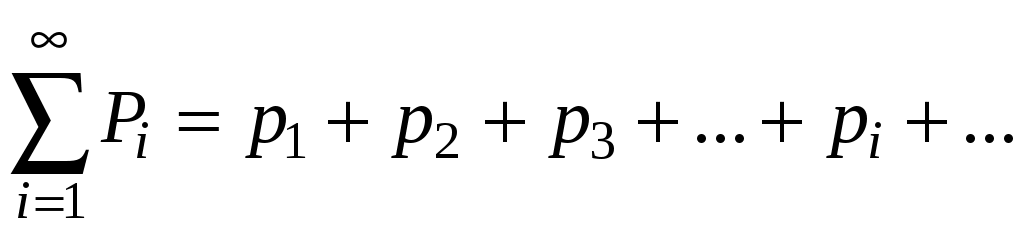



должен быть сходящимся и его сумма должна быть равна единице.

Законом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей. Закон распределения дискретной случайной величины X может быть задан в виде таблицы.

Таблица, в которой перечислены все возможные значения случайной еличиины и соответствующие им вероятности, называется рядом распределения дискретной случайной величины:



, где i=1;2;...;n;…

Закон распределения дискретной случайной величины X может быть также задан аналитически (в виде формулы):



или с помощью функции распределения (см. предыдущий параграф).

Закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки с координатами: (x₁; p₁), (x₂; p₂), … , (x_n; p_n), где x_i – возможные значенияX, p_i – соответствующие вероятности, и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

Многоугольник распределения, как и ряд распределения, полностью характеризует случайную величину. Он является одной из форм его закона распределения.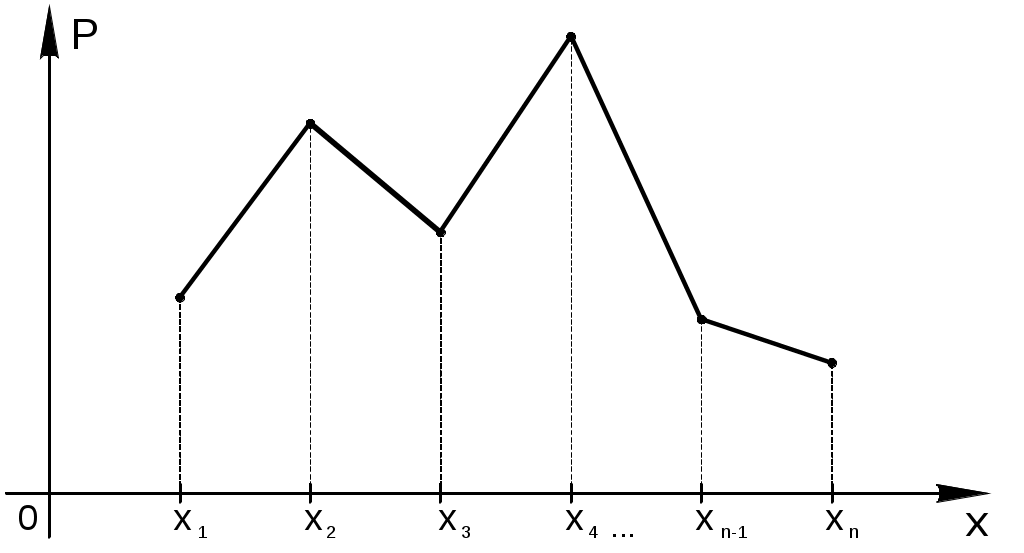

3. 
   Числовые характеристики дискретной случайной величины
   

Случайные величины полностью характеризуются законом распределения. Однако во многих задачах нет необходимости так полно характеризовать случайную величину. Часто бывает достаточно указать только параметры, характеризующие случайную величину, какое-то среднее значение, около которого группируются возможные числовые значения случайной величины; или какое-либо число, характеризующее степень разбросанности этих значений относительно среднего или центра. Такие характеристики, выражающие в сжатой форме наиболее существенные особенности распределения, называются числовыми характеристиками случайной величины.

К основным числовым характеристикам любой случайной величины (т.е. дискретной и непрерывной) относятся:

• 
  математическое ожидание;
  
• 
  дисперсия;
  
• 
  среднее квадратическое отклонение.
  

Наиболее часто в теории вероятностей используют математическое ожидание и дисперсия.

Математическим ожиданием (или средним значением) дискретной случайной величины называется сумма произведений всех ее возможных значений на их вероятности:

.

Если дискретная случайная величина имеет n возможных значений, то

.

Иногда математическое ожидание случайной величины обозначают .

Математическое ожидание называется центром рассеивания распределения вероятностей случайной величины.
Свойства математического ожидания
Математическое ожидание обладает следующими свойствами.

Свойство 1. Математическое ожидание постоянной величины равно самой постоянной:

.

Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:

.

Свойство 3. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:



Свойство 4. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:



Зная лишь математическое ожидание случайной величины, еще нельзя судить о распределении значений случайной величины около математического ожидания. Для оценки рассеивания возможных значений случайной величины вокруг ее математического ожидания введена другая числовая характеристика, называемая дисперсией.

Дисперсией (или рассеиванием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

.

Данное определение справедливо и для дискретных и для непрерывных случайных величин.

Исходя из определения, можно записать дисперсию для дискретной величины: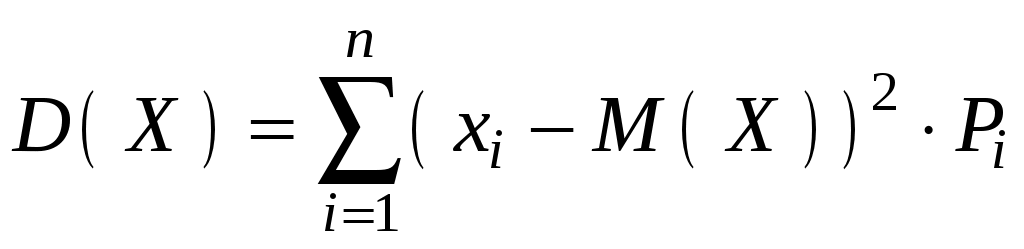

.

Дисперсию удобно вычислять по формуле:


Свойства дисперсии
Дисперсия обладает следующими свойствами.

Свойство 1. Дисперсия постоянной равна нулю:



Свойство 2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:

.

Свойство 3. Дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых:



Дисперсия имеет размерность квадрата случайной величины. Для наглядности удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины.

Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:

.

Данное определение справедливо и для дискретных и для непрерывных случайных величин.

Практически не встречаются такие значения случайной величины, отклонения которых от ее математического ожидания во много раз больше чем среднее квадратичное отклонение.
Свойства среднего квадратического отклонения
Свойство 1. Среднее квадратическое отклонение постоянной величины равна нулю:

.

Свойство 2. Постоянный множитель по абсолютной величине можно вынести за знак среднего квадратического отклонения:

.

Свойство 3. Среднее квадратическое отклонение суммы независимых случайных величин равно:

.

3. 
   Основные распределения дискретной случайной величины
   

Закон распределения случайных величин считается заданным если:

1. 
   указано множество возможных значений случайных величин;
   
2. 
   указан способ количественного определения вероятностей попадания случайных величин в произвольную область этого множества.
   

Законы распределения вероятностей определяются для функций от известных случайных величин: дискретных, непрерывных и смешанных.

Как было изложено ранее, для дискретных случайных величин закон распределения вероятностей задается в виде ряда, многоугольника, функций распределения.

Для непрерывных случайных величин закон распределения вероятностей задается в виде функции распределения (интегральной функции распределения) и плотности распределения (плотности вероятности, дифференциальной функции распределения).

Рассмотрим основные законы распределения дискретной случайной величины.

Биномиальное распределение
Биномиальным называют закон распределения дискретной случайной величины Х – числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна p; вероятность возможного значения X=m (числа m появлений события) вычисляют по формуле Бернулли:
_.

Математическое ожидание биномиального распределения равно произведению числа испытаний на вероятность появления события в одном испытании:



Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:



Распределение Пуассона
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равно р. Для определения вероятности появления события m раз в этих испытаниях используют формулу Бернулли. Если же n велико, то формула Бернулли неприменима.

При большом n и малом р используют асимптотическую формулу Пуассона, которая получается из формулы Бернулли при .

Распределение Пуассона имеет вид:

,

где (среднее число появлений события в n испытаниях),  называется интенсивностью потока.

Математическое ожидание и дисперсия распределения Пуассона равны a.


3.6. Примеры решения задач к главе 3
Пример 3.1. Дискретная случайная величина X задана законом распределения:

Х	1	3	6	8
Р	0,2	0,1	0,4	0,3

Построить многоугольник распределения.

Решение. Построим прямоугольную систему координат, причем по оси абсцисс будем откладывать возможные значения x_i, а по оси ординат – соответствующие вероятности p_i.

Построим точки M₁ (1; 0,2), М₂(3; 0,1), M₃(6;0,4) и M₄(8; 0,3). Соединив эти точки отрезками прямых, получим искомый многоугольник распределения: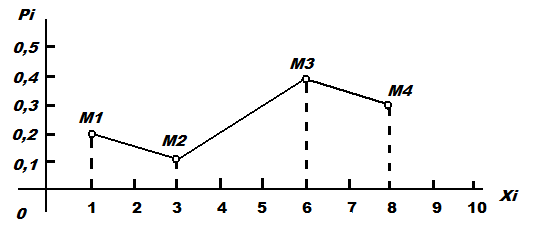



Пример 3.2. По мишени произведен один выстрел. Вероятность попадания в мишень равна 0,4. Построить ряд и многоугольник распределения числа попаданий.

Решение. Случайная величина Х – число попаданий в мишень, имеет два возможных значения: 0 и 1 с вероятностями 0,6 и 0,4.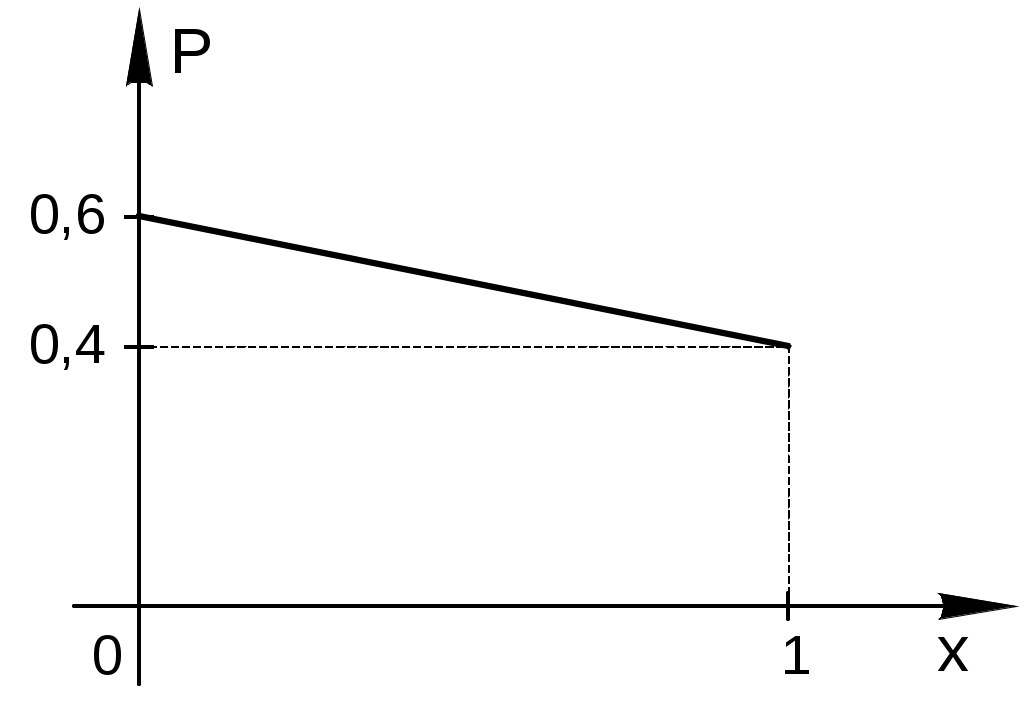

Х	0	1
Р	0,6	0,4

Пример 3.3. Построить график функции распределения случайной величины Х, заданной рядом распределения:

Х	0	1	2	3
Р	0,064	0,096	0,24	0,6

Решение. Составим функцию распределения .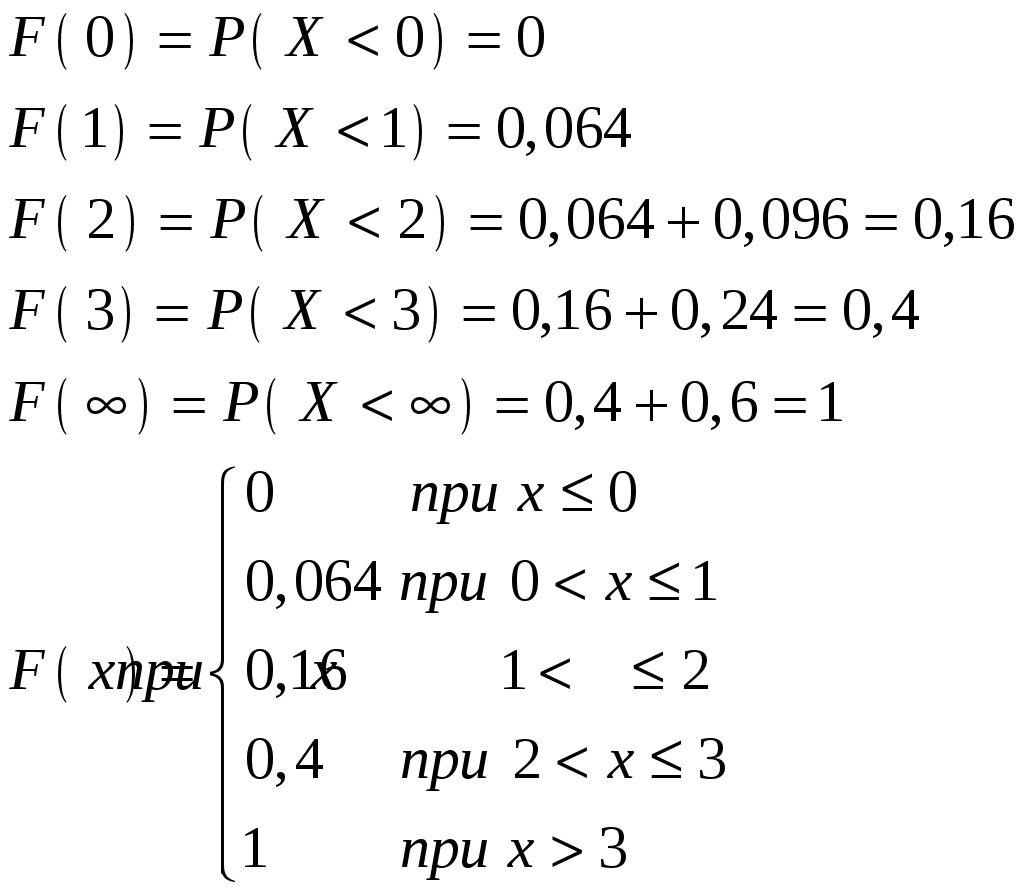



Построим график .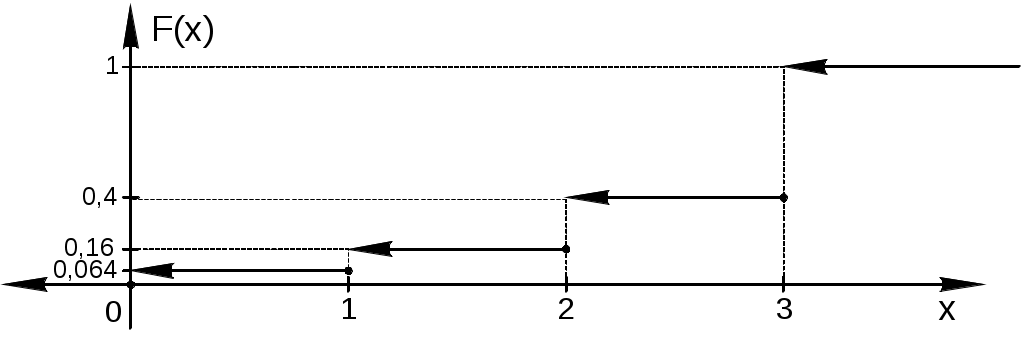



Вычислим .
Пример 3.4. Найти математическое ожидание дискретной случайной величины X, заданной законом распределения:

	-4	6	10
	0,2	0,3	0,5

Решение. Математическое ожидание равно сумме произведений всех возможных значений X на их вероятности:



Пример 3.5. Вероятность попадания в цель при одном выстреле Р=0,4. Определить математическое ожидание числа попаданий при трех выстрелах.

Решение. Возможное значение случайной величины – числа попаданий в цель – 0, 1, 2, 3.

Вероятность этих значений: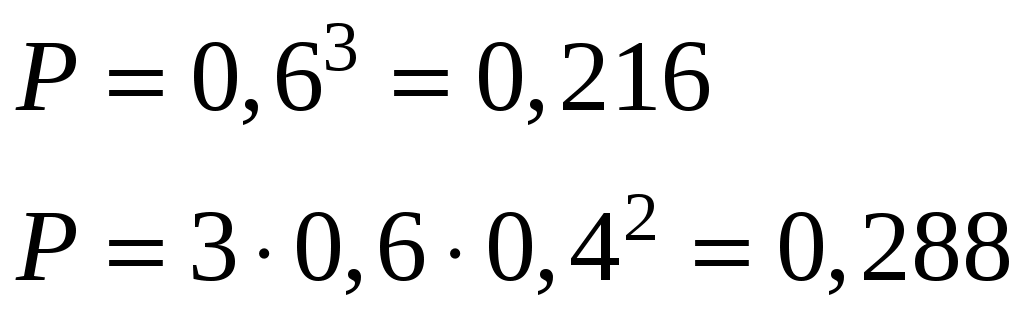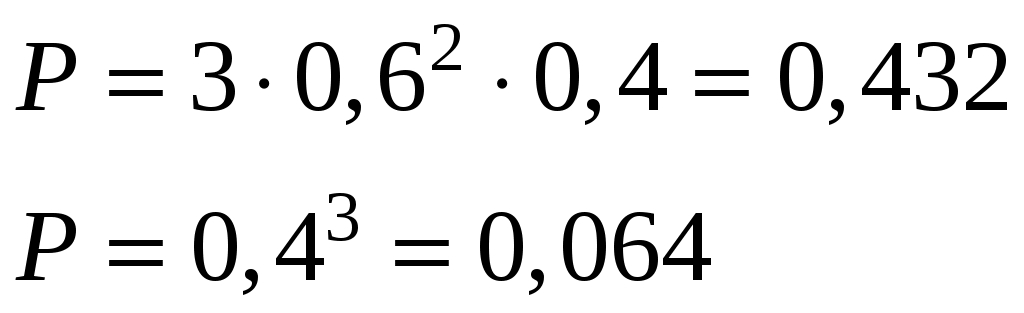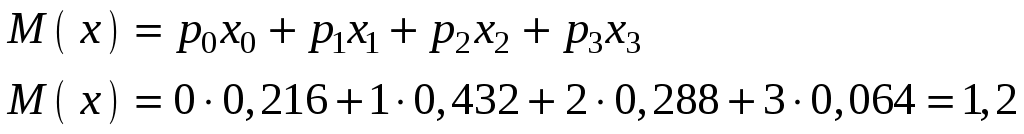





Пример 3.6. Магазин получает товар от трех независимо работающих фирм. Вероятность поставки товара от первой фирмы равна 0,4, от второй 0,3, от третьей −0,6. Составить распределение случайной величины X − числа полученных поставок, найти числовые характеристики и функцию распределения этой случайней величины.

Решение. Случайная величина X − число полученных поставок может принимать значения: 0,1,2,3. Найдем вероятности принятия каждого из этих значений.

Обозначим через (независимые события) − получение поставки товара с i-ой фирмы, где i=1,2,3, через p_i − вероятность события A.

.

Следовательно, ряд распределения имеет вид:

Х	0	1	2	3
Р	0,168	0,436	0,324	0,072

Проверим условие нормировки: .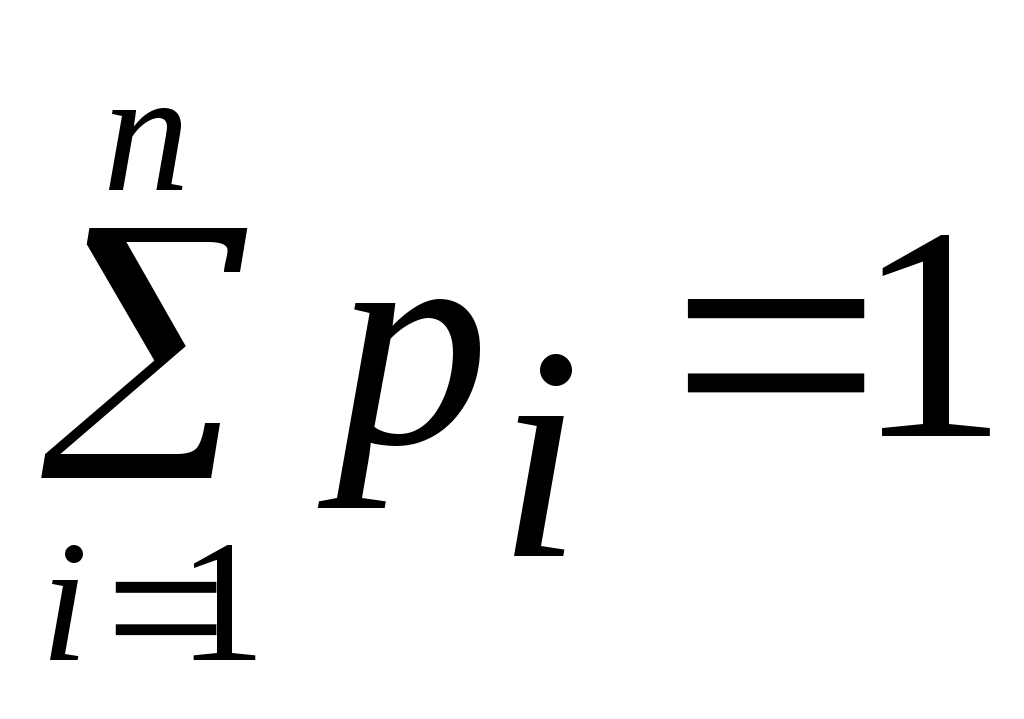

Действительно, 0,168+0,436+0,324+0,072=1

Найдем числовые характеристики: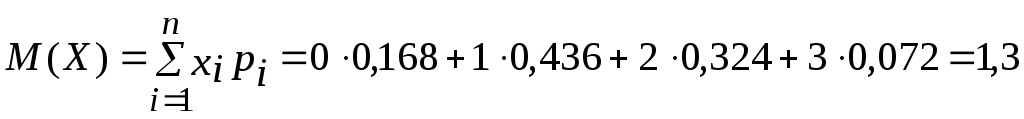



.

.

Найдем функцию распределения F(x):



Пример 3.7. Стрелок ведет стрельбу по мишени до первого попадания, имея 4 патрона. Вероятность попадания при каждом выстреле 0,6. Построить ряд распределения числа патронов, оставшихся неизрасходованными.

Решение. Случайная величина Х – число неизрасходованных патронов – имеет 4 возможных значения: 0, 1, 2, 3. Вероятности этих значений соответственно равны: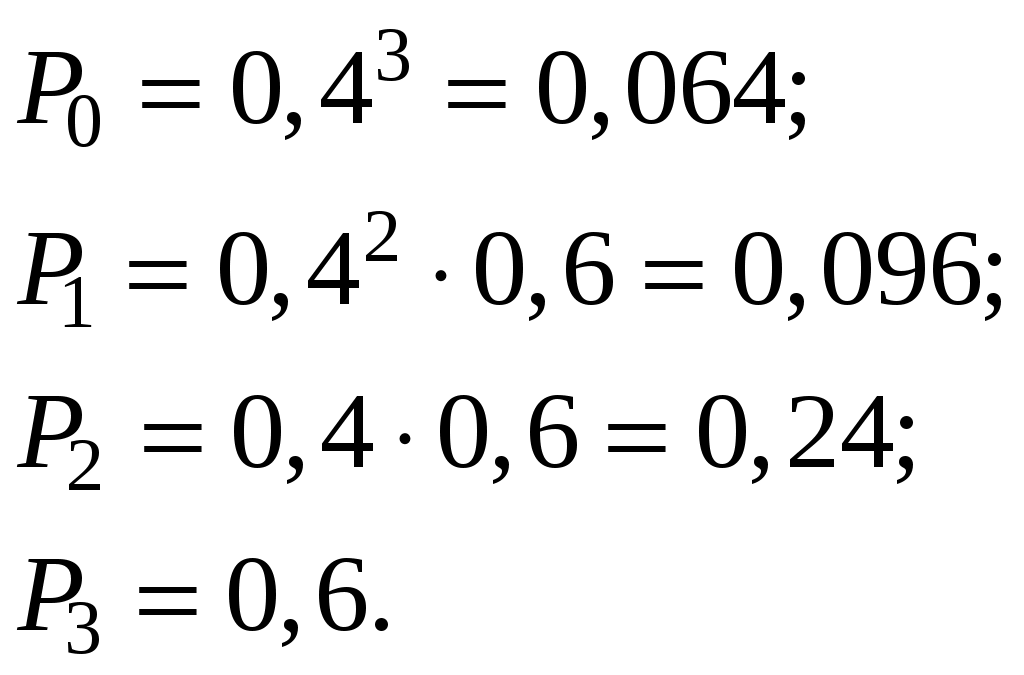

Х	0	1	2	3
Р	0,064	0,096	0,24	0,6

Пример 3.8. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте.

Решение. Дискретная случайная величина X (число отказавших элементов в одном опыте) имеет следующие возможные значения: x₁=0 (ни один из элементов устройства не отказал), x₂=1 (отказал один элемент), x₃=2 (отказали два элемента) и x₄=3 (отказали три элемента).

Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли.

Учитывая, что, по условию, n=3, p=0,1 (следовательно, q=1-0,1=0,9), получим:



;

;

.

Контроль: 0,729 + 0,243 + 0,027 + 0,001 = 1.

Напишем искомый биномиальный закон распределения X:

Х	0	1	2	3
Р	0,729	0,243	0,027	0,001

Пример 3.9. Вероятность попадания при одном выстреле равна 0,25. Найти математическое ожидание числа попаданий при 40 выстрелах.

Решение. , .

Пример 3.10. Вероятность попадания при одном выстреле Р=0,3. Определить расход снарядов, обеспечивающих математическое ожидание числа попавших снарядов, равно 6.

Решение. , .

Пример 3.11. В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Составить закон распределения числа стандартных деталей среди отобранных.

Решение. Случайная величина X – число стандартных деталей среди отобранных деталей – имеет следующие возможные значения: x₁=0; x₂=1; x₃=2. Найдем вероятности возможных значений X по формуле:

_,

гдеN – число деталей в партии, n – число стандартных деталей в партии, m – число отобранных деталей, k – число стандартных деталей среди отобранных.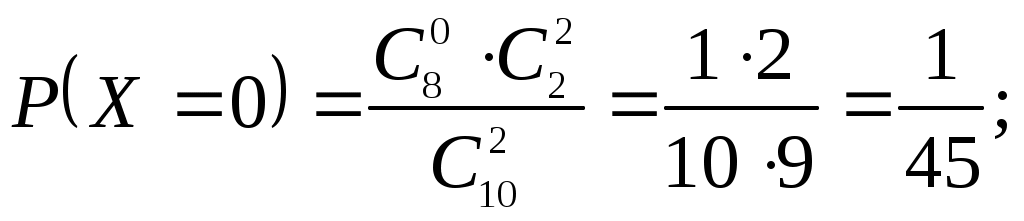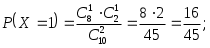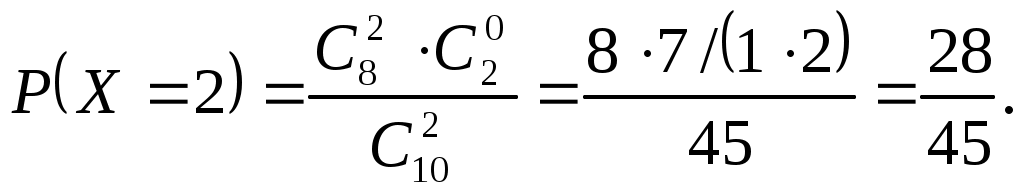







Составим искомый закон распределения:

Х	0	1	2
Р	1/45	16/45	28/45

Контроль: 1/45 + 16/45 + 28/45 = 1.

Пример 3.12. Производится 3 выстрела по мишени с вероятностями попадания в цель соответственно при каждом выстреле: Р₁=0,3; Р₂=0,4; Р₃=0,6. Найти математическое ожидание общего числа попаданий.

Решение. Число попаданий при первом выстреле есть случайная величина Х₁, принимающая два значения 0 и 1 с вероятностями 0,7 и 0,3.

численно равно вероятности попадания.

Аналогично определим: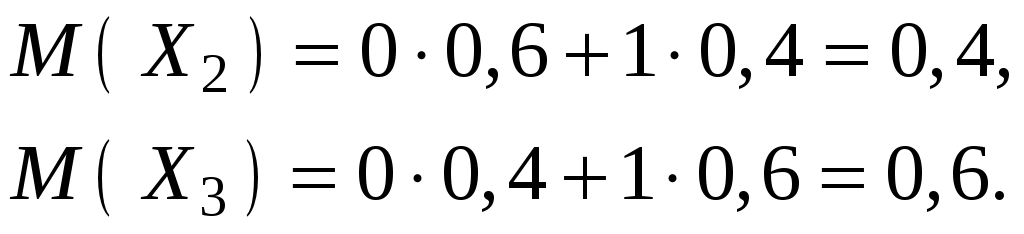



Общее число попаданий есть случайная величина Х: .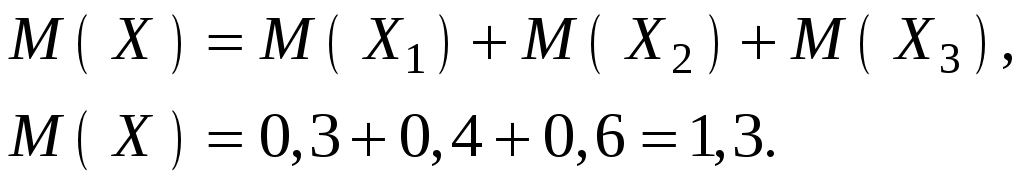



Пример 3.13. После ответа студента на вопросы экзаменационного билета экзаменатор задает студенту дополнительные вопросы. Преподаватель прекращает задавать дополнительные вопросы, как только студент обнаруживает незнание заданного вопроса. Вероятность того, что студент ответит на любой заданный дополнительный вопрос, равна 0,9. Требуется составить закон распределения случайной дискретной величины X– числа дополнительных вопросов, которые задаст преподаватель студенту;

Решение. Дискретная случайная величина X – число заданных дополнительных вопросов – имеет следующие возможные значения:

x₁=1, x₂=2, x₃=3, … , x_k=k, … .

Найдем вероятности этих возможных значений.

Величина X примет возможное значение x₁=1 (экзаменатор задаст только один вопрос), если студент не ответит на первый вопрос. Вероятность этого возможного значения равна 1–0,9=0,1. Таким образом, P(X=1)=0,1.

Величина X примет возможное значение x₂=2 (экзаменатор задаст только два вопроса), если студент ответит на первый вопрос (вероятность этого события равна 0,9) и не ответит на второй (вероятность этого события равна 0,1). Таким образом,

Аналогично найдем

Напишем искомый закон распределения:

Х	1	2	3	…	k	…
Р	0,1	0,09	0,081	…		…

Пример 3.14. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятности того, что в пути будет повреждено изделий: а) равно 3; б) менее 3; в) более 3; г) хотя бы одно.

Решение. Число n=500 велико, вероятность p=0,002 мала и рассматриваемые события (повреждение изделий) независимы, поэтому имеет месть формула Пуассона



а) Найдем λ:

Найдем вероятность того, что будет повреждено ровно 3 (k=3) изделия:



б) Найдем вероятность того, что будет повреждено менее трех изделий:



в) Найдем вероятность P того, что будет повреждено более трех деталей. События «повреждено более трех изделий» и «повреждено не более трех изделий» (обозначим вероятность этого события через Q) – противоположны, поэтому P+Q=1. Отсюда



Используя результаты, полученные выше, имеем:



г) Найдем вероятность P₁ того, что будет повреждено хотя бы одно изделие. События «повреждено хотя бы одно изделие» и «ни одно из изделий не повреждено» (обозначим вероятность этого события через Q₁) – противоположные, следовательно, P₁+Q₁=1. Отсюда искомая вероятность того, что будет повреждено хотя бы одно изделие, равна



Пример 3.15. Найти математическое ожидание дискретной случайной величины X – числа таких бросаний пяти игральных костей, в каждом из которых на двух костях появится по одному очку, если общее число бросаний равно двадцати.

Решение. Воспользуемся формулой

,

где n – общее число испытаний (бросаний пяти костей); X – число появлений интересующего нас события( на двух костях из пяти появится по одному очку) в n испытаниях; Р – вероятность появления рассматриваемого события в одном испытании.

По условию, n=20. Остаётся найти Р – вероятность того, что на гранях двух из пяти костей появится по одному очку. Эту вероятность вычислим по формуле Бернулли, учитывая, что вероятность появления одного очка на грани одной кости и, следовательно, вероятность непоявления .



Искомое математическое ожидание

.

Пример 3.16. Производится три выстрела по цели, вероятность попадания при каждом выстреле – 0,4. Определить дисперсию и среднее квадратическое отклонение случайной величины Х – числа попаданий.

Решение. Для удобства вычислений составим таблицу:

Х	0	1	2	3
Р	0,216	0,432	0,06288	0,064
Х-М(Х)	-1,2	-0,2	0,8	1,8	М(Х)=1,2
(Х-М(Х))2	1,44	0,04	0,64	3,23

.

.

Пример 3.17. Вероятность брака в некоторой партии деталей 0,0006. Какова вероятность того, что в партии из 6000 деталей число бракованных будет равно 3.

Решение. , , ,

.
Задания для самостоятельного решения
3.1. В партии 10% нестандартных деталей. Наудачу отобраны четыре детали. Написать биномиальный закон распределения дискретной случайной величины X – числа нестандартных деталей среди четырех отобранных и построить многоугольник полученного распределения.

3.2. Написать биномиальный закон распределения дискретной случайной величины X – числа появлений «герба» при двух бросаниях монеты.

3.3. Две игральные кости одновременно бросают два раза. Написать биномиальный закон распределения дискретной случайной величины X – числа выпадения четного числа очков на двух игральных костях.

3.4. В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной случайной величины X – числа стандартных деталей среди отобранных.

3.5. Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0,8. Стрелку выдаются патроны до тех пор, пока он не промахнется. Требуется составить закон распределения дискретной случайной величины X – числа патронов, выданных стрелку.

3.6. Два бомбардировщика поочередно сбрасывают бомбы на цель до первого попадания. Вероятность попадания в цель первым бомбардировщиком равна 0,7, вторым – 0,8. Вначале сбрасывает бомбы первый бомбардировщик. Составить первые четыре члена закона распределения дискретной случайной величины X – числа сброшенных бомб обоими бомбардировщиками (т.е. ограничиться возможными значениями X, равными 1, 2, 3 и 4).

3.7. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течении времени T равна 0,002. Найти вероятность того, что за время T откажут ровно 3 элемента.

Указание: Принять e^-2=0,13534.

3.8. Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 200 деталей окажется ровно четыре бракованных.

3.9. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятности того, что магазин получит разбитых бутылок: а) ровно две; б) менее двух; в) более двух; г) хотя бы одну.

Указание: Принять е^-3=0,04979.

3.10. Дискретная случайная величина X принимает три возможных значения: с вероятностью с вероятностью и с вероятностью . Найти и , зная, что

3.11. Дан перечень возможных значений дискретной случайной величины X: а также известны математические ожидания этой величины и её квадрата: ; Найти вероятности, соответствующие возможным значениям X.

3.12. В партии из 10 деталей содержится три нестандартных. Наудачу отобраны две детали. Найти математическое ожидание дискретной случайной величины X – числа нестандартных деталей среди двух отобранных.

3.13. Бросают n игральных костей. Найти математическое ожидание числа таких бросаний, в каждом из которых выпадает ровно m шестёрок, если общее число бросаний равно N.

3.14. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. В каждой партии содержится пять изделий. Найти математическое ожидание дискретной случайной величины X – числа партий, в каждой из которых окажется ровно четыре стандартных изделия, - если проверке подлежит 50 партий.

3.15. а) Устройство состоит из большого числа независимо работающих элементов с одинаковой (очень малой) вероятностью отказа каждого элемента за время T. Найти среднее число отказавших за время T элементов, если вероятность того, что за это время откажет хотя бы один элемент, равна 0,98.

б) Найти среднее число λ бракованных изделий в партии изделий, если вероятность того, что в этой партии содержится, хотя бы одно бракованное изделие, равна 0,95. Предполагается, что число бракованных изделий в рассматриваемой партии распределено по закону Пуассона.

Указание: Принять е^-3=0,05.