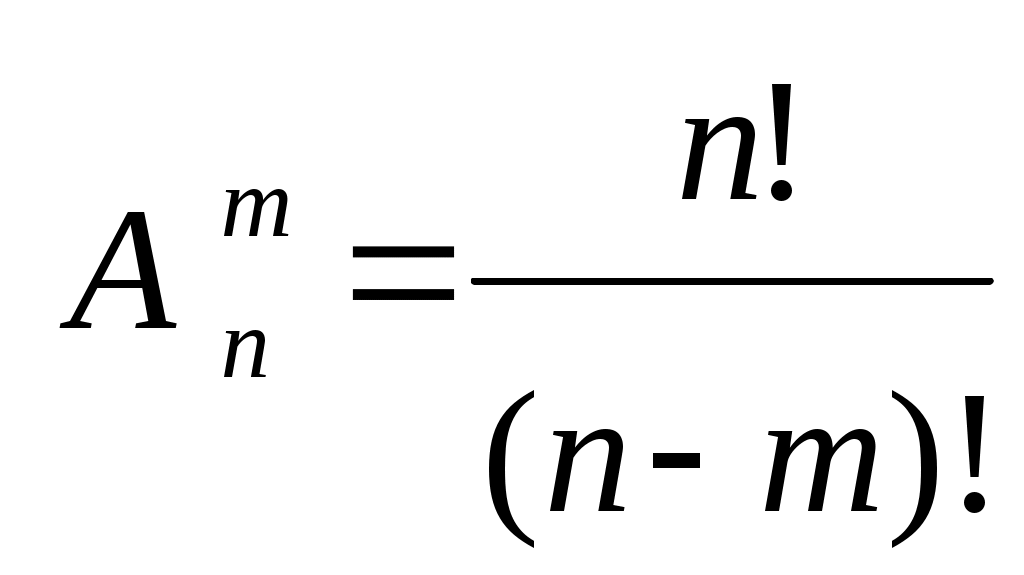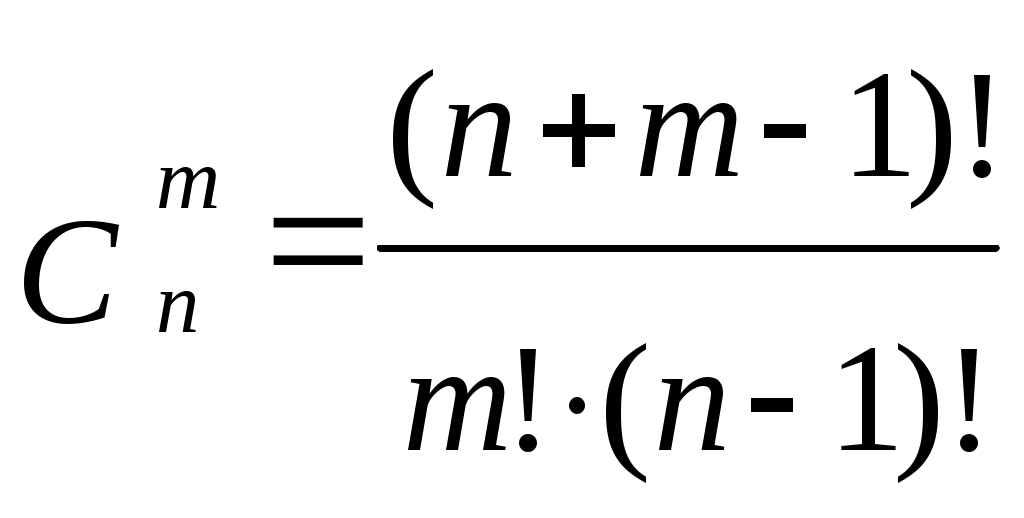матан. Теория вероятностей кажется не совсем обычной математической дисциплиной, так как имеет дело с особой категорией со случайностью. Роль случая в нашей жизни, как известно, весьма значительна

• Название: Теория вероятностей кажется не совсем обычной математической дисциплиной, так как имеет дело с особой категорией со случайностью. Роль случая в нашей жизни, как известно, весьма значительна
• Анкор: матан
• Дата: 28.03.2023
• Размер: 3.15 Mb.
• Имя файла: Matematika3_TEKST.doc
• Тип: Документы; #1021296
• страница: 1 из 8

ПРЕДИСЛОВИЕ
Теория вероятностей кажется не совсем обычной математической дисциплиной, так как имеет дело с особой категорией – со случайностью. Роль случая в нашей жизни, как известно, весьма значительна. Отдаст ли клиент коммерческого банка кредит в установленные сроки, попадет ли купленный вами автомобиль в аварию в течение ближайшего года, испытает ли ваше здоровье какое-либо потрясение в ближайшие несколько лет, – во всех подобных случаях сделать уверенный прогноз затруднительно. Это заставляет нас в каждом отдельном случае оценивать риск и прибегать к различным страховочным процедурам. Соответствующие расчеты основаны на теории вероятностей, являющейся в настоящее время краеугольным камнем всех естественных наук.

Как математическая наука теория вероятностей возникла в середине XVII века с работами таких ученых, как Ферма, Паскаль. В России первые исследования по теории вероятностей были выполнены к середине XIX века. Они связаны с именами замечательных русских ученых: Лобачевского, Остроградского и Буняковского. Именно Буняковский дал терминологию новой науки на русском языке, и до сих пор она не подвергалась существенным изменениям. После работы выдающегося русского математика и механика Чебышева и его учеников Ляпунова и Маркова теорию вероятностей во всем мире стали называть «русской наукой». Эти замечательные традиции были продолжены советскими учеными.

Сейчас, пожалуй, нет области знания, в которой не использовались бы методы теории вероятностей. Выводы теории вероятностей применяются в физике и в химии, астрономии и геодезии, медицине и биологии, военной науке и космонавтике, теории стихосложения и лингвистике, психологии и теории обучения и т.д. На основе вероятностных методов появился целый ряд новых наук: теория информации, теория надежности, статистический контроль качества, планирование эксперимента и др. Теория вероятностей является математической основой кибернетики, развитие которой, в свою очередь, способствовало еще большему возрастанию прикладного значения теории вероятностей.

Предметом изучения теории вероятностей являются случайные явления и физические закономерности массовых случайных явлений. Применение теории вероятностей в экономике, бухгалтерском учете, менеджменте имеет особенно важное значение при изучении и исследовании теоретических и практических вопросов. Отбор иллюстративного материала в учебном пособии отражает его предназначенность в первую очередь для экономистов, бухгалтеров и менеджеров. Это подтверждают как отдельные примеры глав 1 – 4, так и целые главы. Систематическое использование торгово-экономических приложений пронизывает весь материал учебного пособия.


Часть I. СЛУЧАЙНЫЕ СОБЫТИЯ
Глава 1. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

1. 
   Основные понятия
   

Теория вероятностей – это математическая наука, изучающая закономерности случайных явлений, наблюдаемых при массовых повторениях испытаний.

Случайное явление – это такое явление, которое при неоднократном воспроизведении опыта протекает каждый раз по-разному.

Например: изменение курса валют, подбрасывание монеты или игрального кубика, стрельба по мишени.

Одним из основных понятий теории вероятностей является событие.

Событием называется результат опыта (испытания), который в результате опыта может произойти или не произойти.

Например: Повышение курса валют, попадание в мишень при выстреле, выпадение двух очков на грани игрального кубика и т.д.

События принято обозначать большими буквами латинского алфавита: А, В, С…
Классификация событий

1. 
   Событие называется достоверным, если при повторениях опыта оно всегда происходит.
   
2. 
   Событие называется невозможным, если при повторениях опыта оно никогда не происходит.
   
3. 
   Событие называется случайным (или возможным), если при повторениях опыта оно может произойти, а может не произойти.
   
4. 
   События называются равновозможными, если условия их появления одинаковы и нет оснований считать какое-либо из них более возможным, чем другие.
   
5. 
   Два события называются несовместными (совместными), если появление одного их них исключает (не исключает) появление другого.
   
6. 
   Два несовместных события, из которых одно обязательно произойдет, называются противоположными. Противоположное событие для события А обозначается .
   
7. 
   Отдельное, единичное событие, которое является конечным результатом какого-либо явления, называется простым (элементарным) событием.
   
8. 
   Событие называется сложным, ели оно состоит из совпадения или последовательного появления двух или нескольких простых событий.
   
9. 
   Несколько событий образуют полную группу событий, если в результате опыта обязательно наступает хотя бы одно из них. На практике широкое применение находит полная группа несовместных событий.
   

2. 
   Алгебра событий
   

Суммой (или объединением) событий А и В называется событие С, состоящее в появлении события А, или события В, или обоих вместе.

Суммой (или объединением) нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.

Обозначение суммы: , .

Произведением (или пересечением) событий А и В называется событие С, состоящее в появлении события А и события В.

Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Обозначение произведения: , .

Например. Фирма получает заказ на поставку товара от двух магазинов.

Событие – первый магазин сделал заказ, событие – второй магазин сделал заказ. Рассмотрим следующие события.

Событие – два магазина сделали заказ на поставку товара, т.е. .

Событие – один магазин сделал заказ на поставку товара, т.е. .

3. 
   Частота события
   

Пусть произведена серия из n опытов, в каждом из которых могло появиться или не появиться событие А. Допустим, что событие А появилось m раз.

Частотой события А называется отношение числа появлений события к числу всех произведенных опытов.

Частота обозначается и по определению .

Например. В серии из 15 выстрелов получено 7 попаданий. Определить частоту попаданий.

Событие А – попадание, , тогда частота попаданий .

Свойства частоты

1. 
   .
   
2. 
   Частота достоверного события равна единице.
   
3. 
   Частота невозможного события равна нулю.
   
4. 
   Частота события изменяется с изменением числа опытов.
   

4. 
   Вероятность события
   

Вероятность является одним из основных понятий теории вероятностей. Вероятность события дает численную меру объективной возможности появления события. Формулу для непосредственного вычисления вероятности события, дает классическое определение вероятности.

Вероятностью события А называется отношение числа благоприятствующих этому событию случаев к общему числу всех единственно возможных и равновозможных случаев:

.

В этой формуле Р(А) – вероятность события А, n – общее число случаев (исходов испытания), m – число случаев, благоприятствующих событию А.

Случай называется благоприятствующим событию А, если появление этого случая влечет за собой появление события А.

Например. В ящике находится 150 стандартных и 50 нестандартных деталей. Какова вероятность того, что взятая наугад деталь окажется нестандартной?

Событие А – нестандартная деталь.

Всего деталей – это общее число случаев. Число благоприятствующих событию А случаев . Тогда, .

Свойства вероятности события

1. 
   .
   
2. 
   Вероятность достоверного события равна единице.
   
3. 
   Вероятность невозможного события равна нулю.
   
4. 
   Вероятность события не зависит от числа проведенных опытов и остается постоянной до тех пор, пока условия опыта не изменятся.
   

Связь частоты и вероятности

При увеличении числа опытов частота события все более теряет случайный характер. Случайные обстоятельства, свойственные отдельному опыту, в большой массе опытов взаимно погашаются, и частота проявляет тенденцию стабилизироваться, колеблясь около некоторого числа. Длительные наблюдения показали, что это постоянное число есть вероятность появления события. Вероятность события есть, по сути дела, предел частоты при увеличении числа опытов, а потому частоту называют статистической вероятностью.
Геометрическая вероятность
На практике часто встречаются испытания, исходы которых являются или неравновозможными, или их число бесконечно. Так, если испытание состоит в том, что сигнальщик в течение часа должен принять мгновенный световой сигнал, то его возможными исходами можно считать появление сигнала в любой момент времени в течение этого часа. Множество исходов испытания такого типа бесконечно, оно может быть иллюстрировано геометрически в виде совокупности точек отрезка прямой, плоской фигуры или пространственного тела. Такую схему испытаний принято называть геометрической.

Пусть в результате испытания наудачу выбирается точка в области S. Требуется найти вероятность того, что точка окажется в области s, являющейся частью области S.

Пусть исходы испытаний распределены равномерно, т.е. можно считать, что вероятность попадания наудачу выбранной точки из области S в какую-либо часть s этой области пропорциональна мере этой части и не зависит от ее расположения и формы. Тогда,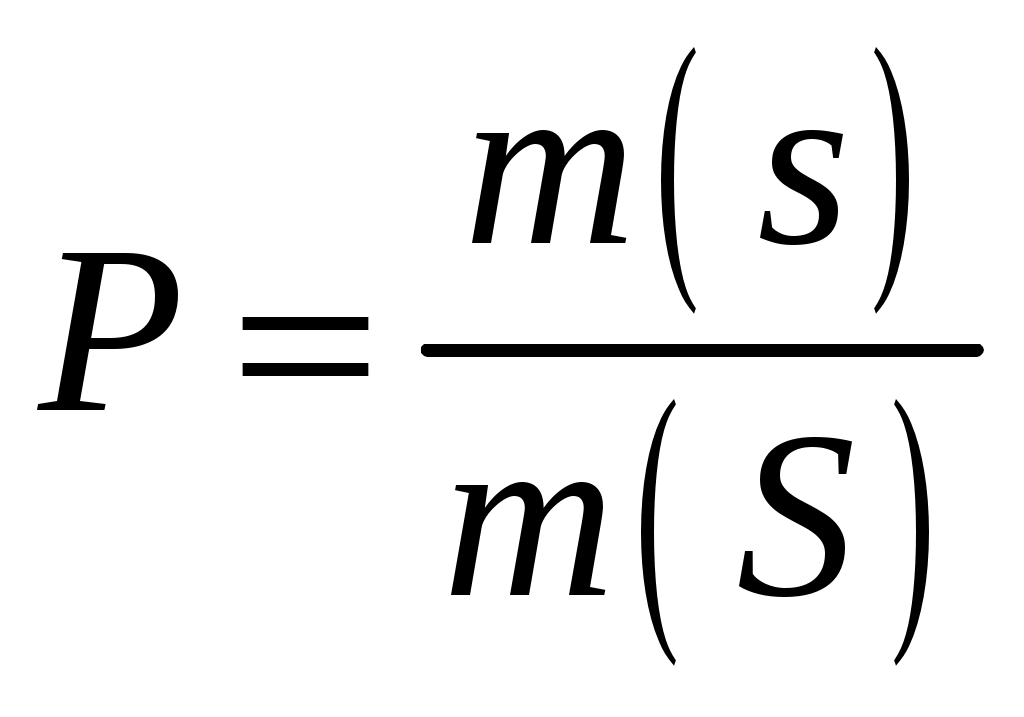

,

где и есть меры соответствующих областей, выраженные в единицах длины, площади или объема.

5. 
   Элементы комбинаторики
   

При подсчете общего числа случаев – n и число случаев, благоприятствующих событию А – m, часто приходится рассматривать различные комбинации из элементов некоторого множества.

Различные группы, составленные из элементов какого-либо множества и отличающиеся одна от другой порядком элементов или самими элементами, называется соединениями.

Соединения называются упорядоченными, если порядок элементов играет роль, и неупорядоченными, если порядок элементов роли не играет.

Соединения могут быть без повторений, если элементы повторяться не могут, и с повторениями, если элементы в соединении повторяются.

Например. Телефонный номер 263-03-96 – упорядоченное соединение с повторениями из 10 цифр по 7.

Соединения бывают трех видов: размещения, перестановки и сочетания.

Упорядоченные соединения из n элементов по m называются размещениями.

Число размещений обозначается 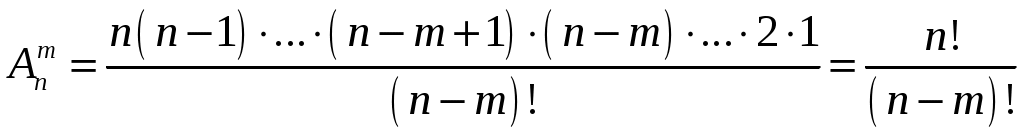и вычисляется по формуле:

.

Например. Сколько можно составить трехзначных чисел из нечетных цифр, если каждую из этих цифр использовать только один раз?

, , ,

.

Соединения, состоящие из одних и тех же элементов и отличающиеся только порядком элементов, называются перестановками.

Перестановки – это размещения, у которых

Число перестановок обозначается и вычисляется по формуле:

.

Например. Сколько пятизначных чисел можно записать при помощи цифр 1, 2, 3, 4, 5, если каждая цифра входит в изображение числа только один раз?

.

Неупорядоченные соединения из n элементов по m называются сочетаниями.

Число перестановок обозначается .

Составим все сочетания из n элементов по m. В каждом из полученных соединений возможными способами, произведем перестановку элементов. Получим размещ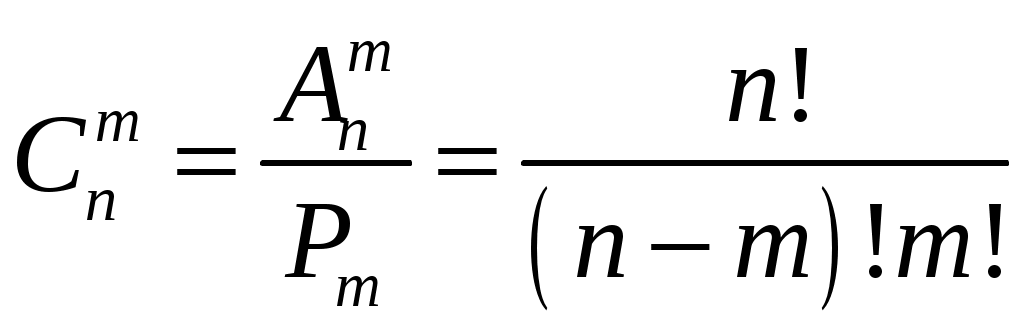ений, поэтому:

,

отсюда:

.

Например. В группе 25 студентов. Сколькими способами можно назначить из них дежурных в составе трех человек?

.
Применение формул комбинаторики для вычисления вероятностей
При решении задач по данной теме рекомендуется использовать классическую формулу для вычисления вероятности события .

Число случаев m и n удобно находить, пользуясь таблицей.

Соединения	Упорядоченные	Неупорядоченные
Без повторений
С повторениями

Например. В партии из n изделий m бракованных. Определить вероятность того, что среди выбранных l изделий ровно k окажутся бракованными ( , , ).

Решение: Обозначим через А появление k бракованных изделий среди выбранных наудачу l изделий.

Вероятность события А находим по формуле .

Общее число случаев n= , т.к. любая комбинация из n изделий по l имеет одинаковую возможность появления.

Число случаев, благоприятствующих событию А: m= , т.к. всех б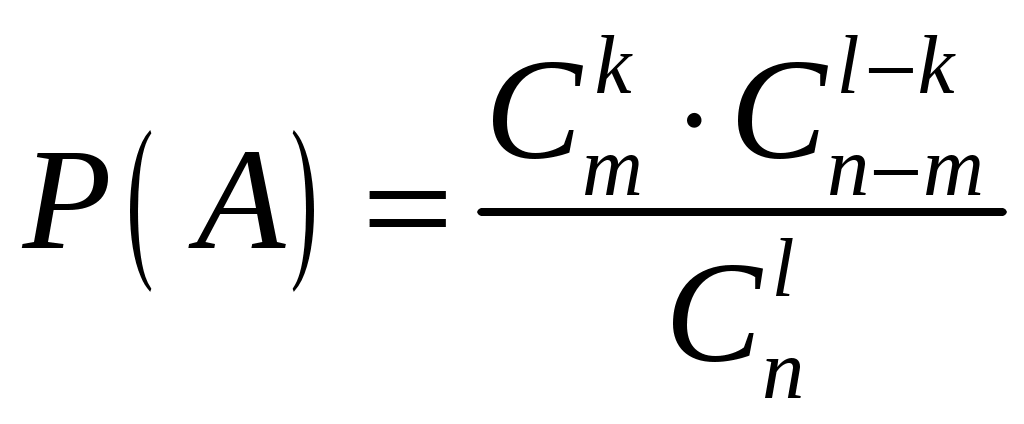ракованных изделий m, то число способов, которыми можно выбрать k бракованных изделий равно , но каждый из этих способов будет дополняться любой группой изделий из числа способов, которыми можно вынуть оставшиеся годных из общего числа годных изделий. Число таких групп равно .

Поэтому:

.
1.6. Примеры решения задач к главе 1
Пример 1.1. В коробке находится 120 ручек с синим стержнем и 60 с красным. Какова вероятность того, что взятая наугад ручка окажется с красным стержнем?

Решение: Событие А – ручка с красным стержнем.

Для нахождения вероятности события А применяем формулу:

, где , .

Тогда .

Пример 1.2. В ящике 21 стандартная и 10 нестандартных деталей. При перевозке одна деталь утеряна. Наудачу извлеченная (после перевозки) из ящика деталь оказалась стандартной. Найти вероятность того, что была утеряна: а) стандартная деталь; б) нестандартная деталь.

Решение. а) Событие А – утеряна стандартная деталь.

Так как извлеченная стандартная деталь не могла быть утеряна, то могла быть потеряна любая из остальных 30 деталей: .

Причем среди них было 20 стандартных: .

Вероятность того, что была потеряна стандартная деталь: .

б) Событие В – утеряна нестандартная деталь.

Среди 30 деталей, каждая из которых могла быть утеряна, было 10 нестандартных. Вероятность того, что потеряна нестандартная деталь: .

Пример 1.3. Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 3 (событие А).

Решение. Событие А – сумма выпавших очков равна 3.

Общее число равновозможных исходов равно (каждое число очков, выпавших на одной кости, может сочетаться со всеми числами очков, выпавших на другой кости).

Среди этих исходов благоприятствуют событию А только два исхода (в скобках указаны числа выпавших очков: 1; 2 и 2;1), т.е. .

Тогда искомая вероятность .

Пример 1.4. В отделе из 7 человек нужно выбрать начальника и его заместителя. Найти вероятность того, что ими окажутся два вполне определенных человека.

Решение. Событие А – начальником и его заместителем окажутся 2 вполне определенных человека.

Воспользуемся классической формулой для вычисления вероятности события .

Т.к. соединения в данном случае упорядоченные и без повторений, то , а m=1.

То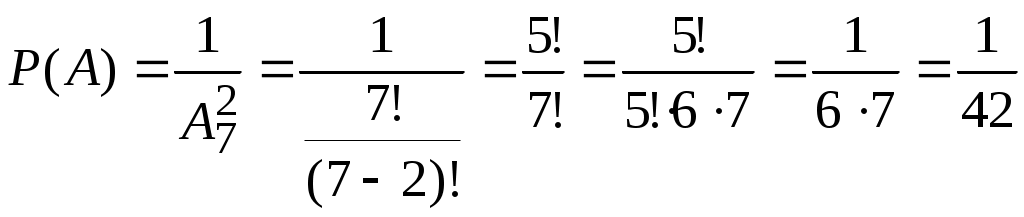гда .

Пример 1.5. Найти вероятность того, что при бросании трех игральных костей шестерка выпадет на одной (безразлично какой) кости, если на гранях двух других костей выпадут числа очков, не совпадающие между собой (и не равные шести).

Решение. Т.к. соединения в данном случае неупорядоченные и без повторений, то общее число элементарных исходов испытания равно числу сочетаний из шести элементов по три, т. е. .

Число исходов, благоприятствующих появлению шестерки на одной грани и различного числа очков (не равного шести) на гранях двух других костей, равно числу сочетаний из пяти элементов по два, т. е. .

Искомая вероятность равна отношению числа исходов, благоприятствующих интересующему нас событию, к общему числу возможных элементарных исходов: .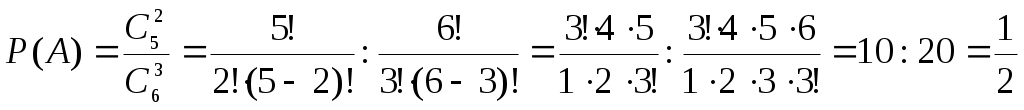

Пример 1.6. Из 5 экономистов и 6 бухгалтеров необходимо выбрать группу из 7 человек. Какова вероятность того, что в эту группу попадут 4 экономиста и 3 бухгалтера?

Решение. Событие А – в комитете окажутся 4 экономиста и 3 бухгалтера.

Воспользуемся классической формулой для вычисления вероятности события , где m – число благоприятных событию А случаев, n – число всех случаев.

Т.к. выборка в данном случае неупорядоченная и без повторений, то 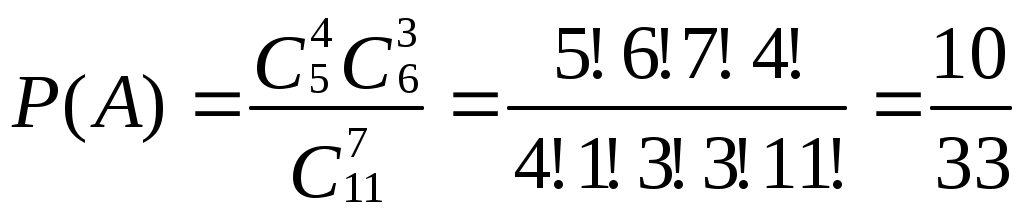, , следовательно, .

Пример 1.7. В ящике 20 сигнальных ракет, из которых 6 красного цвета остальные зеленого цвета. Какова вероятность того, что среди взятых наудачу пяти ракет 3 окажутся красного цвета?

Решение: Событие А – среди взятых наудачу пяти ракет 3 окажутся красного цвета.

, где , .

То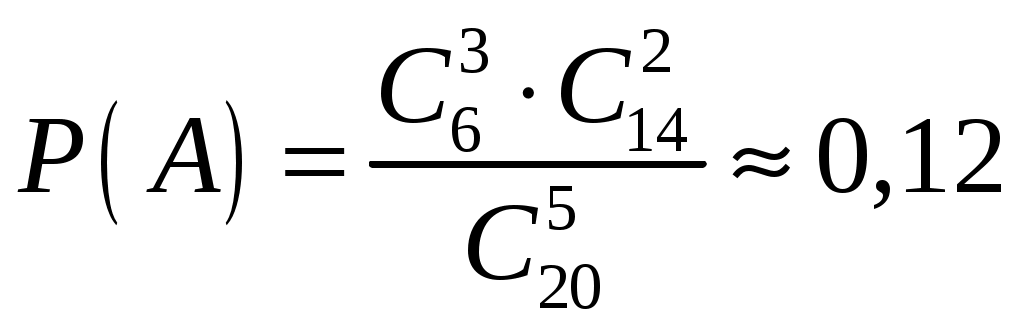гда .

Пример 1.8. В ящике 10 одинаковых деталей, помеченных номерами 1. 2,…,10. Наудачу извлечены шесть деталей. Найти вероятность того, что среди извлеченных деталей окажутся: а) деталь № 1; б) детали № 1 и № 2.

Решение: а) Событие А – среди извлеченных деталей окажется деталь №1.

Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь шесть деталей из десяти, т. е. .

Найдем число исходов, благоприятствующих интересующему нас событию: среди отобранных шести деталей есть деталь №1 и, следовательно, остальные пять деталей имеют другие номера. Число таких исходов равно числу способов, которыми можно отобрать пять деталей из оставшихся девяти, т.е. .

Искомая вероятность равна отношению числа исходов, благоприятствующих рассматриваемому событию, к общему числу возможных элементарных исходов: .

б) Событие В – среди извлеченных деталей окажется детали №1 и №2.

Число исходов, благоприятствующих событию В (среди отобранных деталей есть детали №1 и №2, следовательно, четыре детали имеют другие номера), равно числу способов, которыми можно извлечь четыре детали из оставшихся восьми, т. е. .

Искомая вероятность .

Пример 1.9. При проверке в библиотеке обнаружено 5 бракованных книг в партии из случайно отобранных 100 книг. Найти частоту появления бракованных книг.

Решение. Событие А – книга бракованная.

Частота события А равна отношению числа испытаний, в которых появилось событие А к общему числу произведенных испытаний:

.

Пример 1.10. При выполнении спортивного упражнения стрелок в первой серии из 30 выстрелов поразил 28 мишеней, а во второй серии из 30 выстрелов – 24 мишени. Какова частота поражения мишеней в каждой серии и при выполнении всего упражнения?

Решение: а) ; б) ; с) .

Пример 1.11. Определить число промахов, если известно, что произведено 16 выстрелов, а частота попадания равна , , 1.

Решение: => ; n=16, .

1. 
   ; , .
   
2. 
   ; , .
   
3. 
   ; , .
   

Пример 1.12. Из скольких элементов можно составить 72 размещения по 2 элемента в каждом?

Решение: .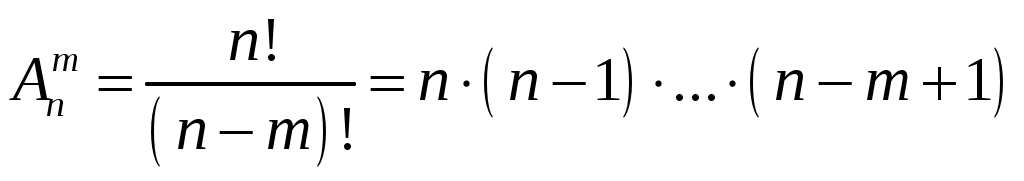

, , => .

Пример 1.13. Сколько различных чисел можно записать при помощи цифр 0, 1, 3, 4, 7?

Решение: Количество таких чисел определяется разностью: , где – число перестановок из пяти указанных цифр, а – количество чисел из указанных цифр, если цифра «0» оказывается на первом месте.

Пример 1.14. Самолет бомбит объект, занимающий площадь м². Зона бомбометания – эллипс с полуосями 200 м и 250 м. Определить вероятность прямого попадания в объект одной бомбой, если предполагать, что попадание бомбы в любую точку зоны бомбометания равновозможно.

Решение. Событие А – попадание бомбой в объект. Вероятность события находим по формуле геометрической вероятности: 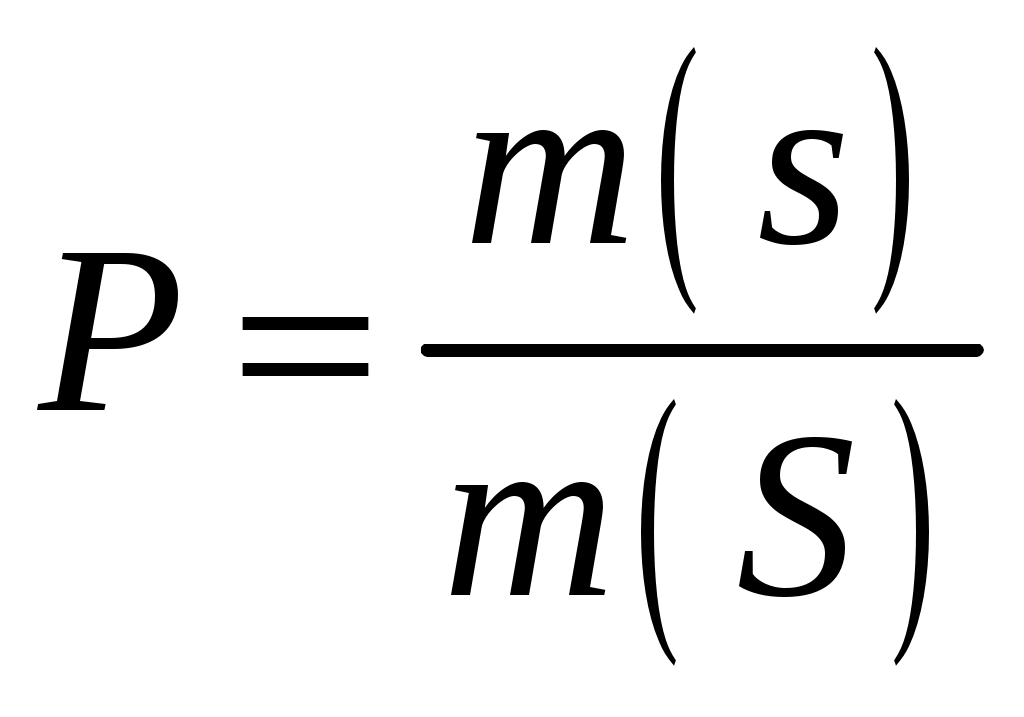, где и есть меры соответствующих областей, выраженные в данном случае в единицах площади.

Тогда .
Задания для самостоятельного решения
1.1. Задумано двузначное число. Найти вероятность того, что задуманным числом окажется: а) случайно названное двузначное число; б) случайно названное двузначное число, цифры которого различны.

1.2. Брошены две игральные кости. Найти вероятности следующих событий: а) сумма выпавших очков равна семи; б) сумма выпавших очков равна восьми, а разность – четырем; в) сумма выпавших очков равна восьми, если известно, что их разность равна четырем; г) сумма выпавших очков равна пяти, а произведение – четырем.

1.3. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик имеет окрашенных граней: а) одну; б) две;

в) три.

1.4. В коробке шесть одинаковых, занумерованных кубиков. Наудачу по одному извлекают все кубики. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.

1.5. В пачке 20 перфокарт, помеченных номерами 101, 102, . . . , 120 и произвольно расположенных. Перфораторщица наудачу извлекает две карты. Найти вероятность того, что извлечены перфокарты с номерами 101 и 120.

1.6. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.

1.7. В конверте среди 100 фотокарточек находится одна разыскиваемая. Из конверта наудачу извлечены 10 карточек. Найти вероятность того, что среди них окажется нужная.

1.8. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены четыре детали. Найти вероятность того, что среди извлеченных деталей: а) нет бракованных; б) нет годных.

1.9. Устройство состоит из пяти элементов, из которых два изношены. При включении устройства включаются случайным образом два элемента. Найти вероятность того, что включенными окажутся неизношенные элементы.

1.10. Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.

1.11. В цехе работают шесть мужчин и четыре женщины. По табельным номерам наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины.

1.12. На складе имеется 15 кинескопов, причем 10 из них изготовлены Львовским заводом. Найти вероятность того, что среди пяти взятых наудачу кинескопов окажутся три кинескопа Львовского завода.

1.13. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов пять отличников.

1.14. В коробке пять одинаковых изделий, причем три из них окрашены. Наудачу извлечены два изделия. Найти вероятность того, что среди двух извлеченных изделий окажутся: а) одно окрашенное изделие; б) два окрашенных изделия.

1.15. В «секретном» замке на общей оси четыре диска, каждый из которых разделен на пять секторов, на которых написаны различные цифры. Замок открывается только в том случае, если диски установлены так, что цифры на них составляют определенное четырехзначное число. Найти вероятность того, что при произвольной установке дисков замок будет открыт.

1.16. По цели произведено 20 выстрелов, причем зарегистрировано 18 попаданий. Найти частоту попаданий в цель.

1.17. При испытании партии приборов частота годных приборов оказалась равной 0,9. Найти число годных приборов, если всего было проверено 200 приборов.

1.18. На курсах повышения квалификации бухгалтеров учат определять правильность накладной. В качестве проверки преподаватель предлагает обучающимся проверить 10 накладных, 4 из которых содержат ошибки. Он берет наугад из этих 10 две накладные и просит проверить. Какова вероятность того, что они окажутся а) обе ошибочные, б) одна ошибочная, а другая нет?

1.19. В магазине работают 2 мужчин и 7 женщин. Трое из них должны пойти в отпуск летом. Кто именно – определяется жребием. Найти вероятность того, что летом в отпуск пойдет хотя бы один мужчина.

1.20. Баночки маргарина и майонеза имеют одинаковый вес и внешний вид. Для приготовления салата требуется 3 банки майонеза и 1 банка маргарина. Из ящика, в котором 8 банок маргарина и 5 банок майонеза, наудачу извлекли 4 банки. Какова вероятность того, что из них можно приготовить данное блюдо?

1.21. В пачке 10 тетрадей, среди них 4 тетради в клетку, а остальные в линейку. Найти вероятность того, что среди наудачу взятых трех тетрадей хотя бы одна будет в клетку.

1.22. Имеются 4 столбика и 6 ведер с красками разных цветов. Каждый столбик окрашивается краской из наудачу взятого ведра (при этом может получиться так, что разные столбики будут окрашены одной и той же краской). Найти вероятность того, что все столбики будут окрашены разными красками.

1.23. В коробке 10 плиток шоколада, среди которых 7 с орехами. Наудачу взяли 3 плитки. Найти вероятность того, что среди них хотя бы одна плитка с орехами.

1.24. Для приготовления блюда нужно взять по одному пакету смеси полуфабриката №1, №2, №3. Какова вероятность, что технология не будет нарушена, если имеется 4 пакета смеси №1, 2 пакета смеси №2 и 3 пакета смеси №3 и если 3 пакета выбираются из них наудачу?

1.25. В библиотеке имеется 5 методичек выпуска 1992 года и 9 методичек по той же теме выпуска 1996 года. Библиотекарь выдает на угад 6 методичек. Какова вероятность того, что первой пришедшей группе будет выдано 5 методичек выпуска 1996 года, если библиотекарь берет методички произвольно?

1.26. Шесть различных счетов, среди которых 2 оформленных с ошибками, поступили на проверку. Какова вероятность, что эти два счета будут лежать в данной пачке счетов рядом?

1.27. На склад поступило 15 кофемолок и 10 кофеварок. Для контроля наудачу взяли 3 вещи. Найти вероятность того, что среди взятых: а) только одна кофемолка, б) хотя бы одна кофемолка.

1.28. На экзамене три студента получили за ответ «отлично», десять студентов «хорошо» и восемь – «удовлетворительно». Для аттестации из этой группы наудачу отобрали 7 человек. Какова вероятность того, что среди них будут два «отличника», 3 «хорошиста» и 2 «троечника»?

1.29. Среди 10 документов, поступивших в офис, два оформлены с ошибками. Для проверки наудачу взяли 4 документа. Какова вероятность того, что среди них окажется а) хотя бы один неверно оформленный документ, б) только один неверно оформленный документ?

1.30. К двум ревизорам на проверку поступило 16 счетов, среди которых два счета содержат неточности. Какова вероятность того, что эти два счета а) попали к одному ревизору, б) попали к разным ревизорам, если все документы ревизоры разделили поровну?

1.31. В лотерее 15 билетов, из которых 6 выигрышных. Какова вероятность выиграть хотя бы 2 раза, купив 3 билета?

1.32. В бухгалтерии работают 3 мужчин и 5 женщин. На курсы повышения квалификации в соседний город нужно послать 4 человека. Наудачу по списку их называют в отделе кадров. Какова вероятность того, что среди отобранных а) будут только женщины, б) будет хотя бы один мужчина?

1.33. В группу принесли 20 методичек по математике, среди которых 3 оказались по линейной алгебре. Студент наудачу взял две методички. Какова вероятность того, что среди взятых а) нет методичек по линейной алгебре, б) есть одна по линейной алгебре?

1.34. В пачке 8 тетрадей, среди которых 5 тетрадей в клетку, остальные в линейку. Студент наудачу берет 3 тетради. Какова вероятность того, что среди взятых а) одна в линейку, б) все тетради в клетку?

1.35. Из 5 футболистов, 6 конькобежцев и 3 шахматистов нужно сформировать случайным образом комитет из 4 членов. Какова вероятность того, что в комитете окажутся 2 футболиста, конькобежец и шахматист?

1.36. Из 9 человек, выбранных в профком, нужно избрать председателя профкома, председателя ревизионной комиссии и секретаря. Какова вероятность того, что ими окажутся три вполне определенных человека?