матан. Теория вероятностей кажется не совсем обычной математической дисциплиной, так как имеет дело с особой категорией со случайностью. Роль случая в нашей жизни, как известно, весьма значительна
 Скачать 3.15 Mb.
|
|
Глава 2. ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ Теоремы сложения и умножения вероятностей Теорема 1. (Теорема сложения вероятностей несовместных событий). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:  .Следствие 1.1. Если событие А1, А2,…, Аn образуют полную группу несовместных событий, то сумма их вероятностей равна единице: 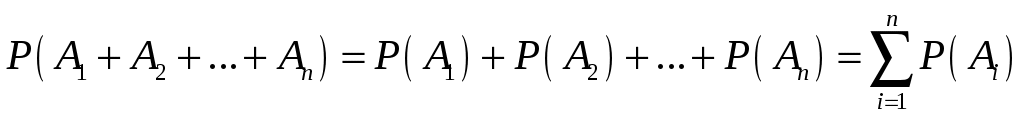 , 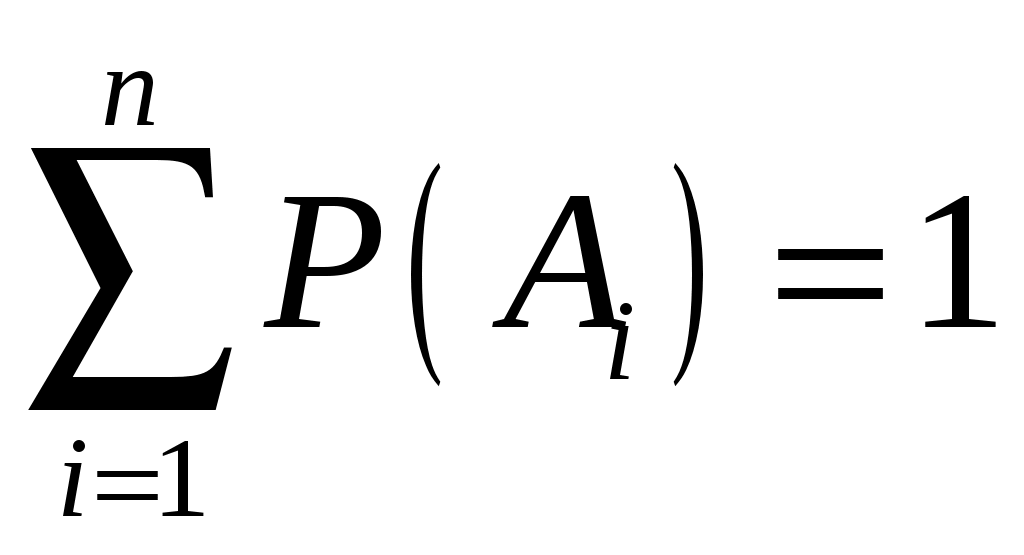.Следствие 1.2. Сумма вероятностей противоположных событий равна единице:  .Следствие 2 есть частный случай первого следствия. Оно имеет большое применение в решении задач теории вероятностей. Иногда оказывается легче вычислить вероятность противоположного события, чем вероятность прямого события. Поэтому очень часто используют формулу, выражающую вероятность события А через вероятность противоположного события  (или наоборот): .Замечание 1. При решении задач вероятность события обозначают p, а вероятность противоположного события q. Тогда предыдущие формулы принимают вид:  .Теорема 2. (Теорема сложения вероятностей совместных событий). Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:  .Замечание 2. Теоремы 1, 2 могут быть обобщены на любое конечное число несовместных (совместных) событий. Например, для трех совместных событий: Р(А+В+С)= Р(А)+Р(В)+Р(С)–Р(АВ)–Р(АС)–Р(ВС)+Р(АВС). Введем несколько понятий, которые необходимы для формулировки теоремы умножения вероятностей. Событие А называется независимым от события В, если вероятность появления события А не зависит от того, произошло событие В или нет. Например. Два студента сдают экзамен. Пусть событие А – первый студент сдал экзамен, В – второй студент сдал экзамен. Вероятность события А не зависит от того, произошло или нет событие В, т.е. А не зависит от В (и наоборот). Два события называются зависимыми, если вероятность появления одного из них зависит от наступления или ненаступления другого события. Например. В библиотеке 80 учебников, из них 70 – новые. Наудачу берут один учебник, затем, не возвращая его, испытание повторяют. Рассмотрим события: А – появление нового учебника при первом испытании, В – появление нового учебника при втором испытании. Если А произошло, то в библиотеке останется 79 учебников, причем новых будет 69 и тогда  .Если же при первом испытании А не произошло, то на 79 оставшихся учебников будет 70 новых и тогда  .Данный пример демонстрирует вычисление вероятности зависимых событий. Вероятность события В, вычисленная при условии, что имело место событие А, называется условной вероятностью события В. Обозначение:  .Если события А и В независимы, то  и  .Теорема 3. (Теорема умножения вероятностей зависимых событий). Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло:  .Следствие 3.1. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляют в предложении, что все предыдущие события уже наступили. Например, для трех событий:  .Теорема 4. (Теорема умножения вероятностей независимых событий). Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:  .Следствие 4.1. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий. Например, для трех событий:  .Вероятность появления хотя бы одного события Несколько событий называются независимыми в совокупности, если каждое из них и любая комбинация остальных событий, либо часть из них, есть события независимые. Теорема. Вероятность появления хотя бы одного из событий А1, А2,…, Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий  . или  .Следствие. Если события А1, А2,…, Аn имеют одинаковую вероятность появления p, то события имеют вероятность  , тогда .Формулы полной вероятности Пусть событие А может произойти совместно с одним из событий Н1, Н2,…, Нn, образующих полную группу несовместных событий. События Н1, Н2,…, Нn принято называть гипотезами. Теорема. Вероятность события А, которое может произойти с одной из гипотез Н1, Н2,…, Нn, равна сумме произведений вероятностей каждой из этих гипотез на соответствующие им условные вероятности события А: 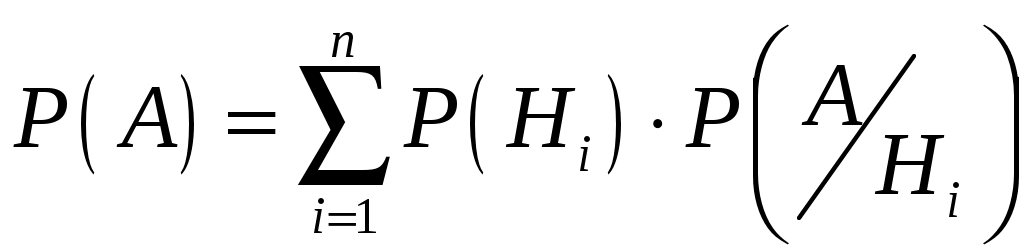 .Эта формула называется формулой полной вероятности. Формула полной вероятности является одним из эффективных методов подсчета вероятностей, с помощью этой формулы решается широкий круг задач. Формула Байеса (теорема гипотез) Пусть имеется полная группа несовместных событий – гипотез Н1, Н2,…, Нn. Вероятности этих гипотез до опыта известны и равны соответственно:  .Произведен опыт, в результате которого появилось событие А. Необходимо найти вероятность гипотезы  после проведения опыта (т.е. при условии, что событие А произошло). Иными словами, необходимо найти условную вероятность  для гипотезы .Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события: 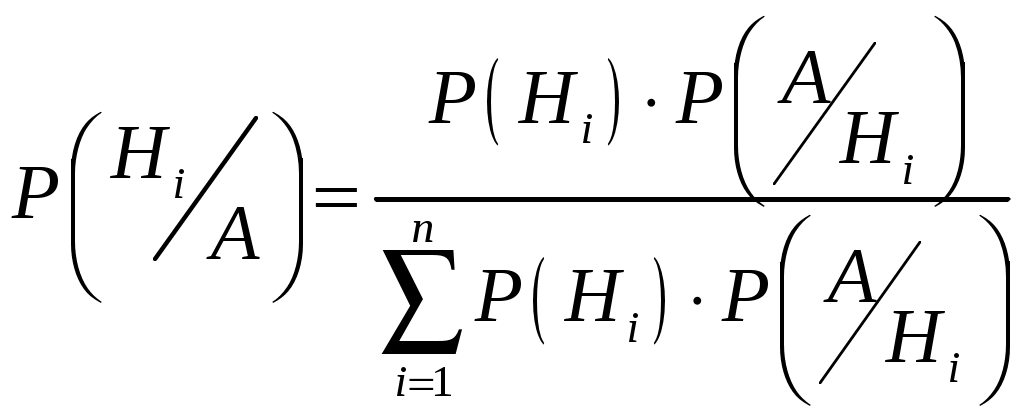 .Эта формула носит название формулы Байеса. Формула Байеса находится в тесной связи с формулой полной вероятности. Она относится к той же ситуации: событие А может наступить только с одной из гипотез Н1, Н2,…, Нn. Формула Бернулли На практике часто приходится встречаться с задачами, в которых один и тот же опыт повторяется неоднократно. В результате каждого опыта может появиться или не появиться событие А, причем нас интересует не результат каждого отдельного опыта, а общее число появлений события А в результате серии опытов. Например, производится серия выстрелов в мишень. Нас интересует не результат каждого выстрела, а общее число попаданий (или промахов). В таких задачах требуется уметь определить вероятность любого заданного числа появления события в результате серии опытов. Несколько опытов называются независимыми, если вероятность того или иного исхода каждого из опытов не зависит от того, какие исходы имели другие опыты. Например, несколько выстрелов представляют собой независимые опыты, если прицеливание производится заново перед каждым выстрелом, в противном случае выстрелы представляют собой зависимые опыты (например, стрельба очередью). Независимые опыты могут производиться в одинаковых или различных условиях. В первом случае вероятность события А во всех опытах одна и та же. Во втором случае – меняется от опыта к опыту. Если независимые опыты производятся в одинаковых условиях, то задача нахождения вероятности решается с помощью формулы Бернулли. Теорема. Если производится nнезависимых опытов, в каждом из которых событие А появляется с вероятностью р, то вероятность того, что событие А появится ровно m раз из n, выражается формулой:  , где  .Полученная формула носит название формулы Бернулли. Формула Бернулли имеет в теории вероятностей широкое применение. При выборе данной формулы необходимо обращать внимание на следующее: Производится серия n повторных независимых испытаний (опытов). Вероятность появления события не меняется от опыта к опыту и равна р. Необходимо найти вероятность того, что событие появится m раз из n. Замечание. Формула Бернулли также применяется при нахождении вероятности того, что событие появится более m раз, менее m раз, не более m раз, не менее m раз. В этих случаях применяется теорема сложения вероятностей, найденых с помощью формулы Бернулли. 2.6. Примеры решения задач к главе 2 Пример 2.1. Вероятность попадания в цель при одном выстреле равна 0,25. Найти вероятность промаха. Решение. Событие А – попадание в цель при одном выстреле. Событие  – промах при одном выстреле.Попадание и промах – события противоположные, а вероятность противоположного события  , т.е. , где  ,  .Итак,  .Пример 2.2. Вероятность того, что стрелок, произведя выстрел по мишени, выбьет 10 очков равна 0,4; 9 очков – 0,3, 8 или меньше очков – 0,3. Найти вероятность того, что стрелок при одном выстреле выбьет не менее 9 очков. Решение. Рассмотрим события: А – стрелок выбьет не менее 9 очков, А1 – стрелок выбьет 10 очков, А2 – стрелок выбьет 9 очков, А3 – стрелок выбьет 8 очков или меньше. Очевидно, что  . По теореме сложения вероятностей: , т.е.  .Можно решить задачу другим способом. Очевидно, что  , следовательно,  ;т.е.  .Пример 2.3. На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причем пять из них в переплете. Библиотекарь берет наудачу три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете. Решение. Первый способ. Событие А – хотя бы один из взятых учебников окажется в переплете. Требование «хотя бы один из трех взятых учебников в переплете» будет осуществлено, если произойдет любое из следующих несовместных событий: В – один учебник в переплете, С – два учебника в переплете, D – три учебника в переплете. Событие А можно представить в виде суммы событий: А = B + C + D. По теореме сложения, Р(А)=Р(В)+Р(С)+Р(D). Найдем вероятности событий В, С и D (см. гл. 1. § 1.5 и решение задач 1.5 – 1.8): 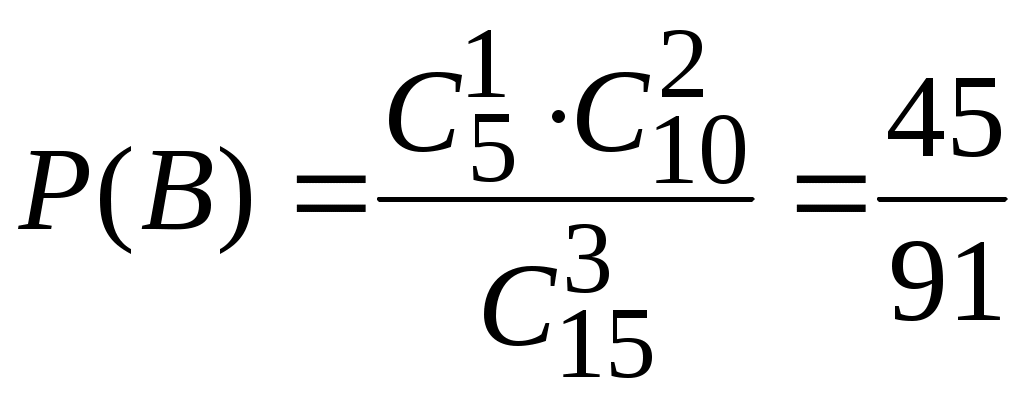 ;  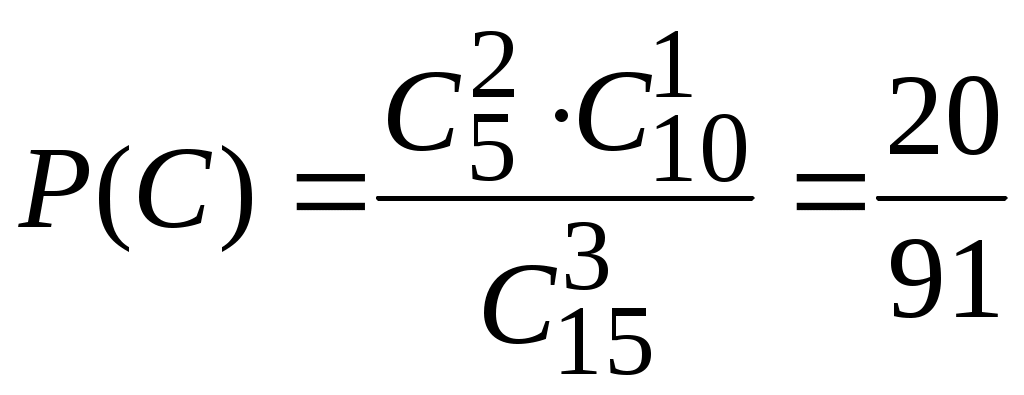;  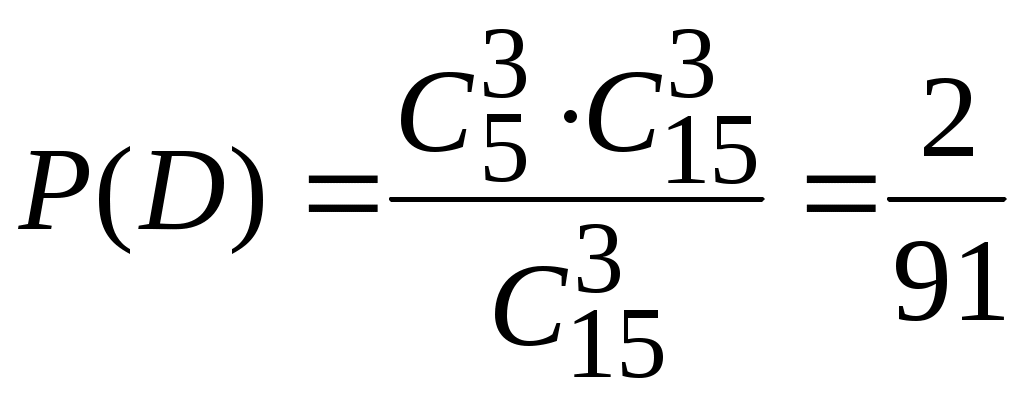.Подставив эти вероятности в равенство для Р(А), получим:  .Второй способ. События А – хотя бы один из взятых трех учебников имеет переплет и – ни один из взятых учебников не имеет переплета – противоположные, поэтому  (сумма вероятностей двух противоположных событий равна единице).Отсюда  . Вероятность появления события 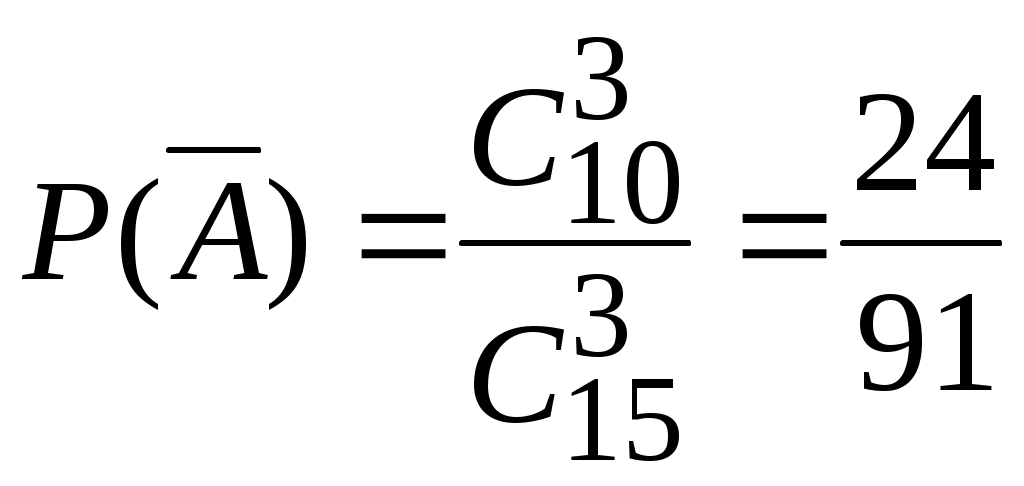:  .Тогда искомая вероятность:  .Пример 2.4. Студент делает два выстрела в мишень. Вероятность попадания при первом выстреле 0,3; при втором – 0,4. Найти вероятность двух попаданий при двух выстрелах. Обозначим: А – попадание при первом выстреле, В – попадание при втором выстреле, АВ – два попадания при двух выстрелах. События А и В не зависят друг от друга, а потому по теореме умножения:  ,  . |