матан. Теория вероятностей кажется не совсем обычной математической дисциплиной, так как имеет дело с особой категорией со случайностью. Роль случая в нашей жизни, как известно, весьма значительна
 Скачать 3.15 Mb.
|
|
Глава 4. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Плотность распределения вероятностей непрерывной случайной величины Для количественной характеристики непрерывной случайной величины используется, введенная ранее функция распределения вероятностей случайной величины (или интегральная функция распределения):  .Введем еще одну функцию распределения, называемую плотностью распределения. Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения:  .Часто вместо термина «плотность распределения» используют термины «плотность вероятностей» и «дифференциальная функция». Плотность вероятности указывает на то, что случайная величина Х часто появляется в окрестности точки х при повторении опытов. Плотность распределения есть также одна из форм закона распределения. График плотности распределения случайной величины называется кривой распределения. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а, b), определяет равенством:  .Зная плотность распределения, можно найти функцию распределения  .Геометрически это площадь фигуры, ограниченной кривой распределения и осью абсцисс левее х. 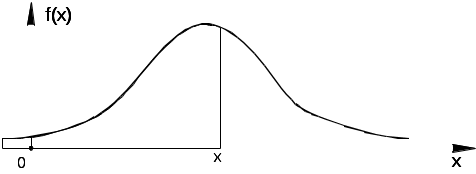 Свойства плотности распределения Плотность распределения  обладает следующими свойствами:Свойство 1. Плотность распределения неотрицательна, т.е.  .Свойство 2.Несобственный интеграл от плотности распределения в пределах от -∞ до ∞ равен единице:  .Данное условие принято называть условием нормировки непрерывной случайной величины. В частности, если все возможные значения случайной величины принадлежат интервалу (a, b), то  .Геометрически это означает, что вся площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице. Числовые характеристики непрерывной случайной величины Математическое ожидание непрерывной случайной величины Х,  ,где f(х) – плотность распределения случайной величины Х.  .Если математическое ожидание М(Х) существует и кривая распределения симметрична относительно прямой х=С, то М(Х)=С. Модой  непрерывной случайной величины Х называют то ее возможное значение, которому соответствует локальный максимум плотности распределения. В частности, если распределение имеет два одинаковых максимума, то его называют бимодальным.Медианой  непрерывной случайной величины Х называют то ее возможное значение, которое определяется равенством Геометрически медиану можно истолковать как точку, в которой ордината f(x) делит пополам площадь, ограниченную кривой распределения. Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством  или равносильным равенством  .На практике удобнее использовать последнее равенство. В частности, если все возможные значения Х принадлежат интервалу (a, b), то  или  Среднее квадратическое отклонение непрерывной случайной величины определяется так же, как и для дискетной величины:  .Все свойства дисперсии и среднего квадратического отклонения, указанные выше для дискретных случайных величин, сохраняются и для непрерывных величин. Если Y=φ(X) – функция случайного аргумента Х, причем возможные значения Х принадлежат всей оси Ох, то  или  В частности, если все возможные значения Х принадлежат интервалу (a, b), то  или  .Основные распределения непрерывной случайной величины Равномерное распределение Непрерывную случайную величину Х называют равномерно распределенной на отрезке [a, b], которому принадлежат все возможные значения Х, если ее плотность на этом отрезке постоянна и равна  .Плотность равномерно распределенной случайной величины имеет вид: 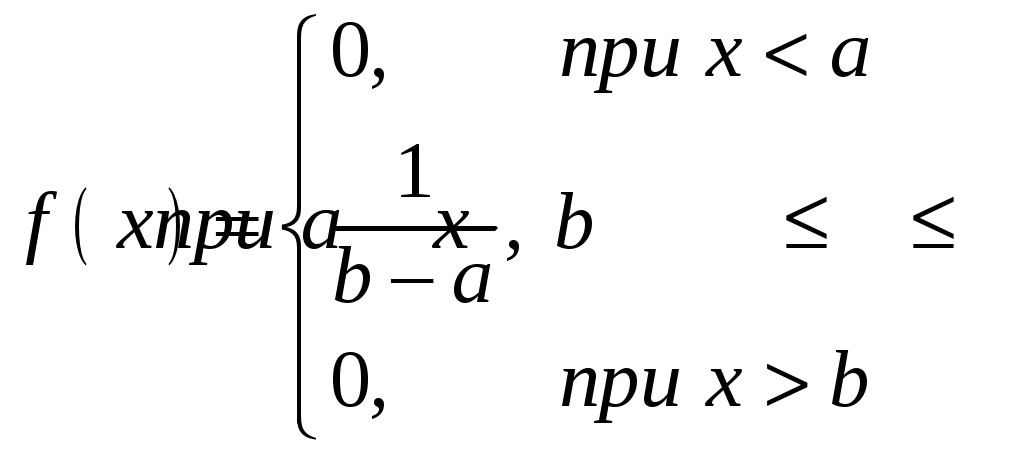 Закону равномерного распределения подчиняется, например, погрешность при измерениях с округлением или положение объекта в некоторой области, если ни одному из возможных положений нельзя отдать предпочтение. Найдем интегральную функцию равномерного распределения: 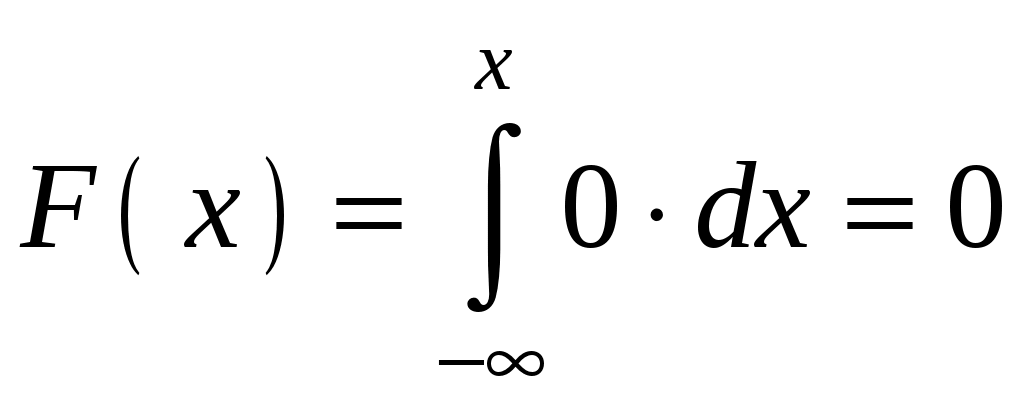  ;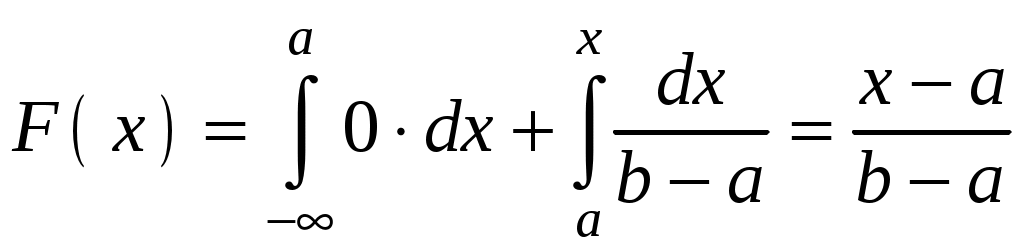  ;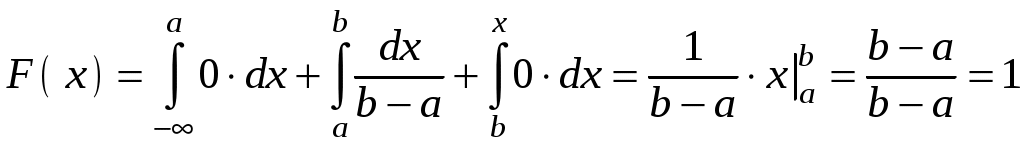  Итак, интегральная функция равномерного распределения имеет вид: 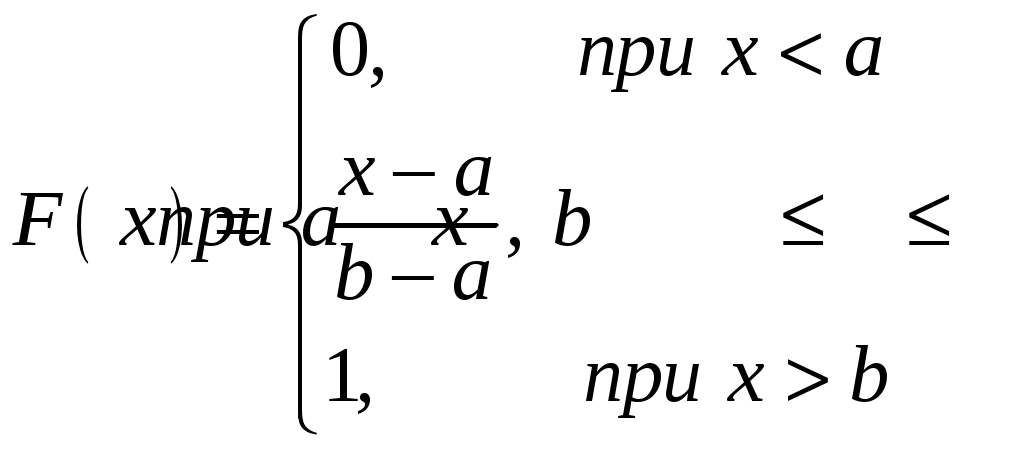 Найдем числовые характеристики равномерного распределения случайной величины: 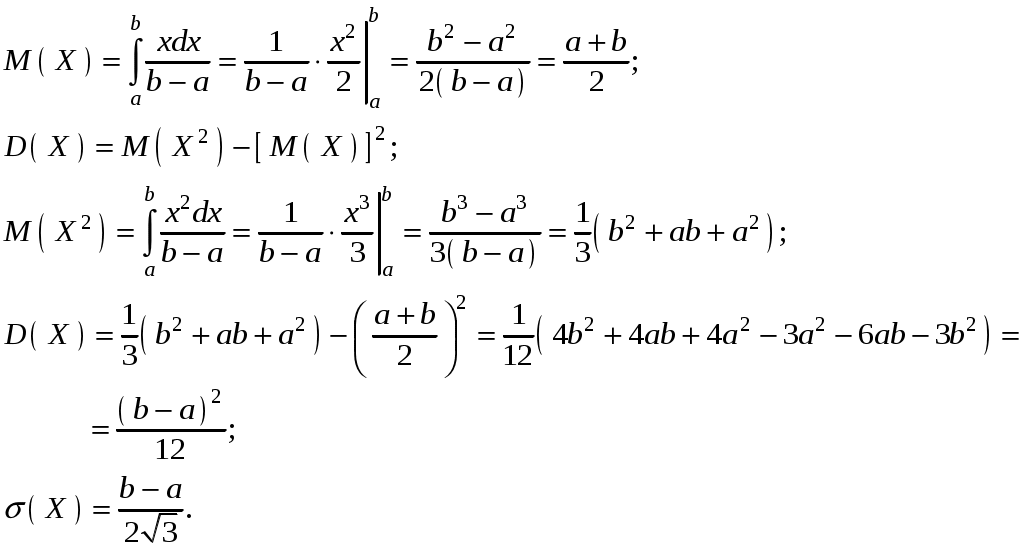 Показательное распределение Непрерывную случайную величину называют распределенной по показательному закону, если она задана дифференциальной функцией распределения: 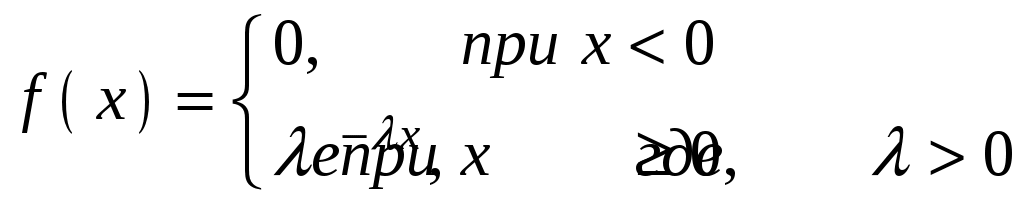 .Найдем интегральную функцию распределения: 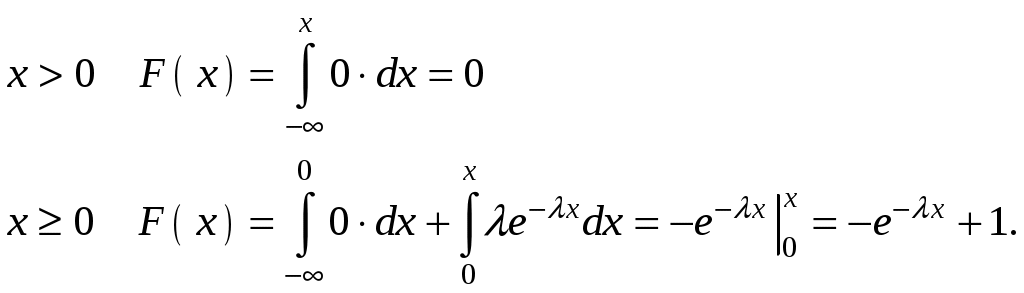 Итак, интегральная функция показательного распределения имеет вид: 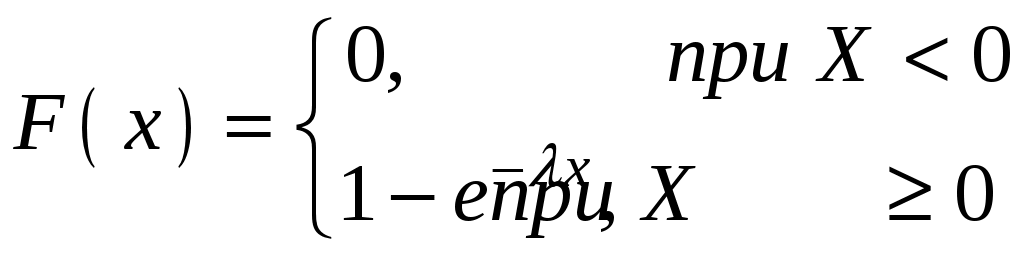 Найдем численные характеристики случайной величины, подчиненной показательному закону распределения. 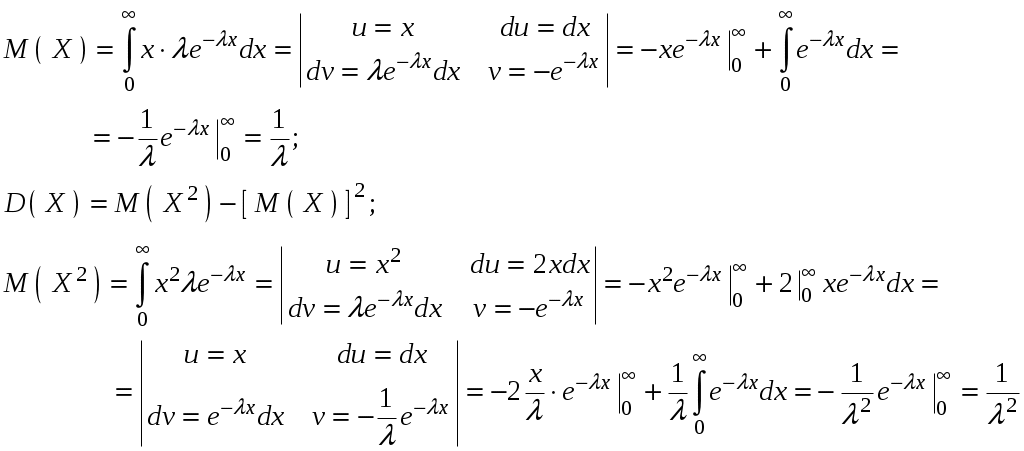  .Показательное распределение имеет случайную величину Т – длительность времени безотказной работы элемента. Под элементом понимают устройство независимо от того «простое» оно или «сложное» (например: электронная лампа, двигатель внутреннего сгорания и т.д.). Вероятность отказа элемента за время длительностью t определяется интегральной функцией показательного закона распределения:  ,где – интенсивность отказов, т.е. среднее число отказов в единицу времени. Функцией надежности  называют функцию, определяющую вероятность безотказной работы элемента за время t: .Нормальный закон распределения (закон Гаусса) Это наиболее часто встречающийся закон распределения при решении практических задач. Главная его особенность в том, что он является предельным законом, к которому приближаются другие законы при весьма часто встречающихся типичных условиях. Нормальным распределением называют распределение вероятностей непрерывной случайной величины Х, плотность которого имеет вид 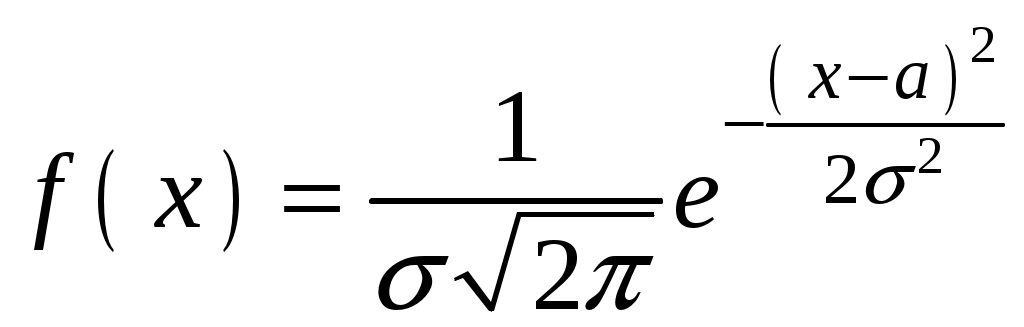 ,где a – математическое ожидание, σ – среднее квадратическое отклонение Х. Нормальный закон распределения часто называют законом Гаусса. Функция  определена при любых значениях х.Кривая нормального распределения симметрична относительно прямой 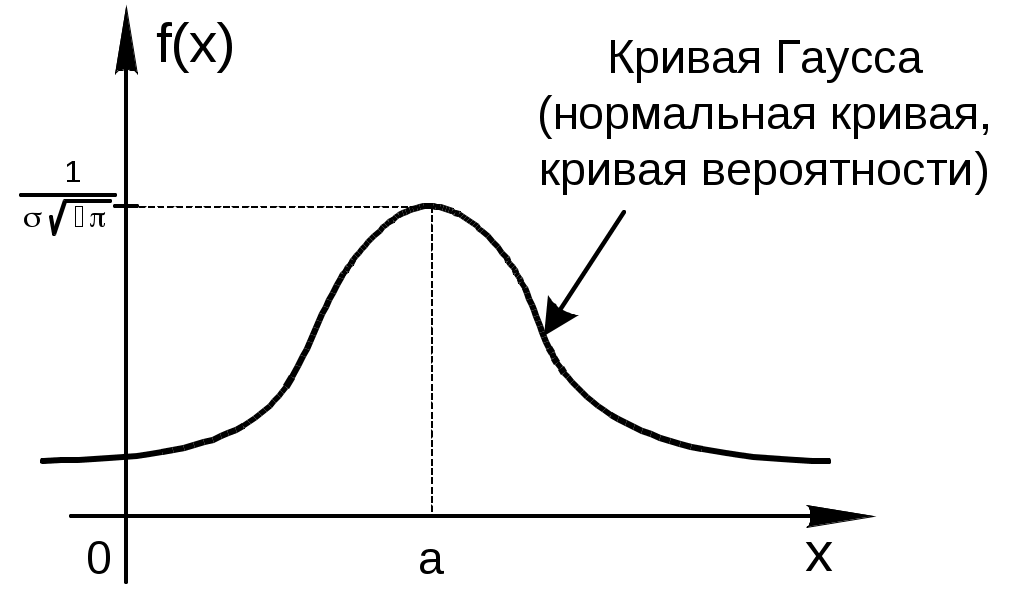 , асимптотически приближается к оси абсцисс, так как  .При функция имеет максимальное значение, а именно: . Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок равна: 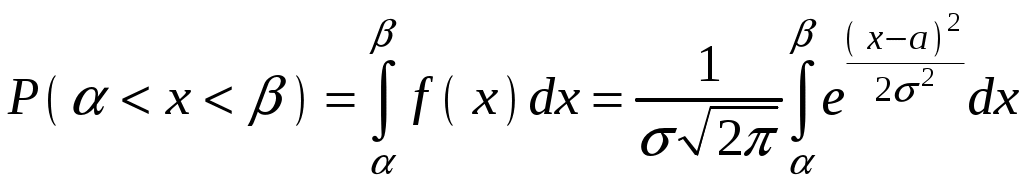 .Пользуясь заменой переменных 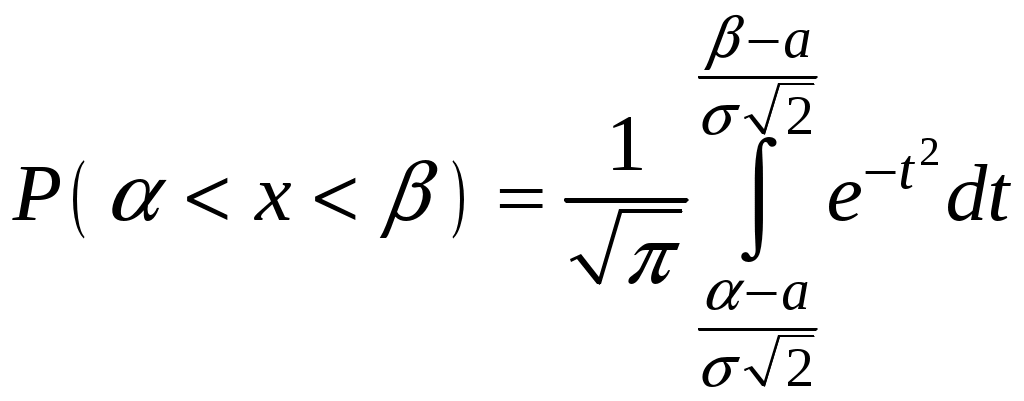 , получим: .Для нахождения этого интеграла пользуются таблицей значений функции Лапласа (или интеграла вероятностей): 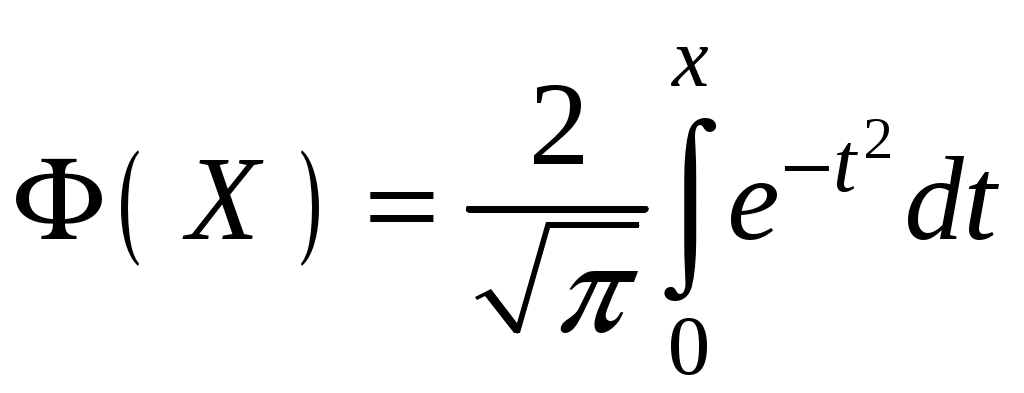 .С помощью этой функции вероятность попадания случайной величины на заданный участок 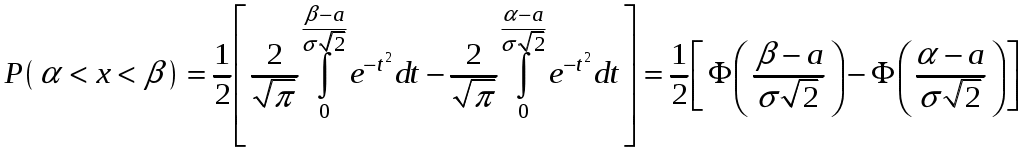 запишется следующим образом:  .Свойства функции Лапласа  ; ;Функция Лапласа есть функция нечетная, т.е.  .Замечание.  .Вычислим вероятность попадания случайной величины Х на участок длины 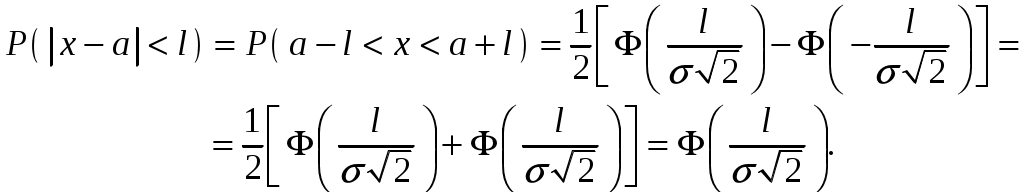 , симметричный относительно центра рассеивания а, т.е. математического ожидания.  .С помощью функции Лапласа интегральная функция распределения  выражается следующим образом:  .Асимметрия, эксцесс, мода и медиана нормального распределения соответственно равны:  где  4.4. Примеры решения задач к главе 4 Пример 4.1. Случайная величина X задана функцией распределения 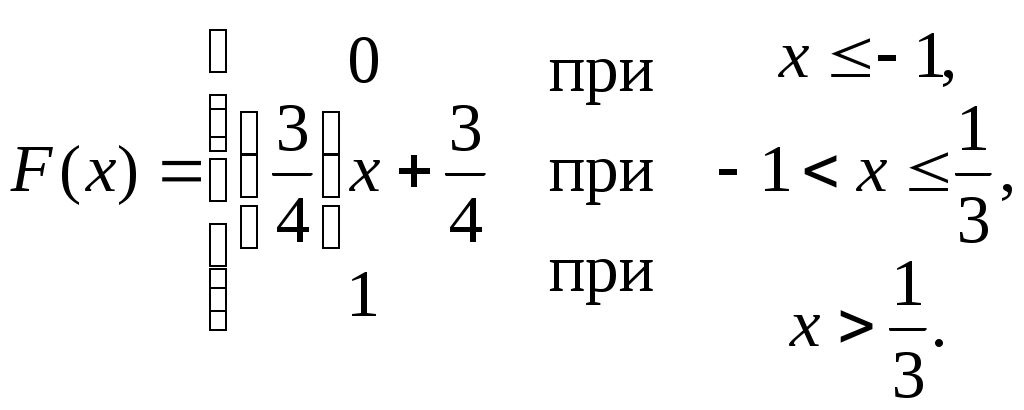 Найти вероятность того, что в результате испытания величина X примет значение, заключенное в интервале (0,  ).Решение. Вероятность того, что X примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале:  .Положив a=0, b= 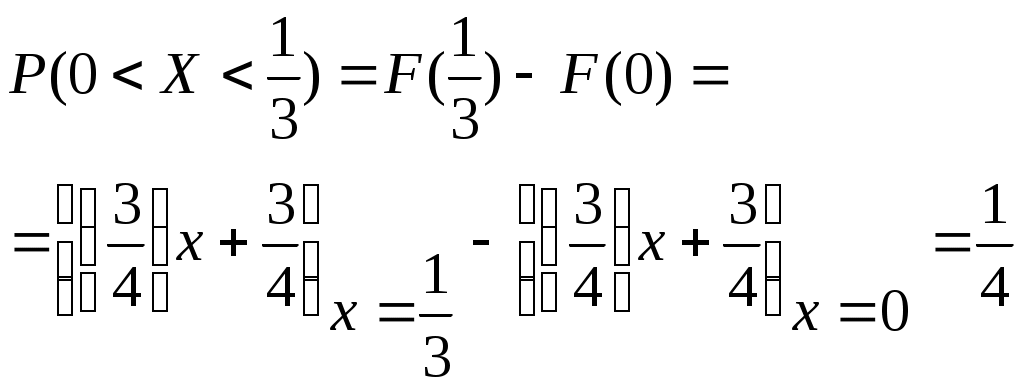, получим Пример 4.2. Случайная величина X задана функцией распределения 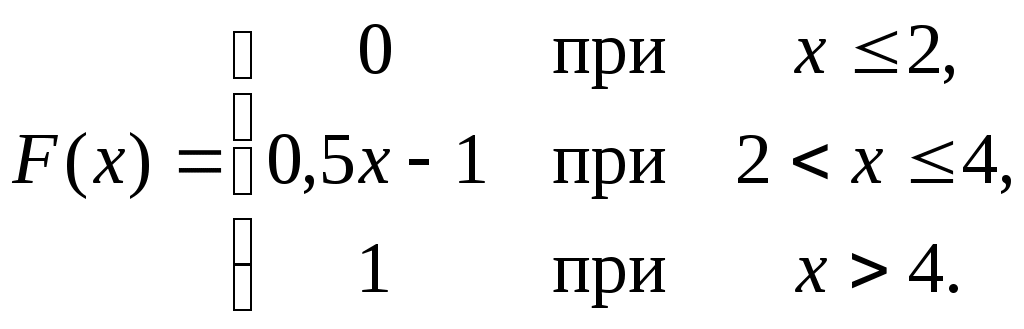 Найти вероятность того, что в результате испытания X примет значение: a) меньшее 0,2; б) меньшее трех; в) не меньше трех; г) не меньше пяти. Решение. а) Так как при  функция F(x)=0, то F(0, 2)=0, т.е. P(X<0,2)=0;б)  ;в) события  и  противоположны, поэтому  . Отсюда, учитывая, что  [см. п. б], получим ;г) сумма вероятностей противоположных событий равна единице, поэтому  .Отсюда, используя условие, в силу которого при x>4 функция F(x)=1, получим  . |