матан. Теория вероятностей кажется не совсем обычной математической дисциплиной, так как имеет дело с особой категорией со случайностью. Роль случая в нашей жизни, как известно, весьма значительна
 Скачать 3.15 Mb.
|
|
Пример 2.21. Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй – 84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом. Решение. Обозначим через А событие – деталь отличного качества. Гипотезы: Н1–деталь произведена первым автоматом, причем (поскольку первый автомат производит вдвое больше деталей, чем второй)  ;Н2 –деталь произведена вторым автоматом, причем  .Условная вероятность того, что деталь будет отличного качества, если она произведена первым автоматом,  .Условная вероятность того, что деталь будет отличного качества, если она произведена вторым автоматом,  .Вероятность того, что наудачу взятая деталь окажется отличного качества, по формуле полной вероятности равна:  .Искомая вероятность того, что взятая отличная деталь произведена первым автоматом, по формуле Байеса равна: 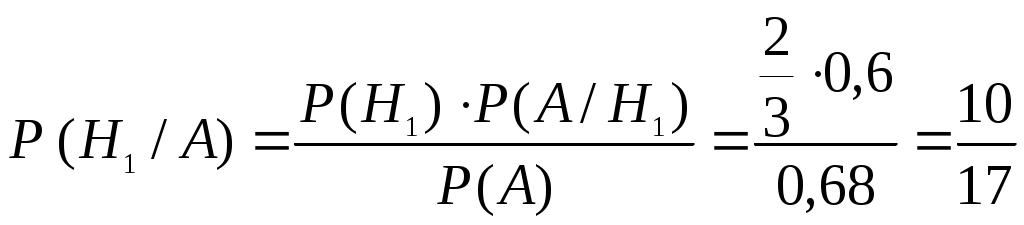 .Пример 2.22. Имеются три партии деталей по 20 деталей в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равно 20, 15, 10. Из наудачу выбранной партии наудачу извлечена деталь, оказавшаяся стандартной. Деталь возвращают в партию и вторично из той же партии наудачу извлекают деталь, которая также оказывается стандартной. Найти вероятность того, что детали были извлечены из третьей партии. Решение. Обозначим через А событие – в каждом из двух испытаний (с возвращением) была извлечена стандартная деталь. Гипотезы:  –детали извлекались из первой партии;Н2–детали извлекались из второй партии; Н3– детали извлекались из третьей партии. Детали извлекались из наудачу взятой партии, поэтому вероятности гипотез одинаковы:  .Найдем условную вероятность  , т.е. вероятность того, что из первой партии будут последовательно извлечены две стандартные детали. Это событие достоверно, так как в первой партии все детали стандартны, поэтому  .Найдем условную вероятность  , т.е. вероятность того, что из второй партии будут последовательно извлечены (с возвращением) две стандартные детали: .Найдем условную вероятность  , т.е. вероятность того, что из третьей партии будут последовательно извлечены (с возвращением) две стандартные детали: .Искомая вероятность того, что обе извлеченные стандартные детали взяты из третьей партии, по формуле Байеса равна: 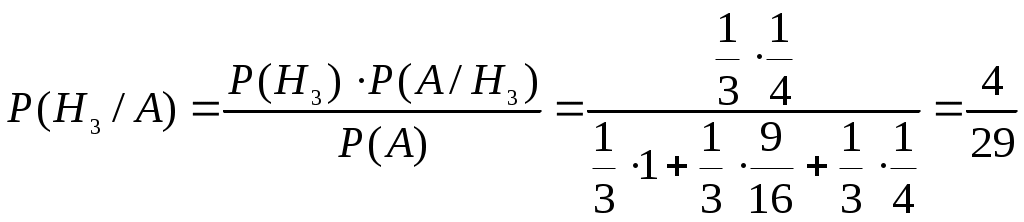 .Пример 2.23. Из 10 частных банков, работающих в городе, нарушения в уплате налогов имеют место в 6 банках. Налоговая инспекция проводит проверку трех банков, выбирая их из десяти банков случайным образом. Выбранные банки проверяются независимо один от другого. Допущенные в проверяемом банке нарушения могут быть выявлены инспекцией с вероятностью р=0,8. Какова вероятность того, что в ходе проверки будет установлен факт наличия среди частных банков города таких банков, которые допускают нарушения в уплате налогов? Решение. Событие А − в ходе проверки будет установлен факт наличия среди частных банков города таких банков, которые допускают нарушения в уплате налогов. Гипотезы: Hi − среди выбранных для проверки трех банков ровно в i банках имеют место нарушения в уплате налогов, где i=0;1;2;3. События H0, H1, H2, H3 образуют полную группу несовместных событий. Вероятность события А можно будет найти по формуле полной вероятности: 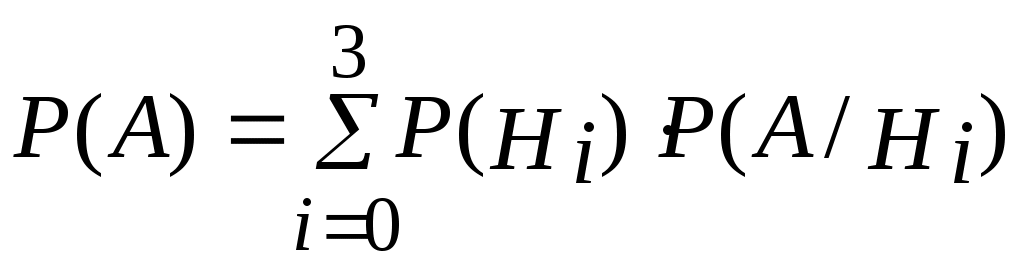 .Вычислим вероятности гипотез: 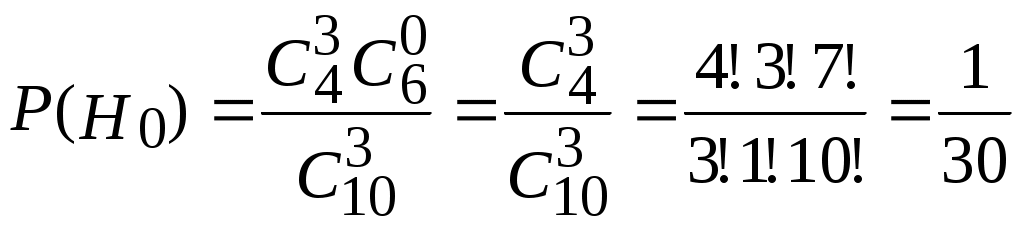 , ,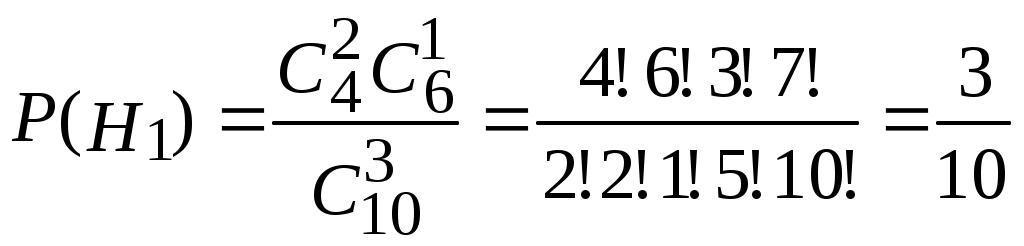 , 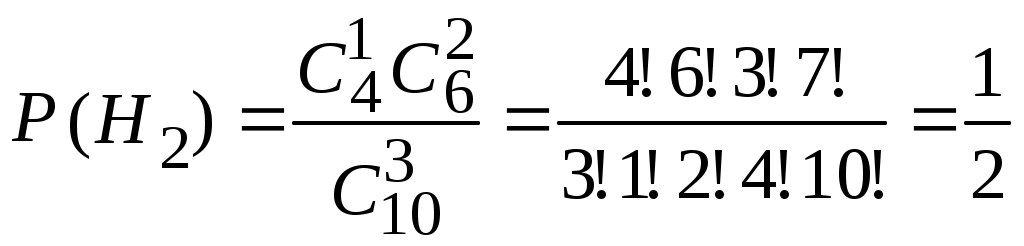  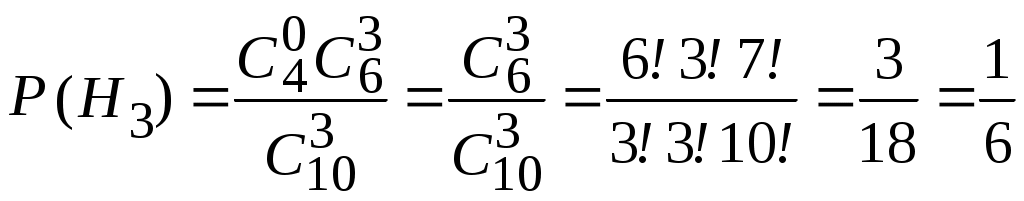.Проверим условие нормировки: 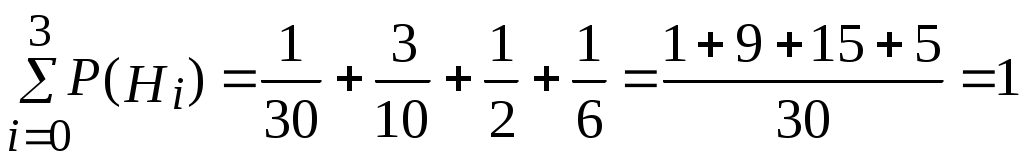 .Найдем условные вероятности события А относительно каждой гипотезы, т.е. найдем вероятности того, что нарушения в уплате налогов будут выявлены хотя бы в одном из проверяемых трех банков в каждом рассматриваемом случае. Вероятность Р(А/Hi) можно найти по формуле (т.к банки проверяются независимо один от другого) Р(А/Нi)=1−(1−р)i ,гдеi= 0;1;2;3; p=0,8.  , действительно, событие А и H0 несовместны, ; ; .Используя формулу полной вероятности, найдем  .Пример 2.24. В предыдущем примере налоговая инспекция установила факт наличия среди мастных банков города таких банков, которые допускают нарушения в уплате налогов. Найдите вероятность того, что среди случайным образом отобранных трех банков оказалось два нарушающих уплату налогов. Решение. По формуле Байеса: 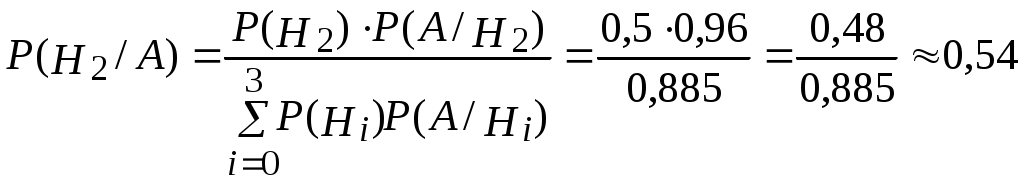 .Пример 2.25. Каждый из двух танков независимо друг от друга сделал выстрел по некоторому объекту. Вероятность попадания в цель первым танком равна 0,7; вторым – 0,6. Объект поражен одним попаданием. Определить вероятность того, что объект поражен первым танком. Решение. Событие А – поражение объекта одним попаданием. До опыта возможны следующие гипотезы: Н1 – ни один танк не попадет, Н2 – оба танка попадут, Н3 – первый танк попадет, второй – нет, Н4 – второй танк попадет, первый – нет. Вероятность этих гипотез:  ,  , ,  .Условные вероятности события А при этих гипотезах равны:  ,  ,  ,  .После опыта гипотезы Н1 и Н2 становятся невозможными, а вероятности гипотез Н3 и Н4 будут соответственно равны: 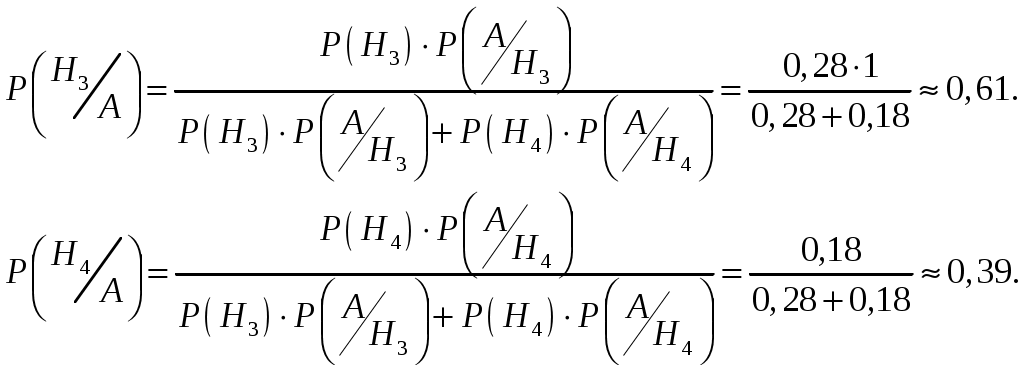 Следовательно, вероятность того, что объект поражен первым танком равна 0,61. Пример 2.26. Два из трех независимо работающих элементов вычислительного устройства отказали. Найти вероятность того, что отказали первый и второй элементы, если вероятности отказа первого, второго и третьего элементов соответственно равны 0,2; 0,4 и 0,3. Решение. Обозначим через А событие – отказали два элемента. Можно сделать следующие предположения (гипотезы):  – отказали первый и второй элементы, а третий элемент исправен, причем (поскольку элементы работают независимо, применима теорема умножения): ; – отказали первый и третий элементы, а второй элемент исправен,  ; – отказали второй и третий элементы, а первый – исправен,  – отказал только один элемент;  –отказали все три элемента;  –ни один из элементов не отказал.Вероятности последних трех гипотез не вычислены, т.к. при этих гипотезах событие А (отказали два элемента) невозможно и значит условные вероятности события А равны нулю. При гипотезах Н1, Н2,Н3событие А достоверно, поэтому соответствующие условные вероятности равны единице. По формуле полной вероятности, вероятность того, что отказали два элемента,  По формуле Байеса, искомая вероятность того, что отказали первый и второй элементы,  .Пример 2.27. В пирамиде установлено 5 винтовок, из которых 3 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с прицелом равна 0,95, для винтовки без прицела – 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки. Решение. Событие А – мишень поражена. Гипотезы: Н1 – винтовка с оптическим прицелом; Н2 – винтовка без оптического прицела. Вероятности гипотез:  ,  .Условные вероятности события А:  ,  .По формуле полной вероятности: 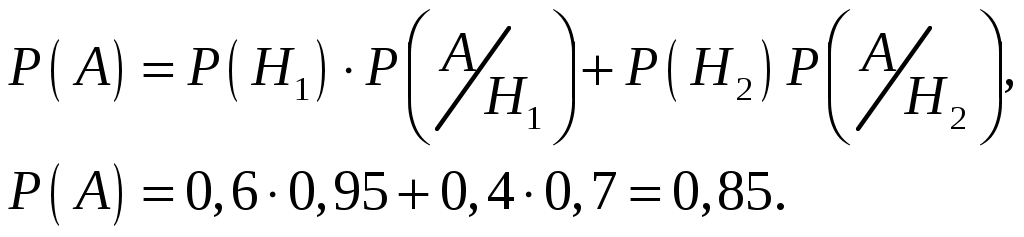 Пример 2.28. Число грузовых машин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, как 3:2. Вероятность того, что будет заправляться грузовая машина равна 0,1; для легковых машин эта вероятность равна 0,2. К бензоколонке подъехала машина для заправки. Найти вероятность того, что эта машина грузовая. Решение. А – к бензоколонке подъехала машина. Гипотезы: Н1 – машина грузовая; Н2 – машина легковая. Вероятности гипотез до опыта: ; .Условные вероятности:  ,  .По формуле Байеса: 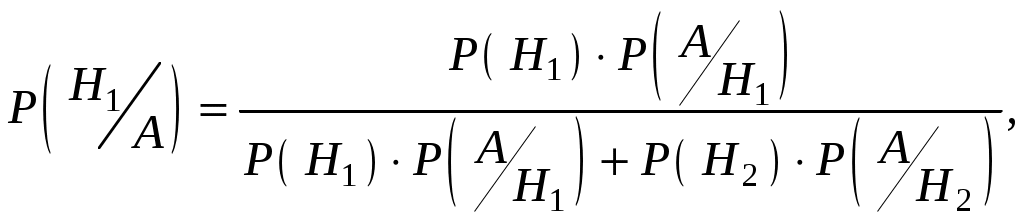  Пример 2.29. На склад поступает продукция 3-х фабрик. Причем, продукция первой фабрики составляет 20%, второй – 46% и третьей – 34%. Известно, что средний процент нестандартных изделий для первой фабрики равен 3%, для второй – 2%, для третьей – 1%. Найти вероятность того, что наудачу взятые изделия произведены на первой фабрике, если оно казалось нестандартным. Решение. А – изделие нестандартное. Гипотезы: Н1 – изделие изготовлено на первой фабрике; Н2 – изделие изготовлено на второй фабрике; Н3 – изделие изготовлено на третьей фабрике. Вероятности гипотез:  ,  ,  .Условные вероятности:  ,  ,  .По формуле Байеса: 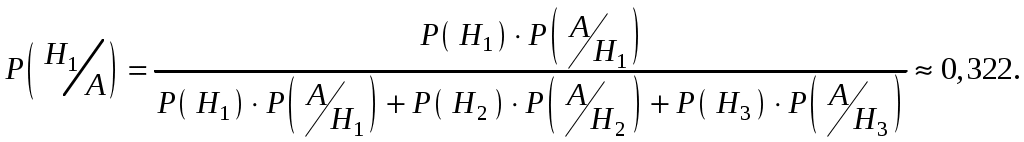 Пример 2.30. Вероятность попадания в цель при одном выстреле равна 0,4. Какова вероятность получить три попадания при пяти выстрелах? Решение. Применяем формулу Бернулли:  .По условию:  , тогда  . n=5, m=3.Подставляем в формулу:  .Пример 2.31. Вероятность того, что деталь стандартная равна 0,7. Какова вероятность того, что среди взятых наудачу 6 деталей стандартными окажутся: 4 детали; не менее 4-х деталей; не более 3-х деталей? Решение: Событие А – деталь стандартная. Применяем формулу Бернулли. По условию:  а)  ;  ;б)  ;  = ;с)  ;  +  .Пример 2.32. Вероятность хотя бы одного попадания при двух выстрелах равна 0,96. Найти вероятность трех попаданий при четырех выстрелах. Решение.  ,  . , , =>  .Применяем формулу Бернулли:  .Задания для самостоятельного решения 2.1. В ящике 10 деталей, из которых четыре окрашены. Сборщик наудачу взял три детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена. 2.2. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор. 2.3. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков. 2.4. Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,38. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,8. 2.5. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартное. 2.6. Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены три независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность. 2.7. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трех проверенных изделий только два изделия высшего сорта. 2.8. Устройство состоит из трех элементов, работающих независимо. Вероятности безотказной работы (за время t) первого, второго и третьего элементов соответственно равны 0,6; 0,7; 0,8. Найти вероятности того, что за время t безотказно будут работать: а) только один элемент; б) только два элемента; в) все три элемента. 2.9. Вероятности того, что нужная сборщику деталь находится в первом, втором, третьем, четвертом ящике, соответственно равны 0,6; 0,7; 0,8; 0,9. Найти вероятности того, что деталь содержится: а) не более чем в трех ящиках; б) не менее чем в двух ящиках. 2.10. Брошены три игральные кости. Найти вероятности следующих событий: а) на каждой из выпавших граней появится пять очков; б) на всех выпавших гранях появится одинаковое число очков. 2.11. Брошены три игральные кости. Найти вероятности следующих событий: а) на двух выпавших гранях появится одно очко, а на третьей грани – другое число очков; б) на двух выпавших гранях появится одинаковое число очков, а на третьей грани – другое число очков; в) на всех выпавших гранях появится разное число очков. 2.12. Вероятность попадания в мишень стрелком при одном выстреле равна 0,8. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью, меньшей 0,4, можно было ожидать, что не будет ни одного промаха? 2.13. В круг радиуса R вписан правильный треугольник. Внутрь круга наудачу брошены четыре точки. Найти вероятности следующих событий: а) все четыре точки попадут внутрь треугольника; б) одна точка попадет внутрь треугольника и по одной точке попадет на каждый «малый» сегмент. Предполагается, что вероятность попадания точки в фигуру пропорциональна площади фигуры и не зависит от ее расположения. 2.14. Отрезок разделен на три равные части. На этот отрезок наудачу брошены три точки. Найти вероятность того, что на каждую из трех частей отрезка попадает по одной точке. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения. 2.15. Среди 100 лотерейных билетов есть 5 выигрышных. Найти вероятность того, что 2 наудачу выбранные билета окажутся выигрышными. 2.16. В ящике 10 деталей, среди которых шесть окрашенных. Сборщик наудачу извлекает четыре детали. Найти вероятность того, что все извлеченные детали окажутся окрашенными. 2.17. В урне имеется пять шаров с номерами от 1 до 5. Наудачу по одному извлекают три шара без возвращения. Найти вероятности следующих событий: а) последовательно появятся шары с номерами 1, 4, 5; б) извлеченные шары будут иметь номера 1, 4, 5 независимо от того, в какой последовательности они появились. 2.18. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором три вопроса. 2.19. В мешочке содержится 10 одинаковых кубиков с номерами от 1 до 10. Наудачу извлекают по одному три кубика. Найти вероятность того, что последовательно появятся кубики с номерами 1, 2, 3, если кубики извлекаются: а) без возвращения; б) с возвращением (извлеченный кубик возвращается в мешочек). 2.20. Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятности отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент. 2.21. Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны: 0,3; 0,4; 0,6; 0,7. 2.22. Три исследователя, независимо один от другого, производят измерения некоторой физической величины. Вероятность того, что первый исследователь допустит ошибку при считывании показаний прибора, равна 0,1. Для второго и третьего исследователей эта вероятность соответственно равна 0,15 и 0,2. Найти вероятность того, что при однократном измерении хотя бы один из исследователей допустит ошибку 2.23. Вероятность попадания в мишень каждым из двух стрелков равна 0,3. Стрелки стреляют по очереди, причем каждый должен сделать по два выстрела. Попавший в мишень первым получает приз. Найти вероятность того, что стрелки получат приз. 2.24. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле. 2.25. В урну, содержащую п шаров, опущен белый шар, после чего наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равно возможны все возможные предположения о первоначальном составе шаров (по цвету). 2.26. В вычислительной лаборатории имеются шесть клавишных автоматов и четыре полуавтомата. Вероятность того, что за время выполнения некоторого расчета автомат не выйдет из строя, равна 0,95; для полуавтомата эта вероятность равна 0,8. Студент производит расчет на наудачу выбранной машине. Найти вероятность того, что до окончания расчета машина не выйдет из строя. 2.27. В пирамиде пять винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки. 2.28. В ящике содержатся 12 деталей, изготовленных на заводе №1, 20 деталей – на заводе №2 и 18 деталей – на заводе №3. Вероятность того, что деталь, изготовленная на заводе №1, отличного качества, равна 0,9; для деталей, изготовленных на заводах №2 и №3, эти вероятности соответственно равны 0,6 и 0,9. Найти вероятность того, что извлечение наудачу деталь окажется отличного качества 2.29. В первой урне содержится 10 шаров, из них 8 белых; во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взят один шар. Найти вероятность того, что взят белый шар. 2.30. В каждой из трех урн содержится 6 черных и 4 белых шара. Из первой урны наудачу извлечен один шар и переложен во вторую урну, после чего из второй урны наудачу извлечен один шар и переложен в третью урну. Найти вероятность того, что шар, наудачу извлеченный из третьей урны, окажется белым. 2.31. Вероятности того, что во время работы цифровой электронной машины произойдет сбой в арифметическом устройстве, в оперативной памяти, в остальных устройствах, относятся как 3:2:5, Вероятности обнаружения сбоя в арифметическом устройстве в оперативной памяти и в остальных устройствах соответственно равны 0,8; 0,9; 0,9. Найти вероятность того, что возникшей в машине сбой будет обнаружен. 2.32. В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него? 2.33. Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по тому же шоссе как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это легковая машина. 2.34. Две перфораторщицы набили на разных перфораторах по одинаковому комплекту перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,05; для второй перфораторщицы эта вероятность равна 0,1. При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошиблась первая перфораторщица. (Предполагается, что оба перфоратора были исправны.) 2.35. В специализированную больницу поступают в среднем 50% больных с заболеванием К 30% с заболеванием L, 20% с заболеванием М. Вероятность полного излечения болезни K равна 0,7; для болезней Lи М эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что этот больной страдал заболеванием K. 2.36. Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,55, а ко второму – 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, равна 0,9, а вторым – 0,98. Стандартное изделие при проверке было признано стандартным. Найти вероятность того, что это изделие проверил второй товаровед. 2.37. Два равносильных противника играют в шахматы. Что вероятнее: а) выиграть одну партию из двух или две партии из четырех? б) выиграть не менее двух партий из четырех или не менее трех партий из пяти? Ничьи во внимание не принимаются. 2.38. Монету бросают пять раз. Найти вероятность того, что «герб» выпадет: а) менее двух раз; б) не менее двух раз. 2.39. а) Найти вероятность того, что событие А появится не менее трех раз в четырех независимых испытаниях, если вероятность появления события А в одном испытании равна 0,4; б) событие В появится в случае, если событие А наступит не менее четырех раз. Найти вероятность наступления события В, если будет произведено пять независимых испытаний, в каждом из которых вероятность появления события А равна 0,8. 2.40. Устройство состоит из трех независимо работающих основных элементов. Устройство отказывает, если откажет хотя бы один элемент. Вероятность отказа каждого элемента за время t равна 0,1. Найти вероятность безотказной работы устройства за время t, если: а) работают только основные элементы; б) включен один резервный элемент; в) включены два резервных элемента. Предполагается, что резервные элементы работают в том же режиме, что и основные, вероятность отказа каждого резервного элемента также равна 0,1 и устройство отказывает, если работает менее трех элементов. 2.41. В семье пять детей. Найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков; в) более двух мальчиков; г) не менее двух и не более трех мальчиков. Вероятность рождения мальчика принять равной 0,51. 2.42. Количество панелей, поступающих на стройку с заводов №1, №2, №3 пропорционально 5:7:8; причем процент выпуска бракованных изделий с завода №1 равен 5%, с завода №2 – 4% и с завода №3 – 2%. Какова вероятность того, что случайно выбранная панель содержит брак? 2.43. Для некоторой местности число дождливых дней в августе равно 11. Чему равна вероятность того, что первые три дня августа а) будут дождливыми, б) будут не дождливыми? 2.44. Сборщик получил 3 ящика деталей: в первом ящике 40 деталей, из них 20 окрашенных; во втором. 50, из них 10 окрашенных; в третьем – 30 деталей, из них 15 окрашенных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика окажется окрашенной. 2.45. Рабочий обслуживает 5 станков, каждый из которых за смену может потребовать внимание рабочего с вероятностью 0,25. Найти вероятность того, что за смену не менее двух станков потребуют внимания рабочего. 2.46. Вероятность того, что каждый из трех друзей придет в условленное место, соответственно равны 0,8; 0,6; 0,7. Определить вероятность того, что встреча состоится, если для этого достаточно явиться двум из трех друзей. 2.47. На двух станках обрабатываются однотипные детали; вероятность брака для станка №1 составляет 0,03, а для станка №2 – 0,02. Обработанные детали складываются в одном месте, причем деталей со станка №1 складывается вдвое больше, чем со станка №2. Вычислить вероятность того, что взятая наудачу, оказавшаяся не бракованной деталь, была обработана на станке №1. 2.48. Фирма имеет три источника поставки комплектующих. фирмы А, В, С. на долю фирмы А приходится 50% общего объема поставок, В – 30% и С – 20%. Из практики известно, что 10% поставляемых фирмой А деталей бракованные, фирмой В – 5% си фирмой С – 6%. Какова вероятность, что взятая наугад и оказавшаяся бракованной деталь получена от фирмы А? 2.49. На станции отправления имеется 8 заказов на отправку товара: пять – внутри страны, а три – на экспорт. Какова вероятность того, что два выбранных наугад заказа окажутся предназначенными 1) для потребления внутри страны, 2) на экспорт, 3) один из них для потребления внутри страны, другой на экспорт? 2.50. Совет директоров состоит из трех бухгалтеров, трех менеджеров и двух инженеров. Планируется создать подкомитет из его членов. Какова вероятность того, что все трое в этом подкомитете будут бухгалтеры? 2.51. В центральную бухгалтерию поступили пачки накладных для проверки и обработки. 90% пачек были признаны удовлетворительными: они содержали только 1 % неправильно оформленных накладных. Остальные 10% пачек накладных были признаны неудовлетворительными, т.к. содержали 5% неправильно оформленных накладных. Взятая наугад из пачки накладная оказалась оформленной неправильно. Учитывая это, какова вероятность того, что вся пачка накладных будет признана несоответствующей стандартам? 2.52. На складе находятся 6 костюмов 48 размера, 10 костюмов 50 размера и 8 костюмов 52 размера. Случайным образом выбирают 2 костюма. Найти вероятностьтого, что они окажутся 1) одного размера, 2) разных размеров. 2.53. Первый магазин может выполнить план с вероятностью 0,9, второй с вероятностью 0,8, а третий – с вероятностью 0,7. Найти вероятность того, что план выполнят: а) не менее двух магазинов, б) не более одного магазина. 2.54. Студент знает 30 вопросов из 40. Ему наудачу заданы 2 вопроса. Какова вероятность того, что он ответит а) на оба вопроса, б) хотя бы на один из них? 2.55. Первый товаровед проверяет 40% всех изделий и в 9% случаев обнаруживает имеющийся брак. Второй товаровед проверяет всю остальную продукцию, но брак обнаруживает только в 95% случаев. Бракованное изделие оказалось бракованным. Какова вероятность того, что его проверял первый товаровед? 2.56. В заводскую столовую вошли рабочий, бухгалтер и сотрудник планового отдела. Известно, что соответствующие категории работников завода пользуются буфетом при столовой с вероятностью 0,6; 0,8; 0,9. Какова вероятность того, что буфетом воспользуются а) только двое из вошедших, б) хотя бы один из вошедших? 2.57. На контроль поступают одинаковые блюда, изготовленные двумя поварами. Производительность первого повара вдвое больше, чем второго. Процент брака у первого повара 0,8%, у второго – 0,6%. Проверяемое блюдо не удовлетворяет требованиям контроля. Найти вероятность того, что оно изготовлено вторым поваром. Часть II. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ |