матан. Теория вероятностей кажется не совсем обычной математической дисциплиной, так как имеет дело с особой категорией со случайностью. Роль случая в нашей жизни, как известно, весьма значительна
 Скачать 3.15 Mb. Скачать 3.15 Mb.
|
|
Найти функцию распределения F(х) и начертить ее график. Решение. 1. Если х≤2, то F(х)=0. Действительно, значений, меньших числа 2, величина Х не принимает. Следовательно, при х≤2 функция F(х)=Р(Х<x)=0. 2. Если 2 Действительно, Х может принять значение 2 с вероятностью 0,5. 3. Если 4<х≤7, то F(х)=0,7. Действительно, Х может принять значение 2 с вероятностью 0,5 и значение 4 с вероятностью 0,2; следовательно, одно из этих значений, безразлично какое, Х может принять (по теореме сложения вероятностей несовместных событий) с вероятностью 0,5+0,2=0,7. 4. Если х>7, то F(х)=1. Действительно, событие Х≤7 достоверно и вероятность его равна единице. Итак, искомая функция распределения имеет вид 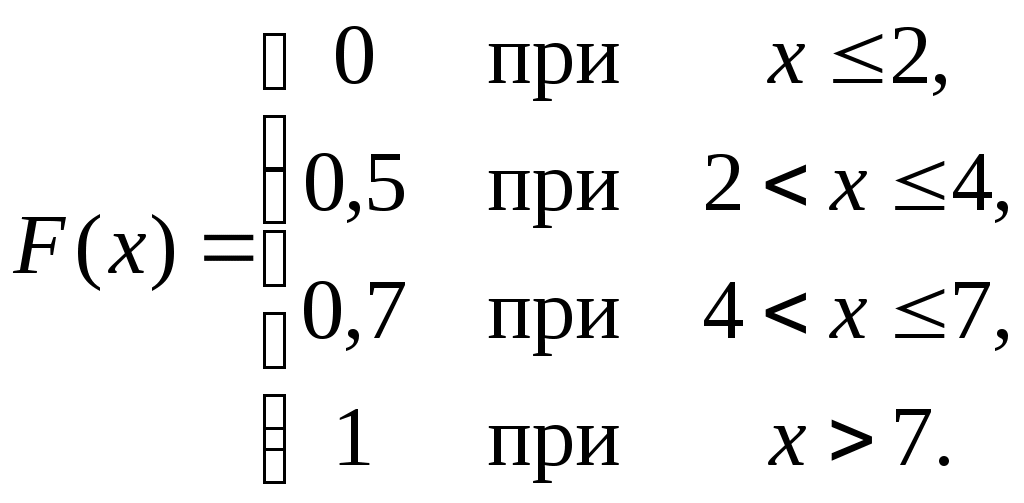 График этой функции: 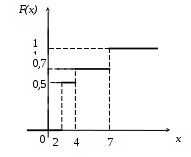 Пример 4.7. Дана интегральная функция случайной величины Х: 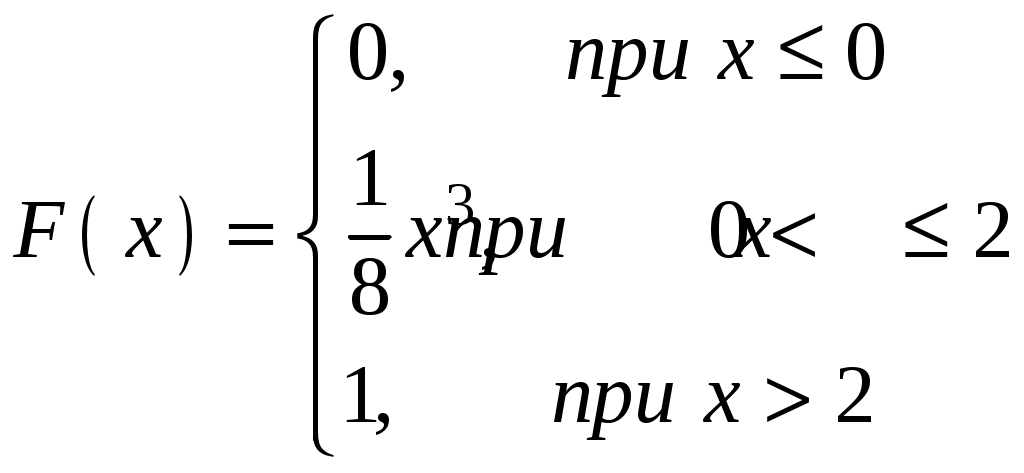 Найти плотность вероятности, построить ее график и найти вероятность того, что в результате испытания случайная величина Х примет значение в интервале (0,5; 1,5). Решение. 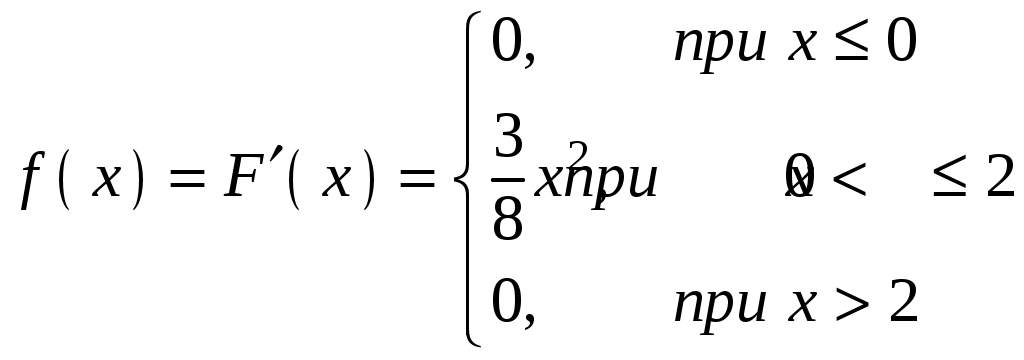 График этой функции: 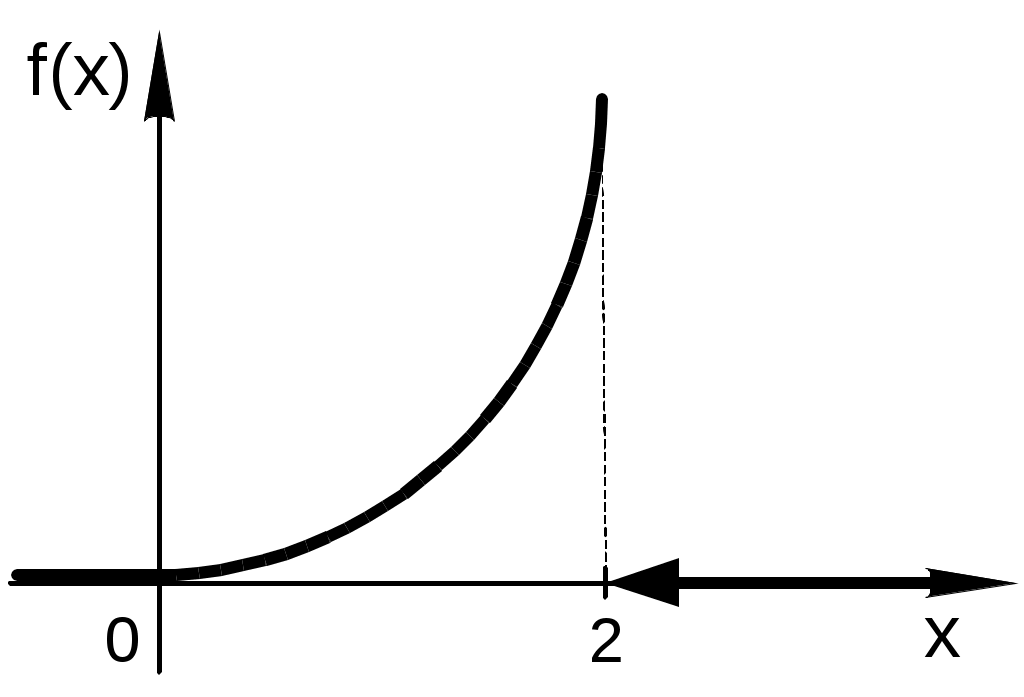 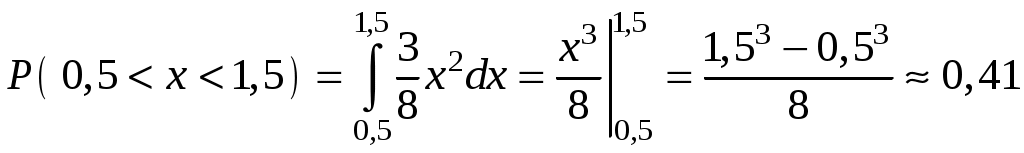 Пример 4.8. Случайная величина Х задана плотностью распределения: 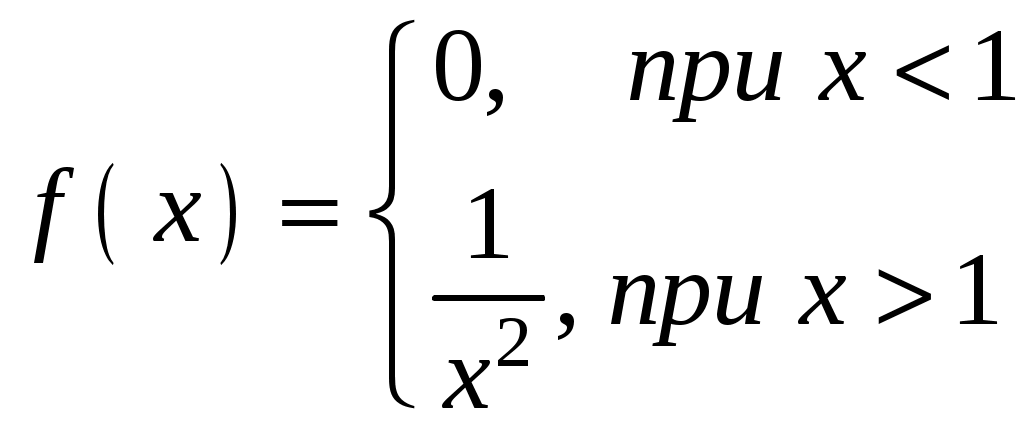 Построить график дифференциальной и интегральной функции распределения. Решение. 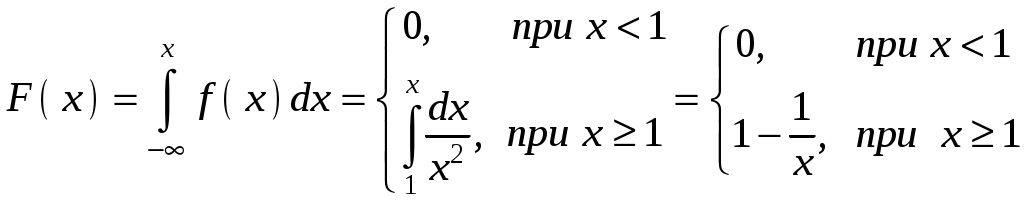 . .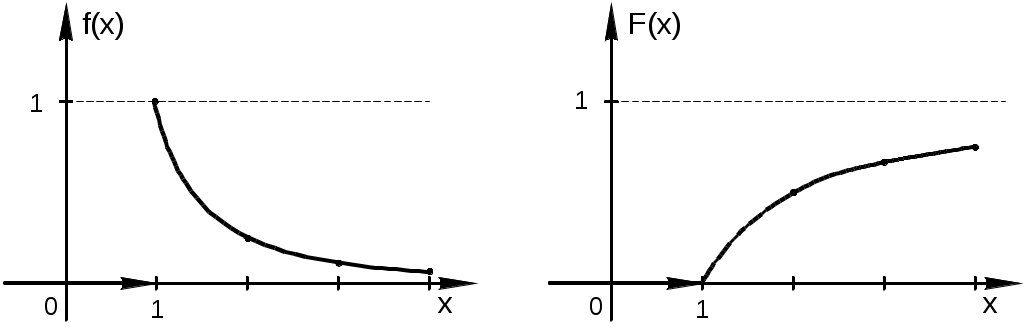 Пример 4.9. Дана функция распределения непрерывной случайной величины Х: 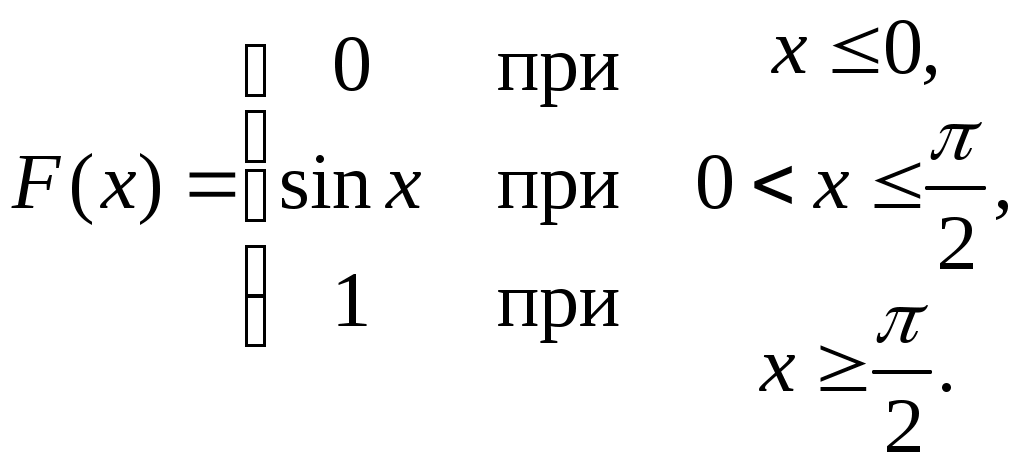 Найти плотность распределения f(х). Решение. Плотность распределения равна первой производной от функции распределения: 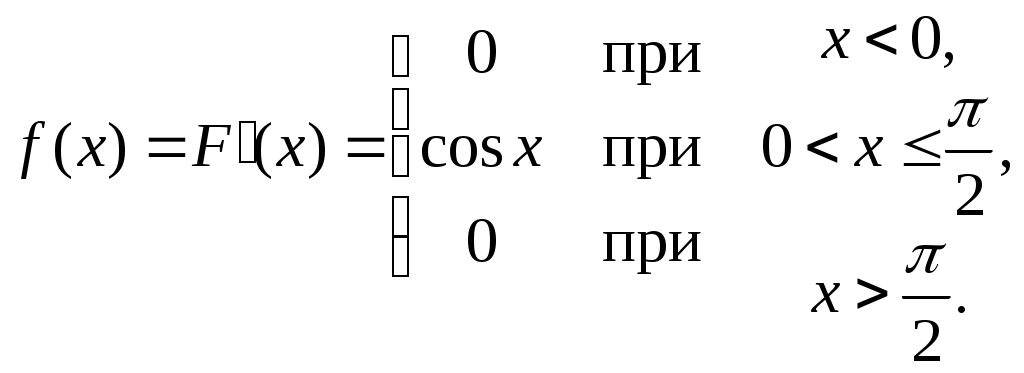 Заметим, что при х=0 производная Пример 4.10. Непрерывная случайная величина Х задана плотностью распределения Найти вероятность того, что Х примет значение, принадлежащее интервалу ( Решение. Воспользуемся формулой По условию, Следовательно, искомая вероятность Пример 4.11. Задана плотность распределения непрерывной случайной величины Х: 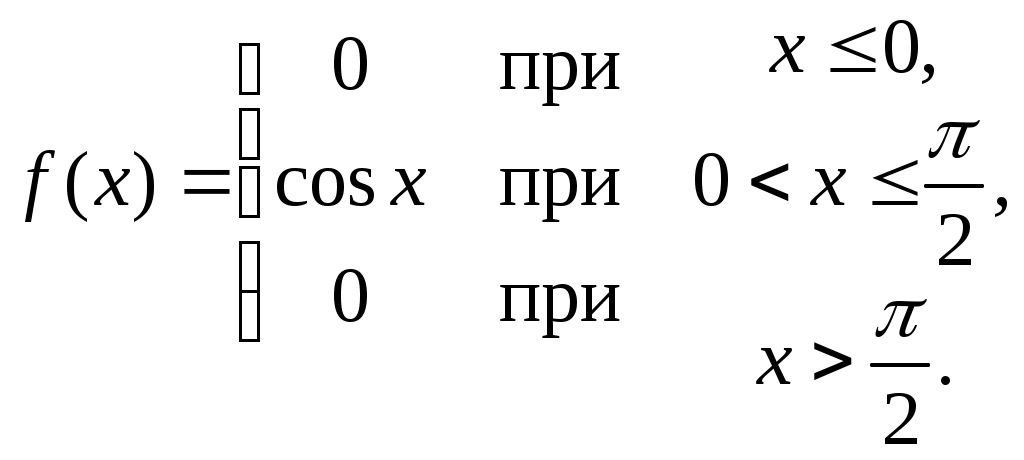 Найти функцию распределения F(x). Решение. Используем формулу Если х≤0, то f(х)=0, следовательно, Если Если Итак, искомая функция распределения 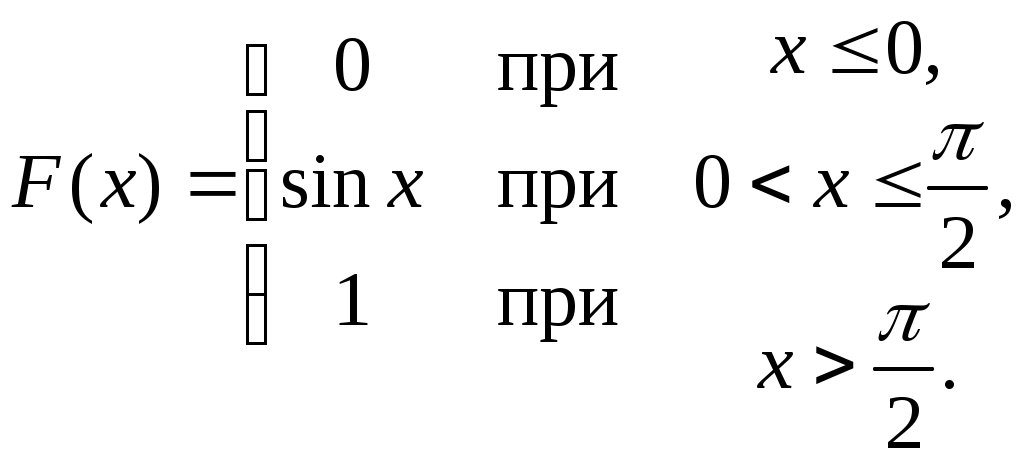 Пример 4.12. Найти дисперсию и среднее квадратичное отклонение случайной величины Х, если: 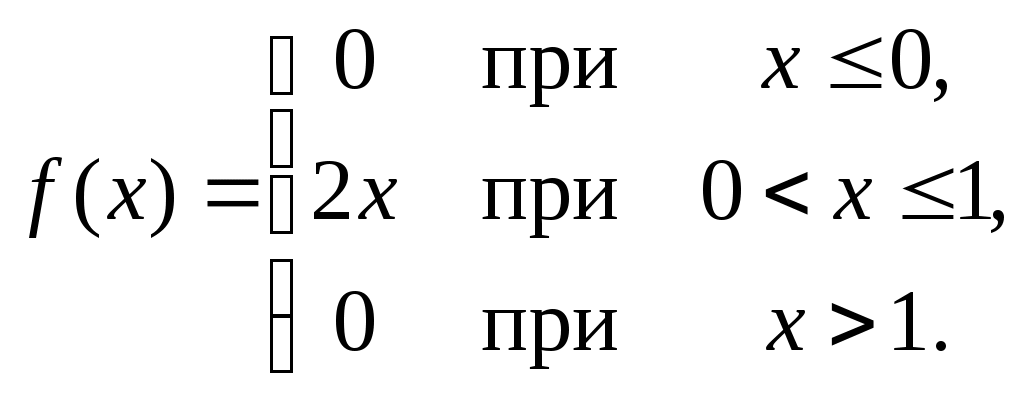 Решение. Используем формулу Подставив а=0, b=1, f(х)=2х, получим Дисперсию можно вычислить, пользуясь формулой: 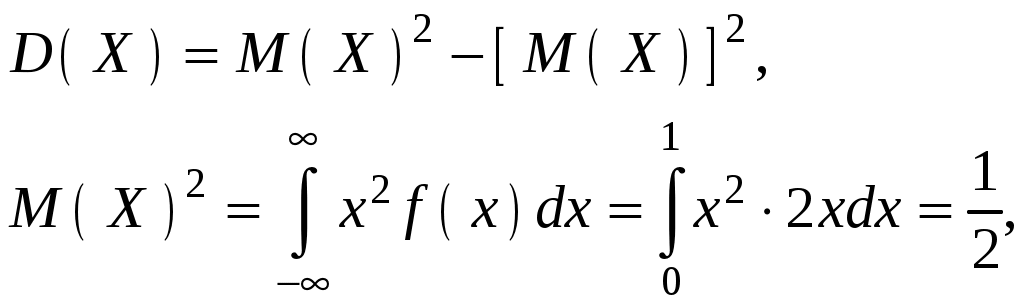 тогда 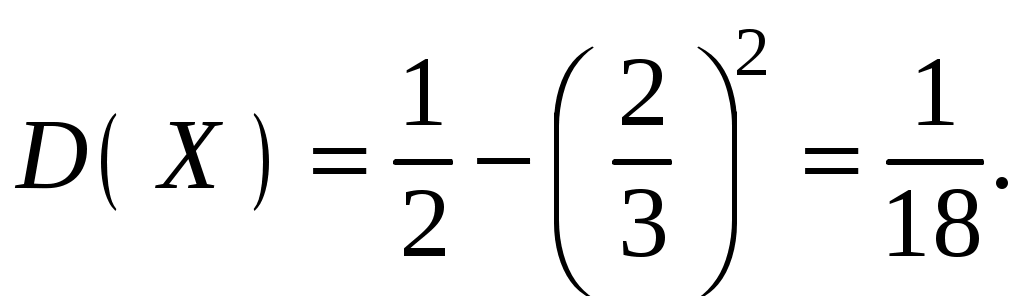 Пример 4.13. Найти математическое ожидание случайной величины Х, заданной функцией распределения 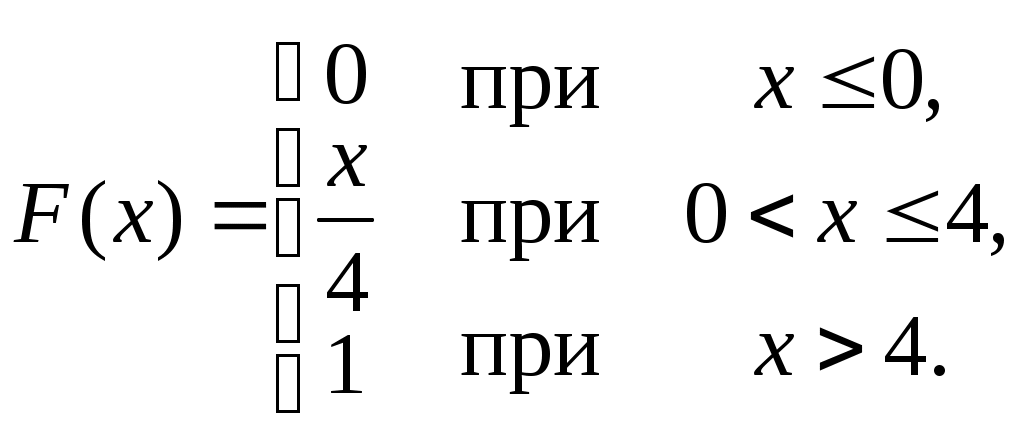 Решение. Найдем плотность распределения величины Х: 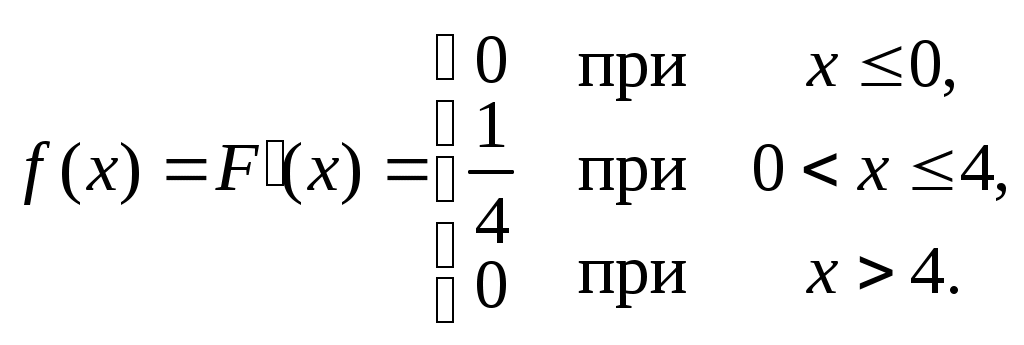 Найдем искомое математическое ожидание: Пример 4.14. Случайная величина X − годовой доход наугад взятого лица, облагаемого налогом. Плотность распределения этой случайной величины имеет вид: 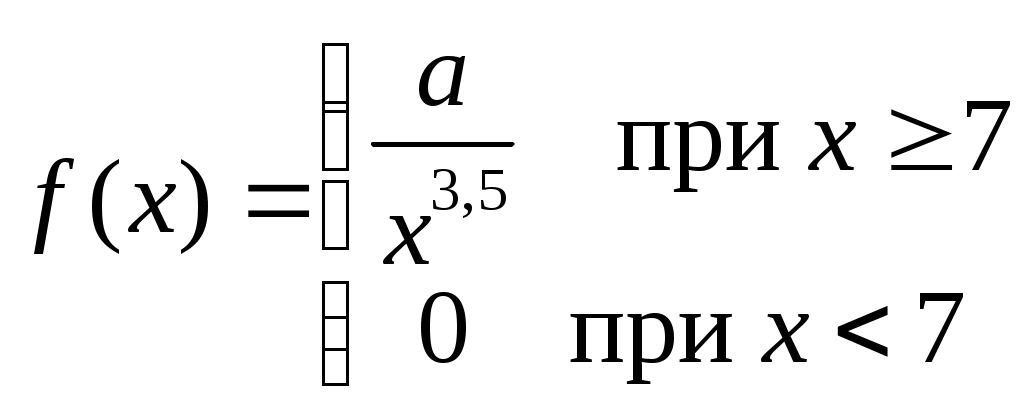 Воспользуемся условием нормировки: 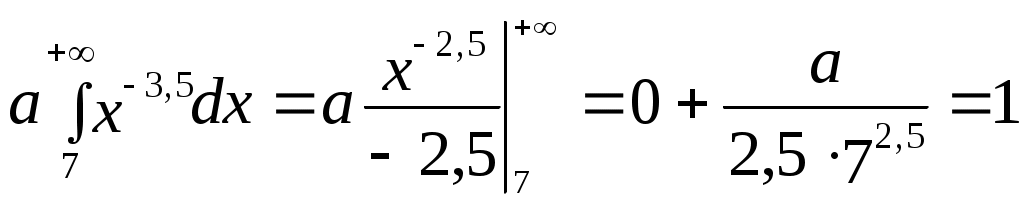 , ,следовательно, Итак, 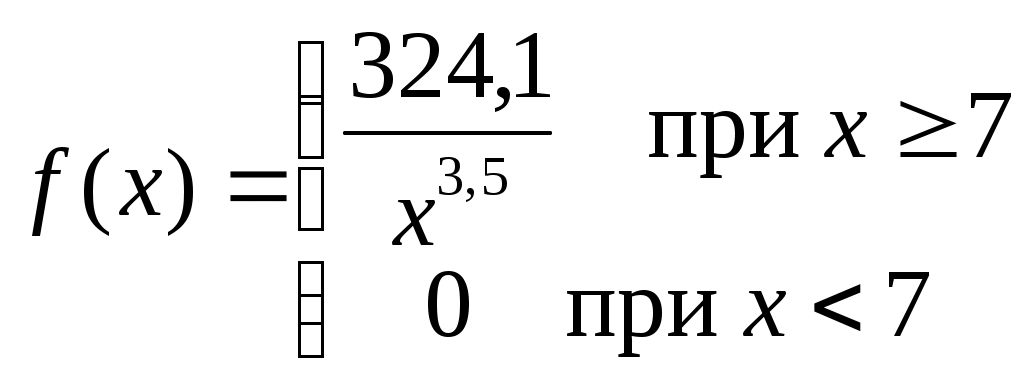 . .Функция распределения Для х<7 Для х≥7 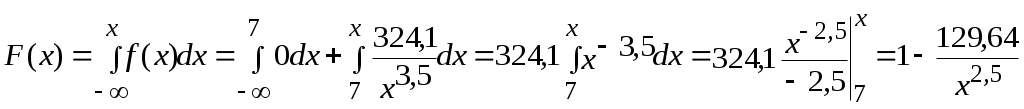 Итак, Итак,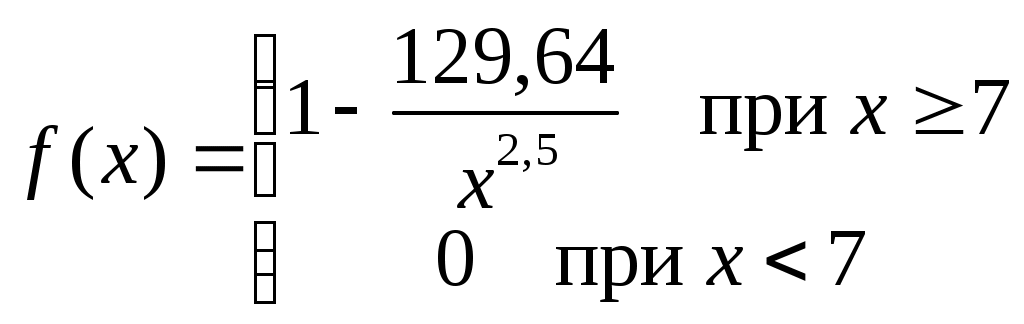 . .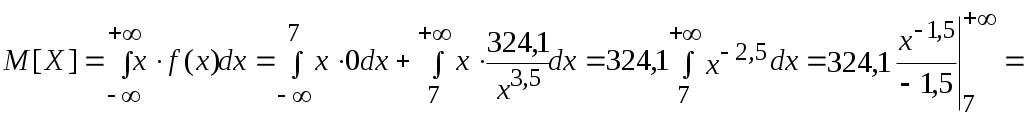 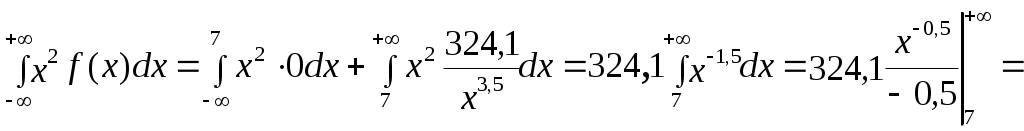 Следовательно, Т.к. по определению: следовательно, Чтобы найти х1 воспользуемся таблицами десятичных логарифмов. По таблице антилогарифмов Таким образом Пример 4.15. Найти дисперсию случайной величины Х, заданной функцией распределения 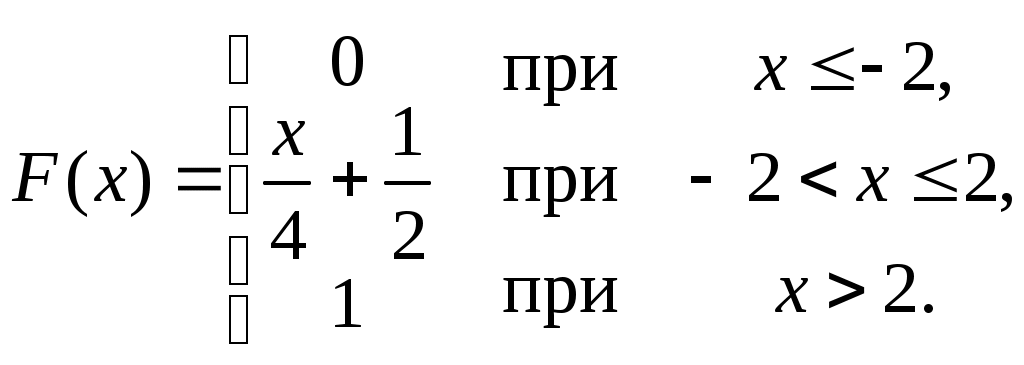 Решение. Найдем плотность распределения: 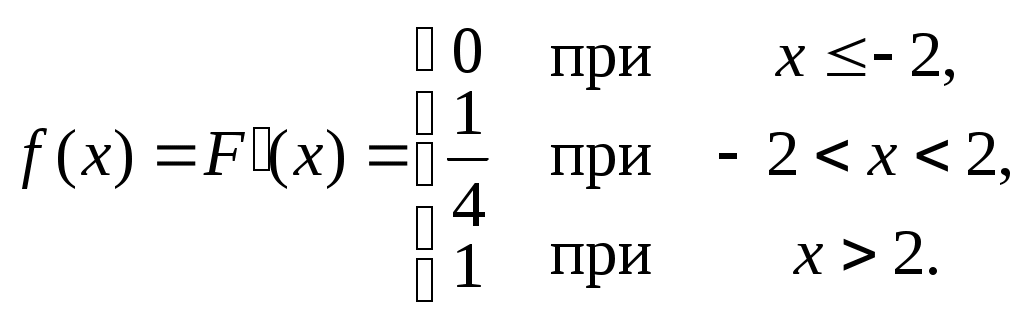 Найдем математическое ожидание (подынтегральная функция нечетная, пределы интегрирования симметричны относительно начала координат). Найдем искомую дисперсию, учитывая, что М(Х)=0: Пример 4.16. Дана плотность вероятности непрерывной случайной величины: 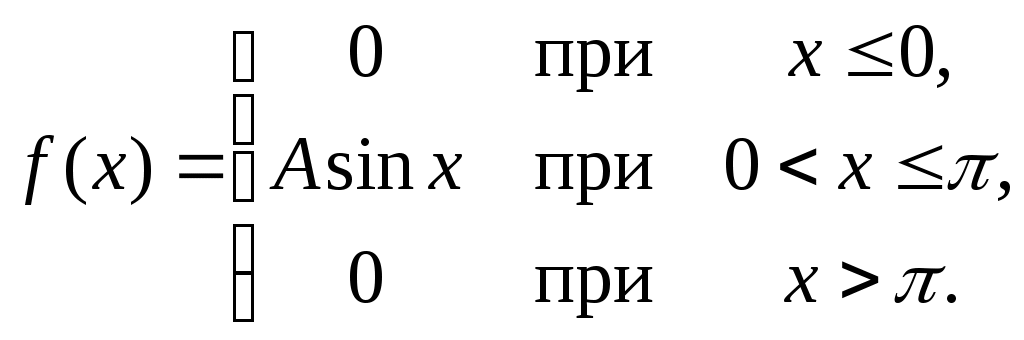 Найти интегральную функцию Решение. 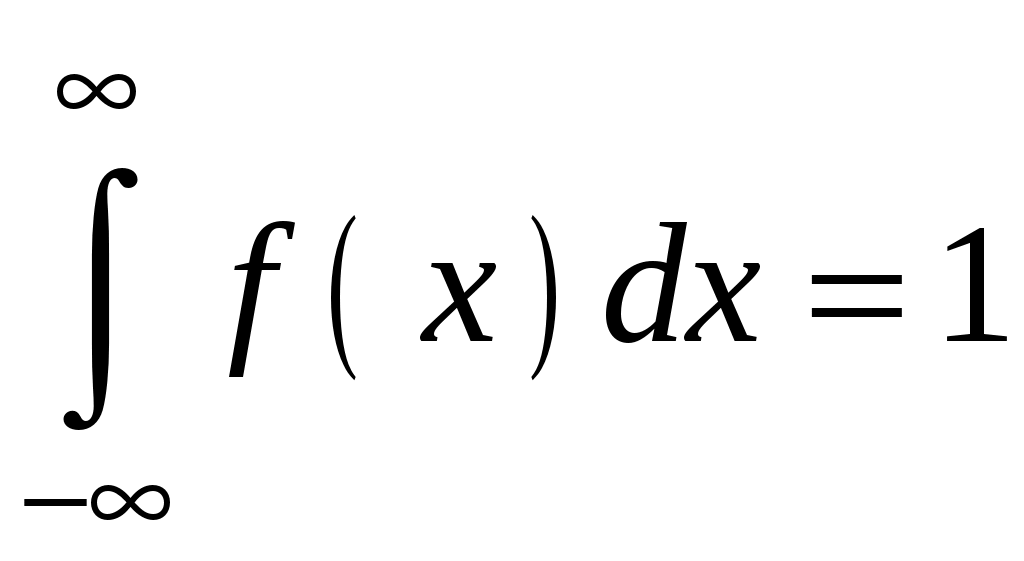 , ,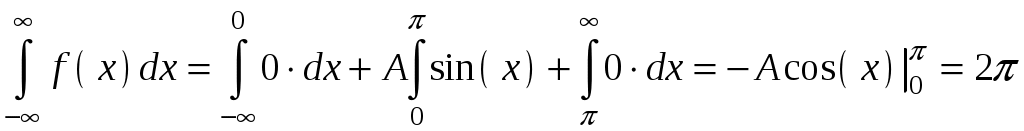 ; ;Итак: 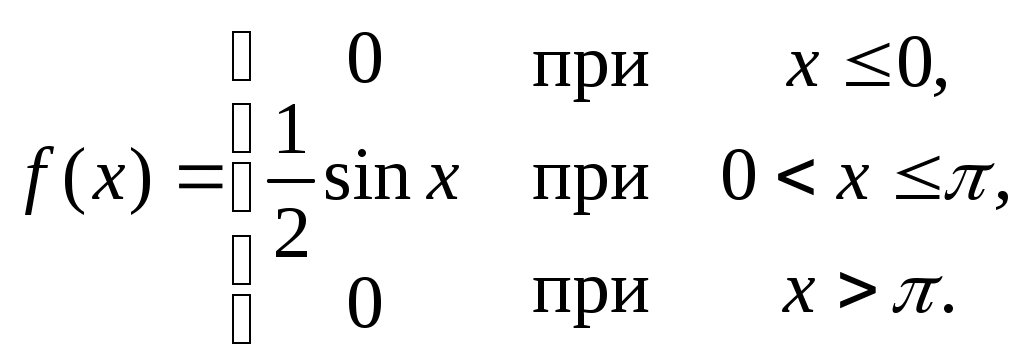 1) 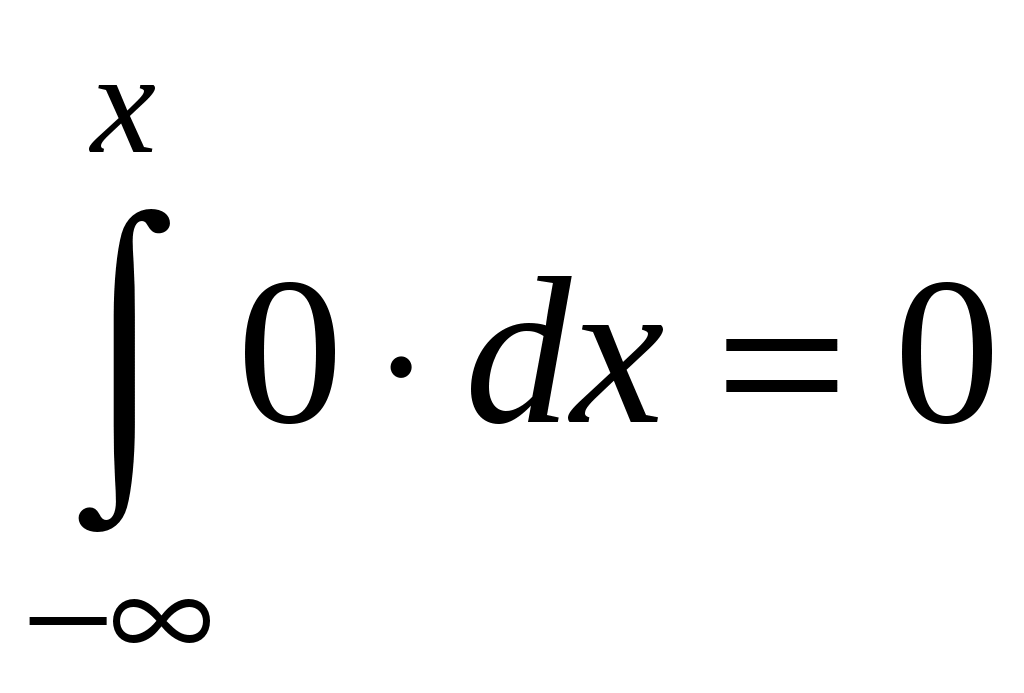 ; ;2) 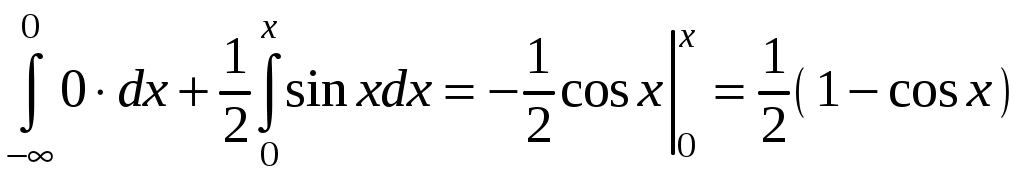 ; ;3) 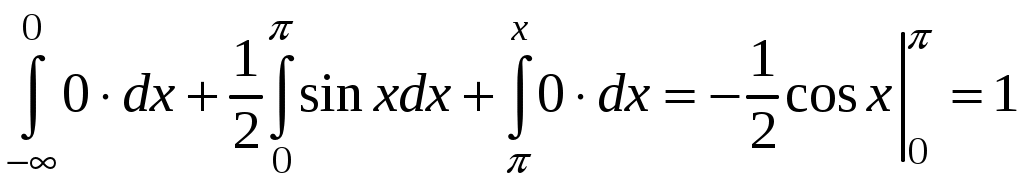 . .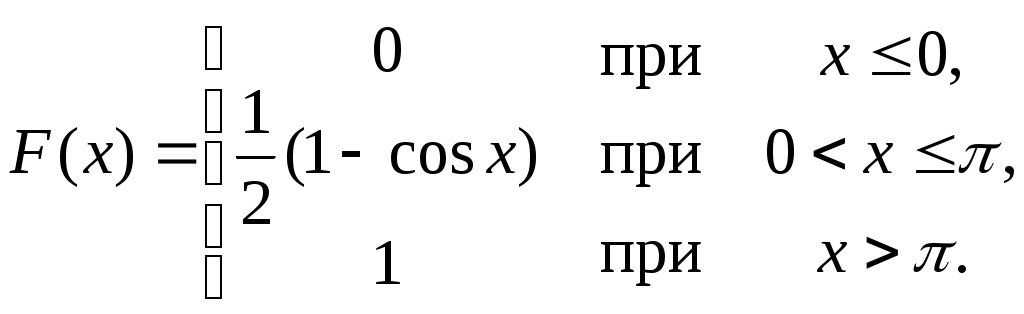 Пример 4.17. Случайная величина Х задана плотностью вероятности: 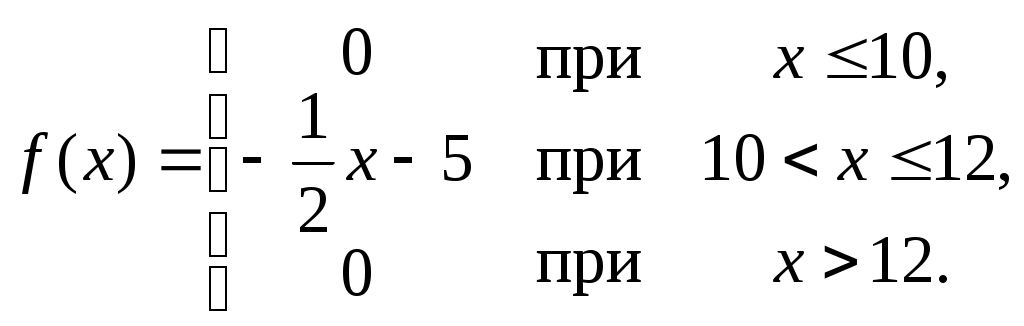 . .Найти числовые характеристики величины Х. Решение. 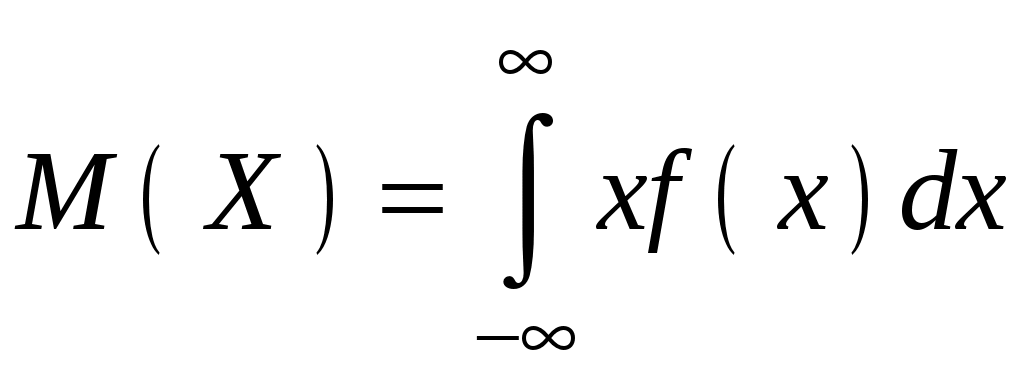 , , 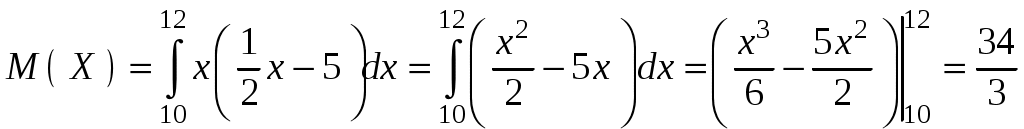 . .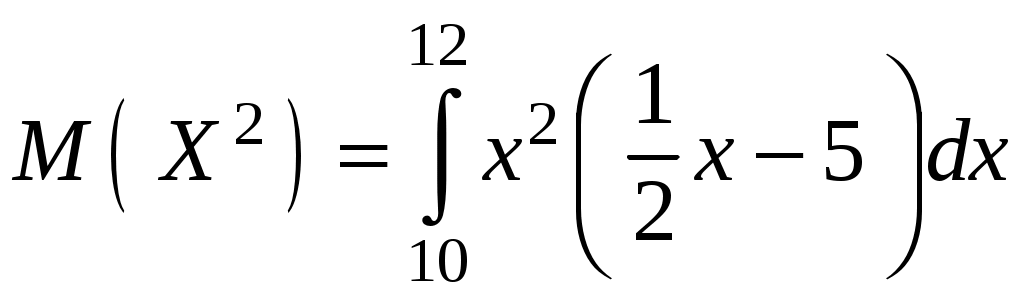 , , Пример 4.18. Автобус идет с интервалом 10 мин. Найти плотность вероятности и интегральную функцию распределения, построить их графики для времени ожидания автобуса при случайном выходе к остановке. Найти также числовые характеристики. Решение.  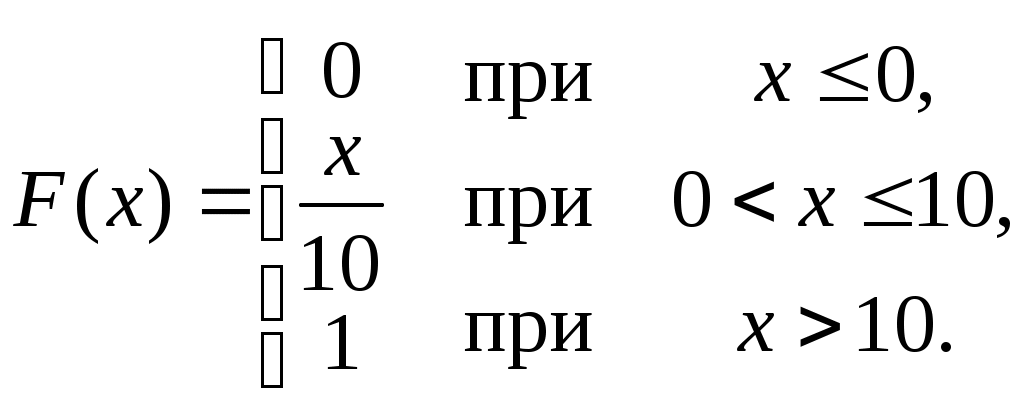 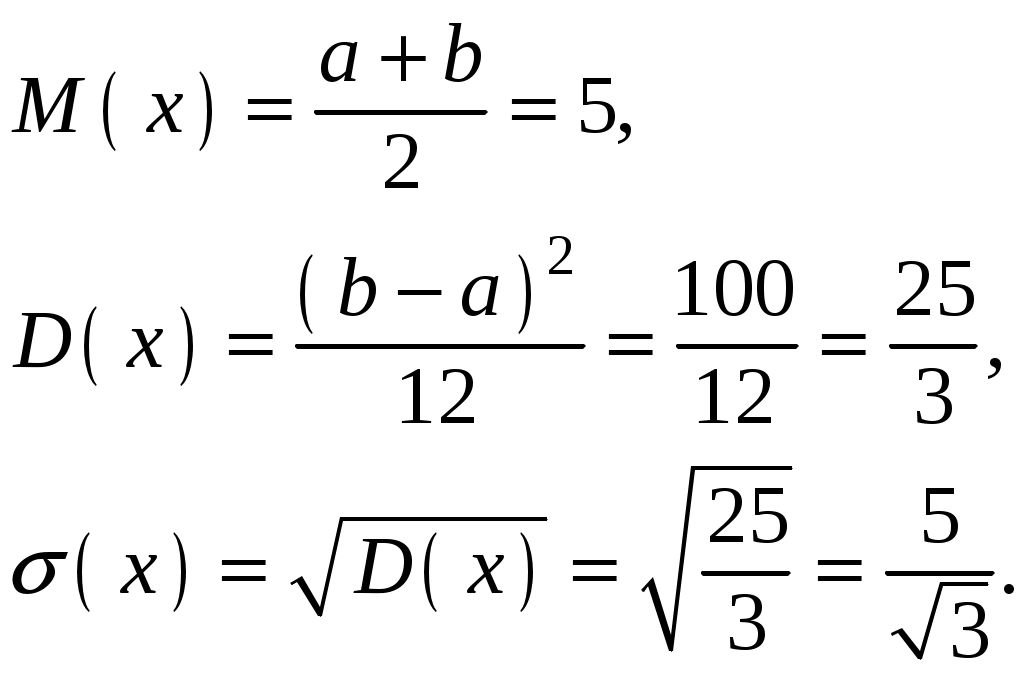 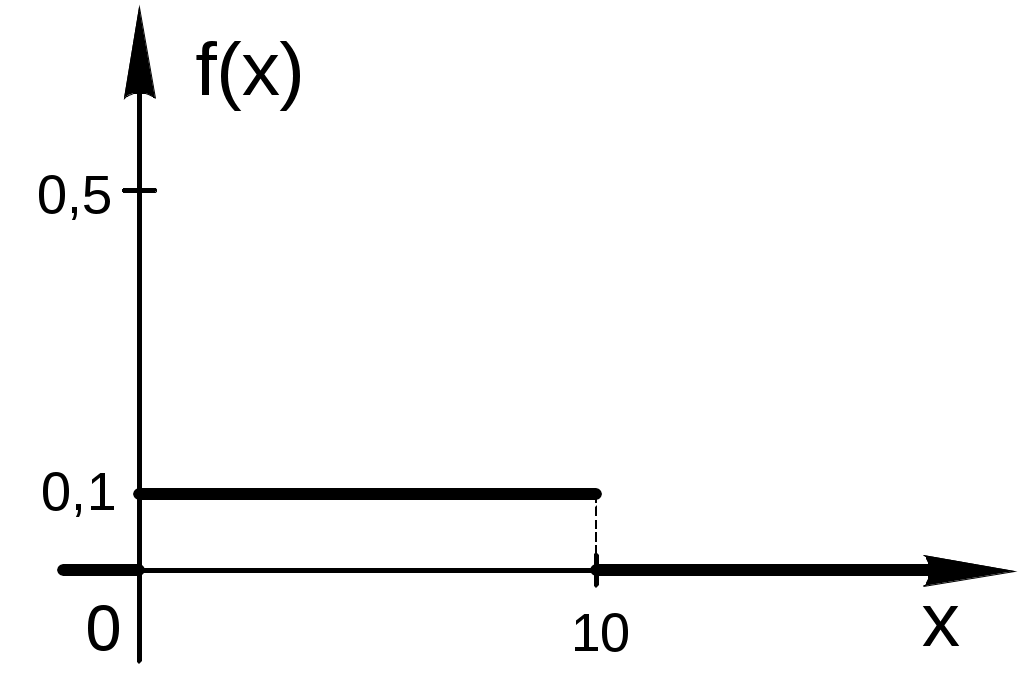 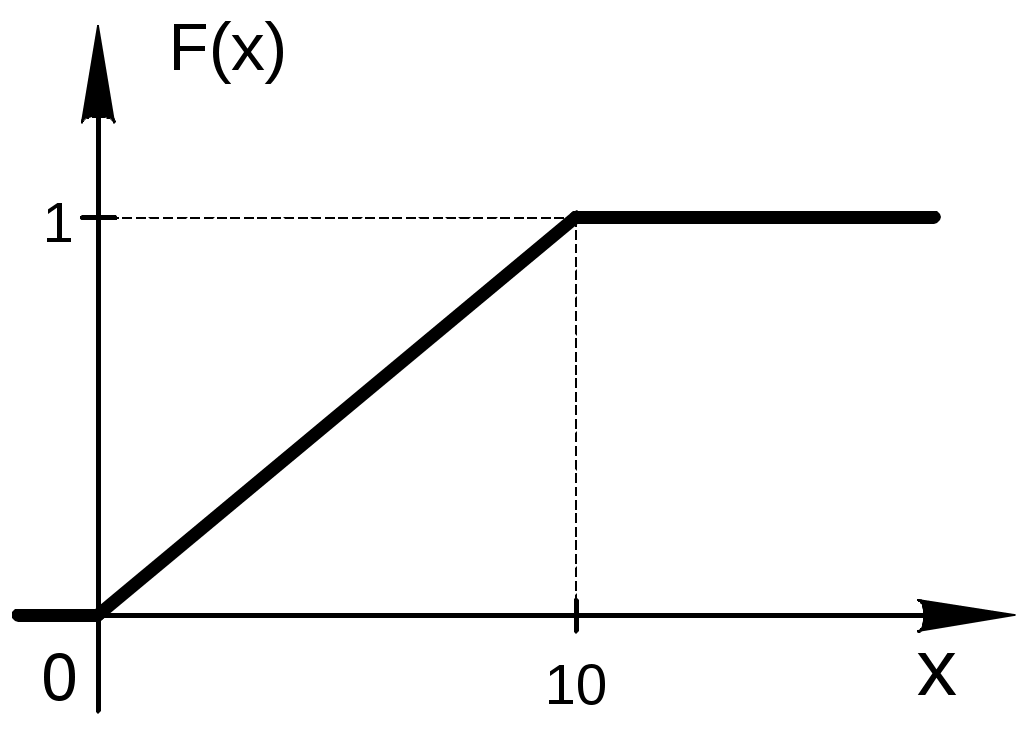 Пример 4.19. Цена деления шкалы амперметра равна 0,1А. Показания округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02А. Решение. Ошибку округления отсчета можно рассматривать как случайную величину Х, которая распределена равномерно в интервале между двумя соседними целыми делениями. Плотность равномерного распределения f(x)=1/(b-a), где (b-a) – длина интервала, в котором заключены возможные значения Х; вне этого интервала f(x)=0. В рассматриваемой задаче длина интервала, в котором заключены возможные значения Х, равна 0,1, поэтому f(х)=1/0,1=10. Легко сообразить, что ошибка отсчета превысит 0,02, если она будет заключена в интервале (0,02, 0,08). По формуле Пример 4.20. Написать плотность и функцию распределения показательного закона, если параметр λ=5. Решение. Подставив λ=5 получим: Пример 4.21. Непрерывная случайная величина Х распределена по показательному закону, заданному плотностью вероятности Найти вероятность того, что в результате испытания Х попадает в интервал (0,13, 0,7). Решение. Используем формулу Учитывая, что, по условию, a=0,13, b=0,7, λ=3, и пользуясь таблицей значений функции Пример 4.22. Найти математическое ожидание показательного распределения Решение. Используем формулу Учитывая, что f(х)=0 при х<0 и Интегрируя по частям по формуле Получим u=x, Итак, математическое ожидание показательного распределения равно обратной величине параметра λ. Пример 4.23. Найти: а) дисперсию; б) среднее квадратическое отклонение показательного распределения, заданного плотностью вероятности: Решение. а) Используем формулу Учитывая, что f(х)=0 при х<0, Интегрируя дважды по частям, найдем Следовательно, искомая дисперсия Т.е. дисперсия показательного распределения равна величине, обратной б) Найдем среднее квадратическое отклонение: Т.е. среднее квадратическое отклонение показательного распределения равно величине, обратной λ. Пример 4.24. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины соответственно равны 10 и 2. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале Решение. 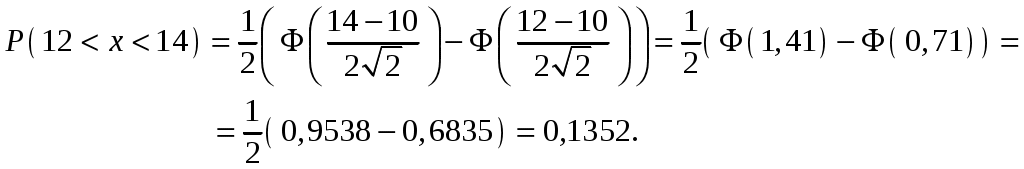 Пример 4.25. Автомат изготавливает шарики. Шарик считается годным, если отклонение Х диаметра шарика от проектного размера по абсолютной величине меньше 0,7мм. Считая, что случайная величина Х распределена нормально со средним квадратическим отклонением Решение. Так как Х – отклонение диаметра от проектного, то 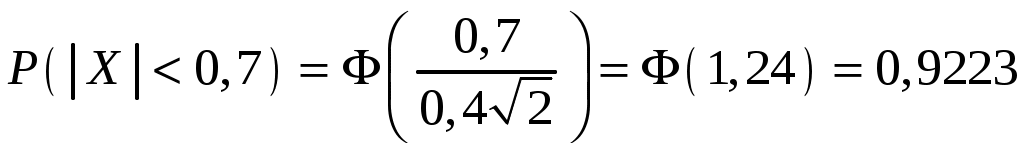 . .Таким образом, вероятность отклонения заданного размера равна 0,92. Отсюда следует, что примерно 92 шарика из 100 окажутся годными. Пример 4.26. Бомбардировщик пролетавший вдоль моста, длина которого 30м и ширина 8м, сбросил бомбы. Случайные величины Х и Y (расстояние от вертикальной и горизонтальной осей симметрии моста падения бомб), независимы и распределены нормально со средними квадратическими отклонениями, соответственно равными 6м и 4м, и математическими ожиданиям равными нулю. Найти: а) вероятность попадания в мост одной бомбы; б) вероятность разрушения моста, если сброшены две бомбы, причем известно, что для разрушения моста достаточно одного попадания. Решение. а) 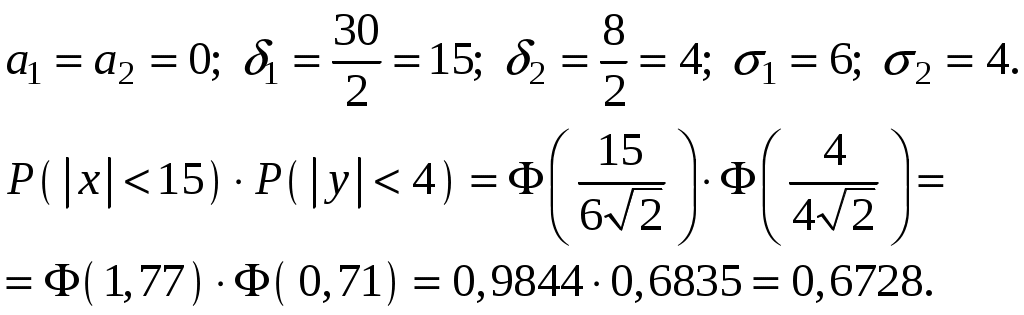 б) Задания для самостоятельного решения 4.1. Случайная величина X задана на всей оси Оx функцией распределения Найти вероятность того, что в результате испытания величина X примет значение, заключенное в интервале (0, 1). 4.2. Случайная величина X задана функцией распределения 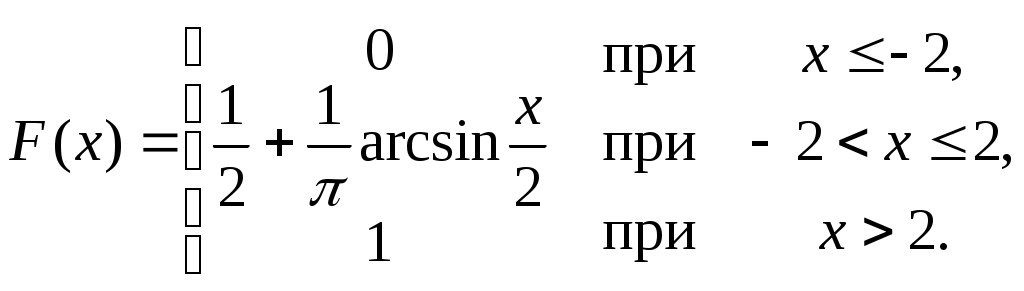 Найти вероятность того, что в результате испытания величина X примет значение, заключенное в интервале (-1; 1). 4.3. Функция распределения непрерывной случайной величины X (времени безотказной работы некоторого устройства) равна Найти вероятность безотказной работы устройства за время 4.4.Случайная величина Х задана следующим образом: 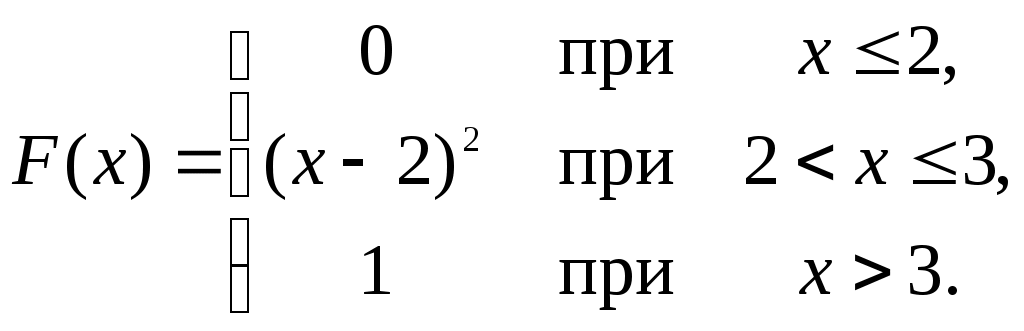 Найти Вычислить числовые характеристики и вероятность попадания случайной величины в интервал (2,5; 3,5). 4.5. Случайная величина X задана функцией распределения 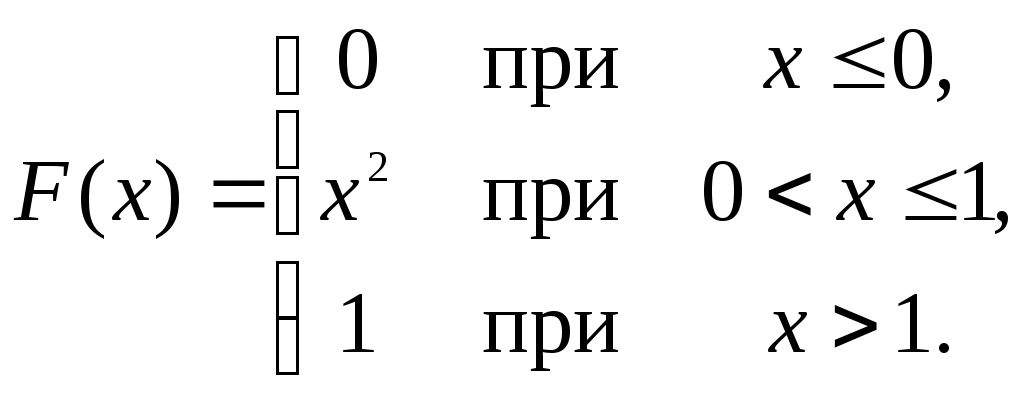 Найти вероятность того, что в результате четырех независимых испытаний величина Х равно три раза примет значение, принадлежащее интервалу (0,25; 0,75). 4.6. Дана функция распределения непрерывной случайной величины Х: 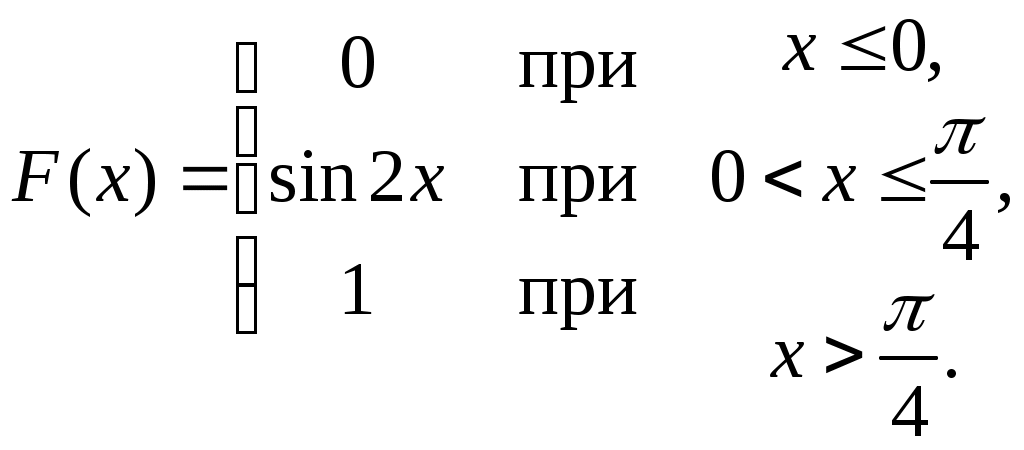 Найти плотность распределения f(х). 4.7. Непрерывная случайная величина Х в интервале (0, ∞) задана плотностью распределения Найти вероятность того, что Х примет значение, принадлежащее интервалу (1; 2). 4.8. Плотность распределения непрерывной случайной величины Х в интервале ( Найти вероятность того, что в трех независимых испытаниях Х примет ровно два раза значение, заключенное в интервале (0, 4.9. Задана плотность распределения непрерывной случайной величины Х: 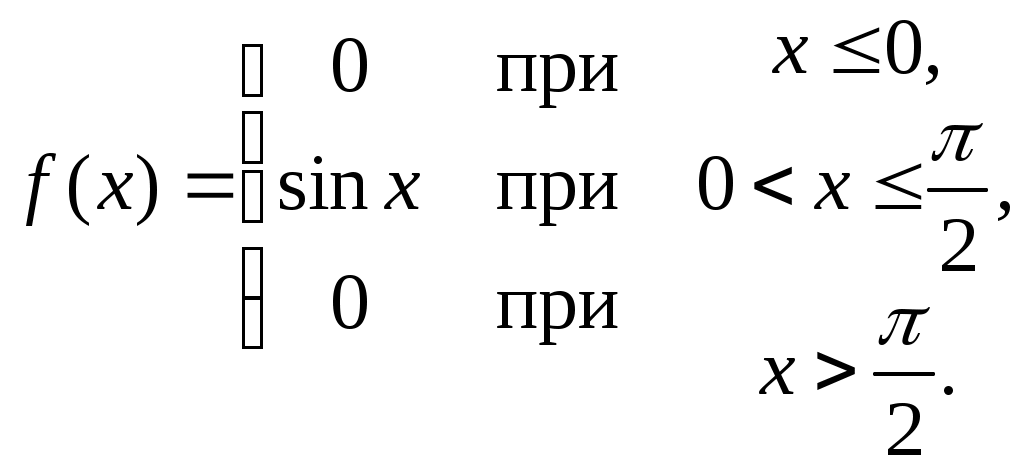 Найти функцию распределения F(х). 4.10. Задана плотность распределения непрерывной случайной величины Х: 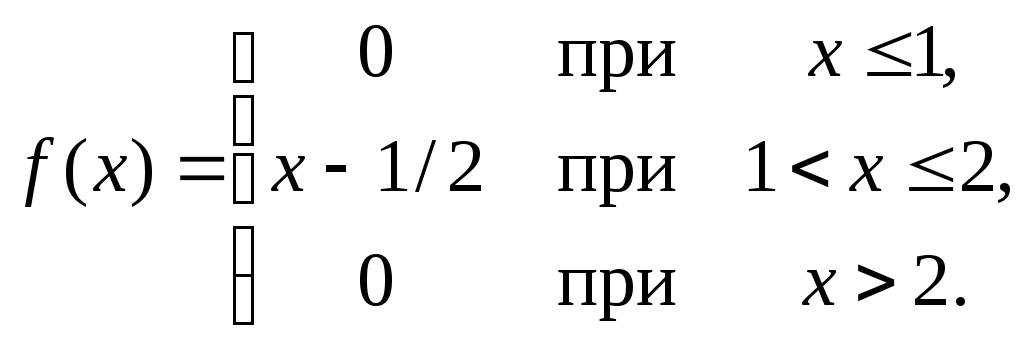 Найти функцию распределения F(х). 4.11. Задана плотность распределения непрерывной случайной величины Х: 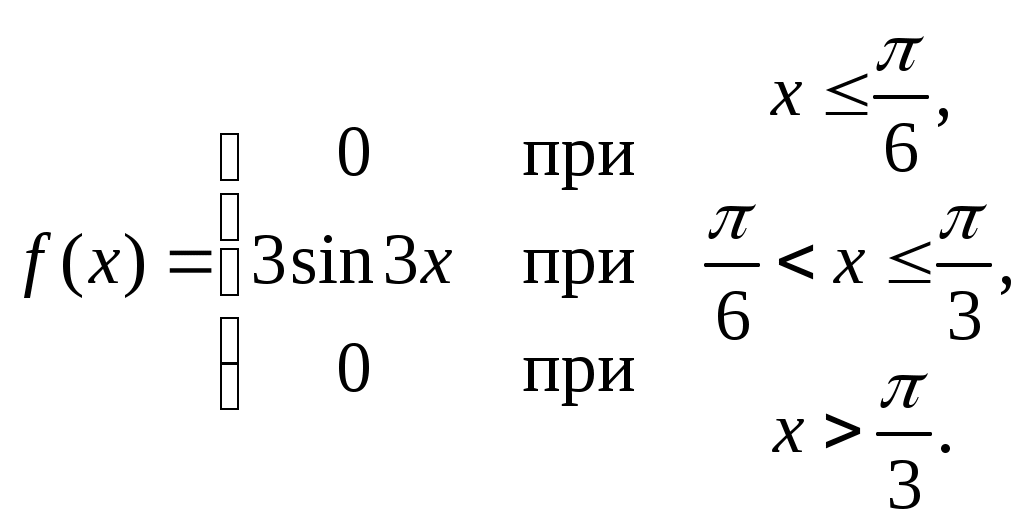 Найти функцию распределения F(х). 4.12. Плотность распределения непрерывной случайной величины Х задана на всей оси Ох равенством Найти постоянный параметр С. 4.13. Плотность распределения непрерывной случайной величины Х в интервале (0, π/2) равна f(x)=Csin2x; вне этого интервала f(х)=0. Найти постоянный параметр С. 4.14. Плотность распределения непрерывной случайной величины Х задана в интервале (0, 1) равенством f(x)=Сarctgx; вне этого интервала f(x)=0. Найти постоянный параметр С. 4.15. Случайная величина Х задана плотностью распределения f(х)=(1/2)х в интервале (0; 2); вне этого интервала f(х)=0. Найти математическое ожидание величины Х. 4.16. Случайная величина Х задана плотностью вероятности (распределение Лапласа) Найти математическое ожидание величины Х. 4.17. Случайная величина Х задана плотностью распределения Найти: а) параметр с; б) математическое ожидание величины Х. 4.18. Случайная величина Х задана плотностью распределения f(x)=cosx в интервале (0, Найти математическое ожидание функции 4.19. Случайная величина Х задана плотностью распределения f(x)=x+0,5 в интервале (0; 1); вне этого интервала f(х)=0. Найти математическое ожидание функции 4.20. Случайная величина Х распределена нормально с математическим ожиданием Чему равна вероятность попадания Х в интервал (35; 40)? 4.21. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка: а) меньшая 0,04; б) большая 0,05. 4.22. Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 5 мин. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее 3 мин. 4.23. Минутная стрелка электрических часов перемещается скачком в конце каждой минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного не более чем на 20 с. 4.24. Закон равномерного распределения задан плотностью вероятности f(x)= Найти функцию распределения F(х). 4.25. Математическое ожидание нормального распределения случайной величины Х равно а=3 и среднее квадратическое отклонение σ=2. Написать плотность вероятности Х. 4.26. Написать плотность вероятности нормального распределения случайной величины Х, зная, что М(Х)=3, D(Х)=16. 4.27. Нормально распределенная случайная величина Х задана плотностью Найти математическое ожидание и дисперсию Х. 4.28. Дана функция распределения нормированного нормального закона Найти плотность распределения f(х). БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Бабайцев, В.А. Математика в экономике. Теория вероятностей: Курс лекций /В.А. Бабайцев, А.В. Браилов, А.С. Солодовников. – М.: ФА, 2002. 2. Беляев, Ю.К. Основные понятия и задачи математической статистики / Ю.К. Беляев, В.П. Носко. – М.: Изд-во МГУ, ЧеРо, 1998. 3. Высшая математика для экономистов // под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2001. 4. Венцель, Е.С. Теория вероятностей. /Венцель, Е.С. Овчаров Л.А. – М.: Наука, 1973. 5. Гмурман, В.Е. Теория вероятностей и математическая статистика. /Гмурман В.Е. – М.: Высшая школа, 2000. 6. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике./ Гмурман В.Е. – М.: Высшая школа, 2000. 7. Карасев, А.И. Теория вероятностей и математическая статистика. Методические указания. /Карасев А.И., Кремер Н.Ш. – М., Экономическое образование, 1995. 8. Колемаев, В.А. Теория вероятностей и математическая статистика /В.А. Колемаев, В.Н. Калинина. – М.: ИНФР А-М, 1999. – 302 с. 9. Кремер, Н.Ш. Теория вероятностей и математическая статистика /Н.Ш. Кремер – М.: ЮНИТИ-ДАНА, 2000. – 543 с. 10. Математика в экономике /А.С. Солодовников, В.А Бабайцев, А.В. Браилов, И.Г. Шандра. – М.: Финансы и статистика, 2003. – Ч. 1 – 384 с.; Ч. 2 – 560 с. 11. Практикум но высшей математике для экономистов // под ред. Н.Ш. Кремера. – М.: ЮНИТИ – ДАНА, 2002. 12. Пугачев, В.С. Теория вероятностей и математическая статистика / В.С. Пугачев – М.: ФИЗМАЛИТ, 2002. – 496 с. 13. Руководство к решению задач с экономическим содержанием по курсу высшей математики // под ред. А.И. Карасева и Н.Ш. Кремера.– М.: Экономическое образование, 1989. 14. Солодовников, А.С. Математика в экономике./А.С. Солодовников, Б.А. Бабайцев, А.В. Браилов. – М.: Финансы и статистика, 1998. Ч.1. ОГЛАВЛЕНИЕ
| ||||
