Хрестоматия. Петухов. Том 3. Книга 2. Учебник по общей психологии, предназначено для проведения семинарских занятий по данному курсу и самостоятельного чтения

• Название: Учебник по общей психологии, предназначено для проведения семинарских занятий по данному курсу и самостоятельного чтения
• Анкор: Хрестоматия. Петухов. Том 3. Книга 2.doc
• Дата: 22.09.2018
• Размер: 20.88 Mb.
• Имя файла: Хрестоматия. Петухов. Том 3. Книга 2.doc
• Тип: Учебник; #24954
• страница: 26 из 53

только впечатление относительной ско­
рости движущихся объектов и ничего не говорит об абсолютной (или специфической)
скорости, которую можно было бы выразить в см/с или ж/ч. Для оценок абсолютной
скорости учет удаленности, по-видимому, является обязательным. Подобное различение
было проведено в связи с восприятием размера <...>.

² См.: Каи D. The World of Colour. Kegan Paul, Trench, Trubner & Co., 1935.

258

Тема 17. Экспериментальные исследования восприятия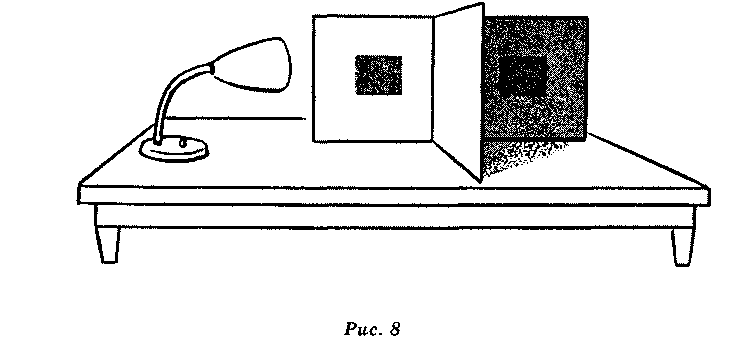

щенной с одного боку от перегородки, освещал фон по обе стороны от перегородки неоднородно. Одна сторона фона оказывается в тени перего­родки. Образец на одной стороне фона (правая сторона на рис. 8) при­нимается за стандартный. Наблюдатель должен на другой стороне фона, ближней к лампе, подобрать образец серого цвета, воспринимаемый та­ким же, как и стандартный. (Для этого эксперимента необходимы стан­дартные образцы всех оттенков серого. Для каждого образца определя­ется коэффициент отражения.)

Другой способ проведения эксперимента основан на использовании цветового круга. Белый и черный картонные диски вдеваются друг в друга так, как показано на рис. 9. Когда такая пара дисков приводится с помощью электродвигателя во вращение, наблюдатель видит серый цвет, его интенсивность зависит от количественного отношения белого и черного. Один из таких дисков с заданным серым цветом выбирается в качестве стандартного, а другой, в котором соотношение белого и чер-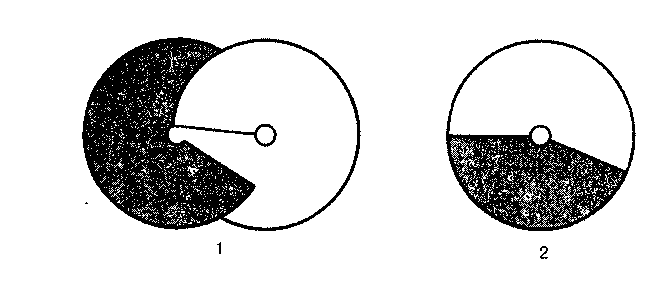



Рис. 9

Рок И. [Константность восприятия]

259

ного секторов может меняться, используется в качестве сравниваемого. Цветовые круги позволяют устранить восприятие неровностей или тек­стуры поверхности, так называемую микроструктуру.

Если расположение на рис. 8 оказалось бы таким, что оба образца отражали одинаковый по абсолютной интенсивности свет, то с левой сто­роны, чтобы компенсировать большее количество света, падающего от лампы, подбирался бы образец с небольшим коэффициентом отражения. С другой стороны, если бы имелась полная константность цвета, наблю­датель выбирал бы серый, коэффициент отражения которого равен стан­дартному. Обычно наблюдатели выбирают образец, серый цвет которого несколько темнее стандартного, но не намного. Таким образом, как пра­вило, в экспериментах данного типа проявляется сильная тенденция к константности. Подобный результат — хорошая иллюстрация того, что обычно происходит в реальной жизни.

Рис. 10

Отличие обычного подравнивания от подравнивания, которое было бы основано на равенстве ретинальных изображений двух образцов, ста­новится вполне очевидным, когда образцы рассматриваются через не­большие отверстия так, что видны только они, а не окружающий фон. Такое устройство, известное как редуцирующий экран, изображено на рис. 10. Образец, обычно подбираемый как равный стандартному, при таких условиях наблюдения разительно отличается по цвету от стан­дартного и в данном примере близок к черному. Если вслед за тем, как подравнивание произведено, поднять вдруг экран, то наблюдатель пора-

260

Тема 17. Экспериментальные исследования восприятия

жается тому, что он мог оценивать эти два образца как равные. Здесь мы, по-видимому, имеем пример восприятия, определяемого физическим равенством ретинальных изображений образцов. Результаты, получен­ные при редуцирующем экране, могут рассматриваться как подравнива­ния интенсивностей отраженного света и могут служить полезным ме­тодом измерения яркости при отсутствии необходимого прибора. Такое предположение можно подкрепить следующими доводами. Допустим, наблюдатель производит подравнивание на основе физической интенсив­ности двух ретинальных изображений. Тогда он должен компенсировать разницу в освещении разницей в коэффициентах отражения. Если, на­пример, он выбирает величину коэффициента отражения близкого к лампе участка такую, что он оказывается в три раза темнее, чем нахо­дящийся в тени стандартный образец, то это могло бы означать, что стандартный образец получает в три раза меньше света.

Тенденцию к константности для наблюдателя или группы наблюда­телей можно выразить и количественно (см. рис. 11). Если наблюдатель подравнивает образцы на основе абсолютной интенсивности, выбирая ко­эффициент отражения сравниваемого объекта, так, чтобы компенсировать разницу в освещении, то никакой тенденции к константности он не прояв­ляет; если же он подравнивает образцы, выбирая коэффициент отражения равным стандарту, он проявляет полную константность. И если при под­равнивании он выбирает, как обычно и бывает, промежуточный между

Рок И. [Константность восприятия]

261

этими крайними случаями коэффициент отражения, то степень констант­ности может выражаться значением коэффициента отражения по отноше­нию к 0 и 100% константности.

Например, предположим, что стандарт (правая часть рис. 8) имеет ко­эффициент отражения 30 и на него попадает только треть от освещения, которое падает на сравниваемый образец. Тогда точка, соответствующая 0% константности, на рис. 11 означала бы подравнивание на ¹/₃— от 30 или 10 единиц (компенсируется различие в освещенности). Точка, соот­ветствующая полной константности, означала бы подравнивание к 30 единицам. Следовательно, интервал между нулевой константностью и полной константностью будет равен 30 минус 10 или 20. Если испытуе­мый выбирает при подравнивании к стандарту коэффициент отражения, равный 25, то интервал между этим подравниванием и отсутствием константности будет 25 минус 10 или 15. Отношение этого интервала к полному интервалу будет отношением 15 к 20, или 75%. Этот метод опи­сания степени константности был введен Эгоном Брунсвиком¹. Его мож­но применить и к другим перцептивным константностям, трактуя одну точку как подравнивание к проксимальному стимулу, вторую точку — как подравнивание при полной константности, а третью точку — как по­лученное подравнивание.

¹ См.: Brunswik E. Zur Entwicklung der Albedowahrnehmung // Zeitschrift fur Psycho-logie. 1929. 109. S. 40-115. Модифицированное отношение с использованием логарифми­рования было введено затем Таулесом (см.: Thouless R. Phenomenal regression to the real object. I. // British Journal of Psychology. 1931. 21. P. 339-359). Мера константности во многом зависит от различий в условиях наблюдения. В данном примере если стандарт­ный образец вместо 1/₃ получает только 1/₁₀ от света, падающего на сравниваемый обра­зец, то, даже если испытуемый еще больше отклонился бы от константности, подравни­вая стандарт к коэффициенту отражения 24, отношение Брунсвика оказалось бы выше 75%. Этим можно объяснить тот парадоксальный факт, что во многих экспериментах по константности величины, формы, по ахроматической цветовой константности с увеличе­нием разницы в расстоянии, ориентации или освещенности между стандартным и сравнива­емым предметами растет тенденция к константности. Обычно подравнивания все более и более отклоняются от константности, поскольку зависят от таких различий в условиях наблюдения, но отклоняются гораздо медленнее, чем это было бы при подравнивании проксимального стимула. Поэтому величина константности часто возрастает.

Р. Вудвортс

ОТНОШЕНИЕ МЕЖДУ ВЕЛИЧИНОЙ

И РАССТОЯНИЕМ¹

Константность величины

Этот термин употребляется в двух различных смыслах. Предмет, размер которого известен, например, человек или автомобиль, всегда оценивается как одинаковый по величине, даже если размер еетчаточ-ного образа этого предмета меняется во много раз. В терминах нашей формулы А сохраняет постоянное значение, так как изменения а ком­пенсируются за счет оценки D: по мере уменьшения сетчаточного обра­за человек или автомобиль кажутся более удаленными. В этом смысле константность величины есть признак удаленности. Иногда при очень больших расстояниях или в необычных условиях, например, при наблю­дении за предметами с высокой башни, константность нарушается, но даже в этих случаях суждение о размере объекта часто оказывается пра­вильным².

Вторая ситуация, обнаруживающая константность величины, отно­сится к случаям, где оценка размера неизвестного объекта осуществля­ется на основе а и D. Эти случаи в ряде отношений более просты, поэто­му сначала рассмотрим их.

¹ Хрестоматия по ощущению и восприятию / Под ред. Ю.В.Гиппенрейтер, М.Б.Ми-
халевской. М.: Изд-во Моск. ун-та, 1975. С. 320-324.

² См.: Gibson J.J. The perception of the visual world. Bost.: Houghton Mifflin, 1950.

Вудвортс Р. Отношение между величиной и расстоянием

263

Оценка величины как функция признаков удаленности

Хотя эта проблема исследовалась многими другими авторами, мы предпочитаем начать с описания экспериментов Холуэя и Боринга¹.

В этих экспериментах наблюдатель помещался в месте пересечения двух длинных коридоров, расходящихся под углом 90°. В одном коридо­ре на расстоянии 3 ж от испытуемого находился «сравниваемый стимул». Он представлял собой световое пятно, размер которого испытуемый мог менять. В другом коридоре на различных расстояниях от наблюдателя (от 3 до 36 м) предъявлялось аналогичное пятно. Это был стандартный сти­мул, фактические (линейные) размеры которого менялись вместе с рас­стоянием так, что он всегда имел один и тот же угловой размер, равный 1°. Испытуемому ставилась задача так подобрать размер «сравниваемого стимула», чтобы он казался равным «стандартному стимулу».

Результаты приведены на рис. 1. Прежде чем перейти к их обсуж­дению, разберемся в обозначениях на графике. Рассмотрим пунктирную линию, идущую параллельно оси абсцисс. Эта прямая представляет мно­жество значений «сравниваемого стимула», которые подобрал бы наблю­датель, если бы он руководствовался угловым размером «стандартного стимула» (необходимо помнить, что «стандартный стимул» всегда состав­лял 1° независимо от удаленности). Теперь рассмотрим пунктирную ли­нию, которая располагается по диагонали графика. Она описывает мно­жество значений, которые мы получили бы в случае «полной констант­ности», т.е. если бы наблюдатель всегда точно подравнивал величину «сравниваемого стимула» к действительной величине «стандартного сти­мула». Тригонометрически можно показать, что на расстоянии 12 j от наблюдателя 1° занимает объект с линейным размером 21 см, а на рас­стоянии 24 м — объект с линейным размером 42 см и т.д., как это и показано на графике.

Обратимся теперь к результатам. Когда испытуемому были обес­печены условия нормального бинокулярного зрения, он давал результаты, представленные прямой 1. Наблюдался даже незначительный эффект сверхконстантности, что возможно было связано со сверхкомпенсацией или некоторой переоценкой удаленности - ведь наблюдатель смотрел вдоль длинного коридора. Прямая 2 показывает результаты, полученные в усло­виях монокулярного зрения. Восприятие удаленности все еще хорошее: об этом говорит тот факт, что полученные значения находятся в соответствии с законом константности. Но как только был введен искусственный зра­чок, устранивший дополнительные признаки удаленности, оценки наблю­дателя оказались в промежуточном положении между оценками, соответ-

¹ См.: Holway A.H., Boring E.G. Determinants of apparent visual size with distance variant // Amer. J. Ps. 1941. 64. P. 21-37.

264

Тема 17. Экспериментальные исследования восприятия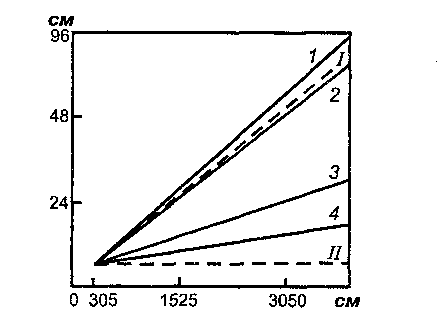

Рис. 1. Воспринимаемая величина как функция признаков удаленности. «Стан­дартным стимулом» является световое пятно, помещаемое на разных расстоя­ниях от наблюдателя. Физические размеры этого пятна возрастают пропорцио­нально увеличению расстояния, так что угловые размеры сетчаточного образа остаются неизменными. Наблюдатель варьирует размеры «сравниваемого стиму­ла» до тех пор, пока не начинает воспринимать его равным «стандартному». Удаленность «сравниваемого стимула» постоянна и равна 3 м. Высокая констан­тность величины имеет место при условиях 1 и 2 (бинокулярное и монокулярное зрение соответственно). В условии 3 признаки удаленности частично исключают­ся введением искусственного зрачка, что приводит к уменьшению константнос­ти. Дальнейшее исключение признаков с помощью штор, снимающих подсветы (условие 4), заставляет наблюдателя подбирать размеры «сравниваемого стимула» почти в полном соответствии с угловой величиной «стандарта»: ось абсцисс — расстояние до стандартного стимула {см); ось ординат — видимый размер пятна (см); I— константность величины; II- постоянный угловой размер¹

ствующими закону константности и закону угла зрения (линия 3). При этом еще сохранились остатки признаков глубины в виде слабых подсве­тов от дверей, расположенных вдоль коридора. Когда же и они были ис­ключены с помощью черных штор, результаты еще больше приблизились к закону угла зрения (прямая 4). Позднее Личтон и Лурье² еще более ог­раничили признаки удаленности, используя экраны, которые не позволя­ли наблюдателю видеть ничего, кроме светового пятна. В этих условиях не оставалось даже и намека на константность величины. Эти два экспери­мента ясно показывают, что наблюдатель может правильно оценивать раз­меры неизвестного ему предмета лишь в той мере, в какой у него есть на­дежные источники информации об его удаленности.

¹ См.: Holway A.H., Boring E.G. Determinants of apparent visual size with distance
variant // Amer. J. Ps. 1941. P. 21-37.

² См.: Liehten W., Lurie S. A new technique for the study of perceived size // Amer. J.
Ps. 1950. 63. P. 281-282.

Вудвортс Р. Отношение между величиной и расстоянием 265

Обсуждение результатов

Результаты, полученные в ситуациях 1 и 2, соответствуют ожида­емым; при данном а и адекватной оценке Dнаблюдатель находит из уравнения о = A/Dнеизвестное А. Но что происходит в ситуации 4, ког­да Dстановится также неизвестным? Полученные здесь результаты мож­но объяснить двояко. Во-первых, можно предположить, что наблюдатель принимает решение исключительно на основе оценки зрительного угла (а) или проксимального стимула¹. Это предположение соответствует результатам, но может быть ошибочным в отношении механизмов. Еще неизвестно, может ли человек оценивать размеры своего сетчаточного образа или величину соответствующего ему угла. Кроме того, мы никог­да не воспринимаем объекты как находящиеся на неопределенных рас­стояниях. Это наводит нас на второе объяснение результатов ситуации 4. Если не существует адекватных признаков ни величины объекта, ни удаленности его, мы автоматически принимаем некоторые совместимые значения обеих переменных. Например, при световом пятне диаметром 12,5 см на расстоянии 18 м наблюдатель может «видеть» одну из сле­дующих ситуаций: 12,5 см на расстоянии 18 м; 6,25 см на расстоянии 9 м; 25 см на расстоянии 36 м и т.д. Тот вариант, который он в действи­тельности видит, не предопределен реальной стимульной ситуацией и потому является чрезвычайно неустойчивым. При такой неопределенно­сти на восприятие могут оказывать влияние факторы, совершенно неуло­вимые. Вполне возможно, например, что в нашем случае объекты будут «видеться» на расстоянии, соответствующем конвергенции глаз наблю­дателя. Во всяком случае, мы будем иметь разумное объяснение резуль­татов, полученных в ситуации 4 (при отсутствии признаков удаленнос­ти), если предположим, что наблюдатель всегда воспринимает объект на каком-то определенном расстоянии, и вставим это воспринимаемое зна­чение Dв нашу формулу: a=A/D.

¹ См.: Koffka К. Principles of Gestalt psychology. N. Y.: Harcourt, Brace, 1935.

А.Д. Логвиненко

ПЕРЦЕПТИВНЫЕ ВЗАИМОДЕЙСТВИЯ И ПОСТРОЕНИЕ ВИДИМОГО МИРА¹

Константность видимой величины и видимой формы

Суть проблемы константности видимой величины, как и прочих кон-стантностей в зрительном восприятии, состоит в том, что видимая величи­на определяется скорее дистальным стимулом (физической величиной объекта), нежели проксимальным стимулом (величиной его сетчаточного изображения или, что то же самое, его угловой величиной). Проблема здесь в том, что, с одной стороны, если все параметры стимуляции, кроме угло­вой величины объекта, сохраняются неизменными, видимая величина стро­го следует угловой величине, т.е. имеет место психофизическая зависимость «видимая величина — угловая величина», и эта зависимость линейная. Причем достаточно увеличить угловую величину объекта на 1%, чтобы было заметно изменение его видимой величины, т.е. зрительная система весьма тонко реагирует на различия сетчаточных изображений объектов. С другой стороны, при удалении объекта мы не замечаем уменьшения его видимой величины², хотя его угловая величина уменьшается обратно пропорциональ­но удаленности. В этом легко убедиться, поместив левую ладонь на расстоя­нии 25 см от глаз, а правую — на расстоянии 50 см. Несмотря на то, что угловая величина правой ладони при этом приблизительно вдвое меньше, чем левой, обе ладони воспринимаются равными по величине.

Может сложиться впечатление, что явление константности состоит в неизменности (константности) видимой величины предметов при уменьше­нии их сетчаточного изображения, вызванного удалением этих предметов от наблюдателя. Само собой напрашивается при этом предположение о

¹ Логвиненко АД. Зрительное восприятие пространства. М.: Изд-во Моск. ун-та, 1981.
С. 178-183, 187-195.

² Если удаление не превышает нескольких метров.

Логвиненко А.Д. Перцептивные взаимодействия...

267

том, что зрительная система учитывает изменение абсолютной удаленнос­ти объекта и компенсирует уменьшение его сетчаточного изображения с удалением объекта от наблюдателя. На первый взгляд, такая точка зрения не лишена смысла, поскольку опыты показывают, что уменьшение числа признаков абсолютной удаленности (так называемая редукция признаков) приводит к исчезновению константности величины. При этом чем больше редуцированы признаки, тем менее компенсируется уменьшение сетчаточ­ного изображения объектов с увеличением удаленности¹. При полной ре­дукции наблюдается полная аконстантность видимой величины, а именно видимая величина строго следует угловой величине объекта (как иногда говорят, следует закону для угла зрения).

Брунсвик² и Таулесс³ независимо друг от друга предложили меру компенсации изменения проксимального стимула с изменением удаленно­сти (или наклона, если речь идет о форме). Они вычисляли отношение ве­личины осуществившейся компенсации к величине требуемой (для полной константности) компенсации. Это отношение получило название коэффи­циента константности. Если компенсация полная, что соответствует явлению константности, коэффициент константности равен единице. Если компенсация вовсе отсутствует, что соответствует явлению аконетантнос-ти, то коэффициент константности равен нулю. В терминах коэффициента константности результаты Холуэя и Боринга могут быть сформулированы так: редукция признаков вызывает редукцию коэффициента константнос­ти от единицы до нуля. Последующие исследования подтвердили этот факт. Переход от стимульной ситуации, богатой зрительными признаками, к ситуации, менее насыщенной ими, вызывает уменьшение коэффициента константности как для видимой величины⁴, так и для видимой формы⁵.

¹ См.: Holway AM., Boring E.G. Determinants of apparent visual size with distance
variant // Am. J. Psychol. 1941. Vol. 54. P. 21-37.

² См.: Brunswik E. Perception and the Representative Design of Psychological
Experiments. Berkeley: Los Angeles University of California Press, 1956.

³См.: Thouless R.H. Phenomenal regression to the real object. Part I // Brit. J. Psychol.
1931. Vol. 21. P. 339-359.

⁴См.: Leibowitz H.W., Harvey L.O. Size matching as function of instruction in a
naturalistic environment. // J. Exp. Psychol. 1967. Vol. 74. P. 378-382; Leibowitz H.W..
Harvey L.O. Effect of instructions,, environment, and type of test object of matched size //
J. Exp. Psychol. 1969. Vol. 81. P. 36-43.

⁵См.: Eissler K. Die Gestaltkonstanz des Sehdinge // Arch. Ges. Psychol. 1933. Vol. 88. P. 487-550; Stavrianos K.B. The relation of shape perception to explicit judgments of inclination // Arch. Psychol. 1945. 296; Langdon J. Perception of a changing shape // Quart J. Exp. Psychol. 1951. Vol. 3. P. 157-165; Langdon J. Further study in perception of changing shape // Quart. J. Exp. Psychol. 1953. Vol. 5. P. 89-107; Langdon J. The perception of three-dimensional solids // Quart. J. Exp. Psychol. 1955. Vol. 7. P. 133-146; Nelson TM., Bartley S.H. The perception of form in unstructured field // J. Gen. Psychol. 1956. Vol. 54. P. 57-63; Leibowitz H., Bussey Т., McGuire P. Shape and size constancy in photographic reproduction // J. Opt. Soc. Am. 1957. Vol. 47. P. 658-661; Epstein W.. Park J. Shape constancy: functional relationships and theoretical formulations // Psychol. Bull. 1963. Vol. 60. P. 265-288.

268

Тема 17. Экспериментальные исследования восприятия

Боринг предложил называть величину сетчаточного изображения объекта ядерным стимулом, а все остальные проксимальные стимулы, которые поставляют информацию об абсолютной удаленности и позволя­ют скомпенсировать уменьшение сетчаточного стимула, — контекстны­ми стимулами¹. Видимая величина, по его мнению, определяется балан­сом между ядерным и контекстными стимулами — чем меньше контек­стных стимулов, тем более доминирует ядерный стимул. Этот вариант объяснения константности, исходя из идеи компенсации, получил назва­ние ядерно-контекстной теории².

Серьезным недостатком любой теории константности, исходящей из идеи компенсации перспективных искажений сетчаточных изображений, является то, что это — теория для явления полной константности. Эта теория предполагает, что в ситуации, богатой признаками удаленности, происходит полная компенсация перспективных искажений сетчаточно­го образа, результатом чего является константность в зрительном воспри­ятии. Однако легко убедиться, что весьма существенное отклонение от константности видимой величины может иметь место и без редукции признаков. Для этого достаточно взглянуть вниз из окна высотного дома или из иллюминатора самолета. Люди внизу выглядят очень маленьки­ми, их видимая величина существенно меньше величины людей, нахо­дящихся рядом.

Еще более важным, на наш взгляд, представляется то обстоятель­ство, что при экспериментальном исследовании константности оказалось, что полная константность (коэффициент константности, равный едини­це) встречается крайне редко. Как правило, измеренный в эксперименте коэффициент констант-ности принимает промежуточное значение в ин­тервале между нулем и единицей. Причем, если выборка испытуемых достаточно велика, то для коэффициента константности можно получить практически любое значение. Большой интериндивидуальный разброс результатов встретился уже в первом исследовании константности види­мой формы³. Большая индивидуальная изменчивость коэффициента кон­стантности видимой формы отмечалась позднее еще рядом авторов⁴.

¹ См.: Boring E.G. The perception of objects // Am. J. Phys. 1946. Vol. 14. P. 99-107.

² См.: Allport F.H. Theories of perception and the concept of structure. N. Y.: John
Wiley and Sons, 1955.

³ См.: Thouless R.H. Individual differences in phenomenal regression // Brit. J. Psychol.
1932. Vol. 22. P. 216-241.

⁴ См.: Sheehan MM. A study of individual differences in phenomenal constancy // Arch.
Psychol. 1938. 222; Moore W. E. Experiments on the constancy of shape // Brit. J. Psychol.
1938. Vol. 29. P. 104-116; Lichte W.H. Shape constancy: Dependence upon angle of rotation.
Individual differences. // J. Exp. Psychol. 1952. Vol. 43. P. 49-57; Langdon J. Further
study in perception of changing shape // Quart. J. Exp. Psychol. 1953. Vol. 5. P. 89-107;
Langdon J. The perception of three-dimensional solids // Quart. J. Exp. Psychol. 1955.
Vol. 7. P. 133-146.

Логвиненко А. Д. Перцептивные взаимодействия…

269

50 испытуемых приняли участие в эксперименте, проведенном нами для определения коэффициента константности видимой формы. Испыту­емому с расстояния полутора метров предъявлялись два прямоугольни­ка: эталонный и измеритель. Эталонный прямоугольник имел равные ширину и высоту (100 х 100 мм) и предъявлялся всегда наклоненным на угол а. Его размеры в течение всего эксперимента не менялись. Прямоу­гольник-измеритель, напротив, всегда имел одну и ту же ориентацию, но мог изменить свою форму: его высота могла уменьшаться или увеличи­ваться. Испытуемому предоставляли возможность управлять изменени­ем высоты прямоугольника-измерителя и просили подобрать для него такую высоту, чтобы его видимая форма была идентична видимой фор­ме наклоненного прямоугольника-эталона. Иными словами, методом ус­тановки¹ определялась точка субъективного равенства высоты наклонен­ного квадрата-эталона и фронтально расположенного прямоугольника-измерителя. Поскольку различие между формами эталона и измерителя в основном сводилось к различию по высоте, то это различие и было взя­то в качестве количественной меры различия по форме. Коэффициент константности в этом случае можно определить по такой формуле:


k = V-P/R-P


где R— высота прямоугольника-эталона; Р — проекционная высота пря­моугольника-эталона. Если а — угол наклона эталона, то Р = R-cosa; V— высота прямоугольника-измерителя, при которой он воспринимает­ся идентичным по форме прямоугольнику-эталону.

Поясним смысл этой формулы. Поскольку сетчаточная форма фрон­тально расположенного прямоугольника-измерителя совпадает с его фи­зической формой (нет наклона, следовательно, нет перспективных иска­жений и нет поэтому рассогласования между формой дистального и про­ксимального стимулов), то его видимая форма идентична физической форме. А поскольку по инструкции испытуемый должен был подравнять видимую форму измерителя к видимой форме эталона, то физическая форма измерителя идентична не только видимой форме измерителя, но и видимой форме эталона, поэтому она входит в формулу как видимая форма эталона V. Таким образом, в числителе формулы стоит разность между соответствующими параметрами видимой и проекционной форм эталона, т.е. величина компенсации перспективных искажений, которую реально осуществила зрительная система. В знаменателе — разность меж­ду соответствующими параметрами реальной и проекционной форм эта­лона, т.е. требуемая компенсация. Значит, это действительно отношение Брунсвика — Таулесса. <...>

¹ См.: GuilfordJ.P. Psychometric Methods. Bombay-New Delhi: Tata McGraw-Hill Publishing Co, 1954.

270

Тема 17. Экспериментальные исследования восприятия

Инвариантные соотношения в восприятии

Явление константности в зрительном восприятии свидетельствует о том, что проксимальный стимул не является единственной детерминантой для зрительного образа, который скорее соответствует дистальному сти­мулу, нежели проксимальному. А это в свою очередь означает, что в зри­тельном восприятии пространства существуют явления, которые не укла­дываются в обычную психофизическую логику: дистальный стимул —> проксимальный стимул —» зрительный образ. Первая стрелка описыва­ет физическое соотношение дистального и проксимального стимулов, вто­рая — психофизическую связь между стимулом и образом. В этом месте будет полезно сделать более гибкой используемую терминологию. Стимул и образ — это слишком глобальные понятия. Мы будем говорить дис­тальный параметр стимула (например, физическая величина), прокси­мальный параметр (зрительный угол) и феноменальный параметр обра­за (видимая величина). Явление константности, например, константность видимой глубины, показывает, что феноменальный параметр образа (ви­димая глубина) может детерминироваться не только соответствующим проксимальным параметром стимула, т.е. диспаратностью, но и некото­рым другим феноменальным параметром (видимой удаленностью). Еще одной иллюстрацией этого положения может служить так называемая комната Эймса¹. В плане эта комната имеет вид трапеции. Если два одинаковых по росту человека встанут вдоль задней стенки по углам, то угловая величина одного из них (того, который в дальнем углу) будет вдвое меньше угловой величины другого. Демонстрация Эймса состоит в том, что с помощью специально подобранных признаков удаленности создается иллюзия того, что комната имеет обычную прямоугольную форму, т.е. видимая удаленность этих стоящих по разным углам людей одинакова. Феномен состоит в том, что человек, находящийся в дальнем углу, кажется вдвое меньшим.

Наиболее интересным в этой демонстрации является то, что види­мая величина не просто изменилась, а уменьшилась ровно во столько раз, во сколько раз уменьшилась видимая дистанция. Это позволило Эймсу и его сотрудникам сформулировать принцип, согласно которому зритель­ный угол детерминирует не видимую величину, а отношение видимой величины к видимой удаленности. Этот же принцип Эймса формулиру­ют еще и так: при неизменной величине зрительного угла отношение видимой величины к видимой удаленности остается неизменным или, как иногда говорят, инвариантным. Любой из феноменальных параметров, входящих в инвариантное отношение, может измениться, как это случи-

¹ См.: Ittelaon W.H. The Ames Demonstrations in Perception. Princeton: Princeton University Press, 1952.

ЛогвиненкоА.Д. Перцептивные взаимодействия...

271

лось, например, в комнате Эймса, но при этом неизбежно произойдет изменение и другого феноменального параметра.

Следует подчеркнуть, что за утверждением о существовании в вос­приятии инвариантных отношений (или более сложных соотношений) лежит логика, принципиально отличная от психофизической. В психо­физическом подходе, например, видимая удаленность считается функци­ей от некоторых параметров проксимального стимула. В принципе Эйм­са же утверждается, что видимая удаленность является функцией не только от параметров проксимального стимула, но и от других феноме­нальных параметров образа, например, от видимой величины. Можно сказать, что феноменальные параметры образа взаимодействуют. В даль­нейшем такой вид взаимодействий мы будем называть перцептивными взаимодействиями.

Инвариантность отношения видимой величины и видимой удаленности

Этот вид инвариантного соотношения, на существование которого, пожалуй, впервые указал Коффка¹, наиболее исследован. Его можно выра­зить следующей простой формулой: проксимальная величина стимула (т.е. зрительный угол) однозначно определяет отношение видимой величины и видимой удаленности. В дальнейшем параметры дистального стимула бу­дем обозначать большими латинскими буквами, например, S— физичес­кая величина объекта; D— физическая удаленность объекта от наблюда­теля; D — физическая относительная удаленность объектов. Соответству­ющие им феноменальные параметры образа будем обозначать этими же буквами, но с чертой сверху, например, — видимая величина предмета; — видимая абсолютная удаленность; D— видимая относительная уда­ленность. Буквы греческого алфавита будем использовать для обозначения параметров проксимального стимула. Напомним уже встречавшиеся у нас обозначения: — зрительный угол (проксимальная величина объекта); у— конвергенционный угол; — диспаратность. В этих обозначениях ин­вариантность отношения «видимая величина — видимая удаленность» может быть выражена следующей формулой: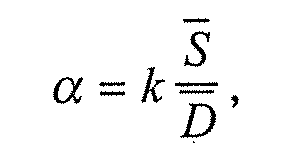




где k— коэффициент пропорциональности.

¹ См.: Koffka К. Principles of Gestalt Psychology. N. Y.: Hareourt, Brace, 1935.

272

Тема 17. Экспериментальные исследования восприятия

Легко убедиться в том, что изменение видимой величины объекта в комнате Эймса происходит в полном соответствии с этой формулой. Были проведены многочисленные исследования, в которых проверялось выполнение инвариантности отношения «видимая величина — видимая удаленность»¹. Экспериментальной проверке зачастую подвергалась не сама формула, а различные ее следствия.

Одним из следствий формулы является утверждение о том, что види­мая величина предмета пропорциональна етдимой удаленности, если про­ксимальная величина стимула постоянна: Убедить­ся в справедливости этого утверждения не просто, поскольку при прибли­жении объекта к наблюдателю происходит не только уменьшение видимой удаленности, но и увеличение зрительного угла. Проверить это утверждение можно лишь в лабораторном эксперименте, сохраняя посто­янным зрительный угол и изменяя расстояние до объекта. Такие экспе­рименты были проведены². Испытуемым предъявлялись стереограммы Юлеша и предлагалось оценить величину и относительную удаленность центрального квадрата. Физические размеры центрального квадрата и со­ответственно его зрительный угол сохранялись постоянными, в то время как диспаратность и соответственно видимая удаленность варьировались. Была получена линейная зависимость видимой величины от видимой уда­ленности в полном согласии со следствием из формулы.

Это же следствие можно проверить по-иному, используя послеобра-зы, сетчаточная величина которых неизменна. Будет ли изменяться ви­димая на экране величина послеобраза пропорционально расстоянию до экрана? Оказывается, да. Исследования, проведенные Эммертом, позво­лили ему сформулировать правило, названное впоследствии законом Эммерта: величина послеобраза пропорциональна его абсолютной удален­ности. Более поздние исследования показали, что речь идет именно о видимой удаленности послеобраза.

Второе следствие из инвариантности отношения видимая величина — видимая удаленность можно извлечь из формулы, положив При постоянной видимой удаленности видимая величина должна изменяться прямо пропорционально зрительному углу, т.е. S=ka, если . В этом следствии нетрудно узнать сформулированный выше закон угла зре­ния, или явление аконстантности величины.

В рамках концепции перцептивных взаимодействий находит свое объяснение аконстантность восприятия при редукции зрительных призна-

¹ См.: Kilpatrick F.P., Ittelson W.H. The size-distance invariance hypothesis // Psychol.
Rev. 1953. Vol. 60. P. 223-231; Ittelson W.H. Visual space perception. N. Y.: Springer,
1960; Epstein W„ Park J., Casey A. The current status of the size-distance hypothesis //
Psychol. Bull. 1961. Vol. 58. P. 491-514.

² См.: Lawson R.B., GuUck W.L. Stereopsis and anomalous contour // Vision Res. 1967.
Vol. 7, P. 271-297; Flneman M.B. Facilitation of stereoscopic depth perceptionby a relative-
size cue in ambiguous disparity stereograms // J. Exp. Psychol. 1971. Vol. 90 (2). P. 215-221.

Логвиненко А. Д. Перцептивные взаимодействия...

273

ков. Было показано, что в етимульных ситуациях с редуцированными при­знаками возникают так называемые «тенденция к равноудаленности» и «тенденция к специфической удаленности»¹. Тенденция к специфической удаленности состоит в том, что при полной (насколько это возможно) редук­ции признаков человек воспринимает объекты расположенными на одной и той же удаленности от себя. Прямые субъективные оценки (в метрах) показывают, что эта специфическая удаленность составляет 1,5 : 2,5 м².

Тенденция к равноудаленности состоит в том, что при редукции признаков редуцируется видимая относительная удаленность, создается впечатление, что все объекты расположены как бы в одной плоскости³. Как указывает Годжел, вдервые обративший внимание на существование этих тенденций в нашем восприятии, это именно тенденции, а не зако­ны восприятия для пространства, полностью лишенного зрительных признаков, поскольку они проявляются и при наличии зрительных при­знаков. Проявление этих тенденций может заключаться в ослаблении эффективности зрительного признака⁴.

Из существования тенденций к равноудаленности и специфической удаленности следует, что в редуцированной стимульной ситуации воспри­нимаемая удаленность объектов будет иметь тенденцию быть постоянной. Следовательно, воспринимаемая величина будет иметь тенденцию воспри­ниматься аконстантно, что и имеет место в действительности.

Третье следствие из гипотезы инвариантности соотношения «види­мая величина — видимая удаленность» относится к случаям, в которых величина воспринимаемого объекта хорошо известна по прошлому опы­ту, а признаки удаленности редуцированы, т.е. Иначе говоря, если видимая величина воспринимаемого объекта извест­на, то видимая удаленность будет обратно пропорциональна углу зрения. Это положение было экспериментально доказано в классическом экспе­рименте с картами⁵. Испытуемым предъявлялись три игральные карты в условиях полной редукции признаков удаленности. Каждая карта по­мещалась на одном и том же физическом расстоянии от наблюдателя. Однако размеры карт были неодинаковы: одна была нормальной величи-

¹ См.: Gogel W.C The organization of perceived space // Psychol. Forsch. 1973. Vol. 36.
P. 195-247.

² См.: Gogel W.C. The effect of object familiarity on the perception of size and distance
// Quart. J. Exp. Psychol. 1969. Vol. 21. P, 239-247; Gogel W.C. The sensing of retinal size
// Vision Res. 1969. Vol. 9. P. 3-24.

³ См.: Gogel W.C. The tendency to see objects as equidistant and its reverse relation to
lateral separation // Psychol Monogr. 1956. Vol. 70. Wol. 411.

* См.: Gogel W.C, Brune H.L., Inaba K. A modification of a stereopsis adjustment by the equidistance tendency // USAMRL Report. 1954. Vol. 157. P. 1-11; Gogel W.C. The validity of the size-distance invariance hypothesis with cue reduction // Percept. & Psychophys. 1971. Vol. 9. P. 92-94.

^s См.: Ittelson W.H. Visual space perception. N. Y.: Springer, 1960.

274

Тема 17. Экспериментальные исследования восприятия

ны, другая — вдвое больше, а третья — вдвое меньше обычной. Испыту­емые оценивали удаленность этих карт. Согласно гипотезе инвариантно­сти, большая карта должна быть локализована в два раза ближе, а мень­шая — в два раза дальше нормальной карты. Результаты эксперимента находились в полном соответствии с гипотезой инвариантности.

Еще одно следствие из инвариантности отношения «видимая величи­на — видимая удаленность» состоит в том, что при изменении зрительно­го угла видимая величина постоянна, если удаленность изменяется обрат­но пропорционально зрительному углу. Согласно данному следствию, ве­личина объекта будет восприниматься неизменной, если наблюдатель верно воспринимает изменение физического расстояния до объекта, т.е. воспринимает увеличение расстояния до объекта при уменьшении зритель­ного угла и уменьшение расстояния до него при увеличении зрительного угла. Но это и есть не что иное, как явление константности видимой вели­чины.

Вместе с тем существуют факты, указывающие на то, что инва­риантность отношения «видимая величина — видимая удаленность» иногда нарушается. Так, в опытах по оценке величины на разных удален-ностях обнаружена тенденция к возрастающей переоценке величины с увеличением физического расстояния до объекта. Из инвариантности от­ношения видимых величины и удаленности следует, что должна суще­ствовать аналогичная тенденция и для оценки удаленности. Однако на самом деле существует обратная тенденция: с удалением отрезки дистан­ции недооцениваются¹. Далее, в одних и тех же экспериментальных ус­ловиях может встретиться как недооценка видимой величины объекта при переоценке видимой удаленности, так и, наоборот, переоценка види­мой величины при недооценке видимой удаленности. И, наконец, в ряде ситуаций факторы, влияющие на один из параметров (величину или уда­ленность), не влияют на другие².

Прочие инвариантные соотношения в восприятии

[Ранее] упоминались инвариантные отношения, связывающие види­мую глубину и видимую удаленность: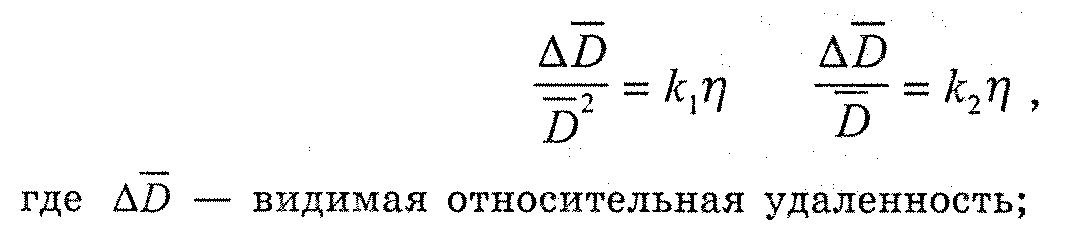


¹ См.: Gilinsky А. A.. Perceived size and distance in visual space // Psychol. Rev. 1951.
Vol. 58. P. 460-482.

² См.: Epstein, W., Park J., Casey A. The current status of the size-distance hypothesis //
Psychol. Bull. 1961. Vol. 58. P. 491-514.

Логвиненко А. Д. Перцептивные взаимодействия...

275

Смысл инвариантного соотношения состоит в том, что не только видимая абсолютная удаленность, но и видимая величина может опреде­лять видимую глубину.

Иногда перцептивные явления, лежащие в основе инвариантных соотношений, интерпретируют в терминах «шкалирования». Так, гово­рят, что видимая абсолютная удаленность шкалирует диспаратность. Имеется в виду, что видимая удаленность как бы задает шкалу, масш­таб для перевода диспаратности в видимую глубину. Если изменится масштаб, изменится и видимая глубина. В этой терминологии инвари­антное соотношение означает, что видимая величина может шкалировать диспаратность с таким же успехом, как и видимая абсолютная удален­ность.

Видимая абсолютная удаленность может шкалировать не только сетчаточную величину и диспаратность, но и сетчаточную скорость дви­жения. Было показано, что существует инвариантность отношения види­мых скоростей и абсолютной удаленности. Это отношение с точностью до коэффициента пропорциональности равно сетчаточной скорости².

Помимо приведенных инвариантных соотношений существует ряд экспериментальных фактов, указывающих на наличие других перцеп­тивных взаимодействий. Так, было показано, что разностные пороги вос­принимаемого движения определяются не сетчаточной, а видимой ско-

¹ См.: Gogel W.C. The perception of a depth interval with binocular disparity cues // J.
Psychol. 1960. Vol. 50. P. 257-269.

² См.: Rock I., Hill A.L., Flneman V. Speed constancy as a function of size constancy //
Percept. & Psychophys. 1968. Vol. 4. P. 37-40.

276

Тема 17. Экспериментальные исследования восприятия

ростью¹. Пороги стробоскопического движения определяются скорее не проксимальным пространственным интерстимульным интервалом, а ви­димым². Более того, наличие проксимального (сетчаточного) смещения в отсутствие видимого смещения вообще не вызывает стробоскопического эффекта³. Сила и продолжительность послеэффекта движения (спираль­ный послеэффект) монотонно возрастают с увеличением видимой удален­ности поля, на котором он наблюдается⁴.

¹ См.: Brown J.F. The thresholds for visual movement // Psychol. Forsch. 1931. Bd. 14,
S. 249-268; Brown J.F. The visu'al perception of velocity // Psychol. Forsch. 1931. Bd. 14.
S. 199-232.

² См.: Corbin H.H. The perception of grouping and apparent movement in visual depth //
Arch. Psychol. 1942. Vol. 273, P. 1-50; Attneave F., Block G. Apparent movement in
tridimensional space // Percept. & Psychophys. 1973. Vol. 13. P. 301-307.

³ См.: Rock D., Ebenholtz S. Stroboscopic movement based ore change of phenomenal location rather than retinal location // Am. J. Psychol. 1962. Vol. 75. P. 193-207.

⁴ См.: Williams MJ., Collins W.E. Some influence of visual angle and retinal speed on measures of the spiral aftereffects // Perceptual and Motor Skills. 1970. Vol. 30. P. 215-227; Mehling K.D., Collins W.E., Schroeder D.J. Some effects of perceived size, retinal size and retinal speed en duration of spiral aftereffect // Perceptual and Motor Skills. 1972. Vol. 34. P. 247-259.