еееее. Учебнометодическое пособие к лабораторнопрактическим занятиям по дисциплине Введение в информационные технологии для студентов направления подготовки 44. 03. 04 Профессиональное обучение всех форм обучения
 Скачать 1.6 Mb. Скачать 1.6 Mb.
|
Вопросы для защиты работыНазвать и охарактеризовать основные типы диаграмм. Описать процесс создания диаграмм. Дать определение понятиям “Ряд данных” и “категория данных”. Описать синтаксис и правила использования логических функций. Что такое макрос? Как записать макрос? Лабораторная работа №6. Электронные таблицы MS Excel: работа с матрицамиЦель работы: Научиться приемам работы с матрицами. Задачи лабораторной работы После выполнения работы студент должен: знать приемы работы с матрицами; уметь решать системы линейных алгебраических уравнений; уметь выполнять проверку решения. Перечень обеспечивающих средств Для обеспечения выполнения работы необходимо иметь компьютер со следующим обеспечением: операционная система Windows и MS Office 2007 и выше. Общие теоретические сведения Система mn чисел, расположенных в прямоугольной таблице из m строк и n столбцов, называется матрицей. Если m=n, то матрица называется квадратной, иначе прямоугольной. Над матрицами могут быть выполнены операции сложение матриц, умножение матрицы на число, на вектор. Если матрица имеет размер 1 x n, то она называется вектором-строкой, а m x 1 – вектором-столбцом. Если в матрице переставить строки и столбцы местами, то получим транспонированную матрицу. Обратной матрицей по отношению к данной, называется матрица, которая, будучи умноженной как справа, так и слева на данную матрицу, дает единичную матрицу. При умножении матриц результирующая матрица имеет такое количество строк, как матрица слева, а количество столбцов как матрица справа. Для освоения методов работы с матрицами рассмотрим пример. Пример 1. Умножить матрицу А2,3 на матрицу В3,3 и получить матрицу С2,3. 1. Задать значения элементам матриц A2,3, В3,3.
2. Выделить место для результирующей матрицы С2,3. 3. В строку формул записать знак равно (=). 4. С помощью мастера функций найти функцию МУМНОЖ. 5. Задать для нее исходные данные (указать с помощью мыши адреса матриц А и В). 6. Активизировать строку формул. 7. Нажать 3 клавиши Ctrl+Shift+Enter. 8. В результирующей матрице получим результат (рис. 1). 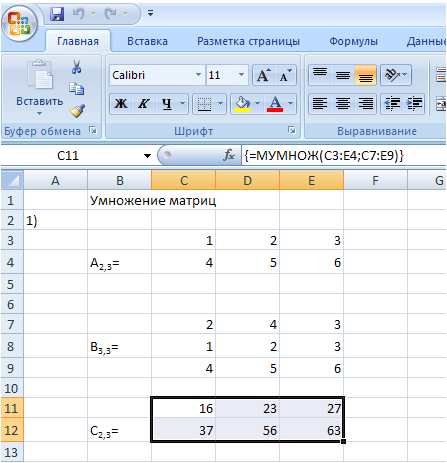 Рис. 1. Результат перемножения матриц Пример 2. Решение системы линейных алгебраических уравнений. Задана система линейных уравнений (1) x1+2•x2+3•x3 = 4 4•x1+3•x2+2•x3=1 (1) x1+3•x2+2мx3 = 4 В матричной форме система (1) имеет вид А3,3 • Х3,1 =В3,1 (2), где А3,3-матрица коэффициентов при неизвестных  B3,1 – вектор правых частей. Вектор неизвестных Х3,1 может быть найден по формуле Х3,1=А3,3-1 • В3,1 (5) А3,3-1 – обратная матрица. 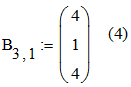 Решение задачи выполнить в таблице.
1. Ввести в таблицу значения матрицы коэффициентов А3,3. 2. Ввести в таблицу значения вектора В3,1. 3. Выделить место для обратной матрицы А3,3-1. 4. Вызвать мастер функций, отыскать функцию МОБР для вычисления обратной матрицы. 5. Ввести в диалоговое окно параметров функции адрес исходной матрицы коэффициентов мышью. Проверить записанный адрес. Если все нормально, щелкнуть мышью по строке формул (в ней появится курсор) и нажать 3 клавиши одновременно Ctrl+Shift+Enter. В выделенных ячейках появятся значения обратной матрицы. 6. Выделить место для результата (вектор неизвестных) Х3,1. 7. С помощью мастера функций найти функцию МУМНОЖ. 8. Ввести в диалоговое окно два адреса: адрес обратной матрицы (массив1); адрес вектора правых частей (массив2). 9. Активизировать строку формул, чтобы в ней появился курсор и нажать клавиши Ctrl+Shift+Enter (рис. 2). 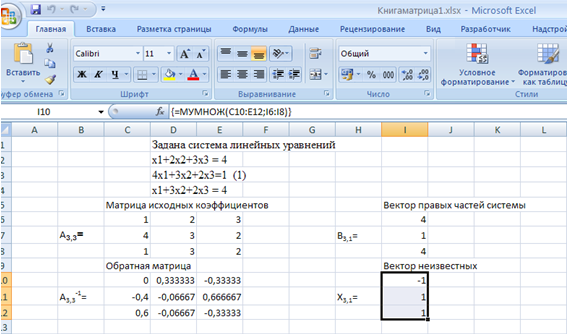 Рис. 2. Решение системы линейных алгебраических уравнений Пример 3. Решение системы линейных алгебраических уравнений методом Крамера (через определители). Работа со склеенными листами. Если данные для каких-то таблиц повторяются, то их лучше набирать в режиме «склеенных листов». Можно склеивать подряд стоящие листы, не подряд стоящие или вообще все листы рабочей книги. Пусть необходимо склеить три подряд стоящих листа (Лист1, Лист2, Лист3). Для этого производим щелчок левой кнопки мыши по ярлычку Лист1, затем нажимаем клавишу Shift и производим щелчок по ярлычку Лист3. Тогда все три ярлычка станут светлее. Чтобы расклеить листы, выполнить щелчок правой кнопкой мыши по ярлычку Лист1 и выбрать команду Разгруппировать листы. Для выполнения задания склеим 4 листа. Матрицу исходных коэффициентов и вектор правых частей поместить на склеенные листы. Затем расклеить листы. На листах 2, 3, 4 столбцы при неизвестных заменить векторами правых частей для вычисления определителей неизвестных: на листе2 в 1-ый столбец, на листе3 во 2-ой столбец и на листе4 в третий столбец. Вычислить определители на каждом листе, используя функцию МОПРЕД. Для вычисления значения неизвестных разделить определитель для соответствующей переменной на общий определитель для матрицы исходных коэффициентов, так для вычисления х1 разделить определитель на листе2 на определитель на листе1, для х2 – определитель на листе3 на определитель на листе1 и т. д. Ввод формул выполнять только в строку формул. С дополнительным материалом по теме можно ознакомиться в литературе [1, 3, 4, 7]. Задание | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
