Учебное пособие для студентов высших учебных заведений очного и заочного обучения
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
|
Условия равновесия системы сходящихся сил Ранее было отмечено, что при равновесии система сил эквивалентна нулю. Поскольку любая система сходящихся сил имеет равнодействующую (заменяется одной силой), следовательно, для равновесия системы сходящихся сил необходимо и достаточно, чтобы ее равнодействующая была равна нулю (R = 0). В геометрической форме это значит, что многоугольник, построенный из сил системы должен быть замкнутым. В аналитической форме равенство нулю равнодействующей будет при равенстве нулю сумм проекций всех сил системы на оси координат (1). Таким образом, для равновесия сходящейся системы сил в пространстве необходимо и достаточно, чтобы суммы проекций всех сил системы на оси x, y, z были равны нулю: 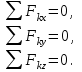 (2) (2)Для равновесия же системы сходящихся сил на плоскости необходимо и достаточно, чтобы суммы проекций всех сил системы на оси x и y, расположенные в той же плоскости что и силы системы, были равны нулю: 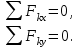 (3) (3)То есть, плоскостная и пространственная модели систем координат отличаются по количеству равенств и по количеству осей системы. Момент силы относительно точки (алгебраический и как вектор) Вращательное действие силы относительно точки (оси) оценивается ее моментом. Различают алгебраический момент силы относительно точки (для краткости слово алгебраический часто опускается) и момент силы относительно точки, как вектор. Моментом силы относительно точки называется взятое со знаком плюс или минус произведение модуля силы на ее плечо. 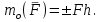 Плечом h называется наименьшее расстояние от точки до линии действия силы (рисунок 2).  Рисунок 2 – Плечо силы h Момент (в теоретической механике) считается положительным тогда, когда сила стремится повернуть тело против хода часовой стрелки, и отрицательным, если по ходу часовой стрелки. Заметим, что с геометрической точки зрения 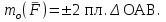 Рассмотренным алгебраическим моментом силы пользуются тогда, когда все силы системы и точка О лежат в одной плоскости (моменты имеют одну плоскость действия). Когда же плоскости действия моментов сил разные, то их необходимо учитывать, поскольку вращательное действие силы относительно неподвижной точки определяется не только модулем момента (Fh) и направлением вращения, но и плоскостью действия момента (она проходит через вектор силы и точку). В этом случае момент силы представляют вектором, приложенным в данной точке, расположенным перпендикулярно плоскости действия момента и направленным от этой плоскости в ту сторону, откуда поворот силы виден против хода часовой стрелки (Рисунок 3). 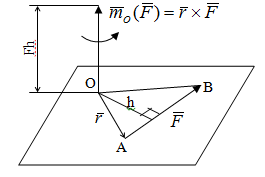 Рисунок 3 – Направление вектора момента силы Такой вектор задает и плоскость действия момента, и модуль момента, и направление вращения. Остановимся на выражении вектор-момента силы относительно точки векторным произведением радиус-вектора 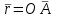 и вектора силы и вектора силы 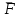 . Как отмечалось выше момент силы относительно точки О равен удвоенной площади треугольника ОАВ. С другой стороны . Как отмечалось выше момент силы относительно точки О равен удвоенной площади треугольника ОАВ. С другой стороны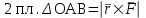 , ,то есть векторы 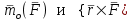 равны по модулю. равны по модулю.Если исходить из определения векторного произведения двух векторов, что это есть вектор расположенный перпендикулярно к перемножаемым векторам и направленный туда, откуда поворот первого вектора ко второму на наименьший угол виден против хода часовой стрелки, по рисунку 3 можно увидеть, что векторы 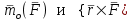 совпадают по направлению. Тогда получается, что совпадают по направлению. Тогда получается, что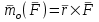 (4) (4)Таким образом, равенство является актуальным и доказывается даже по чертежу. Теорема Вариньона о моменте равнодействующей Дадим обобщенную формулировку теоремы (без доказательства): момент равнодействующей системы сил относительно точки или оси равен сумме моментов всех сил системы относительно этой точки или оси. Условие равновесия рычага Под рычагом в механике понимается любое тело, которое может поворачиваться вокруг некоторой точки или оси под действием активных сил. Рассмотрим рычаг (Рисунок 4), на который действуют активные силы 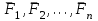 . .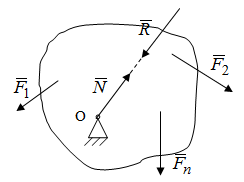 Рисунок 4 – Рычаг и активные силы Приведем эту систему сил к равнодействующей 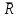 . Тогда на рычаг будут действовать две силы – равнодействующая . Тогда на рычаг будут действовать две силы – равнодействующая 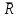 и реакция и реакция 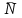 опоры (оси) О рычага. При равновесии рычага эти силы будут равны по модулю и направлены вдоль одной прямой в противоположные стороны (согласно аксиомы 1 статики). Из этого следует, что момент равнодействующей активных сил системы относительно точки опоры (оси) рычага будет равен нулю, так как линия действия равнодействующей будет проходить через О. Последний же, согласно теоремы Вариньона о моменте равнодействующей, равен сумме моментов всех активных сил системы относительно точки опоры (оси) рычага. То есть: опоры (оси) О рычага. При равновесии рычага эти силы будут равны по модулю и направлены вдоль одной прямой в противоположные стороны (согласно аксиомы 1 статики). Из этого следует, что момент равнодействующей активных сил системы относительно точки опоры (оси) рычага будет равен нулю, так как линия действия равнодействующей будет проходить через О. Последний же, согласно теоремы Вариньона о моменте равнодействующей, равен сумме моментов всех активных сил системы относительно точки опоры (оси) рычага. То есть: Полученное равенство является условием равновесия рычага: для равновесия рычага необходимо и достаточно, чтобы сумма моментов всех активных сил, действующих на рычаг, относительно точки опоры (оси) рычага была равна нулю. Момент силы относительно оси Рассмотрим тело в виде прямоугольной пластины, которое может поворачиваться вокруг оси z под действием силы 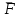 (Рисунок 5). (Рисунок 5).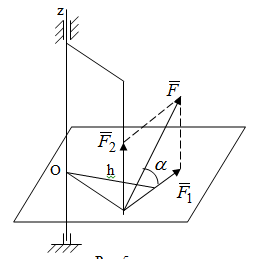 Рисунок 5 – Момент силы относительно точки Разложим эту силу на две составляющие 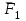 , лежащую в плоскости перпендикулярной оси z, и силу , лежащую в плоскости перпендикулярной оси z, и силу 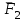 параллельную этой оси. Согласно теореме Вариньона о моменте равнодействующей момент силы параллельную этой оси. Согласно теореме Вариньона о моменте равнодействующей момент силы 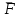 относительно оси z будет равен сумме моментов сил относительно оси z будет равен сумме моментов сил 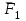 и и 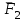 относительно этой оси: относительно этой оси: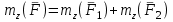 . .Момент силы 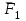 будет равен: будет равен: 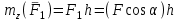 , а момент , а момент 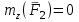 , так как она параллельна оси z и повернуть тело вокруг оси не может, что вполне очевидно. Тогда окончательно получим , так как она параллельна оси z и повернуть тело вокруг оси не может, что вполне очевидно. Тогда окончательно получим Таким образом, для определения момента силы относительно оси необходимо силу спроектировать на плоскость перпендикулярную оси и найти момент этой проекции относительно точки пересечения этой плоскости с осью. Момент считается положительным, если глядя с положительного конца оси видят поворот, совершаемый силой, против хода часовой стрелки, и отрицательным, если по ходу часовой стрелки. Обратим внимание на то, что если сила параллельна оси или линия ее действия пересекает ось, то ее момент относительно оси будет равен нулю. Связь момента силы относительно оси с моментом силы относительно любой точки на оси Покажем на чертеже ось z, силу 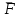 , вектор-момент этой силы относительно произвольной точки О на оси, проекцию этой силы , вектор-момент этой силы относительно произвольной точки О на оси, проекцию этой силы 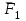 на плоскость перпендикулярную оси z, треугольники ОАВ и Оab, удвоенные площади которых равны соответственно моменту силы относительно точки о и моменту силы относительно оси z (Рисунок 6). на плоскость перпендикулярную оси z, треугольники ОАВ и Оab, удвоенные площади которых равны соответственно моменту силы относительно точки о и моменту силы относительно оси z (Рисунок 6).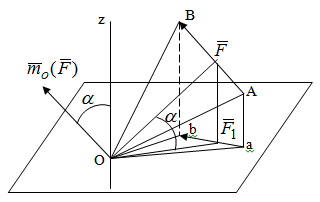 Рисунок 6 – Взаимосвязь моментов сил Учитывая, что 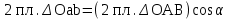 тогда окончательно получим: 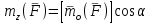 . .Это равенство показывает, что момент силы относительно оси равен проекции на эту ось вектор-момента силы относительно любой точки на этой оси. Аналитические формулы момента силы относительно координатных осей Как было установлено выше, вектор-момент силы относительно точки равен: 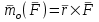 Выразим векторное произведение 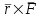 через проекции этих векторов на оси координат: через проекции этих векторов на оси координат: где x, y z – проекции радиус-вектора 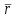 на координатные оси и они же координаты точки приложения силы. на координатные оси и они же координаты точки приложения силы.Учитывая, что проекция вектор-момента силы относительно точки на оси на ось равна моменту силы относительно оси, из полученного равенства следует, что моменты силы 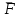 относительно координатных осей равны: относительно координатных осей равны: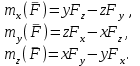 Данные равенства называются аналитическими формулами момента силы относительно координатных осей. Лекция 2 Связи и их реакции. Виды связей и направление их реакций. Аксиома связей. Пара сил. Момент пары алгебраический и как вектор. Теорема об эквивалентных парах на плоскости. Свойства пар на плоскости. Теорема о переносе пары в параллельную плоскость. Теоремы о сложении пар на плоскости и в пространстве. Условия равновесия пар на плоскости и в пространстве. Связи и их реакции Все твердые тела можно разделить на свободные и несвободные. Свободным называется тело, которому из данного положения можно сообщить перемещение в любом направлении в пространстве. Несвободными называются тела, перемещение которых по какому-либо направлению ограничено другими телами. Все ограничения (тела), препятствующие перемещению данного тела в пространстве по какому-либо направлению, называются связями. Силы, с которыми связи действуют на данное тело, называются реакциями связей. В дальнейшем силы, не являющиеся реакциями связей, будем называть активными силами. Их направление и численная величина не зависят от других действующих на тело сил и от наложенных на него связей. Реакции же связей, наоборот, зависят от активных сил полностью. Виды связей и направление их реакций Для решения задач механики очень важно знать виды связей и направление их реакций. Рассмотрим основные виды связей: Опора на гладкую поверхность. Под гладкой понимается поверхность, трением о которую пренебрегают. Такая поверхность не дает телу перемещаться по направлению по перпендикулярному к ней направлению. Поэтому, реакция N гладкой поверхности направлена перпендикулярно от этой поверхности (Рисунок 1).  Рисунок 1 – Реакция опоры гладкой поверхности Нить. Связью служит гибкая нерастяжимая нить. Практически к этому виду связи относятся все гибкие тела: ремни, цепи, тросы, канаты, веревки и другие. Реакция нити всегда направлена вдоль нити к точке ее подвеса (Рисунок 2). 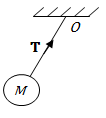 Рисунок 2 – Вид связи нить Стержень. Это жесткое длинное тело АВ с шарнирами на концах, сечение которого мало по сравнению с его длиной. Трением в шарнирах и весом стержня обычно пренебрегают, тогда он работает или на сжатие, или на растяжение. Поэтому реакция стержня всегда направлена вдоль стержня. Направление ее наперед неизвестно и если показано будет не то направление, то перед значением реакции получим знак минус (Рисунок 3).  Рисунок 3 – Стержень Неподвижный цилиндрический шарнир (подшипник). По конструкции они могут быть самые разнообразные, простейший пример – две тела соединенные круглым прутком, проходящим через отверстия в этих телах. Осевая линия z прутка называется осью шарнира. Условные изображения такого шарнира А показаны на рисунке 4. Так как шарнир не препятствует движению тела (прутка) вдоль оси шарнира, а ограничивает его перемещения по любому направлению перпендикулярному этой оси, то реакция неподвижного цилиндрического шарнира направлена перпендикулярно его оси, но в каком направлении неизвестно наперед. Поэтому, в большинстве случаев, ее наугад задают двумя составляющими (например 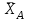 , , 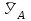 , как на рисунке 4) параллельными осям координат, которые к оси шарнира располагают перпендикулярно. Правильность выбора направления этих составляющих уточняется по завершении их вычисления: если направления показаны верно, то значения составляющих будут иметь знаки плюс, а если нет, то знаки минус. Модули же составляющих будут верны и от того угадали мы или нет направления составляющих не зависят. , как на рисунке 4) параллельными осям координат, которые к оси шарнира располагают перпендикулярно. Правильность выбора направления этих составляющих уточняется по завершении их вычисления: если направления показаны верно, то значения составляющих будут иметь знаки плюс, а если нет, то знаки минус. Модули же составляющих будут верны и от того угадали мы или нет направления составляющих не зависят.Когда на тело действует не более трех сил, включая реакции связей, и они расположены в одной плоскости и не параллельны, то направление (точнее линию действия) реакции неподвижного цилиндрического шарнира определяют с помощью теоремы о трех силах. Она состоит в следующем: если на тело, находящееся в равновесии, действуют три непараллельные силы, лежащие в одной плоскости, то линии их действия пересекаются в одной точке.  Рисунок 4 – Неподвижный цилиндрический шарнир или подшипник Шаровой шарнир и подпятник. Направления реакций этих связей наперед неизвестны, так как они ограничивают перемещение тела по всем направлениям. Поэтому их реакцию задают тремя составляющими параллельными осям координат x, y, z и по полученным знакам этих величин судят о правильности указания направлений составляющих. Жесткая заделка. В этом случае часть тела, например конец балки, вмонтирована в другое тело (связь) жестко – замурована в кладку, залита бетоном, запрессована в отверстие, ввинчена в резьбовое отверстие и т.п. При действии на тело плоской системы сил реакция жесткой заделки будет состоять из произвольной плоской системы сил, которая приводится к силе и паре, с неизвестными наперед направлениями. Поэтому реакцию жесткой заделки задают двумя составляющими параллельными осям х и у, расположенными в плоскости действующих на тело сил, и парой сил, расположенной в той же плоскости (Рисунок 5).  Рисунок 5 – Жесткая заделка балки Направления составляющих и вращения пары указывают произвольно и уточняют по завершении их определения по полученным знакам их значений. Аксиома связей. Эта аксиома состоит в следующем: любое не свободное тело можно сделать свободным, если отбросить связи и их действие заменить реакциями. Пара сил. Момент пары алгебраический и как вектор Парой сил называется система из двух равных по модулю антипараллельных сил. Пара равнодействующей не имеет, т. е. заменить и уравновесить ее одной силой нельзя. Пара оказывает вращательное действие, которое определяется тремя факторами: модулем момента пары, направлением вращения, плоскостью действия пары (та плоскость, в которой лежат силы пары). Различают алгебраический момент пары и момент пары как вектор. Моментом пары (алгебраическим) называется взятое со знаком плюс или минус произведение модуля любой из сил пары на плечо пары.  Плечо h – это наименьшее расстояние между линиями действия сил пары. Знак учитывает направление вращения пары: если пара стремится вращать тело против хода часовой стрелки, то ее момент принято считать положительным, а если по ходу часовой стрелки, то отрицательным. На чертежах пары чаще изображают дуговыми стрелками с указанием их момента. Заметим, что с геометрической точки зрения момент пары равен удвоенной площади треугольника, одной стороной которого является любая сила пары, а двумя другими отрезки, соединяющие начало и конец вектора этой силы с точкой приложения второй силы пары, например  (Рисунок 6). (Рисунок 6).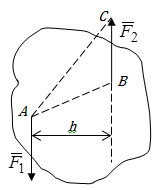 Рисунок 6 – Момент пары сил Алгебраическим моментом пары пользуются тогда, когда пары лежат в одной плоскости, а поэтому задавать ее не надо. Если же пары имеют разные плоскости действия, то надо учитывать плоскости их действия, и тогда момент пары представляют вектором. Этот вектор-момент пары, численно равный модулю момента пары, прилагают в любой точке плоскости действия пары и направляют его перпендикулярно от этой плоскости туда, откуда поворот пары виден против хода часовой стрелки (Рисунок 7). 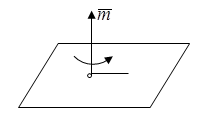 Рисунок 7 – Вектор-момент пары сил Такой вектор один задает все три, упомянутые выше, фактора, определяющие действие пары. |
