Учебное пособие для студентов высших учебных заведений очного и заочного обучения
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
|
Частные случаи движения точки. Прямолинейное движение точки. В этом случае радиус кривизны траектории равен бесконечности, поэтому нормальное ускорение равно нулю и полное ускорение точки равно ее касательному ускорению. В этом случае скорость изменяется только по модулю, следовательно, касательное ускорение точки характеризует изменение скорости по модулю. Заметим, что нормальное ускорение точки равно нулю еще и в точках перегиба ее траектории, поскольку в них радиус кривизны траектории бесконечно большой. Равномерное криволинейное движение. В этом случае модуль скорости точки постоянен. Поэтому касательное ускорение точки равно нулю. Полное ускорение точки равно ее нормальному ускорению. Так как в этом случае скорость изменяется только по направлению, то, следовательно, нормальное ускорение точки характеризует изменение скорости по направлению. Равномерное прямолинейное движение. В этом случае и нормальное, и касательное, а, следовательно, и полное ускорения точки равны нулю. Это единственный частный случай, при котором ускорение точки равно нулю. Равнопеременное движение. Равнопеременным называется такое движение точки, при котором ее касательное ускорение постоянно. В этом случае точка движется согласно уравнения (закона) 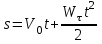 , ,а скорость точки 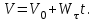 Если знаки скорости и касательного ускорения одинаковые, то точка движется равноускоренно, а если знаки разные, то точка движется равнозамедленно. Лекция 2 Поступательное движение твердого тела. Вращательное движение твердого тела. Основные определения и понятия, задание вращательного движения. Угловая скорость и угловое ускорение. Частные случаи вращательного движения тела. Линейная скорость точки вращающегося тела. Ускорение точки вращающегося тела. Формула Эйлера для линейной скорости точки вращающегося тела. Кинематические формулы Эйлера. Поступательное движение твердого тела Поступательным называется такое движение твердого тела, при котором любая прямая, проведенная в теле остается параллельной своему первоначальному положению. Такое движение совершают, например, педаль велосипеда; спарник АВ, соединяющий два кривошипа (рисунок 1). 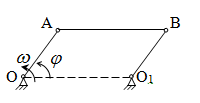 Рисунок 1 – Спарник При поступательном движении точки тела могут двигаться по любым траекториям, поэтому его нельзя смешивать с прямолинейным движением. Остановимся на задании поступательного движения тела. Пусть тело D движется поступательно относительно неподвижных осей координат Oxyz (рисунок 2). 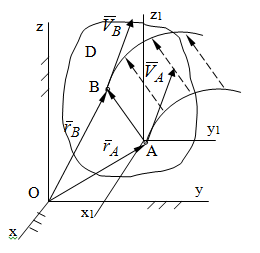 Рисунок 2 – Задание поступательного движения Возьмем в теле произвольную точку А и проведем через нее оси координат О1x1y1z1 жестко связанные с телом, расположив их параллельно осям x, y, z. Так как тело относительно осей, жестко с ним связанных, занимает неизменное положение, то его положение относительно неподвижных осей координат Oxyz в любой момент времени определяется положением подвижных осей координат. А их положение, поскольку они будут всегда параллельны неподвижным осям, можно определить по положению точки А – началу этой системы координат. Отсюда следует, что положение тела при поступательном движении можно определить по положению одной любой его точки, движение которой можно задать координатным, естественным или векторным способом. Возьмем еще одну произвольную точку В тела. Положение точек А и В будем определять их радиус-векторами 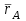 и и 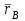 . Соединим точку А с точкой В вектором . Соединим точку А с точкой В вектором 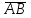 (заметим, что этот вектор постоянен по модулю и направлению). Тогда, как видим (рис. 2) (заметим, что этот вектор постоянен по модулю и направлению). Тогда, как видим (рис. 2)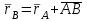 . (1) . (1)Из уравнения (1) вытекает, что траектория точки В получается смещением всех точек траектории точки А на постоянную величину 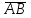 , то есть траектории всех точек тела будут одинаковыми, совпадающими при наложении. , то есть траектории всех точек тела будут одинаковыми, совпадающими при наложении.Теперь обе части равенства (1) продифференцируем дважды по времени, учитывая, что первая производная от радиус-вектора точки есть вектор ее скорости, а вторая производная- вектор ускорения точки, получим: 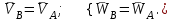 Из всего изложенного следует, при поступательном движении твердого тела все его точки движутся по одинаковым, совпадающим при наложении, траекториям и в каждый момент времени имеют одинаковые по модулю и направлению скорости и равные по модулю и направлению ускорения. Таким образом, для изучения этого движения тела достаточно изучить движение одной любой его точки. Вращательное движение твердого тела Вращательным называется такое движение твердого тела, при котором две его точки (или две неизменно связанные с ним точки) остаются неподвижными. Прямая, проходящая через эти точки называется осью вращения. Все точки тела, лежащие на оси вращения неподвижны, все остальные точки тела движутся по окружностям вокруг оси вращения. Плоскости этих окружностей перпендикулярны к оси вращения. Для задания вращательного движения тела проведем через ось его вращения две полуплоскости: неподвижную и жестко связанную с телом (врезанную в него) и вращающуюся вместе с ним (рисунок 3). 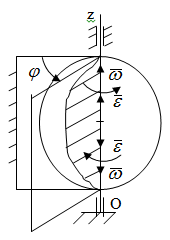 Рисунок 3 – Вращательное движение твердого тела Тогда положение тела в любой момент времени можно определить по углу 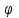 между этими полуплоскостями взятому с соответствующим знаком. Угол между этими полуплоскостями взятому с соответствующим знаком. Угол 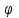 называется углом поворота тела. Измеряется он в радианах. С течением времени он непрерывно изменяется и, следовательно, является функцией времени: называется углом поворота тела. Измеряется он в радианах. С течением времени он непрерывно изменяется и, следовательно, является функцией времени: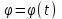 . .Это уравнение называется уравнением (законом) вращательного движения твердого тела. Угол 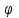 поворота тела принято считать положительным, если он образован вращением тела против хода часовой стрелки, и отрицательным, если вращением по ходу часовой стрелки. Направление вращения смотрят с положительного конца координатной оси, проведенной вдоль оси вращения тела. поворота тела принято считать положительным, если он образован вращением тела против хода часовой стрелки, и отрицательным, если вращением по ходу часовой стрелки. Направление вращения смотрят с положительного конца координатной оси, проведенной вдоль оси вращения тела.Угловая скорость и угловое ускорение вращающегося тела Угловая скорость 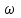 и угловое ускорение и угловое ускорение 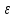 являются основными, общими для всех точек тела, кинематическими характеристиками вращательного движения тела. являются основными, общими для всех точек тела, кинематическими характеристиками вращательного движения тела. Если за время  угол поворота тела получил приращение угол поворота тела получил приращение 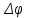 , то средняя угловая скорость тела за это время , то средняя угловая скорость тела за это время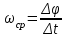 . .Для определения угловой скорости тела в данный момент времени возьмем предел от средней угловой скорости при 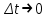 и получим и получим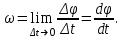 Таким образом, угловая скорость равна первой производной по времени от угла поворота тела: 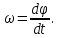 Единицей измерения угловой скорости являются радианы в секунду (1 рад/с). Угловая скорость, как и угол поворота, может иметь знак плюс или минус. Если она имеет знак плюс, то тело вращается против хода часовой стрелки, а если минус, то по ходу часовой стрелки (правило знаков то же, что и для угла поворота тела). Угловую скорость можно, а иногда и необходимо, изображать вектором. Вектор угловой скорости располагают на оси вращения и направляют туда, откуда поворот тела виден против хода часовой стрелки. Угловое ускорение характеризует быстроту изменения угловой скорости с течением времени. Если за время  угловая скорость изменилась на угловая скорость изменилась на 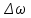 , то среднее угловое ускорение тела за это время будет , то среднее угловое ускорение тела за это время будет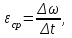 а перейдя к пределу среднего ускорения при 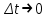 получим, что получим, что Следовательно, угловое ускорение тела равно первой производной по времени от его угловой скорости или второй производной по времени от угла поворота тела. Измеряется оно в радианах за секунду в квадрате (1 рад/с2) и может иметь знаки плюс или минус. На рисунках его направление следует показывать с учетом знака. Обратим внимание на то, что если знаки угловой скорости и углового ускорения будут одинаковые (совпадают), то вращение будет ускоренным, а если нет, то замедленным. По аналогии с угловой скоростью, угловое ускорение можно изображать вектором, который располагают на оси вращения тела и направляют с учетом его знака: при ускоренном вращении в сторону вектора угловой скорости, при замедленном – против вектора угловой скорости. Частные случаи вращательного движения тела Равномерное вращение. Равномерным называется такое вращение тела, при котором его угловая скорость постоянна. Следовательно при равномерном вращении тела его угловое ускорение равно нулю. Из формулы 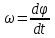 следует что 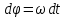 . .Интегрируя обе части этого дифференциального уравнения в соответствующих пределах получим закон равномерного вращения тела: 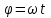 . .Отсюда угловая скорость тела при равномерном вращении  В технической практике угловая скорость равномерного вращения как правило задается не в 1/с, а частотой n вращения об/мин. Найдем зависимость между ними: 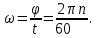 Следовательно 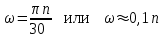 , ,что и требовалось доказать. Равнопеременное вращение. Равнопеременным называется такое вращение тела, при котором его угловое ускорение постоянно. При равнопеременном вращении угол поворота тела 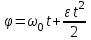 . .Это равенство есть уравнение (закон) равнопеременного вращения тела. Если обе части этого равенства продифференцируем по времени, то получим формулу угловой скорости тела при равнопеременном вращении 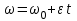 . .Если знаки угловой скорости и углового ускорения совпадают, то вращение будет равноускоренное, а если нет – равнозамедленное. Линейная скорость точки вращающегося тела Пусть в момент времени t произвольная точка вращающегося тела была в положении М, а в момент времени t1 переместилась в положение М1 (рисунок 4). 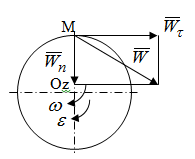 Рисунок 4 – Линейная скорость вращающегося тела Тогда расстояние пройденное точкой по дуге, описываемой ей окружности будет  . .Это равенство является уравнением движения точки вращающегося тела в естественной форме. Для определения скорости точки продифференцируем обе части этого равенства по времени: 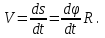 Учитывая, что 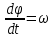 окончательно получим  . .Таким образом, линейная скорость точки вращающегося тела равна произведению его угловой скорости на расстояние от этой точки до оси вращения (радиус окружности, описываемой точкой). Направлена скорость точки по касательной к ее траектории в сторону вращения тела (рис. 4). Из полученной формулы видно, что скорости точек вращающегося тела пропорциональны их расстояниям до оси вращения. Ускорение точки вращающегося тела Ускорение точки вращающегося тела определяют по ее касательному и нормальному ускорениям, поскольку движение точки легко задается естественным способом: 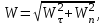 где  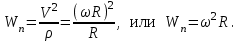 С учетом значений касательного и нормального ускорений формулу полного ускорения можно преобразовать к виду 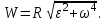 Из последней формулы следует, что ускорения точек вращающегося тела пропорциональны их расстояниям до оси вращения. Касательное ускорение точки направлено по касательной к ее траектории в сторону углового ускорения Нормальное ускорение точки всегда направлено к оси вращения тела по радиусу окружности, описываемой точкой. Направления ускорений показаны ранее. Формула Эйлера для линейной скорости точки вращающегося тела Покажем на чертеже вращающееся тело, вектор угловой скорости тела, некоторую произвольную точку М тела, ее радиус-вектор 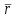 и скорость и скорость 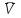 , расстояние R от точки М до оси вращения тела - радиус окружности, описываемой точкой (Рисунок 6). , расстояние R от точки М до оси вращения тела - радиус окружности, описываемой точкой (Рисунок 6).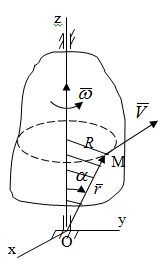 Рисунок 6 – Доказательство формулы Эйлера для линейной скорости точки вращающегося тела Выразим линейную скорость точки М: 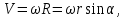 с другой стороны 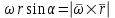 . .Следовательно, модуль линейной скорости точки вращающегося тела равен модулю векторного произведения угловой скорости и радиус-вектора точки: 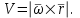 Кроме того, исходя из определения векторного произведения названных векторов и их расположения на рис. 6, направления линейной скорости точки (она перпендикулярна плоскости, проходящей через радиус-вектор и вектор угловой скорости) можно сделать вывод, что векторы 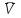 и и 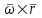 совпадают по направлению. совпадают по направлению.Из изложенного вытекает, что вектор линейной скорости точки вращающегося тела равен векторному произведению вектора угловой скорости тела и радиус-вектора этой точки относительно любой точки на оси вращения тела: 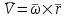 . .Эта формула называется формулой Эйлера для линейной скорости точки вращающегося тела. Кинематические формулы Эйлера Приведенная выше формула Эйлера позволяет вычислить линейную скорость точки вращающегося тела по ее проекциям на оси x, y, z жестко связанные с телом:  Для определения проекций скорости на координатные оси нужно векторное произведение 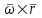 выразить через проекции этих векторов на оси координат. выразить через проекции этих векторов на оси координат.Разложим векторы 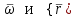 на составляющие по осям координат: на составляющие по осям координат: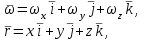 где x, y, z – координаты точки (они же проекции 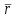 на оси координат). на оси координат).Тогда  Из этой формулы, разложения вектора скорости точки на составляющие по осям координат, следует, что проекции скорости точки вращающегося тела на оси координат равны: 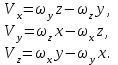 Эти формулы называются кинематическими формулами Эйлера. |
