Учебное пособие для студентов высших учебных заведений очного и заочного обучения

• Название: Учебное пособие для студентов высших учебных заведений очного и заочного обучения
• Дата: 05.03.2022
• Размер: 1.22 Mb.
• Имя файла: Met._ukazaniya_+_zadanie_Teoretich._mehanika__SHisteev_A.V._1580.docx
• Тип: Учебное пособие; #383430
• страница: 8 из 9

Лекция 3

1. 
   Метод кинетостатики для материальной точки
   
2. 
   Принцип Даламбера
   
3. 
   Работа и мощность.
   

Метод кинетостатики для материальной точки
Материальная точка, движение которой в пространстве не ограничено какими либо связями, называется свободной, а материальная точка, свобода которой ограничена, называется несвободной. Для несвободной материальной точки все внешние силы необходимо делить на две категории:

1. 
   Активные (в динамике движущие) силы
   
2. 
   Реакции связи (пассивные силы).
   

Если несвободную материальную точку освободить от связей и заменить связи их реакциями, то движение точки можно рассматривать, как свободное, а основному закону динамики придать вид: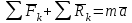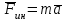



Силой инерции называется сила противодействия точки телу, которое вызвало ее движение. Она равна произведению массы точки на ускорение и направлена в сторонк противоположную ускорению.
Принцип Даламбера
Принцип Даламбера имеет несколько формулировок:

1. 
   Если к движущейся ускоренно материальной точке приложить, кроме действующих на нее активной силы и силы реакции связи еще и силу инерции, то точка приведется в состояние равновесия.
   
2. 
   Во время движения материальной точки сумма всех сил, действующих на нее, включая силу инерции, равна нулю.
   
3. 
   Силы, действующие на материальную точку, и сила инерции взаимно уравновешиваются.
   

Таким образом, в принципе Даламбера идет речь не об абсолютном равновесии, а о равновесии условном, воображаемом, поскольку добавление к действующим на точку силам инерции является искусственным приемом, так как фактически к данной точке эта сила не приложена, поскольку она приложена к телу, вызывающему ускоренное движение точки.
Для системы сил этот принцип можно сформулировать:

1. 
   Если к каждой точке механической системы, не находящейся в равновесии, приложить равнодействующую внешних сил, равнодействующую внутренних сил и силу инерции точки, то система приведется равновесное состояние.
   
2. 
   Если к каждой точке системы приложить кроме активной силы, силы реакции связи и силу инерции, то система приведется в состояние равновесия.
   

Метод решения задач динамики способами статики и кинематики, основанный на принципе Даламбера, называется методом кинетостатики.
Работа и мощность
Элементарная работа силы равна произведению касательной составляющей силы на элементарное перемещение точки ее приложения: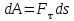
.
В зависимости от способа задания движения, элементарная работа силы также может быть выражена: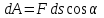


где α – угол между направлениями силы и скорости точки ее приложения.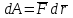


где - дифференциал радиус-вектора приложения силы.
,
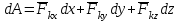где dx, dy, dz – элементарные перемещения точки приложения силы вдоль осей координат.
Работа оценивает действие только касательной составляющей силы, то есть составляющей, которая изменяет модуль скорости точки приложения силы.

Работа на конечном промежутке перемещения равна взятому вдоль этого перемещения интегралу от элементарной работы.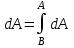


Выражения работы для некоторых видов сил:
1.Работа силы тяжести равна взятому со знаком плюс или минус произведению ее модуля на вертикальное перемещение точки ее приложения:

Таким образом, если точка приложения силы тяжести опускается, то работа силы тяжести положительная, а если поднимается, то отрицательная.
2.Работа силы упругости, например пружины, равна половине произведения коэффициента жесткости на разность квадратов ее начального и конечного растяжения от свободного состояния: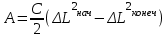


Она зависит только от начального и конечного положения точек их приложения, а силы обладающие такими свойствами называются потенциальными.

3.Работа силы при вращении тела вокруг неподвижной оси равна интегралу по углу поворота тела от произведения момента силы относительно оси вращения на элементарный угол поворота тела:



При этом, если M_z = const, то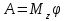


Мощностью называется отношение элементарной работы силы к элементарному промежутку времени, характеризующее быстроту приращения работы силы.

При поступательном движении мощность силы равна произведению касательной составляющей силы на скорость тела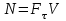


При вращательном движении произведению момента силы относительно оси вращения тела на его угловую скорость.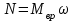


Таким образом, если тело не совершает перемещения, то работа не совершается, однако среди ученых есть мнения другого характера.

Лекция 4

1. 
   Теоремы динамики.
   
2. 
   Меры действия сил
   
3. 
   Теорема об изменении количества движения материальной точки
   
4. 
   Кинетическая энергия точки и системы точек
   

Теоремы динамики
Механическое движение обладает двумя, не противоречащими друг другу, мерами – количеством движения и кинетической энергией.

Если механическое движение передается от тела к телу в форме механического движения, то мерой является количество движения.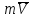



Если же оно передается таким образом, что исчезает, превращается в другие формы движения, то мерой является кинетическая энергия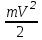
,

как половина произведения массы тела на квадрат его скорости.
Меры действия сил
Мерами действия силы являются импульс силы и работа силы. Наличие этих двух мер обусловлено тем, что силы действуют и во времени и в пространстве, поскольку они возникают в результате взаимодействия материальных тел.

Импульсом силы, измеряют действие силы за некоторый промежуток времени. Различают элементарный импульс силы, и импульс силы за конечный промежуток времени.

Элементарным импульсом силы называется векторная величина, равная произведению вектора силы на элементарный (то есть бесконечно малый) прмежуток времени: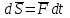
.
Импульсом силы за конечный промежуток времени называется векторная величина, равная интегралу по времени от элементарного импульса силы.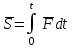

Импульс постоянной силы равен произведению силы на время и направлен по вектору силы, а импульс переменной силы определяют по его проекциям на оси координат: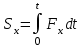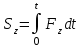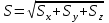




Из этих формул следует, что по ним непосредственно можно вычислить импульсы сил, зависящих от времени или постоянных. Если же сила зависит от расстояния или скорости, то предварительно необходимо найти уравнение движения точки, затем выразить проекции силы на оси координат через время и только после этого по приведенным формулам определить проекции импульса на оси координат.
Теорема об изменении количества движения материальной точки
Настоящая теорема имеет две формы – дифференциальную и интегральную, то есть:

1. 
   Производная по времени от количества движения материальной равна геометрической сумме сил, действующих на точку.
   

2. 
   Изменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов сил, действующих на точку, за тот же промежуток времени.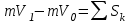
   

где V₁,V₀ – соответственно конечная и начальная скорости объекта движения.
Теорема об изменении кинетической энергии точки состоит в том, что изменение кинетической энергии материальной точки на некотором ее перемещении равно сумме работ всех сил действующих на точку, на том же перемещении.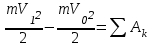

Кинетическая энергия тела при поступательном движении равна половине произведения массы тела на квадрат его скорости.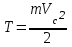


Кинетическая энергия тела при вращательном движении равна половине произведения его момента инерции относительно оси вращения на квадрат его угловой скорости: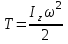

Кинетическая энергия при плоскопараллельном движении равна сумме кинетических энергий поступательного движения тела со скоростью его центра масс и вращательного движения тела вокруг оси, проходящей через центр масс тела.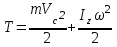

Вращательное движение твердого тела вокруг неподвижной оси описывается уравнением: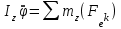

Смысл здесь заключается в том, что произведение момента инерции тела относительно оси вращения на его угловое ускорение равно сумме моментов внешних сил, действующих на тело, относительно оси его вращения.
Кинетическая энергия точки и системы точек
Введение кинетического момента для описания движения механической системы наряду с такой характеристикой, как количество движения, даёт возможность более многогранного изучения механического «поведения» систем. Тем не менее, даже совместное использование этих двух характеристик эффективно далеко не всегда, например, в случае, когда движение механической системы происходит за счёт внутренних сил. Чтобы убедиться в этом, достаточно рассмотреть следующий простой пример. Пусть два одинаковых тела, соединенных пружиной, находятся на гладкой горизонтальной поверхности. Растянем пружину и отпустим грузы, не сообщая им начальной скорости. Под действием внутренних сил они начнут совершать прямолинейные колебания, такие, что скорости тел в каждый момент времени будут равны между собой и противоположно направлены (тела в данном случае перемещаются поступательно). Количество движения системы и ее кинетический момент относительно любой неподвижной точки тождественно равны нулю, хотя система находится в движении; таким образом, в данном случае эти две величины никак не характеризуют движение системы. Поэтому в механике вводится еще одна мера механического движения, называемая кинетической. Кинетической энергией материальной точки называется скалярная величина, равная половине произведения массы точки на квадрат ее скорости.


Лекция 5

1. 
   Понятие о силовом поле.
   
2. 
   Потенциальное силовое поле и силовая функция.
   
3. 
   Работа силы на конечном перемещении в потенциальном силовом поле.
   
4. 
   Поверхности равного уровня и их свойства.
   
5. 
   Потенциальная энергия.
   
6. 
   Закон сохранения механической энергии.
   

Понятие о силовом поле
Силовым полем называется часть пространства, в которой на материальную точку, действует сила поля, зависящая от положения точки в этом пространстве (рисунок 1):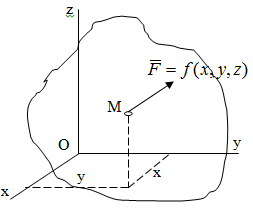

Рисунок 1 – Точка и силовое поле
Таким образом,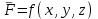
,

или
F_x = f₁(x,y,z),

F_y = f₂(x,y,z),

F_z = f₃(x,y,z).
Силовые поля делятся на стационарные и не стационарные. Стационарным называется такое силовое поле, в котором сила поля не зависит от времени, а не стационарным – такое, в котором сила зависит от времени.


Потенциальное силовое поле и силовая функция
В свою очередь стационарные поля делятся на потенциальные и не потенциальные. Стационарное поле называется потенциальным, если в любой его точке существует некоторая силовая функция U,зависящая от положения точки в поле, частные производные от которой по координатам точки равны проекциям силы поля на координатные оси:
U= f(x,y,z),
(1)
Соответственно, не потенциальное поле, подразумевает неравномерное распределение силовой функции.
Работа силы на конечном перемещении в потенциальном силовом поле
Для уяснения физического значения силовой функции обратимся к известной аналитической формуле элементарной работы силы: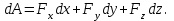

Подставим в это равенство значения проекций силы поля, выраженные через силовую функцию (1) и получим
(2)
Таким образом, мы видим, что смысл силовой функции состоит в том, что ее полный дифференциал есть элементарная работа силы потенциального силового поля (dA = dU).

Стало быть, работу силы потенциального силового поля на некотором конечном перемещении точки ее приложения М₀М можно выразить через силовую функцию U. Обозначим значение силовой функции в начальной точке перемещения (М₀ – U₀), а в конечной точке перемещения (М – U). Тогда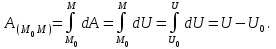


Итак, работа силы потенциального силового поля на некотором перемещении М₀М точки ее приложения равна разности значений силовой функции в конечной и начальной точках этого перемещения: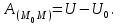

(3)
Особо заметим, что если начальная и конечная точка перемещения совпадают, то работа силы поля на таком перемещении точки ее приложения будет равна нулю: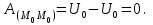

Также из формулы (3) следует также, что работа силы потенциального силового поля не зависит от траектории точки ее приложения, а зависит только от начального и конечного положения этой точки. силы, обладающие такими свойствами называются потенциальными. Примерами таких сил служат сила тяжести и сила упругости.
Поверхности равного уровня и их свойства
Поверхностями равного уровня (или сокращенно поверхностями уровня) называются поверхности, проходящие через точки поля с одинаковыми значениями силовой функции.

Поверхности уровня обладают следующими четырьмя свойствами:

1. 
   Если начальная и конечная точки перемещения точки приложения силы находятся на одной поверхности уровня, то работа силы поля на этом перемещении рана нулю.
   

Действительно, при перемещении точки приложения силы F поля из начального положения М₀ в конечное положение М по любой траектории, которая расположены на одной поверхности уровня U = C (Рисунок 2),

Рисунок 2 – Начальное и конечное перемещение точки М
сила произведет работу

2. 
   Сила потенциального силового поля всегда перпендикулярна к поверхности уровня (Рисунок 3).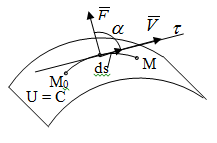
   

Рисунок 3 – Перпендикулярность силового поля и поверхности
Действительно, при перемещении точки приложения силы по поверхности уровня из положения М₀ в положение М работа силы на этом перемещении будет равна нулю (в силу первого свойства поверхностей уровня). Отсюда следует и элементарная работа силы dA на перемещении ds, которое расположено на касательной к поверхности уровня, тоже будет равна нулю, то есть 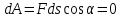. Поскольку F и ds не равны нулю, то нулю будет равен косинус угла альфа. Следовательно угол альфа равен 90⁰, то есть сила F расположена перпендикулярно к поверхности уровня

3. 
   Сила потенциального силового поля всегда направлена в сторону больших значений силовой функции.
   

Пусть свободная материальная точка под действием силы F потенциального силового поля перемещается по направлению силы из положения М₀, расположенного на поверхности уровня со значениями силовой функции U = C₀, в положение М, расположенное на другой поверхности уровня со значениями силовой функции U = C₁ (Рисунок 4).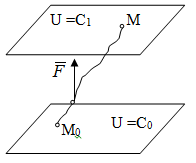


Рисунок 4 – Направление силы потенциального поля
Работа силы поля на этом перемещении будет равна разности значений силовой функции в конечной и начальной точках перемещения (3) и будет положительной:

Следовательно С₁>С₀ и сила действительно направлена в сторону больших значений силовой функции.

4. 
   Сила потенциального силового поля больше там, где поверхности уровня расположены ближе друг к другу.
   

Справедливость этого свойства вытекает из того, что работа силы поля на перемещении точки ее приложения с одной поверхности уровня на другую, соседнюю поверхность уровня, будет одна и та же (так как она равна разности значений силовой функции на этих поверхностях уровней). А посему, там где меньше расстояние между поверхностями уровней, там больше сила (и наоборот, где больше расстояние, там меньше сила). Работа то равна произведению силы на перемещение точки ее приложения, а в данном случае на расстояние между поверхностями уровней.