Учебное пособие для студентов высших учебных заведений очного и заочного обучения
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
|
Теорема об эквивалентных парах на плоскости Данная теорема гласит: две пары, лежащие в одной плоскости и имеющие численно равные моменты и одинаковые направления вращения эквивалентны друг другу. Приведем доказательство теоремы. Пусть в плоскости чертежа действует пара  (Рисунок 8). (Рисунок 8).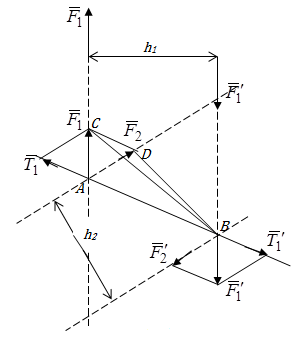 Рисунок 8 - Теорема об эквивалентных парах на плоскости Проведем линии действия этих сил и пересечем их двумя параллельными наклонными прямыми. Проведем через точки А и В пересечения этих наклонных прямых с линиями действия сил  прямую. Перенесем силы прямую. Перенесем силы  по линиям их действия и приложим в точках А и В, а затем разложим их на составляющие, построив соответствующие параллелограммы. по линиям их действия и приложим в точках А и В, а затем разложим их на составляющие, построив соответствующие параллелограммы. В силу разложения одинаковых по модулю сил 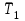 = - = -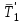 (эти две силы образуют уравновешенную систему сил, так как направлены вдоль одной прямой в разные стороны), (эти две силы образуют уравновешенную систему сил, так как направлены вдоль одной прямой в разные стороны), 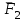 = - = -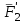 (эти две силы образуют пару сил, так как антипараллельны). Кроме того в силу разложения (эти две силы образуют пару сил, так как антипараллельны). Кроме того в силу разложения 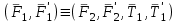 . .Отнимем от полученной в результате разложения системы сил систему сил (  , , ) эквивалентную нулю (на основания аксиомы 2 статики) и тогда будет: ) эквивалентную нулю (на основания аксиомы 2 статики) и тогда будет: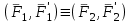 . .Таким образом, имеем, что две пары, лежащие в одной плоскости, имеющие одинаковые направления вращения и численно равные моменты (а моменты этих пар численно равны, так как треугольники АВС и АВD имеют одинаковые площади – у них общее основание и одинаковая высота) эквивалентны друг другу. Свойства пар на плоскости Из рассмотренной теоремы об эквивалентных парах на плоскости вытекают следующие два свойства пар на плоскости: Пару в плоскости ее действия можно как угодно перемещать и поворачивать. У пары можно изменять силы и плечо, сохраняя без изменения момент. Теорема о переносе пары в параллельную плоскость Теорема состоит в том, что действие пары на тело не изменяется от ее переноса в параллельную плоскость. Теорема о сложении пар на плоскости. Она имеет формулировку: система пар на плоскости эквивалентна одной паре, лежащей в той же плоскости, момент которой равен алгебраической сумме моментов всех пар системы ( 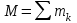 ). ).Докажем теорему на примере сложения трех, расположенных в одной плоскости пар с моментами m1, m2,m3 (Рисунок 9). 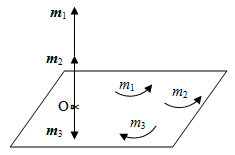 Рисунок 9 – Теорема о сложении пар на плоскости Представим их моменты векторами, приложенными в произвольной точке О плоскости (напомним, что пару в плоскости ее действия можно как угодно перемещать). Получим векторы, расположенные на одной прямой. Их можно сложить и заменить одним вектор-моментом M = m1 + m2 – m3 ,то есть парой с моментом равным алгебраической сумме моментов пар системы расположенной в той же плоскости. Вполне очевидно, что этот результат справедлив для любого числа пар. Теорема о сложении пар в пространстве Эта теорема гласит: система пар в пространстве эквивалентна одной паре, момент которой равен геометрической сумме моментов всех пар системы ( 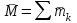 ). ). В самом деле, пусть пары с моментами m1 и m2 лежат в разных плоскостях (Рисунок 10). 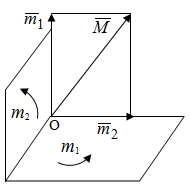 Рисунок 10 – Сложение пар в пространстве Представим их моменты векторами, приложенными в любой точке прямой, образуемой пересечением этих плоскостей. Затем их сложим геометрически и получим вектор-момент 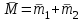 результирующей пары. Действуя подобным образом можно сложить любое число пар в пространстве. результирующей пары. Действуя подобным образом можно сложить любое число пар в пространстве.Условия равновесия пар на плоскости и в пространстве. Для равновесия система пар должна быть эквивалентны нулю, следовательно момент их результирующей пары должен быть равен нулю. Таким образом, учитывая теоремы о сложении пар, имеем: 1. Для равновесия системы пар на плоскости необходимо и достаточно, чтобы алгебраическая сумма моментов всех пар системы была равна нулю: 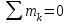 . .2. Для равновесия системы пар в пространстве необходимо и достаточно, чтобы геометрическая сумма моментов всех пар системы была равна нулю: 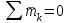 . .Лекция 3 Произвольные системы сил Теорема о параллельном переносе силы. Приведение произвольных систем сил к данному центру. Разные случаи приведения. Условия равновесия произвольных систем сил. Условия равновесия системы параллельных сил. Теорема о параллельном переносе силы Силу, приложенную к твердому телу, можно перенести параллельно самой себе в любую точку тела, если при этом к телу приложить пару, момент которой равен моменту переносимой силы относительно точки переноса (Рисунок 1). 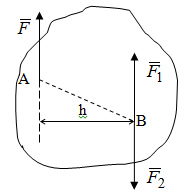 Рисунок 1 - Теорема о параллельном переносе силы Действительно, пусть на твердое тело в точке А действует сила 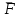 . Действие этой силы на тело не изменится, если в любой его точке В приложим две уравновешенные силы . Действие этой силы на тело не изменится, если в любой его точке В приложим две уравновешенные силы 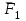 и и 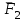 , равные мо модулю силе , равные мо модулю силе 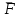 и параллельные ей. Полученная система сил будет представлять из себя силу и параллельные ей. Полученная система сил будет представлять из себя силу 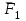 = = 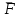 , но приложенную в точке В и пару сил с моментом , но приложенную в точке В и пару сил с моментом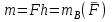 , ,что и требовалось доказать. Приведение произвольных систем сил к данному центру Привести систему сил – это значит максимально ее упростить. Пусть на твердое тело действует произвольная пространственная система сил F1, F2, , Fn. (Рисунок 2). 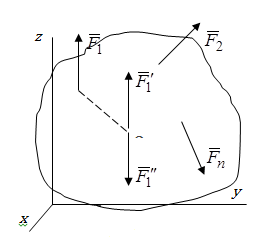 Рисунок 2 – Приведение произвольной системы сил Перенесем, в соответствии с теоремой о параллельном переносе силы, все силы системы в некоторую точку О, именуемую в дальнейшем центр приведения (для примера на рис. 2 показан перенос силы 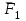 ). В результате получим систему сходящихся в центре приведения сил (пространственную) и систему пар в пространстве. ). В результате получим систему сходящихся в центре приведения сил (пространственную) и систему пар в пространстве.Сходящиеся силы можно сложить и заменить одной силой 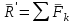 , (1) , (1)именуемой главный вектор системы сил. Систему пар тоже можно заменить одной парой, момент которой равен геометрической сумме моментов всех пар системы:  . (2) . (2)Момент этой пары называется главным моментом системы сил. Таким образом, в общем случае, произвольная пространственная система сил приводится к силе и паре – главному вектору и главному моменту системы. Заметим, что величина главного вектора не зависит от выбора центра приведения, а главного момента – зависит. Главный вектор произвольной системы сил на плоскости определяется также равенством (1), а главный момент равен не геометрической, а алгебраической сумме моментов всех сил системы относительно центра приведения: 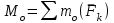 . (3) . (3)Модуль главного вектора системы определяют по той же формуле, что и модуль равнодействующей сходящейся системы сил, а именно: 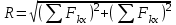 - для произвольной системы сил на плоскости, - для произвольной системы сил на плоскости, - для произвольной системы сил в пространстве. - для произвольной системы сил в пространстве.Направление главного вектора определяют по направляющим косинусам: 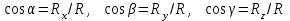 , ,где Rx, Ry, Rz – проекции главного вектора на оси координат, а равны они суммам проекций всех сил системы на эти оси. Главный момент произвольной системы сил на плоскости определяется по формуле (3). Главный момент произвольной пространственной системы сил определяется по его проекциям на координатные оси, поскольку он является вектором (2), по формуле: 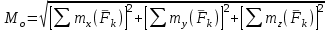 , ,где величины, стоящие в квадратных скобках - есть проекции главного момента системы 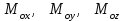 на оси координат x, y, z соответственно. на оси координат x, y, z соответственно.Направление главного момента системы определяется по направляющим косинусам: 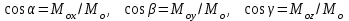 . .Разные случаи приведения произвольной системы сил к данному центру В зависимости от значений главного вектора и главного момента системы возможны следующие четыре частных случая приведения произвольной системы сил к данному центру: 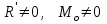 - система приводится к силе и паре, равновесия нет; - система приводится к силе и паре, равновесия нет;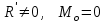 - система приводится к 1 силе (равнодействующей), равновесия нет; - система приводится к 1 силе (равнодействующей), равновесия нет;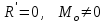 - система приводится к паре, равновесия нет; - система приводится к паре, равновесия нет;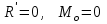 - система эквивалентна нулю и находится в равновесии. - система эквивалентна нулю и находится в равновесии.В первом случае для произвольной системы сил на плоскости возможно дальнейшее упрощение и приведение ее к одной силе, то есть равнодействующей, но она будет проходить не через центр приведения, а смещена параллельно от него на расстояние 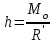 . .Оставим неизменным Мо, но силы пары ( 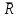 , ,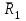 ) возьмем равными по модулю главному вектору ) возьмем равными по модулю главному вектору 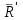 . Тогда плечо пары будет . Тогда плечо пары будет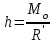 . .После этого пару в ее плоскости переместим и повернем так, чтобы силы 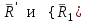 были направлены по одной прямой в разные стороны, то есть давали уравновешенную систему сил, которую отбросим (по аксиоме 2 статики) (Рисунок 3). были направлены по одной прямой в разные стороны, то есть давали уравновешенную систему сил, которую отбросим (по аксиоме 2 статики) (Рисунок 3). Рисунок 3 – Перенос пары в ее плоскости Тогда останется только сила 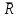 - равнодействующая, линия действия которой смещена от центра приведения О на расстояние - равнодействующая, линия действия которой смещена от центра приведения О на расстояние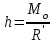 . .Что касается произвольной пространственной системы сил, то в первом случае приведения возможны три различных варианта: Если 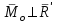 , то такую систему сил можно привести к равнодействующей, не проходящей через центр приведения О. В этом случае главный вектор и пара с моментом , то такую систему сил можно привести к равнодействующей, не проходящей через центр приведения О. В этом случае главный вектор и пара с моментом 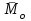 лежат в одной плоскости (Рисунок 4). лежат в одной плоскости (Рисунок 4).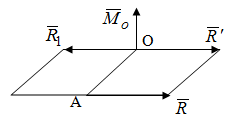 Рисунок 4 – Главный момент расположен перпендикулярно главному вектору Выбрав силы пары 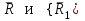 равными по модулю равными по модулю 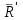 получим, что силы получим, что силы 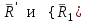 взаимно уравновесятся, и система приведется только к одной силе взаимно уравновесятся, и система приведется только к одной силе 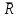 , линия действия которой отстоит от центра приведения О на расстояние ОА = Мо/ , линия действия которой отстоит от центра приведения О на расстояние ОА = Мо/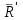 . .Если 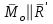 , то система сил приводится к силе и паре, плоскость действия которой перпендикулярна силе (Рисунок 5). , то система сил приводится к силе и паре, плоскость действия которой перпендикулярна силе (Рисунок 5).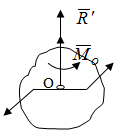 Рисунок 5 – Главный момент расположен параллельно главному вектору Такая совокупность силы и пары называется динамическим винтом или динамой, а линия действия главного вектора называется осью динамы. Дальнейшее упрощение ее невозможно. Если главный вектор и главный момент и не параллельны и не перпендикулярны, то такую систему сил можно привести к динаме, ось которой не будет проходить через центр приведения. Разложим главный момент системы  на составляющие перпендикулярную на составляющие перпендикулярную 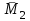 и параллельную и параллельную 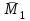 главному вектору главному вектору 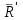 (Рисунок 6). (Рисунок 6).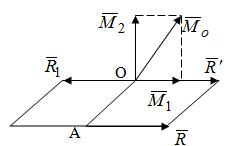 Рисунок 6 - Главный вектор и главный момент и не параллельны и не перпендикулярны 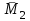 и и 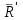 можно привести к силе можно привести к силе 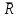 = = 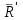 . Тогда останется сила . Тогда останется сила 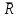 и параллельный ей момент и параллельный ей момент 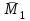 , то есть динама со смещенной осью (ось динамы будет направлена вдоль вектора , то есть динама со смещенной осью (ось динамы будет направлена вдоль вектора 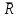 ). ).Условия равновесия произвольных систем сил Условия равновесия произвольной плоской системы сил. Как установлено, данная система сил будет в равновесии только тогда, когда ее главный вектор и главный момент равны нулю. Приравняем к нулю выражения модулей этих величин: 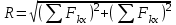 =0, =0,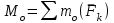 =0. =0.Как видно из этих равенств, это выполнимо при следующих условиях: 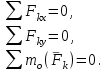 (4) (4)Таким образом, для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил системы на оси х и у, расположенные в той же плоскости, что и силы, были равны нулю и, чтобы сумма моментов всех сил системы относительно любой точки, расположенной в плоскости действия сил, была равна нулю. Эта первая форма условий равновесия называется основной, в ней нет никаких ограничений на выбор положения осей и точки. Кроме основной есть еще две дополнительные формы условий равновесия. Вторая форма условий равновесия: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех сил системы относительно двух точек, лежащих в плоскости действия сил, и сумма проекций всех сил системы на ось, расположенную в той же плоскости и не перпендикулярную отрезку, соединяющему эти точки, были равны нулю.  В этой форме условий равновесия наложены требования на выбор положения оси и точек. Следует иметь ввиду, что если ось х будет перпендикулярна к отрезку АВ, то система может иметь равнодействующую, проходящую через точки А и В и не быть, следовательно, в равновесии, хотя все три уравнения будут выполняться. Предписанный выбор положения оси обеспечивает достаточность этой формы условий равновесия. Третья форма условий равновесия: для равновесия произвольной системы сил на плоскости необходимо и достаточно, чтобы суммы моментов всех сил системы относительно любых трех точек, расположенных в той же плоскости и не лежащих на одной прямой, были равны нулю. Эта форма условий равновесия является достаточной, поскольку, если бы система привелась к равнодействующей, то равнодействующая должна была бы проходить через три точки, не лежащие на одной прямой, а это невозможно. Условия равновесия произвольной пространственной системы сил. Для получения этих аналитических условий приравняем к нулю модули главного вектора и главного момента сил инерции системы.  =0, =0,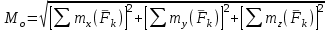 =0. =0.Отсюда видно, что равенство нулю этих величин возможно только при следующих условиях: 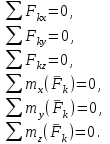 Следовательно, для равновесия произвольной системы сил в пространстве необходимо и достаточно, чтобы суммы проекций всех сил системы на оси x, y, z были равны нулю и, чтобы суммы моментов всех сил системы относительно этих осей были равны нулю. Приведенные условия равновесия справедливы и для систем параллельных сил, так как эти системы сил есть частные случаи произвольных. Однако условия равновесия можно упростить, если одну из осей координат располагать параллельно силам. Тогда условия равновесия будут: Для равновесия системы параллельных сил на плоскости необходимо и достаточно, чтобы сумма проекций всех сил системы на ось параллельную силам и сумма моментов всех сил системы относительно любой точки плоскости, в которой лежат эти силы, были равны нулю Для равновесия системы параллельных сил в пространстве необходимо и достаточно, чтобы сумма проекций всех сил системы на ось параллельную силам и суммы моментов всех сил системы относительно двух других осей были равны нулю. Лекция 4 Сложение двух параллельных и антипараллельных сил. Центр параллельных сил. Центр тяжести твердого тела Координаты центров тяжести однородных твердых тел. Способы определения координат центров тяжести тел. Центры тяжести некоторых однородных тел. Сложение двух параллельных и антипараллельных сил Приведем без доказательства основные положения о сложении этих сил. Равнодействующая двух параллельных сил равна их арифметической сумме и направлена в ту же сторону, что и складываемые силы. Линия действия равнодействующей делит отрезок между точками приложения сил на части обратно пропорциональные силам внутренним образом (рисунок 1). 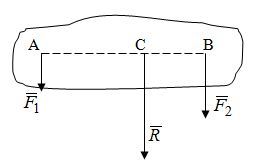 Рисунок 1 – Сложение двух параллельных сил То есть 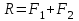 ; ;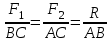 . .Следует иметь ввиду, что положение точки С на отрезке АВ не изменяется ни при каких поворотах тела (или сил  и и  в одну и туже сторону на один и тот же угол). в одну и туже сторону на один и тот же угол).Равнодействующая двух антипараллельных сил равна по модулю разности модулей этих сил, параллельна им и направлена в сторону большей силы. Линия действия равнодействующей делит отрезок между точками приложения сил на части обратно пропорциональные этим силам внешним образом (Рисунок 2). 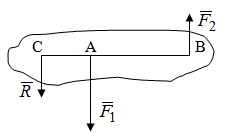 Рисунок 2 – Сложение двух антипараллельных сил То есть 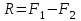 ; ;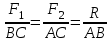 . .Центр параллельных сил Центром параллельных сил называется геометрическая точка С, неизменно связанная с телом, через которую проходит линия действия равнодействующей этой системы параллельных сил при любых их поворотах относительно точек их приложения в одну и ту же сторону на один и тот же угол. Пусть на тело действует система параллельных сил 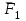 , , 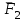 ,…, ,…,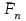 , имеющая равнодействующую , имеющая равнодействующую 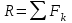 (Рисунок 3). (Рисунок 3).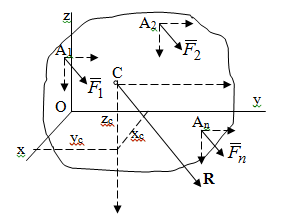 Рисунок 3 – Система параллельных сил и центр параллельных сил Если силы системы поворачивать относительно точек их приложения в одну и ту же сторону, на один и тот же угол, то независимо от этого равнодействующая R будет проходить через неизменно связанную с телом точку С – центр параллельных сил. Определим координаты центра параллельных сил. Расположим силы параллельно оси z и выразим момент равнодействующей относительно осей y и x, а затем расположим силы параллельно оси у и выразим момент равнодействующей относительно оси х, учитывая, что они, согласно теоремы Вариньона, равны сумме моментов всех сил системы относительно этих осей: 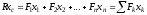 , ,и аналогично 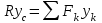 , , 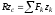 , ,где xk, yk, zk – координаты точек приложения сил. Тогда 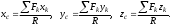 (1) (1)Указанным способом получены формулы координат центра параллельных сил. Центр тяжести твердого тела На каждую k-ю точку тела, находящегося в поле тяжести Земли, действует сила тяжести Рk, направленная к центру Земли. Поскольку размеры любого тела ничтожно малы по сравнению с радиусом Земли, то схождением этих сил можно пренебречь и считать, что они образуют систему параллельных сил. Равнодействующая этих сил 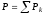 называется силой тяжести тела и она всегда будет проходить через неизменно связанную с телом точку С – центр параллельных сил тяжести всех точек тела, которую и именуют центром тяжести тела. называется силой тяжести тела и она всегда будет проходить через неизменно связанную с телом точку С – центр параллельных сил тяжести всех точек тела, которую и именуют центром тяжести тела.Таким образом, центром тяжести твердого тела называется неизменно связанная с ним геометрическая точка, через которую проходит линия действия силы тяжести тела при любых его положениях в пространстве (поле тяжести Земли). Координаты центра тяжести твердого тела, как центра параллельных сил, определяются формулами (1) и будут: 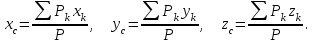 (2) (2)В этом заключается отличие понятий центра тяжести и центра масс. Координаты центров тяжести однородных твердых тел Однородные твердые тела могут быть объемными, плоскими тонкими пластинами, состоять из тонких стержней или проволоки одинакового сечения. Вес всего тела и каждой части таких тел пропорционален объему, площади или длине этой части: Рk = γVk; Рk = γSk; Рk = γlk. Подставим эти значения веса тела и его частей в формулы (2) и сократим γ в числителях и знаменателях. В результате получим формулы координат центра тяжести однородных твердых тел. 1. Для объемного тела 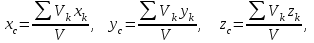 (3) (3)где Vk – объем части тела; V – объем всего тела; xk, yk, zk – координаты части тела. Равенства (3) называют формулами координат центра тяжести объема. 2. Для плоской тонкой пластины  (4) (4)где Sk – площади частей пластины; S– площадь пластины. Выражения (4) называют формулами координат центра тяжести площади. 3. Для тел из тонких однородных стержней или проволоки (или как говорят линии) 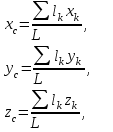 (5) (5)где L – длина всей линии; lk – длины частей линии. Выражения (5) называются формулами координат центра тяжести линии. Таким образом, положения центров тяжести однородных тел определяются как положения центров тяжести соответствующих объемов, площадей, линий. Способы определения координат центров тяжести тел Существуют следующие способы определения координат центров тел: симметрии, разбиения, дополнения, интегрирования и экспериментальные. Рассмотрим каждый из этих способов в отдельности. Способ симметрии. Если однородное тело имеет центр, ось или плоскость симметрии, то центр его тяжести соответственно расположен в центре симметрии, на оси симметрии или в плоскости симметрии. Например, центр тяжести круглого однородного кольца, ромба, прямоугольника, прямоугольного параллелепипеда, шара и прочих тел, имеющих центр симметрии расположен в геометрическом центре симметрии этих тел. 2. Способ разбиения. При этом способе тело разбивается (если это возможно) на несколько частей (объемов, площадей линий), положения центров тяжести которых известно. Затем применяют формулы координат центров тяжести однородных тел, в зависимости от вида тела. Например, пластину можно разбить на два прямоугольника, центры тяжести которых, как известно, находятся в точках пересечения их диагоналей (Рисунок 4). 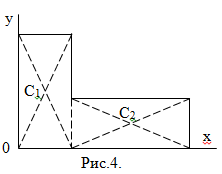 Рисунок 4 – Разбиение прямоугольников Затем применив формулы (4) получим: 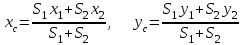 , ,где х1, у1, х2, у2 – координаты точек С1 и С2; S1 и S2 – площади соответствующих прямоугольников. Способ дополнения. Тело, имеющее вырезанную часть, мысленно дополняется этой частью. В результате получают как бы два тела: цельное без выреза и тело, в виде вырезанной части. Далее, если само тело и вырезанную часть можно разбить на части, положения центров тяжести которых известно, применяют способ разбиения. Способ интегрирования. Если тело нельзя разбить на части, положения центров тяжести которых известно, то его разбивают на произвольно малые части, например объемы 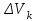 и тогда формулы координат центра тяжести получают вид и тогда формулы координат центра тяжести получают вид 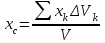 и т. д. Затем переходят к пределу правой части, устремляя и т. д. Затем переходят к пределу правой части, устремляя 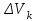 к нулю. Тогда, суммы стоящие в числителях, обращаются в интегралы, распространяющиеся на весь объем тела, и формулы координат центра тяжести получают вид: к нулю. Тогда, суммы стоящие в числителях, обращаются в интегралы, распространяющиеся на весь объем тела, и формулы координат центра тяжести получают вид: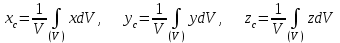 . .Аналогично получают формулы координат центров тяжести площади и линии. Для площади они будут иметь вид: 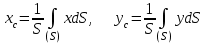 , ,а для линии 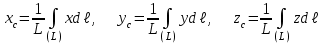 . .Примеры применения способа интегрирования приведены в учебниках. Экспериментальные способы. Эти способы применяют для определения положения центра тяжести неоднородных тел, тел сложной формы, тел составных (машин и их отдельных узлов). Возможны разные способы, например способ подвешивания, способ взвешивания. При первом из упомянутых способов тело подвешивают на нити или тросе за различные его точки. Направление нити, к которой подвешено тело, будет каждый раз давать направление линии действия силы тяжести тела. Точка пересечения этих направлений будет центром тяжести тела. Второй способ, способ взвешивания, покажем на примере определения положения центра тяжести автомобиля (Рисунок 5). 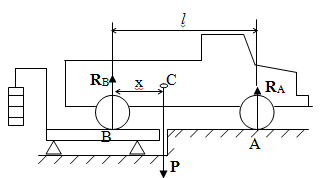 Рисунок 5 – Определение центра тяжести автомобиля Для определения расстояния х замерим расстояние l между осями автомобиля. Определим взвешиванием на весах вес Р автомобиля. Поставим автомобиль задними колесами на платформу весов и определим взвешиванием силу давления их на платформу, а она численно равна реакции RB этих колес. Затем составим уравнение суммы моментов сил, действующих на автомобиль, относительно точки А и приравняем ее к нулю, так как автомобиль находится в равновесии: P(l – x) – RBl = 0. Откуда найдем искомое расстояние: 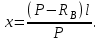 Полученное равенство в конечном случае определяет координату центра тяжести автомобиля. Центры тяжести некоторых однородных тел Центр тяжести площади треугольника расположен в точке пересечения его медиан. Центр тяжести дуги окружности радиуса R лежит на оси ее симметрии на расстоянии от центра О, равном 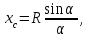 где 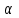 в радианах (Рисунок 6). в радианах (Рисунок 6).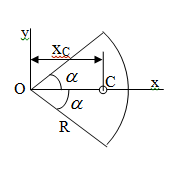 Рисунок 6 – Центр тяжести дуги Центр тяжести площади кругового сектора лежит на оси его симметрии на расстоянии от центра О, равном 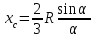 . .Центр тяжести объема пирамиды или кругового конуса лежит на отрезке прямой, соединяющем вершину пирамиды (конуса) с центром тяжести основания, на расстоянии одной четвертой длины этого отрезка от основания пирамиды (конуса). Лекция 5 Трение скольжения. Трение качения. Трение скольжения Трением скольжения называется сопротивление, возникающее при скольжении одного тела по поверхности другого. Представим себе тело. лежащее на некоторой неподвижной горизонтальной поверхности (рис. 1). Если к нему, кроме действующих на него силы тяжести Р и нормальной реакции N, приложим очень малую силу Q (сдвигающую силу) и начнем ее увеличивать, то из опыта известно, что для того , чтобы тело начало скользить по опорной поверхности эта сила должна достичь вполне определенной величины (Рисунок 1). 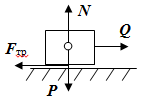 Рисунок 1 – Сила трения скольжения Из этого следует, что со стороны опорной поверхности на тело кроме нормальной реакции действует сила, препятствующая скольжению тела. Эту силу называют силой трения скольжения. Ее будем обозначать Fтр. О величине трения скольжения судят по этой силе. Итак, с увеличением сдвигающей силы, растет и сила трения скольжения и уравновешивает сдвигающую силу до тех пор, пока тело не начнет двигаться (скользить) по опорной поверхности. Момент, предшествующий началу скольжения тела, называется порогом покоя. До порога покоя силу трения называют силой трения скольжения в покое. При пороге покоя сила трения скольжения в покое достигает максимальной величины. После порога покоя силу трения называют силой трения скольжения в движении. Она может изменяться по разному - увеличиваться или уменьшаться по сравнению с максимальной силой трения скольжения в покое, но она всегда будет меньше сдвигающей силы. Характер взаимосвязи сил Q и Fтр представлен на рисунке 2. 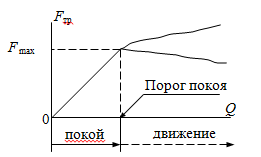 Рисунок 2 – Порог покоя Следует заметить, что зависимости, о которых идет речь в данной лекции относятся к сухому трению, то есть тому, когда трущиеся поверхности не разделены каким-либо третьим телом (смазкой, водой, окисными пленками и т д.). Путем многочисленных опытов Кулон установил, что максимальная сила трения скольжения (в покое) равна произведению коэффициента трения скольжения в покое f на нормальное давление тела на опорную поверхность или, что количественно то же, на нормальную реакцию N опорной поверхности Fmax= fN . Сила трения скольжения в движении тоже пропорциональна нормальному давлению трущихся тел друг на друга: 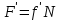 , ,где 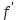 - коэффициент трения скольжения в движении, который несколько меньше коэффициента трения скольжения в покое и, как правило, с увеличением скорости уменьшается до некоторой постоянной величины. - коэффициент трения скольжения в движении, который несколько меньше коэффициента трения скольжения в покое и, как правило, с увеличением скорости уменьшается до некоторой постоянной величины.Из приведенных зависимостей следует, что коэффициент трения скольжения является величиной безразмерной. Значения коэффициентов трения скольжения определяется опытным путем и зависит от многих факторов: материалов трущихся тел, шероховатости соприкасающихся поверхностей, влажности, температуры, направления скольжения – вдоль или поперек волокон (для волокнистых тел), от скорости скольжения и других. Следует также иметь ввиду, что приведенные зависимости являются приближенными и далеко не полно отражают сложности процессов трения, но дают в ряде случаев достаточную точность и поэтому широко применяются. Что касается причин возникновения трения скольжения, то в основном они состоят в геометрическом сцеплении шероховатостей соприкасающихся поверхностей и их молекулярном взаимодействии. Полезно или нет трение – сказать однозначно невозможно. Если бы не было трения, то мы не смогли бы ходить (достаточно вспомнить, как скользят ноги на льду), машины передвигаться; гвозди бы, шурупы, болты не могли скрепить детали (они тоже держатся трением). Не было бы тканей, так как нити в них держатся силами трения. Подобные примеры бесконечны. Так. Что трение отнюдь не вредное явление. Оно вредно в машинах, так как поглощает энергию на бесполезную работу, вызывает износ деталей, снижает надежность и эффективность машин, поэтому с ним борются. Многие задачи на равновесие тел на поверхности с трением удобно решать геометрически, используя понятия угол трения и конус трения. Угол трения. На тело, находящееся на поверхности с трением, при приложении сдвигающей силы Q со стороны этой поверхности действуют сила трения скольжения в покое Fтр и нормальная реакция реакция N, которые имеют равнодействующую R. При пороге покоя эта равнодействующая R образует с нормалью угол 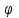 , который называется углом трения (рисунок 3). , который называется углом трения (рисунок 3).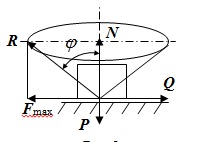 Рисунок 3 – Угол трения Угол трения интересен тем, что его тангенс, как следует из рис. 3, равен коэффициенту f трения скольжения в покое: 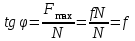 . .Конус трения. При доведении тела до порога покоя по всем направлениям его скольжения по опорной поверхности полная реакция R поверхности опишет конус, который называется конусом трения (Рисунок 4). 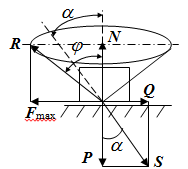 Рисунок 4 – Конус трения Конус трения интересен тем, что пока сила, действующая на тело, находится внутри конуса трения или на его образующей тело будет в покое. В самом деле, пусть на тело действует сила S, образующая с нормалью угол 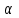 . Разложим ее на силы Р и Q. Тело будет в покое при условии . Разложим ее на силы Р и Q. Тело будет в покое при условии 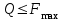 . .Q = Ptgα, или, учитывая, что P = N, Q = Ptgα =Ntgα. Тогда, учитывая, что 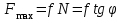 условие равновесия тела будет: 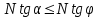 . .Отсюда следует, что пока 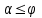 тело будет находится в покое, какой большой не была бы сила S. тело будет находится в покое, какой большой не была бы сила S.Заметим, что конус и угол трения используются при экспериментальном определении коэффициента трения скольжения в покое с помощью наклонной плоскости. Тело помещают на наклонную плоскость и медленно увеличивают угол наклона, доводя его до порога покоя, то есть начала скольжения. В этот момент линия действия силы тяжести будет проходить по образующей конуса трения, а угол наклона плоскости будет равен углу трения, а 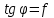 . .Коснемся, для расширения кругозора, теоремы Эйлера о трении нити о цилиндрическую поверхность: 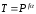 , ,где Т – сдвигающая сила; Р – удерживающая сила; f– коэффициент трения скольжения нити о поверхность; 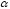 - угол охвата нитью цилиндрической поверхности (Рисунок 5). - угол охвата нитью цилиндрической поверхности (Рисунок 5).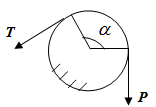 Рисунок 5 – Трение нити о цилиндрическую поверхность Трение нити о цилиндрическую поверхность весьма велико. Так, если канат обмотать вокруг цилиндра 3 раза ( 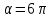 ), то при f =0,35 силой Р = 15 Н можно уравновесить силу Т = 10000 Н. ), то при f =0,35 силой Р = 15 Н можно уравновесить силу Т = 10000 Н.И еще один интересный факт, что при передвижении тела скольжением, например тянуть его веревкой, наименьшее усилие будет в том случае, когда угол наклона веревки к поверхности будет равен углу трения тела о поверхность. Трение качения Трением качения называется сопротивление, возникающее при перекатывании одного тела по другому. Так, если к катку приложить сдвигающую силу Q, то возникнет равная ей модулю и противоположная по направлению сила трения скольжения Fтр . (Рисунок 6) 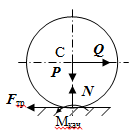 Рисунок 6 – Каток и сдвигающая сила при трении качения Эта пара сил будет стремиться катить каток, однако он начнет катиться лишь тогда, когда момент ее достигнет определенной величины. Следовательно, со стороны опорной поверхности действует пара сил, препятствующая качению катка. Трение качения оценивается моментом этой пары – пары терния качения. Максимальный момент ее будет при пороге покоя. Он, как установил Кулон, пропорционален нормальному давлению соприкасающихся тел: Mкач = fkN, где fk - коэффициент трения качения (плечо пары трения качения). Коэффициент трения качения зависит от упругих свойств материала катка и опорной поверхности, для сильно деформируемых тел зависит еще и от радиуса катка. Определяют его опытным путем, и равен он тысячным долям метра. Возникновение пары трения качения объясняется тем, что в силу деформации и катка, и опорной поверхности они соприкасаются не по образующей катка, а на некоторой площадке. Образно выражаясь, каток продавливает лунку в опорной поверхности (Рисунок 7). 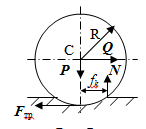 Рисунок 5 – Пара трения качения При отсутствии силы Qнормальная реакция N поверхности проходит через центр тяжести катка, по линии действия силы тяжести и численной равна ей. После приложения и постепенного увеличения, до порога покоя тела, силы Q нормальная реакция смещается в направлении силы Q на край лунки и силы Р и N образуют пару трения качения – оказывающую сопротивление качению. В момент начала качения каток, как рычаг, поворачивается относительно точки приложения силы N, снова проминая опорную поверхность, и этот процесс продолжается во все время движения катка. Что касается покоя катка, то он будет в покое при 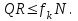 Теперь сопоставим силы необходимые для скольжения и качения катка: для скольжения катка необходима сила Qск = fN. для качения катка необходима сила 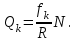 Поскольку 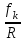 << f , << f ,то Qk << Qск. Таким образом сила необходимая для качения тела во много раз (практически в десятки раз) меньше силы необходимой для перемещения тела скольжением. Поэтому в технике, где это только возможно, вместо подшипников скольжения применяются подшипники качения (шариковые, роликовые, игольчатые). Между прочим, следует отметить, что первый в мире прообраз шарикового подшипника был сделан и применен в России. История эта такова. Во времена Екатерины Второй для изготовления пьедестала памятнику Петру 1 «Медный всадник» скульптору Фальконе в 1678 году потребовалась большая скала гранита. Нашли ее в 20 км от места установки памятника, на другом берегу Невы, в Финляндии. Размеры ее были 16×8×7 м3, а вес 2500 т. Сначала сделали модель скалы в 1/10 натуральной величины и попробовали передвигать ее на катках, но опыт и расчеты показали, что имеющегося тягла (людей и лошадей) для перемещения скалы недостаточно. Затем из березы выточили шары, которые поместили в желоба, окованные железом. Поверх шаров положили деревянную платформу, а на нее скалу и с помощью такого устройства передвинули скалу до Невы, там ее закатили на притопленную баржу, переправили на другой берег, и снова, по суше, докатили до места установки памятника, поворачивая на перекрестках на шарах в круговых желобах. Вся работа была завершена с марта по сентябрь 1769 года. Контрольные вопросы к разделу «Статика» 1. Что называется теоретической механикой? 2. Что понимается под механическим движением? 3. Давно ли возникла теоретическая механика? 4. Какими методами пользуется теоретическая механика? 5. На какие разделы делится теоретическая механика? 6. Что называется статикой? 7. Что понимается под равновесием твердого тела? 8. Что понимается под твердым телом в теоретической механике? 9. Какое воздействие (взаимодействие) тел называется механическим? 10. Что называется силой? 11. Какими факторами определяется действие силы на твердое тело? 12. Какое тело называется свободным? 13. Какие тела называются несвободными? 14. Что называется связями? 15. Что называется реакциями связей? 16. Что значит “сложить сходящиеся силы”? 17. Какие способы сложения сходящихся сил существуют? 18. В чем заключается геометрический способ сложения сходящихся сил? 19. Как производится сложение сходящихся сил аналитическим способом? 20. Чему равна равнодействующая системы сходящихся сил при равновесии? 21. Какое действие силы оценивает ее момент? 22. Какие моменты силы относительно точки различают? 23. Что называется алгебраическим моментом силы относительно точки? 24. Какими факторами характеризуется действие момента силы относительно точки? 25. Как момент силы относительно точки изображают вектором? 26. В чем состоит теорема о параллельном переносе силы? 27. Что значит “привести” произвольную систему сил к данному центру? 28. Как осуществляется приведение произвольной системы сил к данному центру и каков его результат? 29. Чему равны модули главного вектора R| и главного момента Мо произвольной системы сил на плоскости? 30. Чему равны модули главного вектора R| и главного момента Мо произвольной пространственной системы сил? |
