Учебное пособие для студентов высших учебных заведений очного и заочного обучения
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
|
Раздел III. Динамика Лекция 1 Введение в динамику. Законы динамики материальной точки. Дифференциальные уравнения движения точки. Две основные задачи динамики точки и порядок их решения. Относительное движение точки, принцип относительности классической механики, относительное равновесие. Введение в динамику Динамикой называется раздел теоретической механики, в котором изучается движение материальных твердых тел с учетом их инерции (инертности) и действующих на них сил. Под инерцией понимается свойство материальных тел сопротивляться изменению их покоя или равномерного прямолинейного поступательного движения. Мера инерции – это скалярная величина, именуемая массой. Она характеризует, как инерционные, так и гравитационные свойства вещества. При вращательном движении твердого тела мерой его инерции является момент инерции относительно оси вращения. В динамике, в отличие от статики, учитывается действие всех сил, как постоянных, так и переменных. Переменные силы могут зависеть от расстояния, от скорости, от времени. Например, отскок металлического шарика от бетонного пола будет тем выше, чем выше мы поднимем его от поверхности пола – соответственно просматривается зависимость от расстояния, от скорости могут зависеть силы сопротивления движению, от времени – сила тяги двигателя при изменении подачи топливо-воздушной смеси. Твердые тела в динамике представляют двумя моделями: материальной точкой или механической системой. Под материальной точкой понимается точка, обладающая массой данного тела. Она является простейшей моделью твердого тела, поскольку в данном случае размерами, габаритами, формой тела пренебрегают, что облегчает изучение движения тела под действием сил. Здесь необходимо отметить, что, принимая тело за точку, изучают движение не абстрактной точки, а центра масс или центра тяжести тела. За материальные точки можно принимать тела, размеры которых малы по сравнению с проходимыми ими расстояниями (например, перемещение автобусов, поездов и другого транспорта на далекие расстояния или пуля, выпущенная из ружья, вес размер которой действительно очень мал в сравнении с дальностью полета). Под механической системой понимается совокупность взаимосвязанных материальных точек, в которой положение и движение каждой точки, сказывается на положении и движении других точек. Эта модель может быть использована тогда, когда тело (механизм, конструкцию и т.д.) нельзя представить в виде точки. Законы динамики материальной точки В основе динамики лежат три закона Ньютона – закон инерции, второй (основной) закон динамики точки, закон равенства действия и противодействия. Эти законы впервые, в систематизированном виде, были изложены в книге «Математические начала натуральной философии», написанной Исааком Ньютоном и опубликованной еще в 1687 году. Первый закон – закон инерции состоит в том, что изолированная от внешних воздействий материальная точка будет находиться в состоянии покоя или равномерного прямолинейного движения. Он устанавливает эквивалентность состояния покоя и равномерного прямолинейного движения. Позволяет судить о том, находится ли точка под действием неуравновешенной силы. Второй (основной) закон динамики точки, гласит, что произведение массы точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе и направление ускорения совпадает с направлением силы: mW = F В случае же действия на тело нескольких сил, системы сил, то в правой части равенства будет находиться геометрическая сумма сил. 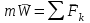 Этот закон является единственным из трех законов Ньютона, имеющим количественное выражение (почему и называется основным) и он справедлив только для точек постоянной массы. Например, в 2019 году в Японии планируется выпуск мотоциклов, оснащенных гироскопом, то есть устройством, которое помогает водителю удерживать равновесие мотоцикла за счет центробежных сил специально выполненного вращающегося диска. Третий закон – закон равенства действия и противодействия, состоит в том, что при всяком действии одной материальной точки на другую имеет место такое же по величине, но противоположное по направлению взаимодействие. Этот закон также имеет большое значение при решении технических, производственных, экспериментальных и других задач. Для уточнения, все законы Ньютона справедливы для движения тел в инерциальной системе отсчета. Инерциальной называется такая система отсчета, в которой выполняется закон инерции. Она считается неподвижной и в технической практике за систему такого типа принимается система отсчета жестко связанная с Землей, предметами или телами, расположенными на поверхности Земли. Поскольку тела в динамике могут представляться материальной точкой и механической системой, то динамика делится на динамику точки и динамику системы. Дифференциальные уравнения движения точки Согласно второго (основного) закона динамики точки: 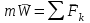 (1) (1)Спроектируем обе части этого векторного равенства на оси декартовой системы координат и получим следующие три зависимости: 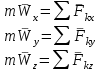 Из раздела кинематики известно, что проекции ускорения очки на оси координат равны вторым производным по времени от соответствующих координат точки. С учетом этого уравнения получат вид:  Полученные таким образом уравнения и являются дифференциальными уравнениями движения точки в декартовой системе координат. Если обе части уравнения (1) спроектируем на естественные оси координат (касательную и нормальную), то получим дифференциальные уравнения движения точки относительно этих осей. 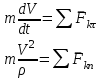 Две основные задачи динамики точки С помощью дифференциальных уравнений движения решаются две основные задачи динамики точки. Первая основная задача состоит в том, что по известной массе точки и уравнениям ее движения (x(t), y(t), z(t)) необходимо определить действующую на точку силу. Решение задачи проводят в следующем порядке: Определяют проекции ускорения на оси координат. Они равны вторым производным по времени от соответствующих координат точки: 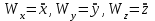 Массу точки умножают на эти проекции ускорения и находят проекции силы Rx, Ry, Rz на оси координат: Определяют модуль силы по формуле: 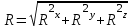 Определяют направление силы по направляющим косинусам: cosα= Rx/R, cosβ= Ry/R, cosφ= Rz/R Вторая основная задача состоит в том, что по известной массе точки и действующим на нее силам необходимо определить движение точки. Решение задачи проводят в следующей последовательности: Необходимо выполнить рисунок, на котором поместить точку в систему координат в произвольном положении на предполагаемой или указанной в задаче траектории, таким образом, чтобы все координаты точки были положительными. Показать все действующие на точку силы. Составить дифференциальные уравнения движения точки относительно каждой координатной оси. Решить эти уравнения и найти уравнения движения точки (x(t), y(t), z(t)). Постоянные интегрирования при решении дифференциальных уравнений определяют по начальным условиям. К начальным условиям относятся: начальное время t0, проекции начальной скорости на оси координат V0x, V0y, V0z, начальные координаты x0, y0, z0. Динамика относительного движения точки Движение точки в инерциальной (условно неподвижной системе отсчета) изучают с помощью основного уравнения динамики точки: 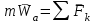 (1) (1)Необходимо отметить, что в этом уравнении Wa – это абсолютное ускорение точки. Поэтому становится непонятным, имеется ли возможность использования методов, основанных на этом законе применять при изучении движения точки в подвижной системе отсчета. Для решения поставленной проблемы найдем зависимость между относительным ускорением точки и силами. Абсолютное ускорение точки, согласно теоремы Кориолиса равно геометрической сумме ее переносного, относительного и кориолисова ускорений: 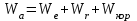 С учетом этого, выражение (1) примет вид: 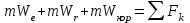 . .Далее выразим  (3) (3)Величины, стоящие в круглых скобках, представляют собой силы и называются переносной силой инерции и кориолисовой силой инерции. Обозначим их и равенство примет вид: 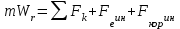 Это уравнение показывает зависимость между относительным ускорением точки и силами. Оно называется основным законом динамики относительного движения точки. Приходим к выводу, что основное уравнение динамики для относительного движения точки составляется также, как и основное уравнение динамики для движения точки в инерциальной системе отсчета, только к действующим силам необходимо добавить переносную и кориолисову силы инерции точки. В случае, когда переносное движение будет равномерным и прямолинейным: 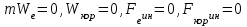 Тогда уравнение (3) получит вид: 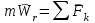 . .То есть такой же вид что и уравнение (1). Из этого вытекает принцип относительности классической механики: находясь в изолированной системе никаким механическим опытом невозможно проверить находится ли эта система в покое или движется равномерно и прямолинейно. Под относительным равновесием точки понимается состояние покоя точки в относительном движении. При нем относительная скорость и относительное ускорение точки равны нулю. Также равно нулю кориолисово ускорение, а значит и кориолисова сила инерции. Отсюда следует условие относительного равновесия точки: для относительного равновесия точки необходимо и достаточно, чтобы геометрическая сумма сил, действующих на точку со стороны других тел, и переносной силы инерции точки была равна нулю. Иными словами 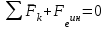 что и требовалось доказать. Лекция 2 Дифференциальные уравнения движения механической системы. Центр масс механической системы. Теорема о движении центра масс механической системы. Сохранение движения центра масс. Дифференциальные уравнения движения механической системы Рассмотрим механическую систему, состоящую из n точек. Положение k-й точки определяется радиус-вектором rk . Точка имеет массу mk и движется со скоростью Vk и с ускорением 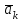 . .Силы, действующие на материальную точку можно разбить на две группы. Сделать это можно разными способами: Разделим силы, действующие на k-ю точку, на внешние и внутренние. Получим следующую запись основного уравнения динамики: 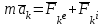 , k = 1,2,…,n. (1) , k = 1,2,…,n. (1)где Fke – «external» равнодействующая внешних сил; Fki – «internal» равнодействующая сил, действующих со стороны тел системы. Разделим силы, действующие на k-ю точку, на активные силы и реакции связей. Получим следующую запись: 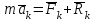 , k = 1,2,…,n. (2) , k = 1,2,…,n. (2)где Fk – равнодействующая активных сил, приложенных к точке k; Rk – равнодействующая реакций связей, действующих на точку k. При этом выполняется равенство: 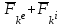 = =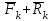 Первый способ записи основного уравнения используется при решении задач динамики с помощью основных теорем динамики, которые включают в себя: 1. Теорему о движении центра масс. 2. Теорему об изменении количества движения. 3. Теорему об изменении кинетического момента. 4. Теорему об изменении кинетической энергии. Второй способ записи основного уравнения применяется при решении задач динамики методами аналитической механики, которые используют: 1.Принцип Лагранжа. 2.Принцип д’Аламбера. 3.Принцип д’Аламбера – Лагранжа. 4.Уравнения Лагранжа второго рода. Центр масс механической системы Массой механической системы называется сумма масс ее точек:  (3) (3)Центром масс механической системы называется геометрическая точка С, радиус-вектор которой определяется по формуле: 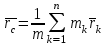 (4) (4)Проектируя последнее равенство на оси, получим формулы для координат центра масс, которые аналогичны формулам для определения координат центра тяжести: 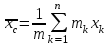 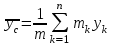 (5) (5)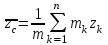 Центр масс иногда называют центром инерции. Центр масс более общее понятие, чем центр тяжести, поскольку сохраняет смысл даже при отсутствии сил тяжести. Если массы материальных точек постоянны, то дифференцированием уравнения (4) получим выражение для скорости центра масс: 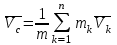 , (6) , (6)а также выражение 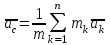 , (7) , (7)для определения ускорения центра масс системы. Теорема о движении центра масс механической системы Произведение массы системы на ускорение центра масс равно главному вектору внешних сил, действующих на точки системы: 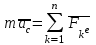 (8) (8)или в проекциях на оси 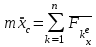 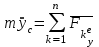 (9) (9)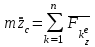 Просуммируем все дифференциальные уравнения движения механической системы (1), в результате чего получим. 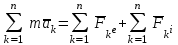 (10) (10)Если учесть, что силы взаимодействия внутри системы попарно равны и противоположно направлены, получим, что главный вектор внутренних сил равен нулю:  Кроме этого, по формуле (3.7) имеем: 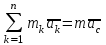 Отсюда следует справедливость уравнений (3.8), которые называются дифференциальными уравнениями поступательного движения твердого тела, что и требовалось доказать. Другими словами, центр масс механической системы движется как материальная точка, в которой сосредоточена вся масса системы и к которой приложены все внешние силы, действующие на систему, внутренние силы не могут изменить движение центра масс. Сохранение движения центра масс Следствие 1 Если главный вектор внешних сил механической системы все время равен нулю, то центр масс системы находится в покое или движется равномерно и прямолинейно. Действительно, если 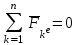 , ,то из формулы (8), получаем, что  Следствие 2 Если сумма проекций всех внешних сил на какую-либо ось все время равна нулю, то проекция скорости центра масс на эту ось постоянна. Действительно, если 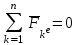 , ,то из формулы (9), получаем что 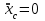 Отсюда следует, что xc = const, Vcx = const, а центр масс движется по оси x равномерно или покоится. |
