Учебное пособие для студентов высших учебных заведений очного и заочного обучения
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
|
Раздел II. Кинематика Лекция 1 Предмет кинематики и ее основные понятия и определения. Кинематика точки. Способы задания движения точки Связь способов задания движения точки между собой Скорость точки при векторном способе задания ее движения Ускорение точки при векторном способе задания ее движения Скорость точки при координатном способе задания ее движения Ускорение точки при координатном способе задания ее движения Скорость точки при естественном способе задания ее движения Ускорение точки при естественном способе задания ее движения Частные случаи движения точки. Предмет кинематики и ее основные понятия и определения Кинематикой называется раздел теоретической механики, в котором изучается механическое движение твердых тел с геометрической стороны, то есть без учета их инерции и действующих сил. Под механическим движением понимается изменение положения тела в пространстве с течением времени относительно других тел, называемых телами отсчета. Телом отсчета называется тело, по отношению к которому определяется положение данного тела. Совокупность тела отсчета и жестко связанной с ним системы координат называется системой отсчета. На рисунках тело отсчета обычно не изображается, а изображаются только координатные оси. Пространство в классической механике трактуется как трехмерное евклидовое с одинаковыми свойствами во всех точках и направлениях, не зависящими от находящихся в нем тел и их движений. Время предполагается одинаковым во всех системах отсчета, не зависящим от относительного движения этих систем. Оно является скалярной, непрерывно изменяющейся величиной, играющей в задачах кинематики роль независимой переменной величины. Такие пространство и время отражают реальные их свойства приближенно. Однако для движений со скоростями, далекими от скорости света, это допущение дает вполне достаточную для практики точность. Следует иметь ввиду, что если система отсчета не указана, то изучение механического движения тела невозможно. Механическое движение обладает относительностью, поскольку по отношению к разным телам отсчета оно различно (в силу их разного перемещения – в природе неподвижных тел нет). Так, например, поршень дизеля, движущегося прямолинейно и равномерно трактора, относительно блока цилиндров совершает возвратно-поступательное прямолинейное движение, а по отношению к поверхности Земли он перемещается по синусоиде. Относительность механического движения проявляется и в том, что при наличии в пространстве только двух тел, наблюдателю, находящемуся на одном из низ, невозможно установить какое из этих тел находится в покое, а какое движется. Вспомните, когда вы смотрите из вагона стоящего поезда только на вагон другого поезда, стоящего на соседнем пути, то вы не можете установить, пока не посмотрите на перрон, какой из поездов начал движение. Относительность движения хорошо описана в стихотворениях А.С. Пушкина и М.В. Ломоносова. Так, у А.С. Пушкина: Движенья нет, сказал мудрец брадатый. Другой смолчал и стал пред ним ходить. Сильнее бы не смог он возразить; Хвалили все ответ замысловатый. Но, господа, забавный случай сей Другой пример на память мне приводит: Ведь каждый день пред нами Солнце ходит, Однако ж прав упрямый Галилей. У М.В. Ломоносова: Случились вместе два астронома в пиру И спорили весьма между собой в жару. Один твердил:”Земля, вертясь, круг Солнца ходит”; Другой, что Солнце все с собой планеты водит. Один Коперник был, другой слыл Птоломей. Тут повар спор решил усмешкою своей. Хозяин спрашивал:”Ты звезд теченье знаешь? Скажи, как ты о сем сомненье рассуждаешь?”. Он дал ответ:”Что в том Коперник прав, Я правду докажу на Солнце не бывав. Кто видел простака из поваров такова, Который бы вертел очаг кругом жаркова?”. В кинематике твердые тела представляются двумя моделями: точкой и абсолютно твердым телом. При моделировании тела точкой его формой и размерами пренебрегают. Наличие этих моделей обуславливает деление кинематики на кинематику точки и кинематику твердого тела. Задачами кинематики точки являются: задание движения точки относительно данной системы отсчета; определение кинематических характеристик движения точки (траектории, скорости, ускорения). В кинематике твердого тела решаются следующие задачи: задание его движения относительно данной системы отсчета; определение общих для всех точек тела кинематических характеристик; определение кинематических характеристик отдельных точек тела. Задать движение точки или твердого тела – это значит указать способ, позволяющий определить их положение в пространстве относительно данной системы отсчета в любой момент времени. Если движение не задано, то изучать его невозможно. Траекторией точки называется линия, описываемая точкой при ее движении. Скоростью точки называется вектор 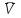 , характеризующий в каждый момент времени быстроту и направление движения точки. , характеризующий в каждый момент времени быстроту и направление движения точки.Ускорением точки называется вектор 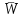 , характеризующий быстроту изменения ее скорости, как по модулю, так и по направлению. , характеризующий быстроту изменения ее скорости, как по модулю, так и по направлению.Кинематика точки. Способы задания движения точки Движение точки может задаваться тремя способами: координатным, естественным и векторным. Координатный способ состоит в том, что положение точки в данной системе отсчета в каждый момент времени определяется ее координатами, непрерывно изменяющимися с течением времени: 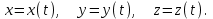 Эти уравнения называются уравнениями (законом) движения точки в декартовой системе координат. Одновременно эти уравнения являются уравнениями траектории точки в параметрической форме. Для получения уравнения траектории точки в обычной форме из них надо исключить параметр t (время) и связать координаты точки между собой непосредственно. Например, если х = 2t, y = 12t2, то уравнение траектории точки будет y = 3х2. Движение точки можно задать, пользуясь и другими системами координат, например, полярными, сферическими и т. д. Естественный способ заключается в том, что траекторию точки, заранее известную или заданную, рассматривают как координатную ось (Рисунок 1). 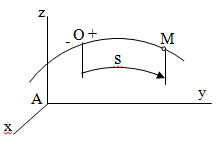 Рисунок 1 – Естественный способ задания движения точки На ней выбирают начало отсчета, указывают положительное и отрицательное направления отсчета и уравнение (закон) движения точки вдоль траектории в виде 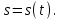 Это равенство называется уравнением (законом) движения точки в естественной форме. Необходимо иметь ввиду, что s есть не путь, пройденный точкой за данное время, а расстояние от начала отсчета до точки в данный момент времени, измеренное вдоль траектории или, как говорят, криволинейная координата точки. Векторный способ состоит в том, что положение точки в данной системе отсчета определяется ее радиус-векторм 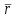 , проведенным к точке из начала координат (точка всегда находится на конце этого вектора) и, являющимся функцией времени: , проведенным к точке из начала координат (точка всегда находится на конце этого вектора) и, являющимся функцией времени: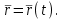 Это равенство называется уравнением (законом) движения точки в векторной форме (Рисунок 2). 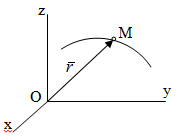 Рисунок 2 – Задание движения точки через годографа радиус-вектора Отметим, что геометрическое место концов радиус-вектора 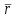 (годограф радиус-вектора (годограф радиус-вектора 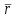 ) будет траекторией точки. ) будет траекторией точки.Связь способов задания движения точки между собой Векторный и координатный способы задания движения точки связаны между собой зависимостью 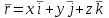 , ,а естественный способ с координатным зависимостью вида 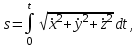 где – под корнем стоят производные по времени от координат точки. Скорость точки при векторном способе задания ее движения Пусть в момент времени t точка занимала положение М, определяемое радиус-вектором 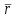 , а в момент времени t1 положение М1, определяемое радиус-вектором , а в момент времени t1 положение М1, определяемое радиус-вектором 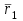 (Рисунок 3). (Рисунок 3).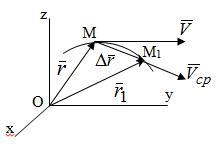 Рисунок 3 - Скорость точки при векторном способе задания ее движения Таким образом, за время 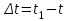 радиус-вектор точки получил приращение радиус-вектор точки получил приращение 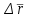 = = 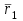 - -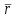 , которое называют вектором перемещения. , которое называют вектором перемещения.Отношение вектора перемещения к промежутку времени  дает векторную величину, называемую средней скоростью точки за этот промежуток времени: дает векторную величину, называемую средней скоростью точки за этот промежуток времени: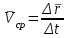 . .Направлена средняя скорость точки вдоль вектора перемещения в сторону движения точки. В задачах кинематики средней скоростью пользуются редко, как правило в расчетах используют скорость точки в данный момент времени (данное мгновение). Для определения скорости точки в данный момент времени надо определить предел средней скорости при стремлении  к нулю: к нулю: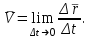 А этот предел, учитывая, что радиус-вектор есть функция времени, дает первую производную по времени от радиус-вектора точки. Следовательно, вектор скорости точки в данный момент времени равен первой производной по времени от ее радиус-вектора: 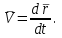 Направлен вектор скорости точки по касательной к ее траектории в сторону ее движения. Ускорение точки при векторном способе задания ее движения Предположим, что в момент времени t точка была в положении М и имела скорость 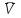 , а по прошествии некоторого времени , а по прошествии некоторого времени  переместилась в положение М1 и скорость ее стала переместилась в положение М1 и скорость ее стала 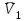 (Рисунок 4). (Рисунок 4).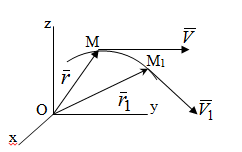 Рисунок 4 - Ускорение точки при векторном способе задания ее движения Таким образом, за время  скорость точки изменилась на величину скорость точки изменилась на величину 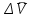 (рисунок 5). (рисунок 5).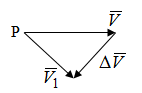 Рисунок 5 – Быстрота изменения скорости Если это приращение скорости разделим на указанное приращение времени, то получим величину, именуемую средним ускорением точки за время  : :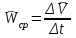 . .Для определения ускорения точки в данный момент времени возьмем предел среднего ускорения, устремив  к нулю и получим: к нулю и получим: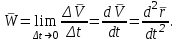 Следовательно, вектор ускорения точки равен первой производной по времени от вектора скорости точки или второй производной по времени от ее радиус-вектора. Полученные выражения скорости и ускорения точки служат исходными для определения скорости и ускорения точки при других способах задания ее движения. Скорость точки при координатном способе задания ее движения Пусть движение точки задано уравнениями: x = x(t), y = y(t), z = z(t) и требуется определить скорость точки. Так как мы знаем, как определяется скорость точки при векторном способе задания ее движения, то перейдем от координатного способа задания ее движения к векторному: 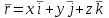 . (1) . (1)Продифференцируем обе части равенства (1) по времени и получим: 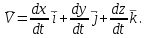 Полученный трехчлен есть формула разложения вектора скорости точки на составляющие по осям координат и из нее следует, что 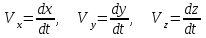 , ,то есть проекции скорости точки на оси координат равны первым производным по времени от соответствующих координат точки. Зная проекции скорости точки на оси координат, можно легко вычислить модуль скорости по формуле 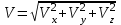 и определить направление вектора скорости по отношению к осям по направляющим косинусам  Ускорение точки при координатном способе задания ее движения По аналогии с определением скорости точки, для определения ускорения точки при координатном способе задания ее движения необходимо: Найти проекции ускорения точки на оси координат – они равны первым производным по времени от соответствующих проекций скорости точки или вторым производным по времени от соответствующих координат точки: 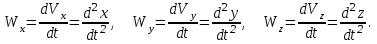 Вычислить модуль ускорения по формуле 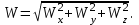 Определить направление вектора ускорения точки по направляющим косинусам: 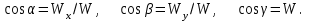 Скорость точки при естественном способе задания ее движения Пусть в момент времени t точка занимала положение М, определяемое расстоянием s, а по прошествии некоторого времени  , в момент времени t1 положение М1, определяемое расстоянием s1 (рисунок 6). , в момент времени t1 положение М1, определяемое расстоянием s1 (рисунок 6).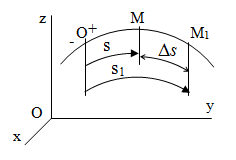 Рисунок 6 – Скорость точки при естественном способе задания движения Таким образом, за время  криволинейная координата точки получила приращение криволинейная координата точки получила приращение  . Если взять отношение . Если взять отношение  к к , то получим среднее значение численной величины скорости точки за время , то получим среднее значение численной величины скорости точки за время  : : 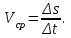 Переходя к пределу найдем численную скорость точки в данный момент времени: 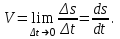 Итак, численная (алгебраическая) величина скорости точки в данный момент времени равна первой производной по времени от расстояния (криволинейной координаты):  Определяемая по этой формуле скорость называется алгебраической, поскольку имеет знак плюс или минус. Знак указывает в каком направлении отсчета расстояния s, положительном или отрицательном, движется в данный момент точка. Направляют вектор скорости точки по касательной к траектории ее движения с учетом ее знака. Ускорение точки при естественном способе задания ее движения В случае естественного способа задания движения точки ее ускорение определяют по его проекциям на естественные оси координат (касательную 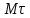 , нормальную , нормальную 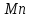 и бинормальную Mb оси). Эти оси имеют свое начало в данной точке М (они перемещаются вместе с нею) и образованы они пересечением граней естественного трехгранника (пересечением соприкасающейся, нормальной и спрямляющей плоскостей. и бинормальную Mb оси). Эти оси имеют свое начало в данной точке М (они перемещаются вместе с нею) и образованы они пересечением граней естественного трехгранника (пересечением соприкасающейся, нормальной и спрямляющей плоскостей.Разложим вектор скорости точки на составляющие по естественным осям координат с помощью единичных векторов этих осей 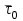 , , 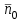 , , 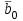 (Рисунок 7). (Рисунок 7).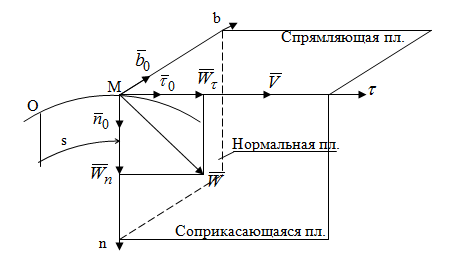 Рисунок 7 - Ускорение точки при естественном способе задания ее движения 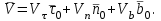 А также видно, что 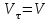 , а , а 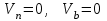 . .Тогда будет  Для определения ускорения обе части этого равенства продифференцируем по времени, учитывая, что V и 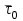 величины переменные, получим: величины переменные, получим: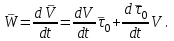 (2) (2)Преобразуем производную 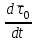 , ,представив ее как производную с промежуточным аргументом s - 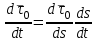 . .Далее применим формулу Френе  из курса дифференциальной геометрии. из курса дифференциальной геометрии.Тогда 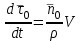 и формула (2) получит вид  (3) (3)Выражение (3) есть формула разложения вектора ускорения на составляющие по естественным осям координат. Из нее следует, что вектор ускорения точки всегда лежит в соприкасающейся плоскости и равен геометрической сумме касательного и нормального ускорений (бинормальное ускорение равно нулю). Следует также, что модули этих ускорений равны: 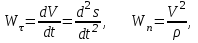 где 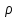 - радиус кривизны траектории точки в данный момент времени. - радиус кривизны траектории точки в данный момент времени. Таким образом, касательное ускорение точки равно первой производной по времени от алгебраической скорости точки или второй производной по времени от расстояния (криволинейной координаты) s. Нормальное ускорение точки равно квадрату скорости точки деленному на радиус кривизны ее траектории в данный момент времени. Касательное ускорение точки направлено по касательной к ее траектории в положительном или отрицательном направлениях отсчета расстояния s (в зависимости от его знака – оно может иметь знак плюс или минус, как и скорость). Нормальное ускорение точки всегда направлено к центру кривизны ее траектории (в положительном направлении нормальной оси). Модуль ускорения точки будет равен:  Учитывая расположение этих ускорений на чертеже. |
