Учебное пособие для студентов высших учебных заведений очного и заочного обучения
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
|
Лекция 3 Плоскопараллельное движение твердого тела, основные определения Упрощение изучения плоскопараллельного движения. Задание плоскопараллельного движения Разложение плоскопараллельного движения на поступательное и вращательное. Определение скорости точки плоской фигуры, движущейся в своей плоскости. Определение ускорения точки плоской фигуры, движущейся в своей плоскости. Плоскопараллельное движение твердого тела, основные определения Плоскопараллельным (плоским) называется такое движение твердого тела, при котором все его точки движутся в плоскостях параллельных некоторой неподвижной плоскости. Плоскопараллельное движение совершают многие детали механизмов и машин. Например, шатуны кривошипно-шатунных механизмов, шестерни планетарных и дифференциальных зубчатых передач, катки и колеса машин на прямолинейных участках пути. Упрощение изучения плоскопараллельного движения Рассмотрим тело D, совершающее плоскопараллельное движение относительно неподвижной плоскости движения  (рисунок 1). (рисунок 1).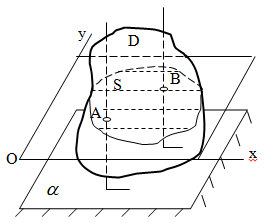 Рисунок 1 – Упрощение изучения плоскопараллельного движения Проведем в теле некоторую прямую перпендикулярную плоскости  . Все точки тела, лежащие на этой прямой будут двигаться тождественно, поскольку все они остаются в плоскостях параллельных плоскости . Все точки тела, лежащие на этой прямой будут двигаться тождественно, поскольку все они остаются в плоскостях параллельных плоскости  и расстояния между ними остаются неизменными (т.к. тело абсолютно твердое). и расстояния между ними остаются неизменными (т.к. тело абсолютно твердое).Следовательно, для изучения движения точек тела на этой прямой достаточно изучить движение только одной точки, например, точки А. Так, для изучения движения точек тела на второй прямой, показанной на рисунке, достаточно изучить движение точки В. Этот вывод будет справедлив для точек тела, лежащих на любой прямой перпендикулярной плоскости  . Если же все эти точки взять на одинаковом расстоянии от неподвижной плоскости, то можно прийти к следующему заключению: для упрощения изучения плоскопараллельного движения твердого тела надо рассечь его плоскостью параллельной плоскости движения, например Оху, и изучить движение точек полученной в результате сечения плоской фигуры S в плоскости этой фигуры. Чтобы охватить этим единым методом все многообразие частных случаев сечения плоскую фигуру представляют неограниченно большой. . Если же все эти точки взять на одинаковом расстоянии от неподвижной плоскости, то можно прийти к следующему заключению: для упрощения изучения плоскопараллельного движения твердого тела надо рассечь его плоскостью параллельной плоскости движения, например Оху, и изучить движение точек полученной в результате сечения плоской фигуры S в плоскости этой фигуры. Чтобы охватить этим единым методом все многообразие частных случаев сечения плоскую фигуру представляют неограниченно большой.Задание плоскопараллельного движения В силу отмеченного выше, положение тела при плоскопараллельном движении в любой момент времени может быть определено по положению плоской фигуры S относительно координат Оху. Положение же этой плоской фигуры можно определить по положению двух любых ее точек, например, точек А и В (рисунок 2). 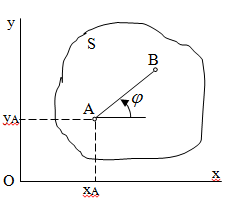 Рисунок 2 – Задание плоскопараллельного движения Одной точкой положение фигуры определить невозможно. Задачу можно заметно упростить, если эти точки соединить отрезком АВ и определять положение плоской фигуры по положению этого отрезка. Для чего достаточно задать положение одной его точки, например точки А, которую именуют полюсом, и угол 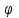 между этим отрезком и положительным направлением оси х, то есть тремя, зависящими от времени, параметрами: между этим отрезком и положительным направлением оси х, то есть тремя, зависящими от времени, параметрами: Эти равенства называются уравнениями (законом) плоскопараллельного движения твердого тела. Из них следует, что если координаты полюса А будут неизменны, то тело будет вращаться вокруг оси, проходящей через полюс перпендикулярно плоскости движения. Если же постоянным будет угол 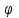 , то тело будет совершать поступательное движение. Следовательно, поступательное и вращательное движения тела есть частные случаи плоскопараллельного движения. , то тело будет совершать поступательное движение. Следовательно, поступательное и вращательное движения тела есть частные случаи плоскопараллельного движения.Разложение плоского движения на поступательное и вращательное Пусть плоская фигура в момент времени tбыла в положении 1, а в момент времени t1 переместилась в положение 2 (Рисунок 3). 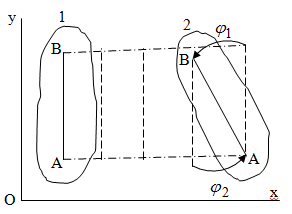 Рисунок 3 – Методика разложения плоского движения на поступательное и вращательное Перемещение фигуры из положения 1 в положение 2 можно представить следующим образом: 1.Принять за полюс точку А, переместить фигуру поступательно и совместить точки А, а затем повернуть ее вокруг полюса А на угол 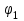 и совместить точки В; и совместить точки В;2.Принять за полюс точку В, переместить фигуру поступательно, а затем повернуть ее вокруг полюса В на угол 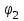 и совместить точки А. и совместить точки А.Таким образом, плоскопараллельное движение можно представить состоящим из суммы двух движений: поступательного движения тела со скоростью выбранного полюса и вращательного движения вокруг оси, проходящей через этот полюс перпендикулярно плоскости движения. Так как при поступательном движении фигура при разных полюсах должна за время  перемещения ее из одного положения в другое пройти разные расстояния, то поступательная часть движения зависит от выбора полюса. Вращательная же часть движения от выбора полюса не зависит, поскольку мы видим, что за время перемещения ее из одного положения в другое пройти разные расстояния, то поступательная часть движения зависит от выбора полюса. Вращательная же часть движения от выбора полюса не зависит, поскольку мы видим, что за время  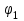 = = 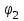 , следовательно будут равны друг другу и угловые скорости и угловые ускорения фигуры. , следовательно будут равны друг другу и угловые скорости и угловые ускорения фигуры.Скорость точки плоской фигуры, движущейся в своей плоскости Пусть плоская фигура S движется в своей плоскости Оху (рисунок 4). 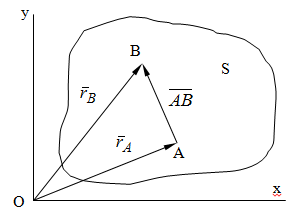 Рисунок 4 - Скорость точки плоской фигуры, движущейся в своей плоскости Примем некоторую точку А фигуры за полюс и определим скорость произвольной точки В фигуры. Для решения задачи зададим движение полюса А и точки В векторным способом (покажем на рисунке их радиус-векторы), а отрезку АВ дадим направление. Тогда, для любого момента времени, будет справедливо векторное равенство 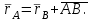 (1) (1)Продифференцируем по времени обе части этого векторного равенства: 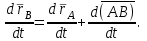 Отсюда, учитывая, что производная по времени от радиус-вектора точки равна вектору скорости точки и то, что 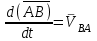 , ,то есть равна скорости точки во вращении ее (мгновенном) вместе с фигурой вокруг полюса А, получим 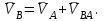 (2) (2)Таким образом, скорость любой точки плоской фигуры, движущейся в своей плоскости, равна геометрической сумме скорости точки фигуры, принятой за полюс, и скорости данной точки во вращении вместе с фигурой вокруг полюса. При решении практических задач за полюс принимается та точка, скорость которой известна или скорость которой можно определить по исходным данным. Заметим, что 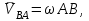 где 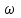 - угловая скорость фигуры. - угловая скорость фигуры.Ускорение точки плоской фигуры, движущейся в своей плоскости Для определения ускорения точки плоской фигуры воспользуемся формулой (2) предыдущего параграфа, а именно – обе ее части продифференцируем по времени, поскольку известно, что ускорение точки равно первой производной по времени от вектора ее скорости. Получим 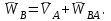 (3) (3)Следовательно, ускорение любой точки плоской фигуры, движущейся в своей плоскости, равно геометрической сумме ускорения точки фигуры, принятой за полюс, и ускорения данной точки во вращении вместе с фигурой вокруг полюса. Если принять во внимание, что 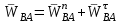 , ,то формула (3) получит вид: 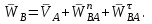 (4) (4)Нормальное и касательное ускорения точки В во вращении вокруг полюса А определяются по формулам: 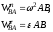 Направляют их так же, как соответствующие ускорения точек вращающегося тела. За полюс, при решении практических задач, принимается точка, ускорение которой задано или может быть определено по исходным данным. Модуль ускорения точки В определяют геометрически построением многоугольника из ускорений, входящих в равенство (4), или аналитическим методом по его проекциям на оси координат, которые определяют проектированием обеих частей векторного равенства (4) на оси координат. Лекция 4 Плоскопараллельное движение твердого тела. Теорема о проекциях скоростей двух точек плоской фигуры на прямую, проходящую через эти точки. Мгновенный центр скоростей. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей. Разные случаи определения положения мгновенного центра скоростей. Теорема о проекциях скоростей двух точек плоской фигуры на прямую, проходящую через эти точки Данная теорема имеет следующую формулировку: проекции скоростей двух точек плоской фигуры на прямую, проходящую через эти точки, равны друг другу. Рассмотрим доказательство теоремы. Возьмем две точки А и В плоской фигуры (рисунок 1). 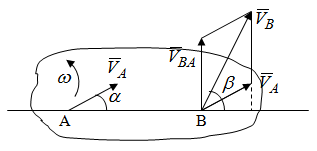 Рисунок 1 - Теорема о проекциях скоростей двух точек плоской фигуры Предположим, что точка А имеет скорость 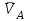 , а фигура имеет угловую скорость , а фигура имеет угловую скорость 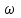 . Тогда, принимая точку А за полюс, можем записать. Что скорость точки В будет равна: . Тогда, принимая точку А за полюс, можем записать. Что скорость точки В будет равна: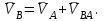 Далее изобразим это векторное равенство. Для этого спроектируем обе части этого векторного равенства на прямую, проходящую через точки А и В. Получим 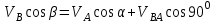 . .Так как cos 900 = 0, то окончательно будет 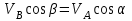 , ,что и требовалось доказать. Данная теорема позволяет легко определять скорость любой точки плоской фигуры, если известны скорость какой-либо другой точки фигуры, направления скоростей этих двух точек и углы, которые образуют векторы их скоростей с прямой, проходящей через эти две точки. Мгновенный центр скоростей Мгновенным центром скоростей называется точка плоской фигуры, скорость которой в данный момент времени равна нулю. Докажем, что такая точка существует. Пусть плоская фигура движется в своей плоскости и в данный момент известна скорость некоторой ее точки А по модулю и направлению и угловая скорость фигуры (рисунок 2). 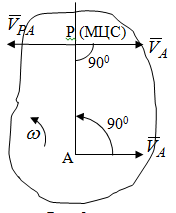 Рисунок 2 – Мгновенный центр скоростей произвольной фигуры Для определения положения мгновенного центра скоростей выполним следующее: вектор скорости точки А 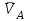 повернем в плоскости фигуры на 900 по ходу вращения фигуры и проведем вдоль него прямую, туда, куда он будет направлен после поворота; повернем в плоскости фигуры на 900 по ходу вращения фигуры и проведем вдоль него прямую, туда, куда он будет направлен после поворота;отложим от точки А в указанном направлении отрезок 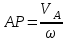 . .Точка Р будет мгновенным центром скоростей фигуры в данный момент времени. В самом деле, если точку А примем за полюс, то скорость точки Р 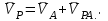 Нанесем векторы скоростей правой части этого равенства на чертеж (рис. 2). Как видно из чертежа, указанные скорости направлены вдоль одной прямой в разные стороны. Кроме того модуль скорости 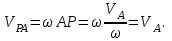 Тогда получается, что скорость точки Р равна нулю. Следовательно, она действительно есть мгновенный центр скоростей фигуры в данный момент времени. Необходимо иметь ввиду, что положение мгновенного центра скоростей постоянно изменяется, поскольку может изменяться модуль и направление скорости точки А, модуль и направление угловой скорости фигуры. С позиций понятия мгновенного центра скоростей плоскопараллельное движение можно трактовать как непрерывную серию мгновенных вращений тела вокруг оси, проходящей через мгновенный центр скоростей перпендикулярно плоскости движения тела. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей Зная положение мгновенного центра скоростей можно легко определить скорость любой точки плоской фигуры. В самом деле, принимая мгновенный центр скоростей Р за полюс (Рисунок 3), 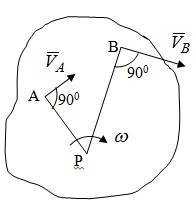 Рисунок 3 – Определение скоростей точек при использовании МЦС можно для двух произвольных точек А и В фигуры (рис. 3) написать, что 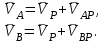 Учитывая, что 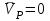 , получим: , получим: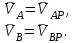 Таким образом, видим, что скорости произвольных точек А и В фигуры равны по модулю и направлению скоростям этих точек во вращении их вокруг мгновенного центра скоростей вместе с фигурой. Поэтому модули скоростей точек А и В можно выразить так: 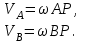 Разделив левые и правые части этих равенств друг на друга, будем иметь 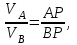 то есть, что скорости точек плоской фигуры пропорциональны их расстояниям от мгновенного центра скоростей (как и точек вращающегося тела). Из всего изложенного следует, что скорости точек тела при плоскопараллельном движении можно определять как скорости точек тела, вращающегося вокруг оси, проходящей через мгновенный центр скоростей перпендикулярно плоскости движения тела. Чтобы воспользоваться этим простым и эффективным способом определения скоростей точек тел, совершающих плоскопараллельное движение, нужно уметь определять положение мгновенный центр скоростей плоской фигуры. Разные случаи определения положения мгновенного центра скоростей Всего существует семь разных случаев определения положения мгновенного центра скоростей. В них исходят либо из механических условий ситуации, либо из того, что скорости точек плоской фигуры пропорциональны их расстояниям от мгновенного центра скоростей. Если тело катится без скольжения по неподвижной поверхности, то точка касания тела с поверхностью неподвижна и, следовательно, она будет мгновенным центром скоростей тела (Рисунок 4). 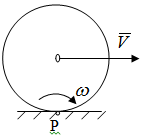 Рисунок 4 – Тело катится В основу такого заключения положены механические условия. В случае, когда известны направления скоростей двух точек плоской фигуры и эти скорости не параллельны между собой, то мгновенный центр скоростей находится в точке пересечения перпендикуляров, восстановленных в этих точках к их скоростям (Рисунок 5). 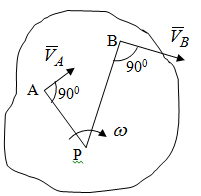 Рисунок 5 - Скорости не параллельны между собой Если скорости двух точек плоской фигуры перпендикулярны к отрезку, соединяющему эти точки, направлены в одну сторону и не равны друг другу по модулю, то мгновенный центр скоростей находится в точке пересечения прямых, проведенной через эти точки и проведенной через концы векторов скоростей этих точек (Рисунок 6). 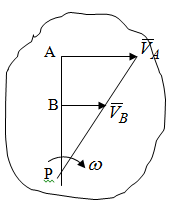 Рисунок 6 - Скорости двух точек плоской фигуры перпендикулярны к отрезку, соединяющему эти точки В случае, когда скорости двух точек тела антипараллельны и к отрезку, соединяющему эти точки перпендикулярны, мгновенный центр скоростей плоской фигуры находится в точке пересечения отрезка, соединяющего точки и прямой, проведенной через концы векторов скоростей этих точек (Рисунок 7).  Рисунок 7 - Скорости двух точек тела антипараллельны к отрезку Если известны модуль и направление скорости одной точки плоской фигуры и ее угловая скорость, то для определения положения мгновенного центра скоростей необходимо скорость точки повернуть в плоскости фигуры на 900 по ходу вращения фигуры и туда, куда она будет направлена провести по ней прямую. Затем на этой прямой в направлении повернутой скорости отложить отрезок, равный частному деления модуля скорости точки на угловую скорость фигуры (Рисунок 8). 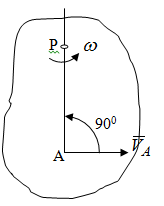 Рисунок 8 – МЦС при наличии угловой скорости 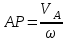 . .Полученная точка Р и будет мгновенным центром скоростей фигуры в данный момент времени. Если скорости двух точек плоской фигуры перпендикулярны к отрезку, соединяющему эти точки, направлены в одну сторону и равны по модулю, то мгновенный центр скоростей отсутствует, в этом случае его нет (Рисунок 9). 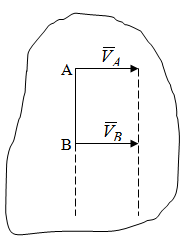 Рисунок 9 - Скорости двух точек плоской фигуры перпендикулярны к отрезку Действительно, если мы проведем прямые вдоль отрезка АВ и через концы векторов скоростей точек, то они будут параллельны и не пересекутся. В этом случае угловая скорость плоской фигуры будет равна нулю и все точки фигуры будут иметь равные по модулю и направлению скорости. Заметим, что ускорения точек фигуры будут разные. Если скорости двух точек плоской фигуры параллельны друг другу и к отрезку, соединяющему эти точки не перпендикулярны, то мгновенный центр скоростей у фигуры отсутствует (Рисунок 10). 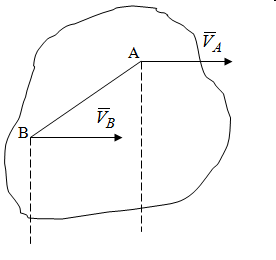 Рисунок 10 – Скорости двух точек плоской фигуры параллельны друг другу и не перпендикулярны к отрезку, соединяющему эти точки В самом деле, если мы попробуем действовать так, как в случае 2, то увидим, что перпендикуляры, восстановленные в точках к их скоростям не пересекаются, поскольку параллельны друг другу. В этом случае, как и в предыдущем, угловая скорость фигуры равна нулю и все точки ее имеют равные по модулю и направлению скорости (но ускорения точек будут разные). Лекция 5 Сложное движение точки. Основные понятия и определения. Теорема сложения скоростей. Теорема сложения ускорений (теорема Кориолиса). Модуль и направление ускорения Кориолиса, случаи его отсутствия. Физические причины возникновения ускорения Кориолиса. Сложное движение точки. Основные понятия и определения Сложным, или составным, называется такое движение точки, которое мысленно можно представить, как сумму двух движений: движения точки относительно подвижной системы координат и движения точки вместе с подвижной системой координат относительно неподвижной (Рисунок 1). 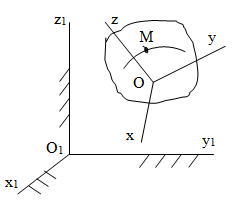 Рисунок 1 – Задание сложного движения точки Сложное движение совершают многие точки деталей машин. Например, любая точка грабли мотовила жатки комбайна вращается вокруг оси мотовила и одновременно перемещается с жаткой относительно поверхности поля; человек, если принять его за точку, может перемещаться по салону автобуса и, одновременно с этим, перемещаться вместе с автобусом. Прежде, чем приступить к определению кинематических характеристик движения точки введем ряд понятий. Движение точки относительно подвижной системы координат называется относительным. Скорость и ускорение точки в этом движении называются относительными и обозначаются 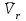 и и 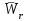 соответственно. соответственно.Движение точки вместе с подвижной системой координат по отношению к неподвижной системе координат называется переносным. Скорость и ускорение точки (той точки подвижной системы координат, с которой совпадает данная точка) в этом движении называются переносными и обозначаются 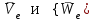 соответственно. соответственно.Движение точки по отношению к неподвижной системе координат непосредственно называется абсолютным или сложным. Скорость и ускорение точки в этом движении называются абсолютными и обозначаются 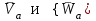 соответственно. Они определяются по теоремам сложения скоростей и ускорений. соответственно. Они определяются по теоремам сложения скоростей и ускорений.Прежде, чем перейти к рассмотрению этих теорем заметим, что для наблюдения и изучения относительного движения точки надо мысленно остановить ее переносное движение и, наоборот, для наблюдения и изучения переносного движения точки надо мысленно остановить ее относительное движение. Теорема сложения скоростей Суть этой теоремы состоит в следующем: абсолютная скорость точки в сложном движении равна геометрической сумме ее переносной и относительной скоростей, то есть 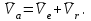 Рассмотрим доказательство теоремы. Пусть точка М совершает сложное движение, состоящее из относительного движения в подвижной системе координат Оxyz и переносного движения точки вместе с этой системой координат по отношению неподвижной системы координат О1x1y1z1 (рис. 2). 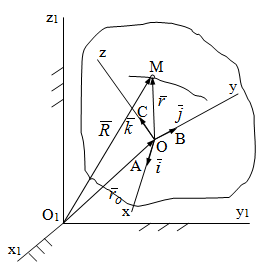 Рисунок 2 – Доказательство теоремы сложения скоростей Зададим движение точки векторным способом: относительное движение радиус-вектором 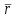 , переносное движение радиус-вектором , переносное движение радиус-вектором  , абсолютное движение радиус-вектором , абсолютное движение радиус-вектором  . Как следует из чертежа . Как следует из чертежа (1) (1)Разложим радиус-вектор  на составляющие по подвижным осям координат с помощью единичных векторов на составляющие по подвижным осям координат с помощью единичных векторов  , , , ,  этих осей: этих осей:  . Тогда уравнение (1) абсолютного движения точки М получит вид . Тогда уравнение (1) абсолютного движения точки М получит вид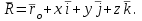 (2) (2)Теперь рассмотрим относительное движение точки М. Для этого мысленно остановим переносное движение (подвижную систему координат). Тогда величины 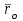 , , 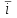 , ,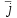 , , 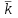 будут постоянными и, дифференцируя по времени обе части равенства (2) получим относительную скорость точки: будут постоянными и, дифференцируя по времени обе части равенства (2) получим относительную скорость точки: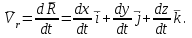 (3) (3)Рассмотрим переносное движение точки М, для чего мысленно остановим относительное движение точки (ее движение относительно подвижной системы координат). Тогда величины x, y, z будут постоянными и, дифференцируя обе части равенства (2) по времени получим переносную скорость точки: 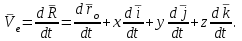 (4) (4)И, наконец, рассмотрим абсолютное движение точки. Продифференцируем по времени обе части равенства (2), учитывая, что все величины в его правой части переменные, получим выражение абсолютной скорости точки М: 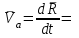 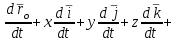 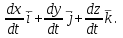 (5) (5)С учетом выражений (3) и (4) из равенства (5) следует, что 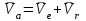 , (6) , (6)что требовалось доказать. Итак, вектор абсолютной скорости точки геометрически равен диагонали параллелограмма, построенного на векторах переносной и относительной скоростей (Рисунок3). 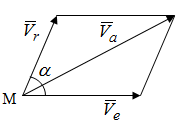 Рисунок 3 – Построение параллелограмма на векторах переносной и относительной скоростей Поэтому модуль абсолютной скорости точки можно определить, как длину этой диагонали, по формуле:  . .Кроме того, при решении задач часто модуль абсолютной скорости точки определяют по ее проекциям на оси координат (  ), ),для чего векторы  и и  показывают на чертеже, а затем обе части равенства (6) проектируют на координатные оси, которые также показывают на чертеже. показывают на чертеже, а затем обе части равенства (6) проектируют на координатные оси, которые также показывают на чертеже.Теорема сложения ускорений (теорема Кориолиса) Данная теорема гласит, что абсолютное ускорение точки в сложном движении равно геометрической сумме ее переносного, относительного и кориолисова ускорений: 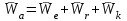 . .Для доказательства теоремы воспользуемся рис. 2 и формулами, полученными при доказательстве теоремы о сложении скоростей. Для определения относительного ускорения точки обе части равенства (3) продифференцируем по времени. Получим: 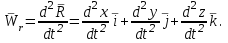 (7) (7)Дифференцируя по времени обе части равенства (4) получим выражение переносного ускорения точки: 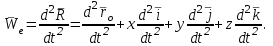 (8) (8)А теперь, для определения абсолютного ускорения точки, продифференцируем по времени дважды обе части уравнения (2), учитывая, что все величины в правой его части переменные: 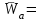 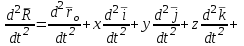 + 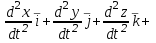 + 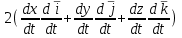 . (9) . (9)Преобразуем правую часть этого равенства. Первые четыре слагаемые правой части равенства (9) есть, согласно (8), переносное ускорение точки. Последующие три слагаемые, согласно выражения (7), есть относительное ускорение точки. Остается выяснить что дает удвоенная скобка. Имеющиеся в ней производные по времени от координат x, y, z есть проекции относительной скорости точки на оси координат: 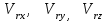 , а производные по времени от единичных векторов , а производные по времени от единичных векторов  , , , ,  подвижных осей координат есть скорости точек А, В, С, расположенных на концах этих векторов (рис. 2). Скорости же, указанные точки, получают в результате вращения подвижных осей координат (модули этих векторов постоянны - равны единице) вокруг начала О этих осей . Поэтому скорости точек А, В, С можно выразить по формуле Эйлера для линейной скорости точки вращающегося тела. (см. лекцию № 2 по кинематике): подвижных осей координат есть скорости точек А, В, С, расположенных на концах этих векторов (рис. 2). Скорости же, указанные точки, получают в результате вращения подвижных осей координат (модули этих векторов постоянны - равны единице) вокруг начала О этих осей . Поэтому скорости точек А, В, С можно выразить по формуле Эйлера для линейной скорости точки вращающегося тела. (см. лекцию № 2 по кинематике): . .Подставим оговоренные значения величин в удвоенную скобку и проведем ее преобразование: 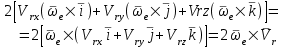 Размерность полученного результата будет 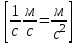 . .Следовательно, удвоенная скобка есть ускорение. Это дополнительное (к относительному и переносному) ускорение обозначается 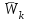 и называется ускорением Кориолиса (по имени французского ученого Гюстава Гаспара Кориолиса, доказавшего эту теорему в 1831 г.): и называется ускорением Кориолиса (по имени французского ученого Гюстава Гаспара Кориолиса, доказавшего эту теорему в 1831 г.):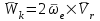 . (10) . (10)С учетом всего изложенного о правой части равенства (9) оно получает вид 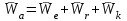 , (11) , (11)что и требовалось доказать. Модуль и направление ускорения Кориолиса, случаи его отсутствия Из выражения (10) следует, что ускорение Кориолиса равно удвоенному векторному произведению вектора угловой переносной скорости на вектор относительной скорости точки. Следовательно, его модуль определяется, как модуль векторного произведения двух векторов: 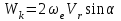 , (12) , (12)где 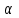 - угол между векторами - угол между векторами 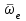 и и 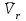 . .Направление ускорения Кориолиса определяется по правилу Н.Е. Жуковского: для определения направления ускорения Кориолиса необходимо относительную скорость точки проектировать на плоскость перпендикулярную оси переносного вращения, а затем эту проекцию повернуть в этой плоскости на 900 по ходу переносного вращения; ее направление, после этого, будет направлением ускорения Кориолиса (Рисунок 4). 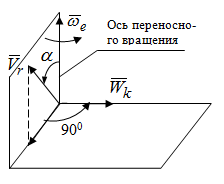 Рисунок 4 - Модуль и направление ускорения Кориолиса Направление ускорения Кориолиса можно установить также, исходя непосредственно, из определения векторного ускорения двух векторов. Рассмотрим случаи отсутствия ускорения Кориолиса. Как следует из анализа формулы (12) модуля ускорения Кориолиса оно будет равно нулю в следующих случаях: Когда угловая скорость переносного вращения 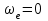 , то есть тогда, когда переносное движение будет поступательным или будет менять направление вращения; , то есть тогда, когда переносное движение будет поступательным или будет менять направление вращения;Когда относительная скорость точки 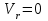 ; ;Когда угол  между векторами между векторами  и и  равен нулю или 1800, то есть в случае, когда относительная скорость точки параллельна оси переносного вращения. равен нулю или 1800, то есть в случае, когда относительная скорость точки параллельна оси переносного вращения.Физические причины возникновения ускорения Кориолиса Физические причины возникновения ускорения Кориолиса заключаются в изменении относительной скорости точки ее переносным движением и изменении переносной скорости точки ее относительным движением. Так, ползун В, движущийся по вращающемуся стержню ОА, совершает сложное движение, состоящее из относительного движения по стержню со скоростью  и переносного вращения вместе со стержнем со скоростью и переносного вращения вместе со стержнем со скоростью 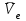 (Рисунок 5). (Рисунок 5).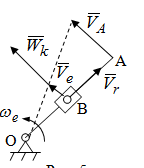 Рисунок 5 – Ползун в сложном движении При этом переносное движение изменяет относительную скорость по направлению, а относительное движение, изменяя положение ползуна на стержне – расстояние ОВ, изменяет модуль переносной скорости ( 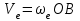 ). В результате возникает ускорение Кориолиса. ). В результате возникает ускорение Кориолиса.Лекция 6 Сложное движение твердого тела. Сложение поступательных движений. Сложение двух, направленных в одну сторону, вращений вокруг параллельных осей. Сложение двух, направленных в разные стороны и имеющих разные угловые скорости, вращений вокруг параллельных осей. Сложение двух, направленных в разные стороны и имеющих одинаковые угловые скорости, вращений вокруг параллельных осей. Сложение двух вращений вокруг пересекающихся осей. Сложение поступательного и вращательного движений. Сложное движение твердого тела Сложным называется такое движение твердого тела, при котором оно одновременно движется относительно подвижной системы координат и вместе с нею переносится относительно неподвижной системы координат. Возможны разные случаи сочетаний движений тела. Сложение поступательных движений В этом случае все точки тела в относительном движении имеют одинаковые по модулю и направлению скорости 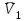 , а в переносном движении равные по модулю и направлению скорости , а в переносном движении равные по модулю и направлению скорости  . Стало быть в каждый момент времени все точки тела имеют равные по модулю и направлению абсолютные скорости . Стало быть в каждый момент времени все точки тела имеют равные по модулю и направлению абсолютные скорости  , ,а это значит, что результирующее (абсолютное) движение тела будет поступательным с указанной скоростью. Сложение двух, направленных в одну сторону, вращений тела вокруг параллельных осей Пусть тело вращается вокруг оси z с угловой скоростью  , а вокруг оси z1 c угловой скоростью , а вокруг оси z1 c угловой скоростью  (Рисунок 1). (Рисунок 1).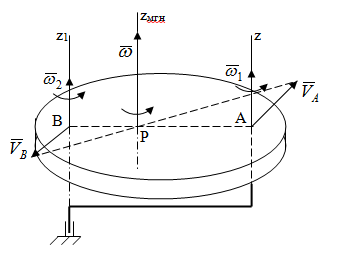 Рисунок 1 - Сложение двух, направленных в одну сторону, вращений тела вокруг параллельных осей Вполне очевидно, что точка А, лежащая на оси z, будет получать скорость от вращения тела вокруг оси z1, а точка В получать скорость от вращения тела вокруг оси z и эти скорости будут равны: 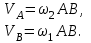 Проведем через концы векторов скоростей этих точек прямую и точка Р ее пересечения с отрезком АВ будет мгновенным центром скоростей. Следовательно результирующее движение тела будет мгновенным вращательным вокруг оси, проходящей через точку Р. Найдем абсолютную угловую скорость. 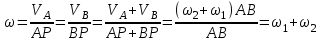 . .Как видим, абсолютная угловая скорость определяется аналогично равнодействующей двух параллельных сил. Следовательно, по аналогии с силами, ось мгновенного вращения делит отрезок АВ на части обратно пропорциональные угловым скоростям складываемых вращений, внутренним образом: 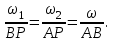 Таким образом, при сложении двух, направленных в одну сторону, вращений тела вокруг параллельных осей, результирующее движение будет мгновенным вращательным, направленным в ту же сторону, что и складываемые вращения. Ось мгновенного вращения параллельна осям складываемых вращений и делит расстояние между ними на части обратно пропорциональные угловым скоростям этих вращений внутренним образом. Абсолютная угловая скорость равна сумме угловых скоростей складываемых вращений. Сложение двух, направленных в разные стороны и имеющих разные угловые скорости, вращений тела вокруг параллельных осей Для определенности будем полагать, что 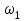 > >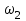 (Рисунок 2). (Рисунок 2). Рисунок 2 – Сложение двух, направленных в разные стороны и имеющих разные угловые скорости, вращений тела вокруг параллельных осей Покажем на чертеже скорости точек А и В – они перпендикулярны к отрезку АВ и числено они равны:  . .Проведем прямые через точки А и В и через концы векторов скоростей этих точек, точка их пересечения Р будет мгновенным центром скоростей. Тело будет совершать мгновенное вращение вокруг оси, проходящей через эту точку, в сторону вращения с большей угловой скоростью. Найдем абсолютную угловую скорость. Получен результат, как и при сложении двух антипараллельных векторов. Из всего изложенного можно сделать следующие выводы: при сложении двух, направленных в разные стороны и имеющих разные угловые скорости, вращений тела вокруг параллельных осей, результирующее движение будет мгновенным вращательным с угловой скоростью, равной разности угловых скоростей складываемых вращений и направленным в сторону вращения, имеющего большую угловую скорость. Ось мгновенного вращения параллельна осям складываемых вращений и делит расстояние между ними на части обратно пропорциональные их угловым скоростям внешним образом. Сложение двух, направленных в разные стороны и имеющих одинаковые угловые скорости, вращений тела вокруг параллельных осей Такое сочетание вращений называется парой вращений, а векторы их угловых скоростей образуют пару угловых скоростей (Рисунок 3). 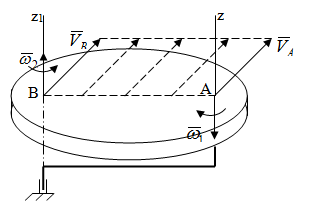 Рисунок 3 - Сложение двух, направленных в разные стороны и имеющих одинаковые угловые скорости, вращений тела вокруг параллельных осей Скорости точек А и В будут равны друг другу и по направлению, и по модулю: 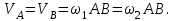 Следовательно мгновенного центра скоростей нет, все точки тела имеют такие же, как и точки А и В, скорости и тело совершает поступательное движение. Общий вывод: при сложении двух, направленных в разные стороны и имеющих одинаковые угловые скорости, вращений вокруг параллельных осей, результирующее движение тела будет поступательным, со скоростью, равной произведению любой из угловых скоростей на расстояние между данными осями. Направлена эта скорость будет перпендикулярно плоскости, проходящей через данные оси, в ту сторону, откуда поворот пары угловых скоростей складываемых вращений виден против хода часовой стрелки. Сложение двух вращений тела вокруг пересекающихся осей В этом случае скорость точки О тела, как лежащей одновременно на двух осях вращения, одна из которых неподвижна, будет равна нулю (Рисунок 4). 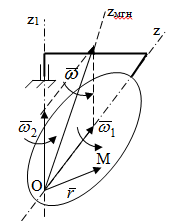 Рисунок 4 – Сложение двух вращений тела вокруг пересекающихся осей Это значит, что тело будет совершать мгновенное вращение вокруг оси, проходящей через точку О пересечения осей. Для определения абсолютной угловой скорости вычислим абсолютную скорость произвольной точки М тела. Положение точки М зададим радиус-вектором 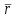 . Абсолютная скорость точки согласно теореме о сложении скоростей равна геометрической сумме ее относительной и переносной скоростей: . Абсолютная скорость точки согласно теореме о сложении скоростей равна геометрической сумме ее относительной и переносной скоростей: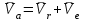 . .Поскольку и относительное, и переносное движения вращательные, то их скорости можно выразить по формуле Эйлера: 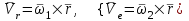 . .Тогда, абсолютная скорость точки 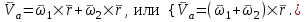 С другой стороны, 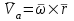 , где , где 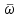 - абсолютная угловая скорость тела. - абсолютная угловая скорость тела.Из сравнения двух последних равенств следует, что 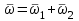 . .Так как вектор угловой скорости расположен на оси вращения, то из этой формулы вытекает также, что ось мгновенного вращения будет направлена вдоль вектора 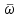 абсолютной угловой скорости тела. Эта ось, заметим, будет описывать конусную поверхность с вершиной в точке О. абсолютной угловой скорости тела. Эта ось, заметим, будет описывать конусную поверхность с вершиной в точке О.Итак, при сложении двух вращений тела вокруг пересекающихся осей, результирующее движение тела будет мгновенным вращательным вокруг оси, проходящей через точку пересечения осей. Абсолютная угловая скорость будет равна геометрической сумме угловых скоростей складываемых вращений. Ось мгновенного вращения направлена вдоль вектора абсолютной угловой скорости и с течением времени описывает коническую поверхность с вершиной в точке пересечения осей. Сложение поступательного и вращательного движений При сложении указанных движений, в зависимости от расположения скорости 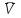 поступательного движения и вектора угловой скорости поступательного движения и вектора угловой скорости  вращательного движения, возможны три разных случая: вращательного движения, возможны три разных случая:Первый случай. Указанные скорости перпендикулярны друг другу (Рисунок 5).  Рисунок 5 – Сложение поступательного и вращательного движения (первый случай) В этом случае все точки тела, как видно из рис. 5, будут двигаться в плоскостях, параллельных некоторой неподвижной плоскости и тело будет совершать плоскопараллельное движение. Это же движение можно рассматривать, как состоящее из серий мгновенных вращений вокруг оси, проходящей через мгновенный центр скоростей Р. причем, как известно, расстояние  . .Второй случай. Векторы  и и  направлены вдоль одной прямой (Рисунок 6). направлены вдоль одной прямой (Рисунок 6).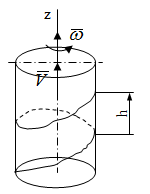 Рисунок 6 - Сложение поступательного и вращательного движения (второй случай) То есть тело вращается вокруг оси и одновременно движется поступательно вдоль оси. Такое движение тела называется винтовым. Ось, проведенная вдоль вектора 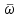 (ось вращения тела) называется осью винта. Если векторы (ось вращения тела) называется осью винта. Если векторы 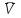 и и 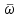 направлены в одну сторону, то винт называют правым, а если в разные, то левым. направлены в одну сторону, то винт называют правым, а если в разные, то левым.Все точки тела, не лежащие на оси вращения, движутся по кривым, называемым винтовыми линиями. Расстояние h, проходимое точкой вдоль оси винта за один оборот тела называется шагом винта. Шаг винта  , ,где Т – время одного оборота тела вокруг оси винта. При равномерном вращении тела  , ,а поэтому шаг винта  . .Из этой формулы видно, что для того, чтобы шаг винта был постоянным необходимо, чтобы  и и  были постоянными. были постоянными.Третий случай. Векторы  и и  образуют произвольный угол образуют произвольный угол  (Рисунок 7). (Рисунок 7). Рисунок 7 - Сложение поступательного и вращательного движения (третий случай) Для определения абсолютного (результирующего) движения тела разложим вектор  скорости поступательного движения тела на две составляющие: скорости поступательного движения тела на две составляющие:  - параллельную оси z и - параллельную оси z и  - перпендикулярную этой оси. Затем скорость - перпендикулярную этой оси. Затем скорость  заменим парой угловых скоростей заменим парой угловых скоростей  и и  , равных по модулю , равных по модулю  с плечом с плечом  . .Векторы  и и  в сумме дают ноль – их отбросим. В результате у тела останется поступательное движение вдоль оси Рz1 cо скоростью в сумме дают ноль – их отбросим. В результате у тела останется поступательное движение вдоль оси Рz1 cо скоростью  = =  cosα и вращательное движение вокруг этой оси (мгновенного вращения) с угловой скоростью ω. cosα и вращательное движение вокруг этой оси (мгновенного вращения) с угловой скоростью ω.Следовательно, результирующее движение будет мгновенным винтовым вокруг оси Рz1 винта, непрерывно изменяющей свое положение. Контрольные вопросы к разделу «Кинематика» 1. Что называется кинематикой? 2. Что понимается под механическим движением? 3. Что называется телом отсчета? 4. Что такое “система отсчета”? 5. Можно ли изучать механическое движение твердого тела без указания системы отсчета? 6. В чем состоит относительность механического движения? 7. Как трактуется пространство в классической механике? 9. Какими моделями представляют тела в кинематике? 10. На какие части делится кинематика? 11. Какие задачи решаются в кинематике точки? 12. Какие задачи решаются в кинематике твердого тела? 13. Что значит “задать движение” точки или твердого тела? 14. Что называется траекторией точки? 15. Что называется скоростью точки? 16. Что называется ускорением точки? 17. Какими способами задается движение точки? 18. В чем состоит координатный способ задания движения точки? 19. В чем заключается естественный способ задания движения точки? 20. В чем состоит векторный способ задания движения точки? 21. Какой зависимостью связаны между собой векторный и координатный способы задания движения точки? 22. Какой зависимостью связаны между собой естественный и координатный способы движения точки? 23. Как определяют траекторию точки при координатном способе зада-ния ее движения? 24. Как определяют траекторию точки при векторном способе задания ее движения? 25. Чему равна скорость точки при векторном способе задания ее движения? 26. Как по отношению к траектории направлена скорость точки? 27. Чему равно ускорение точки при векторном способе задания ее движения? 28. Как определяют скорость точки при координатном способе задания ее движения? 29. Как определяется ускорение точки при координатном способе задания ее движения? 30. Как определяют скорость точки при естественном способе задания ее движения? |
