|
|
Теоретико-игровые методы принятия решений (Еремеев А. П.). Теоретико-игровые методы принятия решений (Еремеев А. П. Учебное пособие по курсам Теория игр и исследование операций, Теория принятия решений
1.ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИГР.
КЛАССИФИКАЦИЯ ИГРОВЫХ МОДЕЛЕЙ
Игрой (теоретико-игровой моделью) называется упрощённая формализованная модель конфликтной ситуации, а конфликтующие стороны называются игроками.
Ситуация называется конфликтной, если в ней сталкиваются интересы двух или более сторон, преследующих различные (в частном случае противоположные) цели.
Однократный розыгрыш игры от начала и до конца называется партией игры.
Результатом партии являются платежи (выигрыши или проигрыши игроков).
Игра состоит из ходов, заключающихся в выборе игроками из некоторого множества возможных альтернатив.
Ходы могут быть личными или случайными. Личный ход – ход, при котором игрок осуществляет сознательный выбор. Случайный ход – ход, выбор варианта в котором осуществляется некоторым механизмом случайного выбора (бросание монеты, кости и т. п.).
Игра, в которой присутствуют личные ходы, возможно, наряду со случайными, называется стратегической. Игра, состоящая из одних случайных ходов, называется азартной.
Задачей теории игр является нахождение оптимальных стратегий игроков – правил, обеспечивающих максимизацию выигрыша или минимизацию проигрыша игрока в стратегических играх. Множество стратегий игрока должно быть полным (всеобъемлющим), т.е. определять выбор игрока в любой возможной ситуации игры.
Чисто азартные игры относятся к компетенции теории вероятностей и математической статистики.
Определение 1.1. Стратегическая игра n лиц (сторон) может быть задана набором {A1, …,An,H(A1, …,An)}, где – Ai, i=1, …,n, – стратегия i го игрока, H – платёж игры, т.е. выигрыши (или проигрыши) игроков.
1.2.Классификация игровых моделей
Классификация теоретико-игровых моделей представлена на рис. 1.1.
В зависимости от дискретности или непрерывности множества стратегий игры соответственно делятся на дискретные или непрерывные,причем дискретные игры в зависимости от конечности или бесконечности множества стратегий могут быть соответственно конечными или бесконечными, непрерывные игры – всегда бесконечные.
В зависимости от числа участвующих в игре игроков игры бывают N лиц, которые в зависимости от того, разрешены коалиции (кооперации) игроков или нет, могут быть соответственно коалиционными (кооперативными) или некоалиционными (некооперативными), или 2-х лиц (парными), которые в зависимости от суммарной величины платежа могут быть антагонистическими, если суммарный платеж игроков равен нулю, или неантагонистическими, если суммарный платеж не равен нулю. Заметим, что в антагонистической игре интересы игроков строго противоположны, т.е. выигрыш одного игрока в точности равен проигрышу другого, а в неантагонистической – просто не совпадают, что ведет к ситуации, когда увеличение выигрыша одного игрока ведет к уменьшению выигрыша другого.
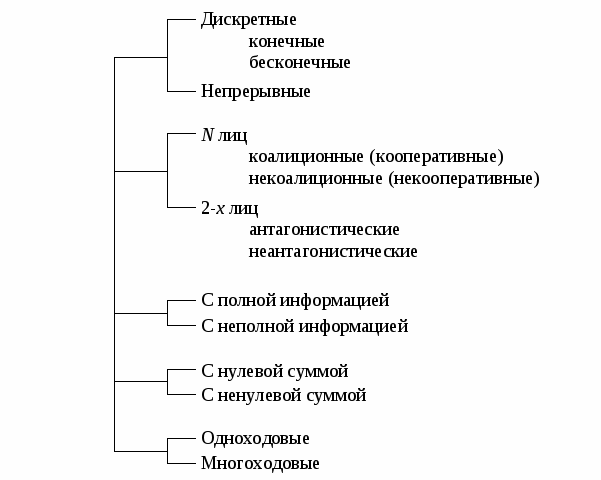
Рис. �1�.1. Классификация теоретико-игровых моделей
Игра называется игрой с полной информацией, если игрокам известна вся предыстория игры, т.е. все личные и случайные ходы противников (противника), в противном случае имеем игру с неполной информацией.
В зависимости от суммарного платежа игроков игры делятся на игры с нулевой суммой, если суммарный платеж равен нулю, и с ненулевой суммой, в противном случае. Примером игры с нулевой суммой является парная антагонистическая игра.
И, наконец, в зависимости от числа ходов в партии игры могут быть одноходовые и многоходовые.
Наиболее разработанными в теории игр являются модели игр 2-х лиц с нулевой суммой (антагонистических игр).
1.3.Контрольные вопросы к разделу 1
Сформулируйте понятие игры как модели конфликтной ситуации.
Сформулируйте основную задачу теории игр.
Дайте определение стратегической игры n лиц (сторон).
Приведите классификацию теоретико-игровых моделей.
Какие игры называются антагонистическими и неантагонистическими, с полной и неполной информацией?
Модели каких игр являются наиболее разработанными в теории игр?
|
|
|
 Скачать 1.18 Mb.
Скачать 1.18 Mb.
