Пономаренко-Математика. Кратные интегралы. Учебное пособие предисловие данное учебное пособие предназначено для студентов немате

• Название: Учебное пособие предисловие данное учебное пособие предназначено для студентов немате
• Дата: 27.03.2023
• Размер: 0.93 Mb.
• Имя файла: Пономаренко-Математика. Кратные интегралы.docx
• Тип: Учебное пособие; #1019168
• страница: 10 из 17

∫∫∫
Замена переменных в тройном интеграле
В интеграле f(x,y,z)dxdydz замена переменных интегриро-

(V)

вания влечет переход от переменных x, y, zк новым переменным

интегрирования u, v, w, связанным со старыми соотношениями

^⎧⎪_⎨x= x(u,v,w),
y= y(u,v,w),

^⎪⎩z= z(u,v,w).

Система (10) представляет собой отображение Φ =

(10)


⎛ ⎞

⎝ ⎠
x(u,v, w)

y(u,v,w)

z(u,v,w)

некоторой замкнутой ограниченной области (ν) в пространстве O₁uvwна замкнутую ограниченную область (V ) в пространстве Oxyz(рис. 27).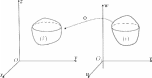





Рис.27
Если выполняются условия:

1. 
   отображение (10) взаимно однозначно;
   
2. 
   функции x(u,v,w),y(u,v,w),z(u,v,w) в (10) непрерывно диффе- ренцируемы в (ν);
   

3. 
   якобиан отображения (10)
   

..
∂x∂x


.
∂u ∂vJ(u,v,w) = ^{∂y ∂y}

∂u ∂v

∂z∂z

^. ∂u ∂v

∂x


..
∂w

^∂y = 0 в (ν),


..
∂w

∂z

∂w

∫∫∫
то имеет место формула⁹


∫∫∫
(V)

f(x,y,z) dxdydz=

=

(ν)

f(x(u,v,w),y(u,v,w),z(u,v,w)) |J(u,v,w)| dudvdw.(11)

⎧_⎪⎨
При этих условиях существует обратное отображение Φ⁻¹ : (V) →(ν),

⎛ ⎞−

⎝ ⎠
u(x,y,z)

Φ ¹ = v(x,y,z) , т. е.

w(x,y,z)

u= u(x,y,z),

v= v(x,y,z),

^⎩⎪w= w(x,y,z).


(12)

Далее, ∀N∈ (ν), N(u,v,w) −→ M(x(u,v,w), y(u,v,w),


∈
z(u, v, w)), M(V ); u, v, wназываются криволинейными коорди-натамиточки M¹⁰.


∈
Поверхности u(x, y, z) = const, v(x, y, z) = const, w(x, y, z) = const называются координатнымиповерхностями. Через каждую точку M области (V ) проходят три координатные поверхности u = const, v = const, w = const. (Аналогично для каждой точки N(ν).)

Линии

v= const

w= const

_, u= const



w= const

_, u= const



v= const

⁹ Доказательство этого утверждения желательно изучить самостоятельно, используя учебники, например [1].

¹⁰ Криволинейные координаты u,v,wзаписывают так же, как и декартовы (в

круглых скобках рядом с точкой: M(u,v,w)).

∈
называются координатнымилиниямикоординат u, v, wсоответ- ственно. Через каждую точку Mобласти (V ) проходят три коор- динатные линии координат u, v, w. (Аналогично для каждой точки N(ν)).

В качестве примеров криволинейных координат приведем ци- линдрические и сферические координаты.