Пономаренко-Математика. Кратные интегралы. Учебное пособие предисловие данное учебное пособие предназначено для студентов немате
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
ПОНЯТИЕ О МНОГОКРАТНЫХ ИНТЕГРАЛАХРассмотренные ранее двойной и тройной интегралы являются частными случаями n-кратного интеграла Римана (как и однократ- ∫ ный интеграл b тоже (при )). f(x)dx n= 1 a ∈ Общая схема введения таких интегралов следующая: Пусть на некотором ограниченном множестве Ω задана функция f (A), AΩ. Разобьем Ω на Nчастей ΔΩj,j = 1, 2,...,N , обозначим λранг разбиения, характеризующий максимальные размеры частичных областей, в каждой части ΔΩjвыберем произвольную точку Aj и составим сумму N Σ j=1 f(Aj)Δσj , где Δσj — мера (длина, площадь, объем и т. д.) частичной области ΔΩj11. Будем разбивать Ω на все более и более мелкие части так, чтобы N−→→∞ λ 0. Если существует lim λ→0 j=1 f(Aj)Δσj, не зависящий ни от ΣN способа разбиения Ω на части, ни от выбора точек Ajв каждой из этих частей, то он называется интегралом функции f по области интегрирования Ω. Прежде чем вводить n-кратный интеграл, следует определить объем области в пространстве Rn. Прежде всего вводится объем прямоугольного параллелепипеда в Rn. ПрямоугольнымпараллелепипедомвRnназывается множество D= {x(x1,x2,...,xn)| aj≤ xj≤ bj,aj,bj∈ R,j= 1,2,...,n}. Его объемомназывается произведение n j=1 (bj− aj). Объединение прямоугольных параллелепипедов, у каждой пары которых нет об- щих внутренних точек, имеет объем, равный сумме объемов всех параллелепипедов, входящих в это объединение. ∈ Пусть теперь имеется область (V) Rn. Впишем в (V) «ступен- чатую» фигуру, являющуюся объединением прямоугольных парал- лелепипедов, «примыкающих» друг к другу своими гранями и не имеющих общих внутренних точек (рис. 35 для n= 2). 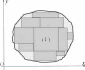 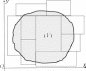 Рис.35 Рис.36 Обозначим множество объемов всех таких ступенчатых фигур {Vi}.Обозначимдалее V∗ = sup Vi.(Супремум берется по объемам 11 О других мерах можно узнать, например, из книг по теории функций ве- щественного аргумента, функциональному анализу, в частности из [3]. всевозможных таких вписанных фигур.) V∗ называется внутрен-нимобъемом области (V ). Аналогично рассматриваются всевоз- можные ступенчатые фигуры, «описанные» около (V) (рис. 36 для n = 2). Множество их объемов обозначим {Ve}. Далее вводится обо- значение V ∗ = inf{Ve}. V ∗ называется внешним объемом области (V). Если V∗ = V∗, то это число и называют объемомобласти(V). Теперь можно ввести n-кратный интеграл. Пусть (V ) — ограни- ченная область в пространстве Rn, имеющая объем. Пусть на (V ) задана функция f(x), x(x1,x2,...,xn) ∈ (V). Разобьем (V) на N частей (ΔVj),j= 1,2,...,N. Обозначим: dj= sup P,Q∈(ΔVj) {|PQ|} — j диаметр части (ΔVj), λ= max{dj} — ранг разбиения, ΔVj— объем части (ΔVj). В каждой частичной области (ΔVj) возьмем произ- вольную точку xj(x1j,x2j,...,xNj) и составим сумму N Σ j=1 f(xj)ΔVj, где ΔVj— объем частичной области (ΔVj). Будем разбивать (V) на все более и более мелкие части так, чтобы λN−→→∞ 0 . Если существует N Σ lim f(xj)ΔVj , не зависящий λ→0 j=1 ∫ ни от способа разбиения (V) на части, ни от выбора точек xjв каждой из этих частей, то он называется интеграломфункции fпо области интегрирования (V) и обозначается ∫∫ ∫··· (V) f(x) dx или f(x1,x2,...,xn) dx1dx2 ...dxn. (V) ∫∫ ∫ Итак, ··· (V) f(x1,x2,...,xn) dx1dx2 ...dxn= Σ N = lim f(x1j,x2j,...,xnj)ΔVj. λ→0 j=1 Из написанного выше следует, что свойства n-кратного инте- грала аналогичны свойствам двойного, тройного интегралов. При вычислении n-кратный интеграл сводится к повторному так же, как двойной, тройной интегралы. Так, например, если 1 1 (V) = {x(x1,x2,...,xn)| x0 ≤ x1 ≤ x′ ,g1(x1) ≤ x2 ≤ h1(x1), g2(x1,x2) ≤ x3 ≤ h2(x1,x2),...,gn−1(x1,x2,...,xn−1) ≤ ≤ xn≤ hn−1(x1,x2,...,xn−1), 1 1 x0 ∈ R,x′ ∈ R,g1,g2,...,gn−1,h1,h2,...,hn−1 ∫∫ ∫ — непрерывные функции, задающие границу (V )}, то ··· (V) f(x1,x2,...,xn) dx1dx2 ...dxn= x'1 h1(x1) h2 (x1,x2) hn−1(x1,x2,...,xn−1) = ∫ dx1 ∫ dx2 ∫ dx3··· ∫ f(x1,x2,...,xn)dxn. 1 x 0 g1 (x1) g2 (x1,x2) gn−1 (x1,x2,...,xn−1) ∫∫ ∫··· Пример. Найти (x1 + 2xn) dx1dx2 ...dxn, если (V) = (V) { | } x(x1,x2,...,xn) 0 ≤ xj≤ 1, j= 1,2,...,n . Решение. ∫∫ ∫ ··· (x1 + 2xn) dx1dx2 ...dxn= (V) ∫ 1 = dx1 0 1 1 ∫ ∫ dx2··· 0 0 dxn−1 1 ∫ (x1 + 2xn)dxn= 0 ∫1 ∫1 ∫1 2 .1 = dx1 dx2··· ∫ 0 0 0 (x1xn+ xn).0dxn−1 = ∫ 1 = (x1 + 1)dx1 x 0 1 1 dx2··· .0 2 0 0 dxn−1 = ∫ 2 = 1 + x1 2 .11 · 1 · ...· 1 = 1 3 +1 = . 2 |
