Пономаренко-Математика. Кратные интегралы. Учебное пособие предисловие данное учебное пособие предназначено для студентов немате

• Название: Учебное пособие предисловие данное учебное пособие предназначено для студентов немате
• Дата: 27.03.2023
• Размер: 0.93 Mb.
• Имя файла: Пономаренко-Математика. Кратные интегралы.docx
• Тип: Учебное пособие; #1019168
• страница: 12 из 17

Сферические координаты

Как и ранее, в пространстве R³ введем прямоугольную декарто- ву систему координат Oxyz. Возьмем прозвольную точку M (x, y, z). Ее сферические координаты ρ, θ, ϕ определяются следующим обра- зом: ρ есть раcстояние точки Mот начала координат — точки O, θ — угол между осью OM и осью Oz, ϕ — угол между полуплоскостью, исходящей из оси Oz и проходящей через точку M , и плоскостью Oxz(рис. 31); 0 ≤ ρ <+∞, 0 ≤ θ≤ π, 0 ≤ ϕ <2π.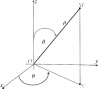




Рис.31


⎧_⎪⎨
Связь с прямоугольными декартовыми координатами:

⎪_⎩
x = ρsin θcos ϕ,y = ρ sin θ sin ϕ,z= ρcos θ.

Координатные поверхности:

1. 
   ρ= const, x² + y² + z² = ρ² — сфера радиуса ρc центром в точке O;
   
2. 
   θ= const, x² + y² = z² tg² θ — прямой круговой конус, ось конуса — ось Oz, вершина — точка O;
   
3. 
   ϕ= const — полуплоскость, исходящая из оси Ozи проходя- щая через точку M.
   

Координатные линии:

1. 
   ^{θ= const,}— координатная линия ρ(полуось, исходящая из
   

ϕ= const



начала координат Oи проходящая через точку M);

2. 
   ^{ρ= const,}— координатная линия θ(полуокружность ради-
   

ϕ= const



уса ρс центром в точке O), проходящая через точку M, концы полуокружности находятся на оси Oz);

3. 
   ^{ρ= const,}— координатная линия ϕ(окружность с центром
   

θ = const

на оси Oz, проходящая через точку M, плоскость, в которой распо- ложена окружность, параллельна плоскости Oxy) (рис. 32).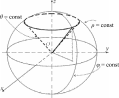





Рис.32

Якобиан преобразования:

∂x ∂ρ ∂y		∂x ∂θ ∂y		∂x ∂ϕ ∂y
∂ρ ∂z		∂θ ∂z		∂ϕ ∂z
∂ρ		∂θ		∂ϕ

. . <sub>. .

. . .</sub>sin θcos ϕρcos θcos ϕ −ρsin θsin ϕ_.

J(ρ,θ,ϕ)=

.

= sin θsin ϕ ρcos θsin ϕ ρsin θcos ϕ =

^. . .

cos θ −ρsin θ0

. .


_{=cos θ.}ρcos θcos ϕ−ρsin θsin ϕ_{.+ρsin θ.}sin θcos ϕ −ρsin θsin ϕ_{. =}
^.ρcos θsin ϕ ρsin θcos ϕ^{. .}sin θsin ϕ ρsin θcos ϕ^.
= ρ² sin θ(cos² θ+ sin² θ) ^{cos ϕ − sin ϕ} = ρ² sin θ.

^.sin ϕ cos ϕ^.

Элемент объема dxdydz= ρ² sin θdρdθdϕ.

Формула (11) принимает вид

∫∫∫
(V)

f(x,y,z) dxdydz=

∫∫∫
=

(ν)

f(ρsin θcos ϕ,ρsin θsin ϕ,ρcos θ) ρ² sin θdρdθdϕ. (14)

Пример. Найти объем тела, ограниченного поверхностью, за- данной уравнением (x² + y² + z²)² = z.


√
Решение. Установим вначале вид заданной поверхности. Это по- верхность вращения вокруг оси Oz кривой с уравнением (x²+z²)² = z, расположенной в плоскости Oxz. Чтобы выяснить ее форму, пе- рейдем в исходном уравнении к сферическим координатам ρ,θ, ϕ: x = ρ sin θ cos ϕ, y= ρ sin θ sin ϕ, z= ρ cos θ. Получим ρ = ³ cos θ.Простые исследования при y= 0 приводят к кривой на рис. 33. Исходная поверхность изображена на рис. 34.


∫∫∫
Обозначим (V ) тело, ограниченное данной поверхностью. Иско- мый объем Vвыражается интегралом dxdydz. Вычислим его,

(V)

перейдя к сферическим координатам ρ, θ, ϕ. Пределы интегриро-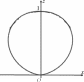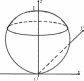

Рис.33 Рис.34

∫
вания расставим в соответствии с рис. 34:

∫∫∫

∫

∫
2π <sup>π/2

√3</sup> cos θ

V=

(V)

dxdydz= dϕ

0 0

sin θdθ

0

ρ²dρ=

∫
2π

= dϕ

π/2


∫
sin θ·

^√3 cos θ


.
_ρ3

₃ .
1

dθ= ₃ · 2π

π/2


∫
sin θcos θdθ=

0

0 0


∫
π/2

2
2 sin²

0


.
π/2

θ1

= π sin θd(sin θ) = π

3 3

0

₂ .₀

= π.

3

Задание. Из задачника [4] решить примеры № 3552–3558, 3615– 3617, 3619, 3623.