Пономаренко-Математика. Кратные интегралы. Учебное пособие предисловие данное учебное пособие предназначено для студентов немате
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
Цилиндрические координатыПусть в пространстве R3 введена прямоугольная декартова си- стема координат Oxyz. Возьмем прозвольную точку M (x, y, z). Ее цилиндрические координаты r, ϕ, z определяются следующим обра- зом: полярный радиус r есть растояние точки M от оси Oz, поляр-ный угол ϕ — угол между полуплоскостью, исходящей из оси Oz и проходящей через точку M, и плоскостью Oxz, z — аппликата точки M(рис. 28); 0 ≤ r<+∞, 0 ≤ ϕ<2π, −∞ <z< +∞. 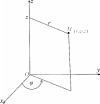 Рис.28 ⎧⎪⎨ Связь с прямоугольными декартовыми координатами: ⎪⎩ x = r cos ϕ,y = r sin ϕ,z= z. Координатные поверхности: r= const, x2 + y2 = r2 — прямой круговой цилиндр с осью, совпадающей с осью Oz, образующими, паралельными этой оси, радиус цилиндра равен r; ϕ= const — полуплоскость, исходящая из оси Ozи проходя- щая через точку M; z= const — плоскость, параллельная плоскости Oxyи прохо- дящая через точку M. Координатные линии: ϕ= const,— координатная линия r(полуось, исходящая из z= const оси Oz, проходящая через точку Mи параллельная плоскости Oxy); r= const, — координатная линия ϕ(окружность радиуса rz= const с центром (0, 0, z), проходящая через точку M); r= const,— координатная линия z (прямая, параллельная ϕ= const оси Ozи проходящая через точку M) (рис. 29). 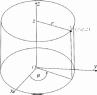 Рис.29 Найдем якобиан преобразования: ∂x∂x∂x . . ∂r ∂y ∂ϕ ∂y ∂z ∂y .cos ϕ −rsin ϕ 0. . . . . J(r,ϕ,z) = . ∂r = sin ϕrcos ϕ0 = r. ∂ϕ ∂z. . 0 0 1. ∂z . ∂r ∂z∂z ∂ϕ ∂z. ∫∫∫ ∫∫∫ Формула (11) запишется в виде (V) f(x,y,z) dxdydz= (ν) f(rcos ϕ,rsin ϕ,z)rdrdϕdz. (13) ∫∫∫ Пример. Вычислить интеграл I= xdxdydz, если область (V) интегрирования (V) ограничена поверхностями x2 + y2 = 2x, x2 + y2 = z2, z= 0 (та часть цилиндра, где 0 ≤ z, рис. 30). 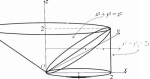 Рис.30 Решение. Перейдем к цилиндрическим координатам. Уравнение цилиндра x2 + y2 = 2xпримет вид r = 2 cos ϕ, а уравнение конуса x2 + y2 = z2 станет r= z. Чтобы найти пределы интегрирования по z , решим систему уравнений x2 + y2 = 2x x2 + y2 = z2 при условии 0 ≤ x≤ 2. Отсюда 0 ≤ z≤ 2. Пределы интегрирования по ϕ и r ясны из рис. 30. Далее, элемент объема dxdydz= rdrdϕdz. Исходный интеграл запишется в виде I = ∫∫∫ 2 2 π ∫ ∫ xdxdydz= dz 2 cos ϕ ∫ dϕrcos ϕ· rdr= (V) π .cos ϕr dϕ= 1 ∫2 ∫2 . 0 − 2 z π 1 ∫2 ∫2 0 − = dz 3 π 2 r=2 cos ϕ r=z ∫ ∫ π dz cos ϕ 3 π 2 ∫ ∫ π 8 cos3 ϕ−z3 dϕ= 2 2 8 = dz − 0 3 2 2 1 − cos4 ϕdϕ dz − 0 3 z3 cos ϕdϕ. π π 2 2 π 8 ∫2 cos4 ϕdϕ= 16 ∫2 (1+ cos 2ϕ)2 0 dϕ= π − 3 3 4 π 2 π 4 ∫2 1+cos4ϕ 4 3 π = 1+2 cos 2ϕ+ 3 2 0 dϕ= 3 · 2 · 2 +0 = π. ∫ π z3 2 — 3 − π 2 cos ϕdϕ= − π ∫ 2z3 2 3 0 cos ϕdϕ= − 2z3 3 sin ϕ.π/2 = − 2z3 . 3 0 2 ∫2 . π− 3 z dz= πz− 3 · . = 2π− 3 = 3 (3π− 4). z . I= 2 3 2 4 8 2 |
