Урок 1 Числовые выражения
 Скачать 2.02 Mb. Скачать 2.02 Mb.
|
|
V. Итоги урока. – Что называется графиком функции? – Как построить график функции, заданной формулой? – Как по графику найти значение функции, соответствующее данному значению аргумента? – Как по графику функции найти значение аргумента, которому соответствует данное значение функции? – Как по графику зависимости определить, является ли она функцией? Домашнее задание: 1. № 286; № 287; № 288. Урок 29 График функции Цели: продолжить формировать умения строить график функции и находить значение функции по заданному аргументу с помощью графика; формировать умение интерпретировать в несложных случаях графики реальных зависимостей между величинами, отвечая на поставленные вопросы практической задачи. Ход урока I. Организационный момент Устная работа. 1. Какие из графиков, изображенных на рисунках, являются графиками функций? а) 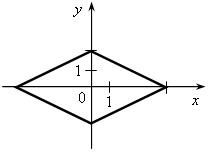 б) б) 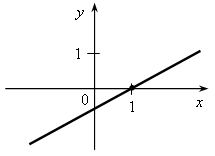 в) в) 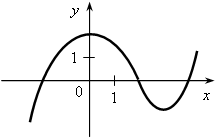 г) г) 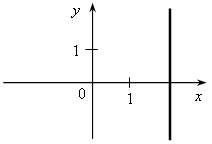 д) 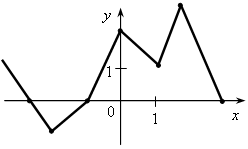 е) е) 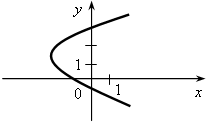 2. По графику, изображенному на рисунке д), найдите: а) значение функции, соответствующее значению аргумента, равному –3; –2; 1; 2; б) значения аргумента, при которых значение функции равно –1; 2; 3; в) координаты точек пересечения с осью х; г) координаты точек пересечения с осью у. II. Формирование умений и навыков. 1. № 289. 2. № 291, № 293. 3. На рисунке изображен график зависимости потребления районом электрической энергии р (%) от времени суток t (ч). 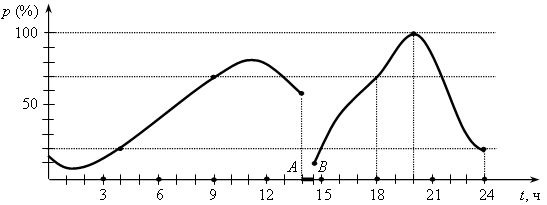 а) В какое время суток электрическая нагрузка была максимальной? б) В какое время суток нагрузка не превосходила 20 % от максимума? в) Какова была нагрузка в 18 ч? г) Какое событие может отражать участок графика АВ? д) Возрастала или убывала нагрузка с 4 до 8 ч; с 18 до 20 ч? 4. В таблице представлено население (млрд) земного шара в различные годы.
По этим данным постройте график. Оцените приближенно по графику население земли в 1981, 1987, 2010 гг. 5. (Криминальная история.) В 11 ч вечера слуга зажег хозяину две свечи, а утром в 7 ч обнаружил его убитым. Одна свеча лежала на полу потухшая, а вторая догорала. В какое время произошло убийство, если длина целой свечи 21 см, опрокинутой во время убийства 16 см, а непотухшего огарка 1 см? Постройте график зависимости длины горения свечи от времени. III. Итоги урока. – Как по графику найти значение функции, соответствующее данному значению аргумента? – Как по графику найти значения аргумента, которым соответствует данное значение функции? – Как, не строя график, выявить принадлежность ему точки с данными координатами? – Как, не строя график, определить, в каких точках он пересекает ось абсцисс; ось ординат? Домашнее задание: № 290; № 292; № 355; № 356*. Урок 33 прямая пропорциональность Цели: ввести понятие прямой пропорциональности как функции определенного вида; формировать умение распознавать прямую пропорциональность и вычислять значение функции по формуле; повторить тему «Построение точек в координатной плоскости» для последующего изучения графика прямой пропорциональности. Ход урока I. Устная работа. 1. Найдите значение функции у = а) 0; б) 4; в) –4; г) –2. 2. Проверьте, принадлежат ли графику функции, заданной формулой у = 2х + 14, следующие точки: а) А (0; 14); б) В (–2; 8); в) С (–7; 0); г) D (7; 0). 3. Решите уравнение. а) 3х = 12; б) –2х + 14 = 0; в) х – 15 = 2; г) х + 2 = х. II. Объяснение нового материала. 1. Введение понятия основывается на рассмотрении конкретных практических примеров. Желательно их привести несколько. Так, следует рассмотреть пример со с. 65 учебника. Кроме того, представить уже знакомую учащимся задачу: «Вычислить площадь прямоугольника, основание которого равно 3, а высота равна х». Если искомую площадь обозначить буквой у, то ответ можно записать формулой: у = 3х. Если основание прямоугольника равно k, то зависимость между высотой х и площадью у выразится формулой у = kх. Каждое заданное значение числа k определяет некоторую функцию у = kх. Затем формулируем четкое определение:
2. Просим учащихся привести примеры прямой пропорциональности и примеры функций, не являющихся прямой пропорциональностью. Также рассматриваем примеры со с. 66 учебника. Показываем, что число k называется коэффициентом прямой пропорциональности, а само название функции связано со следующей пропорцией: у = kх.  III. Формирование умений и навыков. Задания, решаемые на этом уроке, можно разбить на 2 блока. В первом блоке представлены упражнения на усвоение понятия прямой пропорциональности и выполнение основных действий по формуле. Второй блок носит повторительный характер и направлен на актуализацию знаний по теме «Построение точек в координатной плоскости». 1-й блок 1. № 297, № 298 (устно). 2. Книга стоит 150 рублей. Выразите формулой зависимость между купленным количеством (п) данных книг и уплаченной суммой (у) в рублях. 3. Автомобиль «Лада» движется по шоссе со скоростью 80 км/ч. Записать формулу, выражающую зависимость длины пути s (в км) от времени движения t (в ч). Чему равно s (3), s (5,4)? 4. Зависимость между переменными х и у выражена формулой у = kх. Определить k, если у = –5 при х = 2,5. 5. Дана таблица значений функции у = kх:
Найти k и заполнить пропущенные клетки. 2-й блок Самостоятельная работа Вариант 1 1. Постройте систему координат. Отметьте в координатной плоскости точки: (2,5; 1), (2,5; –1), (0,4; 3,5), (–0,4; 3,5). 2. Запишите координаты точек: 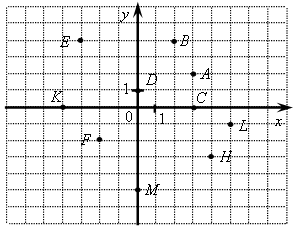 3. В каких координатных четвертях расположены точки: А (–87; 98); В (0,1; –0,01); С (–1,25; –3,48)? 4. Постройте в координатной плоскости прямую проходящую через точки С (–4; 3) и D (3; –1). Найдите координаты точек, в которых эта прямая пересекает ось х и ось у. Вариант 2 1. Постройте систему координат. Отметьте в координатной плоскости точки: (4; 3,5), (4; –3,5), (–5,3; –1,5), (5,3; –1,5). 2. Запишите координаты точек: 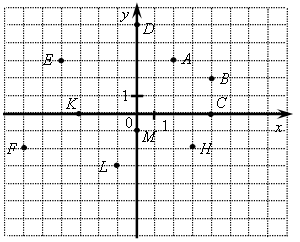 3. В каких координатных четвертях расположены точки: А (25; 360); В (–2,5; –100); С  ? ?4. Постройте в координатной плоскости прямую, проходящую через точки А (3; 4) и В (–5; –1). Найдите координаты точек, в которых эта прямая пересекает ось х и ось у. IV. Итоги урока. – Сформулируйте определение прямой пропорциональности. – Приведите примеры прямой пропорциональности. – Как называется число k в записи формулы прямой пропорциональности у = kх? Какое это число? – Почему данная функция получила свое название? Домашнее задание: 1. № 299. . № 310; № 311. Вариант 1 1. Постройте систему координат. Отметьте в координатной плоскости точки: (2,5; 1), (2,5; –1), (0,4; 3,5), (–0,4; 3,5). 2. Запишите координаты точек:  3. В каких координатных четвертях расположены точки: А (–87; 98); В (0,1; –0,01); С (–1,25; –3,48)? 4. Постройте график функции y=-3x+5 Вариант 2 1. Постройте систему координат. Отметьте в координатной плоскости точки: (4; 3,5), (4; –3,5), (–5,3; –1,5), (5,3; –1,5). 2. Запишите координаты точек:  3. В каких координатных четвертях расположены точки: А (25; 360); В (–2,5; –100); С 4 Постройте график функции y= 2x - 7 Вариант 1 1. Постройте систему координат. Отметьте в координатной плоскости точки: (2,5; 1), (2,5; –1), (0,4; 3,5), (–0,4; 3,5). 2. Запишите координаты точек:  3. В каких координатных четвертях расположены точки: А (–87; 98); В (0,1; –0,01); С (–1,25; –3,48)? 4. Постройте график функции y=-3x+5 Вариант 2 1. Постройте систему координат. Отметьте в координатной плоскости точки: (4; 3,5), (4; –3,5), (–5,3; –1,5), (5,3; –1,5). 2. Запишите координаты точек:  3. В каких координатных четвертях расположены точки: А (25; 360); В (–2,5; –100); С 4. Постройте график функции y= 2x - 7 Вариант 1 1. Постройте систему координат. Отметьте в координатной плоскости точки: (2,5; 1), (2,5; –1), (0,4; 3,5), (–0,4; 3,5). 2. Запишите координаты точек:  3. В каких координатных четвертях расположены точки: А (–87; 98); В (0,1; –0,01); С (–1,25; –3,48)? 4. Постройте график функции y=-3x+5 Вариант 2 1. Постройте систему координат. Отметьте в координатной плоскости точки: (4; 3,5), (4; –3,5), (–5,3; –1,5), (5,3; –1,5). 2. Запишите координаты точек:  3. В каких координатных четвертях расположены точки: А (25; 360); В (–2,5; –100); С 4 Постройте график функции y= 2x - 7 Урок 34 График прямой пропорциональности Цели: определить график прямой пропорциональности как прямую, проходящую через начало координат; выявить расположение прямой в зависимости от знака коэффициента пропорциональности; формировать умение строить график прямой пропорциональности по формуле и выполнять обратное действие – записывать по графику формулу функции. Ход урока I. Устная работа. 1. Найдите область определения функции. а) y = 3x + 2; б) y =  ;г) y = ;г) y = 2. Является ли функция прямой пропорциональностью: а) y = 182x;б) y = 3. Функция задана формулой у = kх. Найдите коэффициент прямой пропорциональности k, если: а) х = 2; у = 4; б) x = II. Объяснение нового материала. Начинаем с рассмотрения конкретной функции (см. учебник, с. 66). Можно предложить учащимся лабораторную работу: подобрать функции, заданные формулами: у = 0,5х; у = –0,5х; у = х; у = –х; у = 1,5х; у = –1,5х; у = 2х; у = –2х; у = 2,5х; у = –2,5х; у = 3х; у = –3х; у = 3,5х; у = –3,5х; у = 4х; у = –4х. Затем заполнить таблицу значений функции при –4 ≤ х ≤ 4 с шагом 0,5. выводы: 1) График прямой пропорциональности является прямой, проходящей через начало координат. 2) Если коэффициент пропорциональности k > 0, то график расположен в первой и третьей координатных четвертях. 3) Если коэффициент пропорциональности k < 0, то график расположен во второй и четвертой координатных четвертях. На основе этих выводов учащиеся выводят простейший алгоритм построения графика прямой пропорциональности: 1-й шаг. Для х1 0 вычислить у1 по формуле у = kх. 2-й шаг. Отметить в координатной плоскости точки с координатами (0; 0) и (х1; у1). 3-й шаг. Провести прямую через построенные точки. |
